Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 28. Криволинейные интегралы 1 и 2 рода, их основные свойства и их
Содержание
- 1. Лекция 28. Криволинейные интегралы 1 и 2 рода, их основные свойства и их
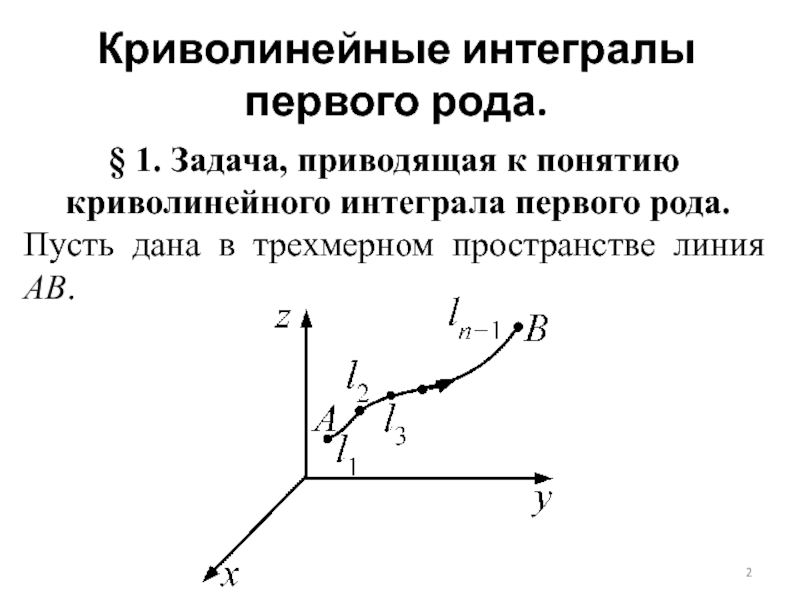
- 2. Криволинейные интегралы первого рода.§ 1. Задача, приводящая
- 3. Дуга АВ такая, что:Гладкая (т.е. в любой
- 4. Найдем значение линейной плотности материала в каждой
- 5. Но масса это физическая величина и не
- 6. Определение (Криволинейного интеграла
- 7. Теорема существования и свойства криволинейного интеграла 1
- 8. Свойства криволинейных интегралов 1-го рода Считаем,
- 9. 4. Свойство аддитивности относительно участка
- 10. 7. Если даны функции f
- 11. § 2. Вычисление криволинейного интеграла первого рода.Теорема
- 12. Доказательство.Самостоятельно.§ 3. Применение криволинейных интегралов
- 13. 3. Для вычисления координат центра тяжестиm – масса всей дуги
- 14. 4. Для вычисления момента инерции относительно оси
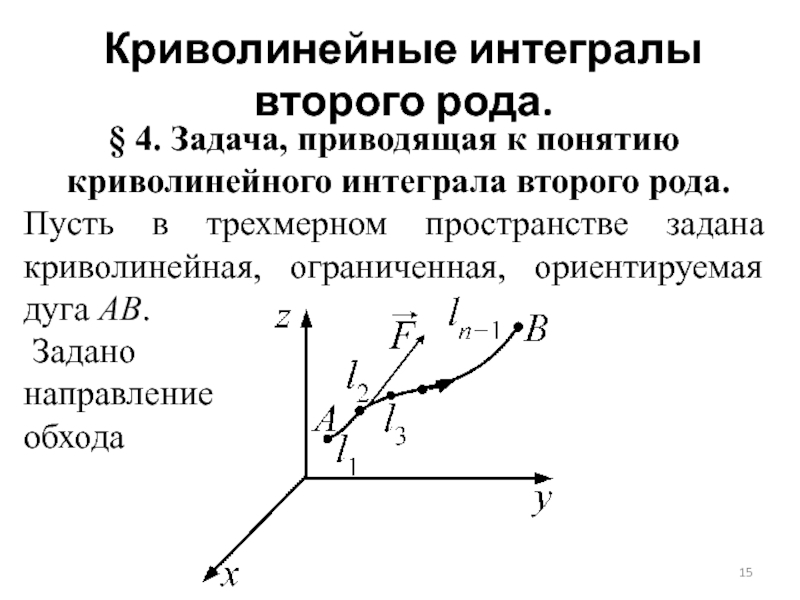
- 15. Криволинейные интегралы второго рода.§ 4. Задача, приводящая
- 16. Пусть по дуге АВ от А к
- 17. Слайд 17
- 18. = Fx(Pi)xi + Fy(Pi)yi
- 19. Поэтому, чтобы работа не зависела от способа
- 20. I - Fx(Pi)xi + Fy(Pi)yi
- 21. Свойства криволинейных интегралов 2-го рода Свойства
- 22. 2. Если участок интегрирования АВ
- 23. § 5. Вычисление криволинейного интеграла второго рода.Криволинейный
- 24. АВ:
- 25. Вынося dt за общую скобку, получаем формулу для вычисления криволинейного интеграла второго рода:Доказательство.Самостоятельно.
- 26. Таким образом, чтобы вычислить криволинейный интеграл 2-го
- 27. § 6. Связь криволинейных интегралов второго рода
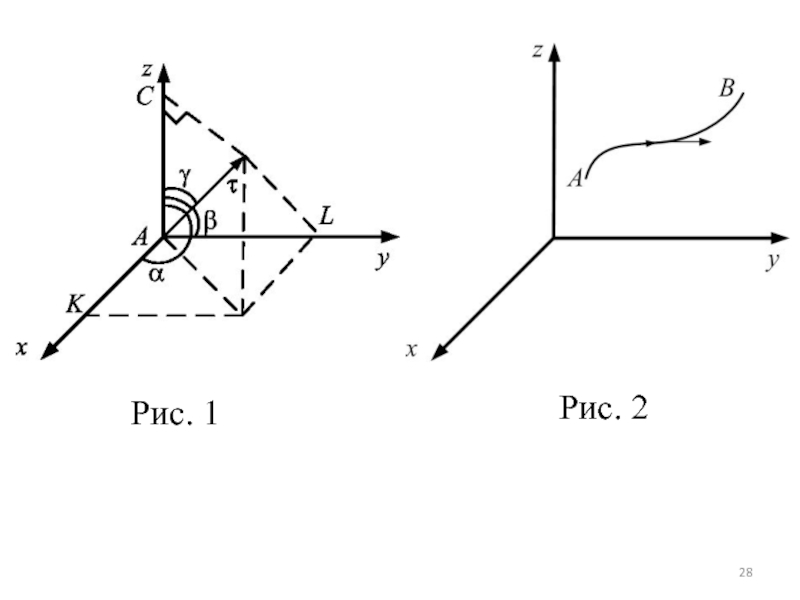
- 28. Рис. 1Рис. 2
- 29. касательной, направленный в сторону обхода дуги).dx =
- 30. дает связь между криволинейными интегралами 1-го и
- 31. криволинейный интеграл 1-го рода ошибки не допустим.Если
- 32. Если дуга задана в виде:АВ:
- 33. § 7. Формула Грина. Формула связывает
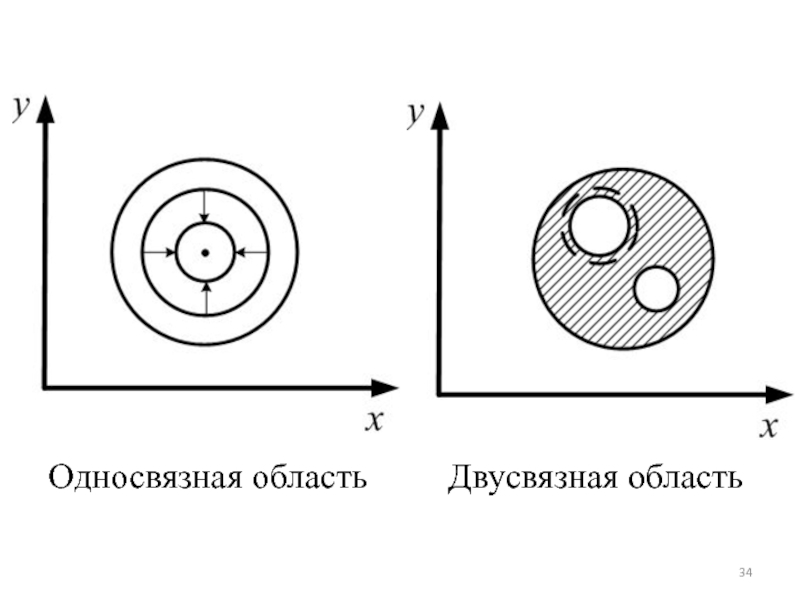
- 34. Односвязная область Двусвязная область
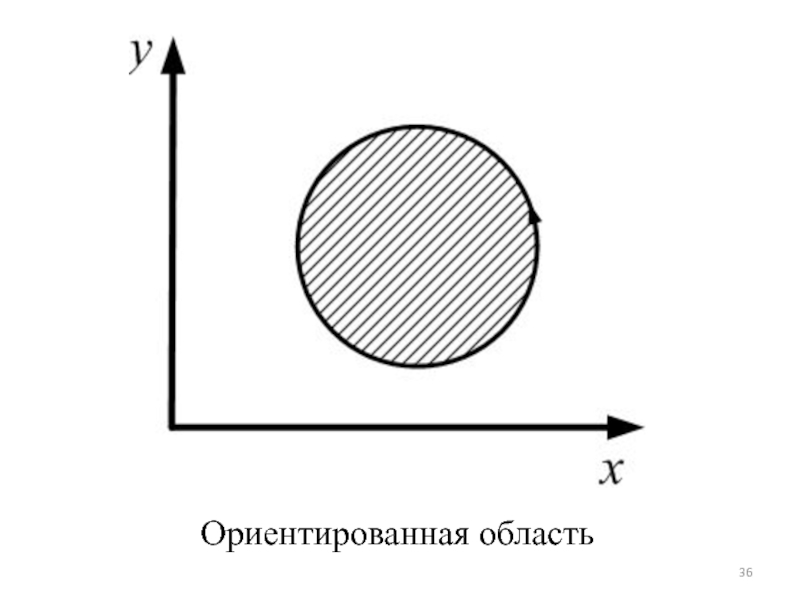
- 35. Определение (ориентированной области). Область D на
- 36. Ориентированная область
- 37. Формула Грина. Если любую область с помощью
- 38. Слайд 38
- 39. интегрирования, а зависел от положения начальной и
- 40. Скачать презентанцию
Криволинейные интегралы первого рода.§ 1. Задача, приводящая к понятию криволинейного интеграла первого рода.Пусть дана в трехмерном пространстве линия АВ.
Слайды и текст этой презентации
Слайд 2Криволинейные интегралы первого рода.
§ 1. Задача, приводящая к понятию
криволинейного
интеграла первого рода.
Пусть дана в трехмерном пространстве линия АВ.
Слайд 3Дуга АВ такая, что:
Гладкая (т.е. в любой точке существует касательная);
Спрямляемая
(т.е. имеющую длину).
Пусть в любой точке дуги задана линейная плотность
материала, из которой может быть изготовлена дуга АВ. Найти массу дуги АВ.Разобьем дугу АВ точками: l1’ l2’… ln+1. Между 2-мя соседними точками лежат элементарные участки дуги АВ.
Dli=li+1–li, i=1,2,…n+1. Выберем на каждом участке точки Р1 , Р2 ,… Рn , Рi = Рi (x,y,z).
Слайд 4Найдем значение линейной плотности материала в каждой из этих точек.
Умножим
длину элементарного участка дуги на элементарную плотность.
m(P1)Dl1, m(P2)Dl2… Это
масса каждого элементарного участка, при условии, что плотность на участке считается постоянной..
Если просуммировать, то получим приближенное значение массы. Значение массы зависит от разбиения и от выбора точкиPi .
Слайд 5Но масса это физическая величина и не зависит от способа
разбиения и выбора точек Pi. Надо ввести характеристику не зависящую
от этих величин. Назовем сумму- интегральной суммой.
Определение (предела интегральной суммы): Число I называется пределом интегральной суммы
если для всех e 0 существует e (не зависящая от способа разбиения и выбора точек Pi, такая, что из неравенства
Слайд 6
Определение (Криволинейного интеграла 1-го рода). Если
существует предел интегральной суммы I, то он называется криволинейным интегралом
1-го рода. При этом пишут:Физическое значение интеграла 1 рода - масса дуги АВ.
Слайд 7Теорема существования и свойства криволинейного интеграла 1 рода.
Теорема (достаточные условия
существования): Если функция (х,у,z) непрерывна в каждой точке дуги АВ,
то криволинейный интегралсуществует.
Теорема (необходимые условия существования): Если существует криволинейный интеграл , то
(х,у,z) ограничена на дуге АВ.
Слайд 8Свойства криволинейных интегралов 1-го рода
Считаем, что все
интегралы существуют.
1. Криволинейный интеграл не зависит от направления обхода
дуги АВ.2. Обладает свойством однородности:
, с = const.
3. Свойство аддитивности относительно подынтегральной функции:
Слайд 9 4. Свойство аддитивности относительно участка интегрирования:
то
5. Если f (x,y,z) 1 на дуге АВ, то
= LAB – длина дуги.
6. Если f (x,y,z) > 0 на дуге АВ и непрерывны, то
При этом все интегралы .
Слайд 10 7. Если даны функции f (x,y,z) и (x,y,z)
на дуге АВ удовлетворяет неравенству f > , то интеграл
на AB:8. Теорема о среднем для криволинейных интегралов 1-го рода.
Если f (x,y,z) непрерывна на замкнутой (с присоединенными концами), ограниченной дуги АВ, то существует такая точка АВ, что
Слайд 11§ 2. Вычисление криволинейного интеграла первого рода.
Теорема (о вычисление криволинейного
интеграла первого рода). Если f (х,y,z) непрерывна на дуге
AB, которая может быть задана параметрически формуламиАВ: , где:
1. t [; ]
2. x(t), y(t), z(t) монотонны и непрерывно дифференцируемы на [; ].
3. (xt)2 + (yt)2 + (zt)2 0 на [; ], тогда:
Слайд 12
Доказательство.
Самостоятельно.
§ 3. Применение криволинейных интегралов первого рода.
1. Масса
дуги
где: (x,y,z) – линейная плотность материала.
2. Для
вычисления длины дугиСлайд 15Криволинейные интегралы второго рода.
§ 4. Задача, приводящая к понятию
криволинейного
интеграла второго рода.
Пусть в трехмерном пространстве задана криволинейная, ограниченная, ориентируемая
дуга АВ.Задано
направление
обхода
Слайд 16Пусть по дуге АВ от А к В движется материальная
точка под действием силы .
Найти работу силы при
движении материальной точки по дуге АВ.Разобьем дугу АВ точками: l1’ l2’… ln+1. На каждом из отрезков выберем точки Р1 , Р2 ,… Рn .
Рассмотрим элементарную дугу, заключенную между точками li и li+1.
Пусть в точке Pi есть векторы касательной
и силы .
Если считать, что в каждой точке дуги материальная точка движется не по кривой, а по прямой, то элементарная работа силы равна:
Слайд 17
= Fx(Pi)xi + Fy(Pi)yi + Fz(Pi)zi
перемещение
Зная элементарную работу на
каждом участке li для всей работы силы на дуге АВ, можем записать приближенное выражениеСлайд 18
= Fx(Pi)xi + Fy(Pi)yi + Fz(Pi)zi
- вектор,
который направлен по касательной.
Сумма, стоящая в правой части выражения называется
интегральной суммой. При этом, еслитак как
то: xi 0, yi 0, zi 0.
Слайд 19Поэтому, чтобы работа не зависела от способа разбиения дуги точками
li и выбора точек Pi . Введем понятие криволинейного интеграла
2-го рода как предела интегральной суммы при .Определение (предела интегральной суммы) Число I называется пределом интегральной суммы, если для > 0 > 0, не зависящее от способа разбиения и выбора точек Pi, такое что из неравенства
следует неравенство:
Слайд 20I - Fx(Pi)xi + Fy(Pi)yi + Fz(Pi)zi
<
При этом число I называется криволинейным интегралом 2-го рода
и обозначают:или
При этом из задачи, приводящей к криволинейному интегралу 2-го рода видно, что для этих интегралов существенно то, что дуга АВ ориентирована.
Слайд 21Свойства криволинейных интегралов 2-го рода
Свойства 2-7 такие же
как и для криволинейных интегралов 1-го рода.
Помимо этих свойств они
обладают следующими свойствами.Считаем, что все интегралы существуют.
1. Криволинейный интеграл 2-го рода меняет знак при изменении обхода дуги АВ.
Слайд 22 2. Если участок интегрирования АВ параллелен оси ОХ,
то интеграл по этому участку АВ = 0
АВ OY
Слайд 23§ 5. Вычисление криволинейного интеграла второго рода.
Криволинейный интеграл 2-го рода
можно вычислять если дугу АВ задать параметрически. Причем будем предполагать
выполнимыми все условия, которым удовлетворяло параметрическое задание дуги. Пусть даныи дуга
Слайд 24
АВ:
, где:
1. t [; ]
2. x(t), y(t),
z(t) монотонны и непрерывно дифференцируемы на [; ].3. (xt)2 + (yt)2 + (zt)2 0 на [; ].
Тогда криволинейный интеграл 2-го рода можно вычислять по формуле:
Слайд 25
Вынося dt за общую скобку, получаем формулу для вычисления криволинейного
интеграла второго рода:
Доказательство.
Самостоятельно.
Слайд 26Таким образом, чтобы вычислить криволинейный интеграл 2-го рода необходимо:
1. Задать
дугу АВ параметрически с учетом направления обхода так, чтобы установить
однозначное соответствие между дугой АВ и параметром t.2. Подставить вместо x, y, z соответствующие выражения в формулу и подсчитать определенный интеграл от одной переменной t.
Слайд 27§ 6. Связь криволинейных интегралов второго рода с криволинейными интегралами
первого рода.
Пусть в пространстве есть единичный вектор (рис.
1), который с осями координат составляет углы , , . Это плоские углы. Тогда координатами этого единичного вектора будут числа= (cos, cos, cos)
Пусть в трехмерном пространстве (рис. 2) есть гладкая ориентированная дуга AB (то есть в каждой точке дуги существует вектор
Слайд 29касательной, направленный в сторону обхода дуги).
dx = dlcos
dy = dlcos
dz
= dlcos
Три этих выражения дают значение проекции длины дуги на
оси координат с учетом ориентации дуги. Ориентация дуги учитывается косинусами cos, cos, cos.Подставляя полученные выражения в интеграл 2-го рода, имеем:
Слайд 30
дает связь между криволинейными интегралами 1-го и 2-го рода.
Хотя криволинейные
интегралы первого рода не зависит от направления обхода дуги АВ,
так в формулу входят cos, cos, cos, учитывающих ориентацию дуги АВ, то пользуясь этой формулой и вычисляют криволинейный интеграл 2-го рода черезСлайд 31криволинейный интеграл 1-го рода ошибки не допустим.
Если на плоскости есть
дуга
АВ, которая задается
графиком функции y = f (x).
АВ:
t изменяется от a до b.
Так вычисляется интеграл, если дуга задана параметрически.
Слайд 32Если дуга задана в виде:
АВ:
x изменяется от a до b.
Тогда
Для
криволинейных интегралов 2-го рода нижний предел интегрирования может быть больше верхнего.Слайд 33§ 7. Формула Грина.
Формула связывает криволинейные интегралы по
замкнутому контуру с интегралом по области, границей которой является этот
контур.Определение (односвязной области). Область D на плоскости называется односвязной, если любую замкнутую линию, принадлежащей этой области, можно непрерывной деформацией стянуть в точку.
Слайд 35 Определение (ориентированной области). Область D на плоскости называется ориентированной
односвязной, если:
Она односвязная.
2. Обход границы области происходит так, что область
все время остается слева.Из определения видно, что обход границы осуществляется против часовой стрелки. Такое направление обхода назовем положительным.
Для односвязных ориентированных областей справедлива формула Грина.
Слайд 37Формула Грина. Если любую область с помощью прямых, параллельных осям
X и Y можно разбить на прямоугольные и треугольные области,
причем направление обхода таких областей выбирается против часовой стрелки. Криволинейные интегралы по границам соседних областей, обходимых в противоположном направлении = 0. Поэтому, складывая формулы Грина для каждой из областей разбиения, поле суммирования получим интеграл по границе области D.Слайд 38
- это криволинейный интеграл 2-го рода, который берется
по границе области D при положительном направлении обхода. Он является интегралом по замкнутому контуру.Из формулы Грина следует условие независимости криволинейного интеграла 2-го рода от пути интегрирования.
Теорема (условие независимости). Для того, чтобы криволинейный интеграл 2-го рода не зависел от пути
Слайд 39интегрирования, а зависел от положения начальной и конечной точек дуги
интегрирования необходимо и достаточно, чтобы выполнялось хотя бы одно из
условий:1.
2.
3. Pdx + Qdy – было полным дифференциалом некоторой функции F(x,y).
Все три условия между собой связаны. При выполнении одного из них, все остальные выполняются.