Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 3
Содержание
- 1. Лекция 3
- 2. Почти все материальные
- 3. Свободными или собственными
- 4. 2.3.1. Гармонические колебания
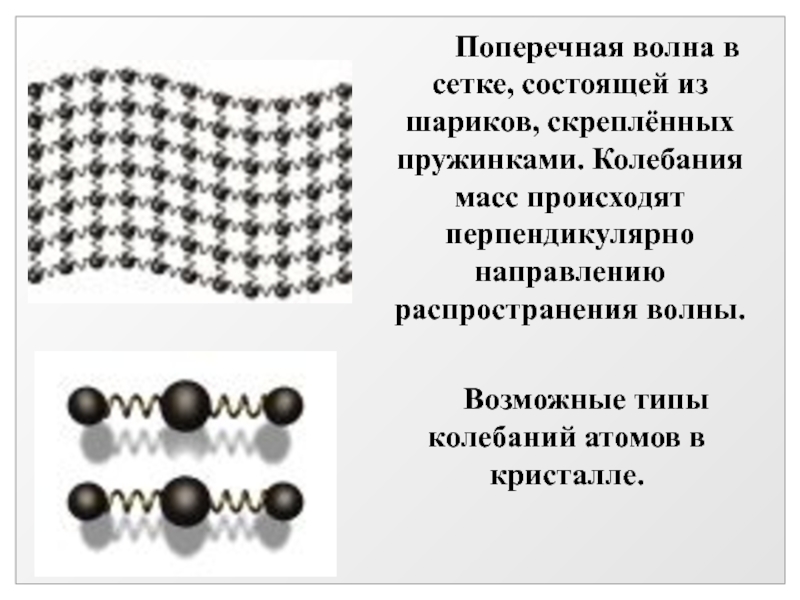
- 5. Поперечная волна в
- 6. Гармоническое колебание
- 7. Величина А называется
- 8. За один оборот колеблющаяся точка вернется
- 9. 2π0π/2πλtЗа период Т фаза меняется от 0 ÷ 2π, а волна проходит путь = λ.3/2πРис. 2
- 10. Слайд 10
- 11. Слайд 11
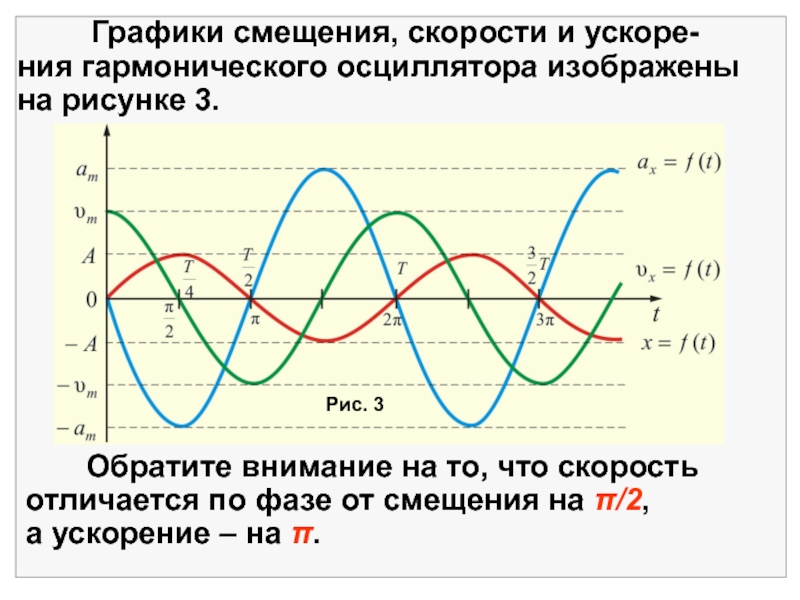
- 12. Рис. 3
- 13. Слайд 13
- 14. Е ~ А2
- 15. Слайд 15
- 16. Пусть тело одновременно
- 17. Ox – опорная прямаяA1, А2 и φ1,
- 18. Результирующее колебание определяется уравнением вида (3 )Из
- 19. 1. Разность фаз равна нулю или четному
- 20. Результирующее колебание2. Разность фаз равна нечетному числу π, то есть колебания в противофазеА1А2Ах0tРис. 6
- 21. 3. Разность фаз изменяется во времени
- 22. Слайд 22
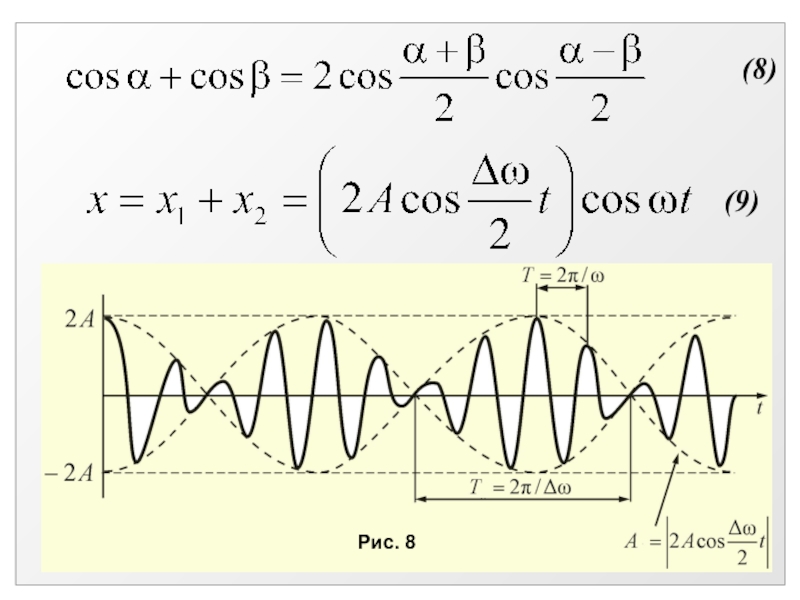
- 23. (8)(9)Рис. 8
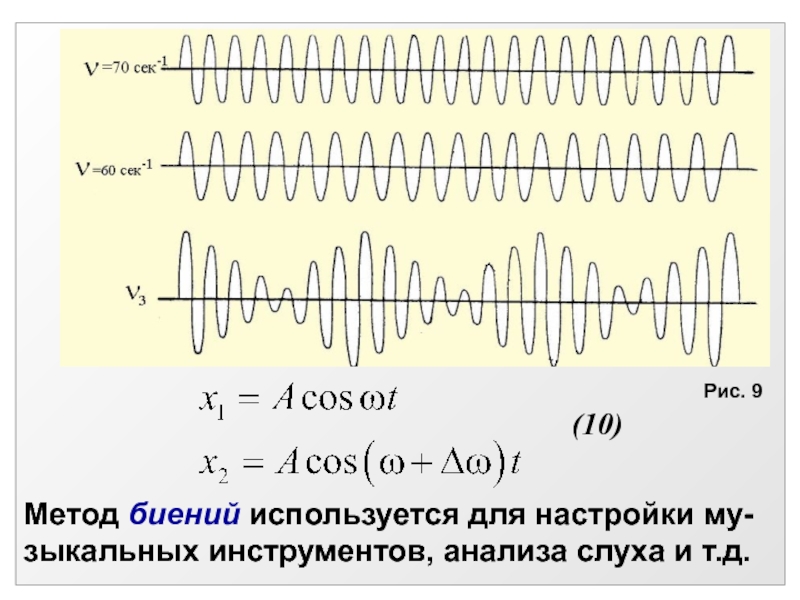
- 24. (10)Метод биений используется для настройки му-зыкальных инструментов, анализа слуха и т.д.Рис. 9
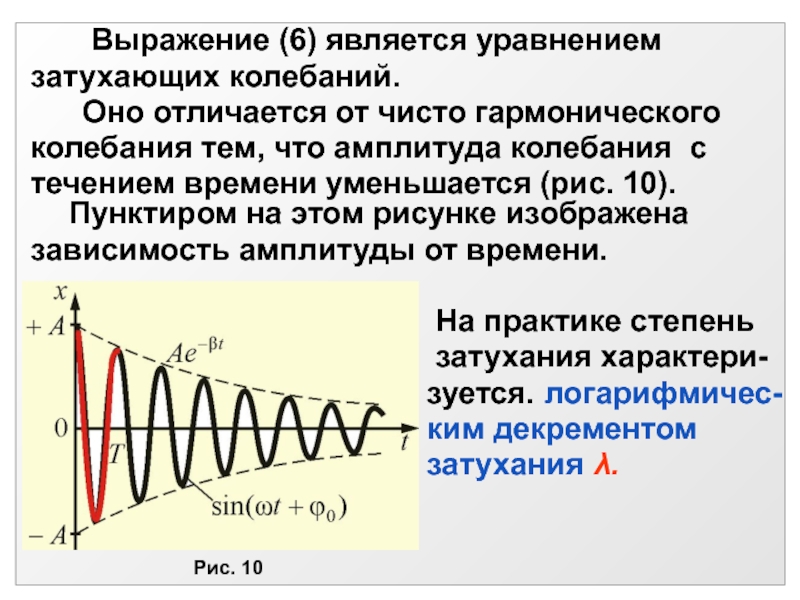
- 25. 2.3.6. Затухающие колебания
- 26. (2)(3)(4)
- 27. .(5)(6)(7)
- 28. Рис. 10
- 29. Слайд 29
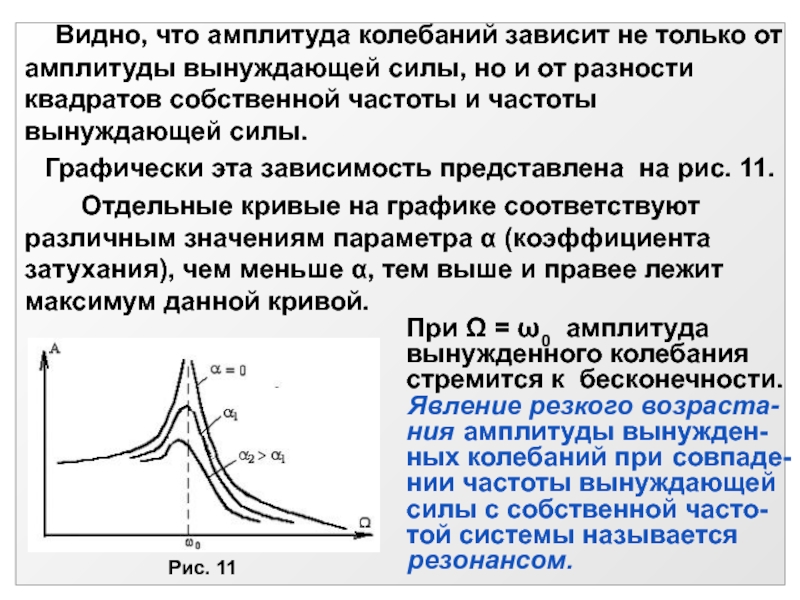
- 30. 2.3.7. Вынужденные колебания Вынужденными
- 31. Слайд 31
- 32. Рис. 11
- 33. Слайд 33
- 34. Слайд 34
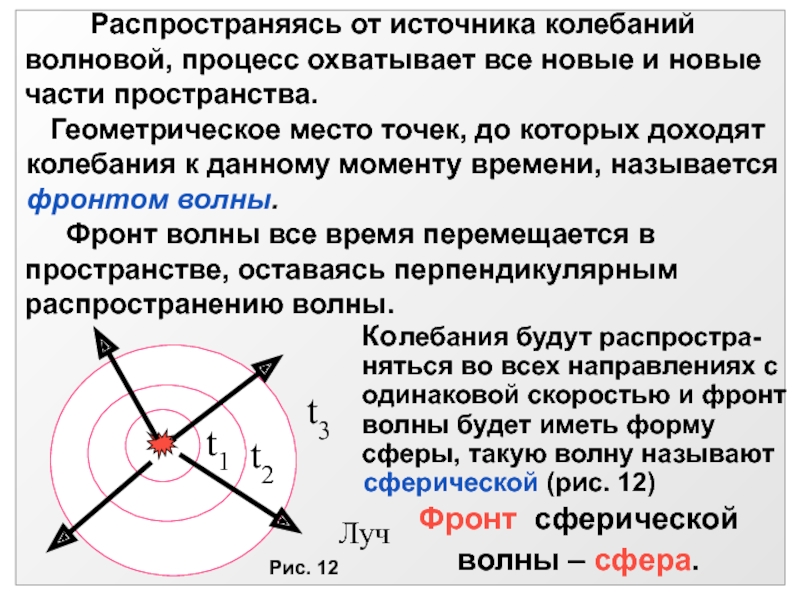
- 35. Фронт сферической волны – сфера. t3t1t2ЛучРис. 12
- 36. Волна называется плоской, если ее
- 37. Расстояние между ближайшими
- 38. 2.3.9. Звук Понятие звука обычно ассоциируется
- 39. Скорость звука в различных веществах
- 40. Опыт показывает, что инфразвуковые волны
- 41. Ультразвуковые волны отличаются от слышимого звука большой
- 42. Спасибо за вниманиеЛекция окончена
- 43. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 3
Курс лекций «Физика для студентов ФармФ»
2. МЕХАНИКА
2.3. Механические колебания
и волны
колебаться, или осциллировать: груз на конце пружины, камертон, колесико балансира в часах, маятник, пластмассовая линейка, крепко прижатая одним концом к краю стола, струны гитары или фортепиано. Пауки обнаруживают попавшую в их сети добычу по дрожанию паутины, корпус автомобиля колеблется вверх-вниз на рессорах, когда автомобиль проезжает неровности, дома и мосты дрожат при проезде тяжелых грузовиков и даже при сильном ветре.Слайд 2 Почти все материальные предметы колеблются (хотя
бы недолго), после того как на них подействует импульс силы.
На атомном уровне атомы колеблются в молекулах, а в твердом теле атомы совершают колебания относительно своих фиксирован-ных положений в решетке.
Колебательное движение имеет огромную важность, поскольку оно широко распростра-нено и встречается во многих разделах физики.
В общем случае колебательными процессами или колебаниями называются процессы, точно или приблизительно повторяющиеся через одинаковые промежутки времени.
Слайд 3 Свободными или собственными называ-ются такие колебания,
которые происходят в системе под действием внутренних сил самой системы,
после того, как эта система была выведена из положения равновесия.Равнодействующую внутреннюю силу, под действием которой происходит колебательный процесс, называют возвращающей силой, т.к. она стремится тело или материальную точку, отклоненную от положения равновесия, вернуть в это положение.
Вынужденными называются колебания, происходящие под действием внешней периодически изменяющейся силы.
Слайд 4 2.3.1. Гармонические колебания
Круговая волна на
поверхности жидкости, возбуждаемая точечным источником (гармонически колеблющимся шариком).
Генерация акустической волны громкоговорителем.Простейшим типом периодических колебаний являются гармонические колебания.
Слайд 5
Поперечная волна в сетке, состоящей
из шариков, скреплённых пружинками. Колебания масс происходят перпендикулярно направлению распространения
волны. Возможные типы колебаний атомов в кристалле.
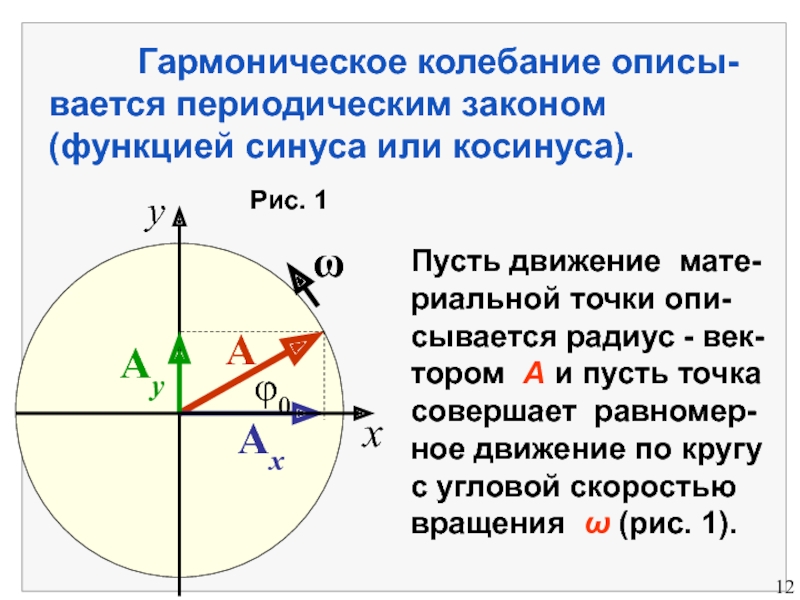
Слайд 6 Гармоническое колебание описы-вается периодическим законом
(функцией синуса или косинуса).
Пусть движение мате-
риальной точки опи-
сывается радиус - век-
тором А и пусть точка
совершает равномер-
ное движение по кругу
с угловой скоростью
вращения (рис. 1).
12
А
х
у
Ах
Ау
φ0
ω
Рис. 1
Слайд 7 Величина А называется амплитудой.
Амплитуда равна абсолютному значению
наибольшего отклонения.
Аргумент синуса или косинуса t + 0 называется фазой колебания,
а 0 = const – начальной фазой (показывает
положение точки в начальный момент времени)
Слайд 8 За один оборот колеблющаяся точка
вернется в свое первоначальное
положение,
а проекция ее радиус-вектора совершит одно
полное колебание.
Периодом T называется время, в течение которого материальная точка совершит одно
полное колебание.
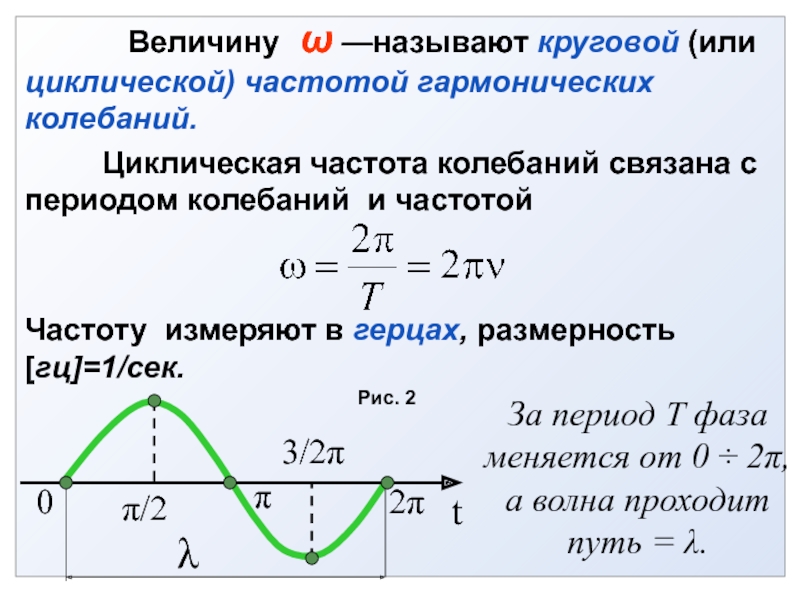
Частотой колебаний называется число пол-
ных колебаний, совершенных в единицу време-
ни, поэтому период и частота колебаний связа-
ны следующим соотношением:
Слайд 16 Пусть тело одновременно участвует в двух
гармонических колебаниях с одинаковыми частотами, но разными амплитудами и начальными
фазами, направленных вдоль одной прямой:( 1 )
Результирующее колебание может быть изображено вектором амплитуды
А = А1 + А2
и вращающимся вокруг т. О с той же угловой ω
(2)
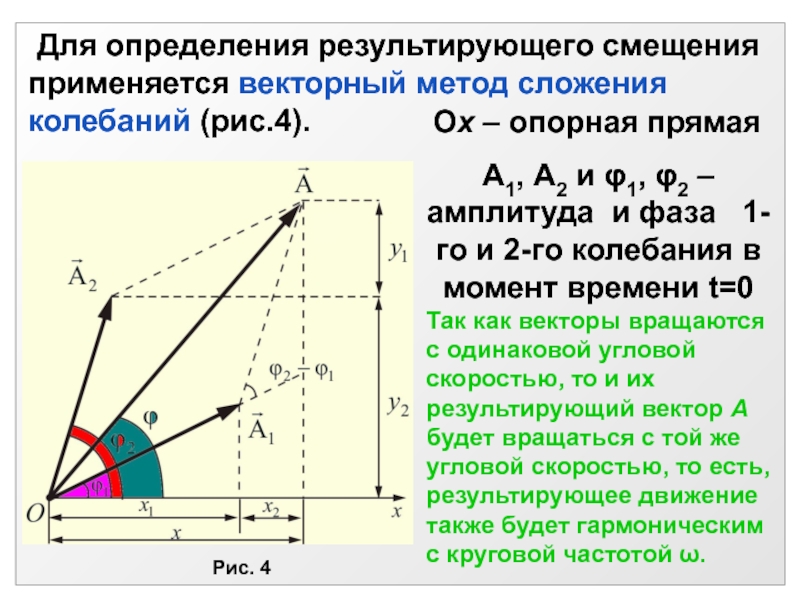
Слайд 17Ox – опорная прямая
A1, А2 и φ1, φ2 – амплитуда
и фаза 1-го и 2-го колебания в момент времени
t=0Так как векторы вращаются с одинаковой угловой скоростью, то и их результирующий вектор А будет вращаться с той же угловой скоростью, то есть, результирующее движение также будет гармоническим с круговой частотой .
Рис. 4
Слайд 18Результирующее колебание определяется уравнением вида
(3 )
Из рис. 4 и
теоремы косинусов видно, что
(4 )
Начальная фаза определяется из соотношения
(5)
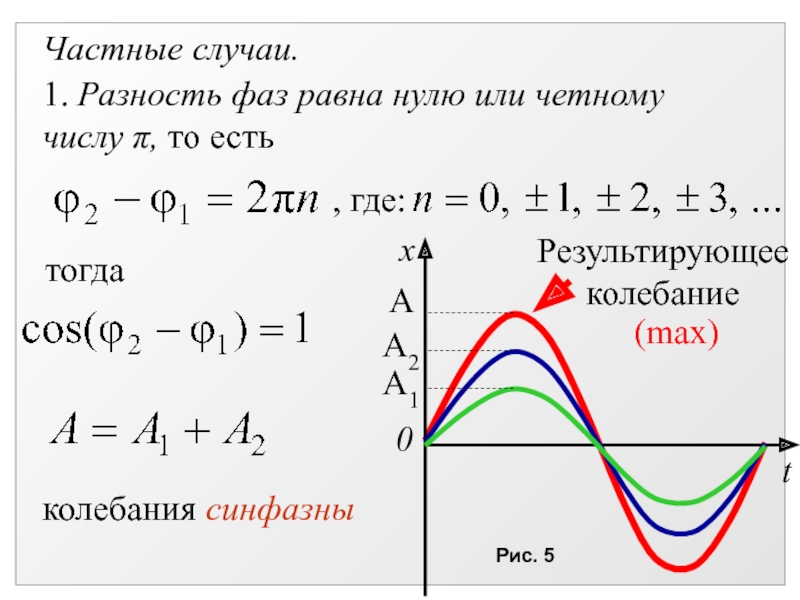
Слайд 191. Разность фаз равна нулю или четному числу π, то
есть
Частные случаи.
, где:
тогда
колебания синфазны
А1
А2
А
х
t
0
Результирующее колебание
(max)
Рис. 5
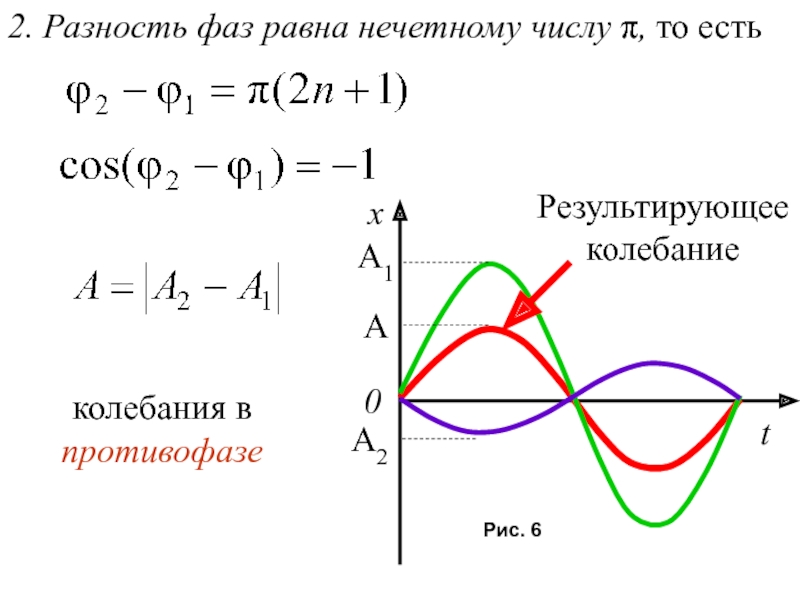
Слайд 20Результирующее колебание
2. Разность фаз равна нечетному числу π, то есть
колебания в противофазе
А1
А2
А
х
0
t
Рис. 6
Слайд 21
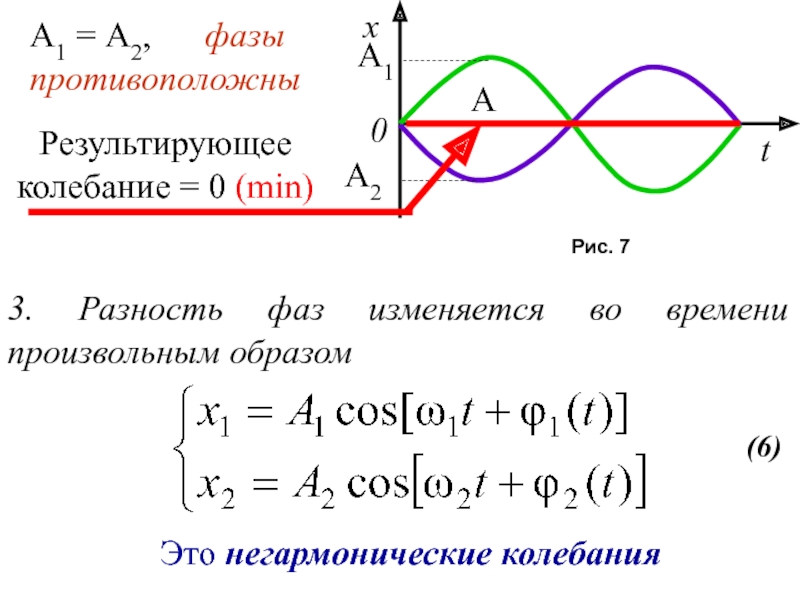
3. Разность фаз изменяется во времени произвольным образом
Это
негармонические колебания
(6)
Результирующее колебание = 0 (min)
А1
А2
А
х
0
t
А1 = А2,
фазы противоположныРис. 7
Слайд 24(10)
Метод биений используется для настройки му-
зыкальных инструментов, анализа слуха и
т.д.
Рис. 9
Слайд 25
2.3.6. Затухающие колебания
В реальных
условиях на тело со стороны
окружающей среды действуют силы трения,
препятствующие движению.
На преодоление сил трения расходуется
энергия. Вследствие этого, энергия колеблюще-
гося тела уменьшается и, следовательно,
уменьшается амплитуда колебаний, т.е.
колебания становятся затухающими.
Запишем второй закон Ньютона для реаль-
ных условий:
(1)
Слайд 302.3.7. Вынужденные колебания
Вынужденными называются колебания,
которые
возникают в системе под действием
внешней силы, изменяющейся по периодичес-
кому
закону, например,F0 - амплитуда вынуждающей силы, - ее круго-
вая частота.
Тогда второй закон Ньютона запишется:
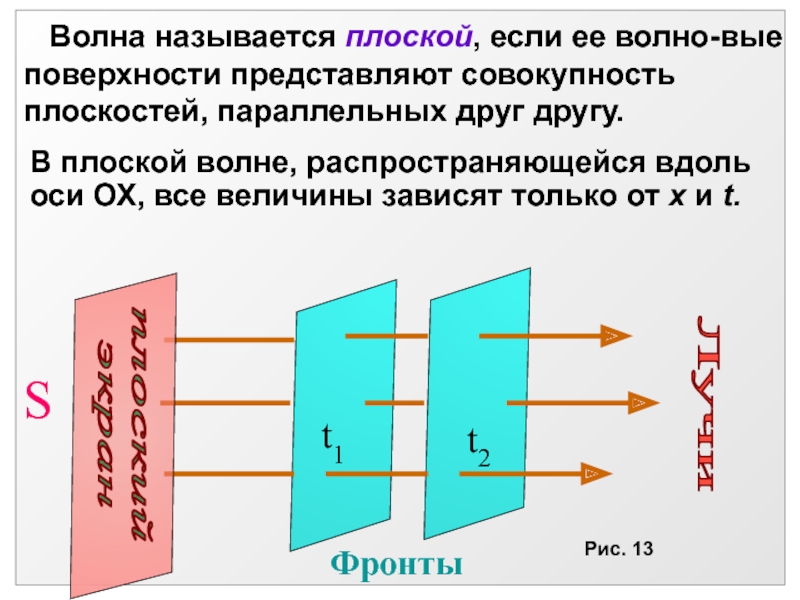
Слайд 36 Волна называется плоской, если ее волно-вые поверхности представляют
совокупность плоскостей, параллельных друг другу.
Лучи
Фронты
В плоской волне, распространяющейся вдоль
оси ОХ, все величины зависят только от х и t.S
плоский
экран
t1
t2
Рис. 13
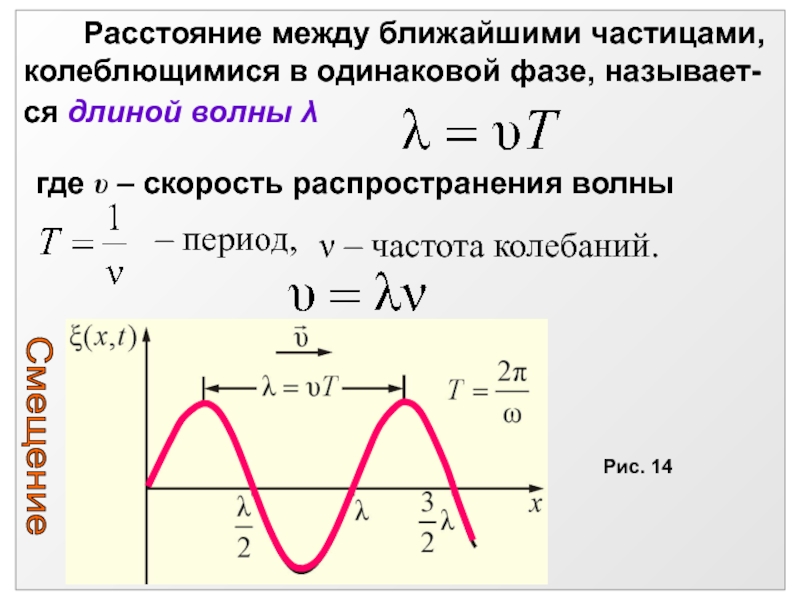
Слайд 37 Расстояние между ближайшими частицами,
колеблющимися в одинаковой
фазе, называет-
ся длиной волны
где υ – скорость распространения
волны – период,
– частота колебаний.
Смещение
Рис. 14
Слайд 382.3.9. Звук
Понятие звука обычно ассоциируется у нас со
слухом и, следовательно, с физиологическими
процессами в ушах, а также
с процессами в на-шем мозгу (там происходит переработка ощуще-
ний, поступающих в органы слуха).
Кроме того, под звуком мы понимаем физичес-
кое явление, вызывающее действие на наши
уши, а именно продольные волны.
При рассмотрении звука можно выделить три
основных аспекта.
Во-первых, должен существовать источник звука;
Во-вторых, энергия переносится от источника
звука в виде продольных звуковых волн.
И, в-третьих, звук регистрируется нашим ухом
или прибором.
Слайд 39 Скорость звука в различных веществах имеет
разные значения.
В воздухе при температуре 0°С и давлении 1 атм звук
распространяется со скоростью 331,3 м/с. Скорость звука зависит от модуля упругости и плотности вещества.
В жидкостях и твердых телах, которые
значительно менее сжимаемы, скорость рас-
пространения звука больше, чем в газах.
Частоты колебаний звуковых волн лежат в
пределах от 16 Гц до 20000 Гц.
Если частоты колебаний ниже 16 Гц, то такие
волны называют инфразвуком, выше 20000 Гц
– ультразвуковые волны.
Слайд 40 Опыт показывает, что инфразвуковые волны
затухают слабо. Поэтому
ослабление инфразву-
ковой волны вызвано только перераспределе-
нием энергии по возрастающему фронту
волны, если волна близка к сферической.
Если же источником является ветровое волнение моря,
где длина фронта волны составляет сотни метров, то
здесь интенсивность инфразвуковой волны мало меня-
ется с расстоянием.
По-видимому, у рыб и морских животных имеется
чувствительность к инфразвукам, благодаря чему они
чувствуют приближение, шторма.
Мощные инфразвуковые волны, возникающие при
шторме, практически без затухания распространяются
в море на расстояния в сотни и тысячи километров и
сигнализируют о его приближении.
Слайд 41Ультразвуковые волны отличаются от слышимого звука
большой частотой колебаний, поэтому
длина волны
ультразвука значительно меньше длины волны звука.
Интенсивность ультразвуковой
волны пропорциональна квадрату амплитуды волны и квадрату частоты колеба-
ний, поэтому ультразвуковые волны имеют большую
интенсивность. Высокая частота позволяет получить
волны с интенсивностями до 100 Вт/см2=10 кВт/м2.
При таких больших интенсивностях ультразвуковая
волна влияет на свойства вещества и ход технологичес-
ких процессов.
Также в медицине при помощи ультразвука осуществля-
ют сварку сломанных костей, диагностические исследо-
вания и т.д. Биологическое действие ультразвука (при-
водящее к гибели микробов) позволяет использовать
его для стерилизации лекарственных веществ, а также
медицинских инструментов.