Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 4 Сила и импульс (Force & Momentum) Лектор: доцент НИЯУ МИФИ,
Содержание
- 1. Лекция 4 Сила и импульс (Force & Momentum) Лектор: доцент НИЯУ МИФИ,
- 2. Дальнодействующие силы. Гравитационные. Притяжение
- 3. Гравитационные силыСила тяжести вблизи поверхности Земли F
- 4. Гравитационные силы на космических расстоянияхF12F21m2m1Гравитационные силы на
- 5. Четвертый закон НьютонаЭкспериментально впервые закон всемирного тяготения
- 6. Четвертый закон НьютонаВАЖНО: инерционная масса и гравитационный
- 7. Закон КулонаОчень похож на закон всемирного тяготения
- 8. Гравитационные силыи ускорение свободного паденияF-FmMR12=R+hF = GMm / (R + h)2если h
- 9. Контактные силы. Вес. Реакция опорыP (вес)N (реакция
- 10. Невесомость. Первая космическая скоростьanVRF = mg =>
- 11. НевесомостьВес - сила, с которой тело действует
- 12. Силы упругости связаны с деформацией контактирующих тел,
- 13. В механике и технике используют специальные устройства,
- 14. Силы упругости. Модуль ЮнгаДля твердых тел (стержней):Здесь
- 15. Силы трения возникают при соприкосновении двух тел
- 16. Трение покоя Трение скольженияСилы трения. Трение покоя и
- 17. Силы трения на наклонной плоскости. Вес.NyxάFтрmgx: ma
- 18. NyxαmaFтрmgx: ma = mg sin(α) - Fтрy:
- 19. Силы трения. Трение каченияVFтрТрение качения - частный
- 20. VСила сопротивления среды - особый вид трения.
- 21. Задача о торможении объекта силой «жидкого» трения
- 22. Импульс.Второй закон Ньютона: mdv/dt = d(mv)/dt =
- 23. Замкнутая система = совокупность попарно взаимодействующих материальных
- 24. Внутренние силы системы не меняют суммарный импульс
- 25. Спасибо за внимание!Продолжение следует!Курс общей физики НИЯУ МИФИ
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Дальнодействующие силы.
Гравитационные.
Притяжение малых тел большими у
их поверхности (сила тяжести)
Гравитационные силы на космических расстояниях
Электромагнитное дальнодействие
Электростатические силы
Магнитные силы
Контактные.
(все имеют электромагнитную природу)
Вес, реакция опоры
Сила упругости
Сила трения и сопротивление среды
Виды сил в механике
Слайд 3Гравитационные силы
Сила тяжести вблизи поверхности Земли
F = mg
Сила
тяжести почти не зависит от расстояния до поверхности (до тех
пор, пока оно невелико) и направлена всегда в одну сторону (вниз, к центру притяжения)g =~ 9,81 м/с2 - ускорение свободного падения.
Ускорение свободного падения несильно зависит от географической широты (от 9,78 на экваторе до 9,82 на полюсах) из-за вращения Земли и ее не совсем сферической формы
Слайд 4Гравитационные силы на космических расстояниях
F12
F21
m2
m1
Гравитационные силы на космических расстояниях зависят
от расстояния между центрами взаимодействующих тел (центральные силы) и равны
(четвертый Закон Ньютона):R12
R12 - радиус-вектор, от центра первого тела к центру второго.
R = | R12 |
F12 = - F21 = - G m1 m2 R12 / R3
По абсолютной величине
F12 = F21 = Gm1m2 /R2
G = 6.67•10-11 н•м2/ кг2 - гравитационная постоянная.
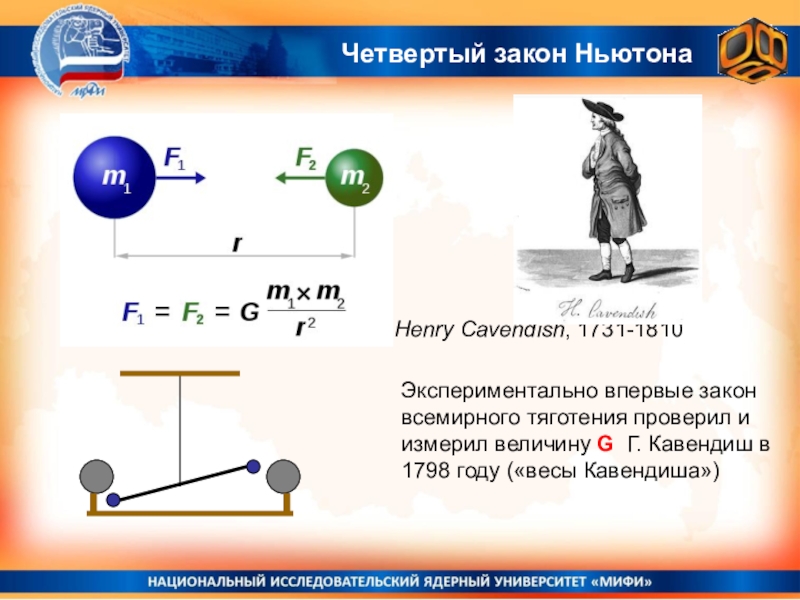
Слайд 5Четвертый закон Ньютона
Экспериментально впервые закон всемирного тяготения проверил и измерил
величину G Г. Кавендиш в 1798 году («весы Кавендиша»)
Henry Cavendish,
1731-1810Слайд 6Четвертый закон Ньютона
ВАЖНО: инерционная масса и гравитационный заряд – разные
физические величины! Гравитационный заряд, например, можно определить как q =
m√G и измерять в м√Н - и в законе всемирной гравитации константа G будет равна 1.F = q1q2/r2.
Удивительно, но масса инерционная (из второго закона Ньютона) и масса гравитационная (гравитационный заряд из четвертого) строго пропорциональны друг другу, а в системе СИ - тождественно равны.
Слайд 7Закон Кулона
Очень похож на закон всемирного тяготения и закон взаимодействия
электрических зарядов, экспериментально установленный Ш. Кулоном тоже с помощью крутильных
весов в 1780-ые годыCharles Augustine de Coulomb, 1736-1806
F = kq1q2/r2.
Постоянная закона Кулона k в системе СИ всемирной гравитации константа G будет равна 9*109 Н*м2/Кул2, а в Гауссовой (физической) системе единиц k = 1
Слайд 8Гравитационные силы
и ускорение свободного падения
F
-F
m
M
R12=R+h
F = GMm / (R +
h)2
если h
= mgгде g = GM / R2 = ~ 9,81 м/с2 – «стандартное» ускорение свободного падения
M = ~ 6,0x1024 кг - масса Земли
R = ~ 6,4x106 м - радиус Земли
G = ~ 6,67х10-11 нм2/ кг2 - гравитационная постоянная
R
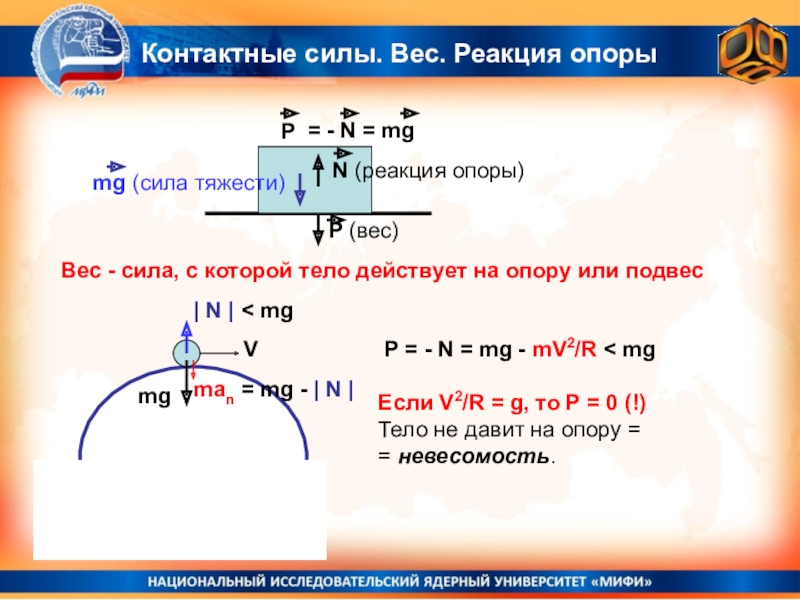
Слайд 9Контактные силы. Вес. Реакция опоры
P (вес)
N (реакция опоры)
P
= -
N = mg
Вес - сила, с которой тело действует на
опору или подвес | N | < mg
man = mg - | N |
mg
V
P = - N = mg - mV2/R < mg
Если V2/R = g, то Р = 0 (!)
Тело не давит на опору =
= невесомость.
mg (сила тяжести)
Слайд 10Невесомость. Первая космическая скорость
an
V
R
F = mg => man = mV2/R
=> N = P = 0
V1 = (g R)1/2 =
~7,9 км/с - первая космическая скорость (скорость свободного полета спутника на низкой круговой околоземной орбите) Сам спутник и все, что внутри него пребывает в состоянии невесомости.
Для высоких орбит ( H ~R или H > R):
F = GMm / (R + Н)2 < GMm /R2 = mg
v = ((R+H)F/m)1/2 = (GM / (R + Н))1/2 < 7,9 км/с
Геостационарные орбиты: T = 24часа; H ~ 40 т.км
V
R+Н
Слайд 11Невесомость
Вес - сила, с которой тело действует на опору или
подвес
F = mg = ma
=> N = P = 0
Cвободный
полет = движение по баллистической траектории -> ускорение = g, вес тела = 0Слайд 12Силы упругости связаны с деформацией контактирующих тел, приводящей к изменению
расстояний между молекулами и атомами, их составляющими.
Деформация – любое изменение
объема или формы тела. вес, реакция опоры, натяжение нити при подвесе являются частными случаями сил упругости. В этих случаях достаточно малой деформации, чтобы вызвать большие силы. Величиной деформации в таких задачах пренебрегают.
Силы упругости
Слайд 13В механике и технике используют специальные устройства, упругие свойства которых
проявляются при заметных деформациях: пружины, эластичные шнуры, изгибающиеся пластины и
т.п.Fупр = - F
F
ΔX - изменение длины
X
Fупр = - kΔX
k - коэффициент упругости
Силы упругости. Закон Гука.
Закон Гука (Robert Hooke, 1635-1703):
при упругой деформации сила упругости прямо пропорциональна абсолютному значению изменения длины тела и направлена против деформации
Важно:закон Гука справедлив, если деформация не очень велика
Слайд 14Силы упругости. Модуль Юнга
Для твердых тел (стержней):
Здесь коэффициент Е [н/м2]
называется модулем Юнга и характеризует
прочность твердых тел. Для металлов он
составляет 109 - 1011 н/м2Fупр = - kΔX
Слайд 15Силы трения возникают при соприкосновении двух тел и действуют вдоль
поверхности их соприкосновения.
Силы трения связаны со взаимодействием электронных оболочек
атомов соприкасающихся тел = тангенциальная реакция опоры В механике различают:
трение покоя
трение скольжения
трение качения
...
Отдельный случай - силы сопротивления движению твердых тел в газах и жидкостях (см. далее).
Трение существует везде и всюду. Оно может быть полезным (помогает нам ходить, заставляя двигаться автомобили и т.п.) или вредным (мешает скольжению в подшипниках, и др.)
Силы трения
Слайд 16Трение покоя Трение скольжения
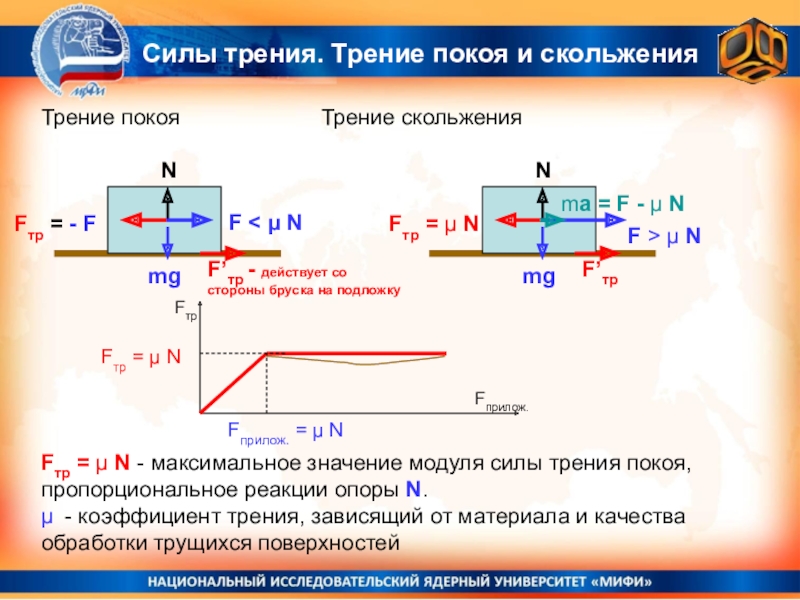
Силы трения. Трение покоя и скольжения
mg
N
F < μ
N
Fтр = - F
F’тр - действует со стороны бруска на
подложкуmg
N
F > μ N
Fтр = μ N
F’тр
ma = F - μ N
Fтр = μ N
Fтр
Fприлож.
Fприлож. = μ N
Fтр = μ N - максимальное значение модуля силы трения покоя, пропорциональное реакции опоры N.
μ - коэффициент трения, зависящий от материала и качества обработки трущихся поверхностей
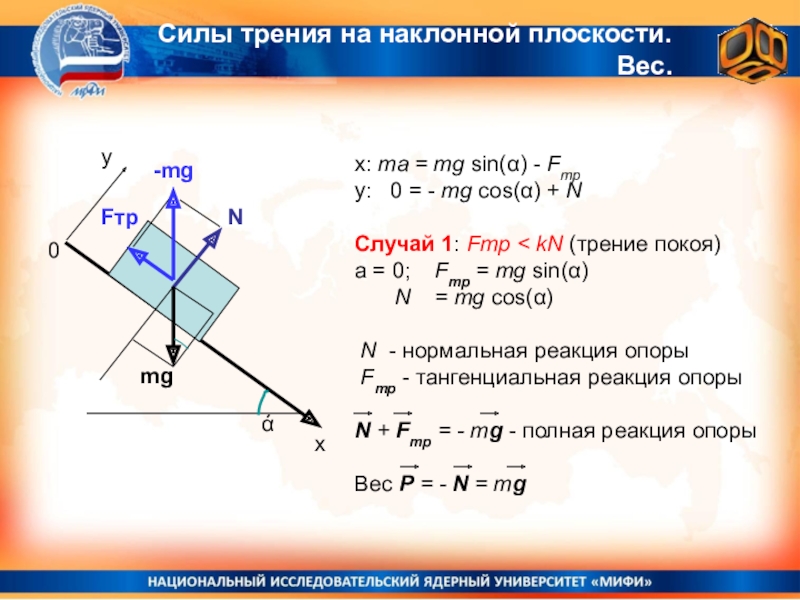
Слайд 17Силы трения на наклонной плоскости.
Вес.
N
y
x
ά
Fтр
mg
x: ma = mg sin(α)
- Fтр
y: 0 = - mg cos(α) + N
Случай
1: Fтр < kN (трение покоя)а = 0; Fтр = mg sin(α)
N = mg cos(α)
N - нормальная реакция опоры
Fтр - тангенциальная реакция опоры
N + Fтр = - mg - полная реакция опоры
Вес Р = - N = mg
0
-mg
Слайд 18N
y
x
α
ma
Fтр
mg
x: ma = mg sin(α) - Fтр
y: 0 =
- mg cos(α) + N
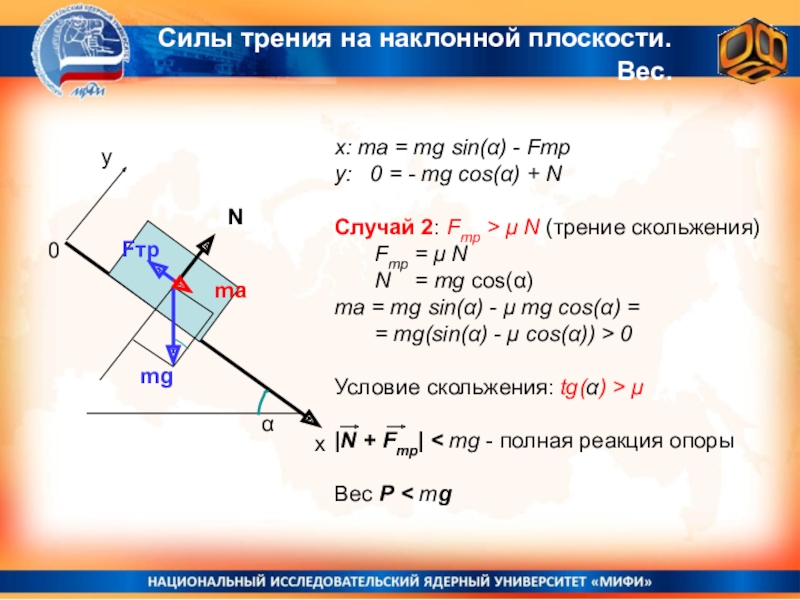
Случай 2: Fтр > μ N
(трение скольжения)Fтр = μ N
N = mg cos(α)
ma = mg sin(α) - μ mg cos(α) =
= mg(sin(α) - μ cos(α)) > 0
Условие скольжения: tg(α) > μ
|N + Fтр| < mg - полная реакция опоры
Вес Р < mg
0
Силы трения на наклонной плоскости.
Вес.
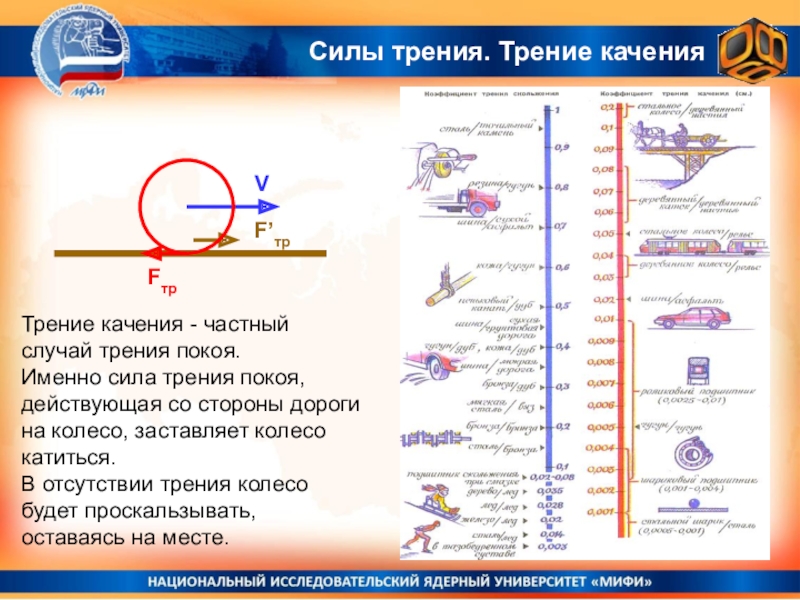
Слайд 19Силы трения. Трение качения
V
Fтр
Трение качения - частный случай трения покоя.
Именно
сила трения покоя, действующая со стороны дороги на колесо, заставляет
колесо катиться.В отсутствии трения колесо будет проскальзывать, оставаясь на месте.
F’тр
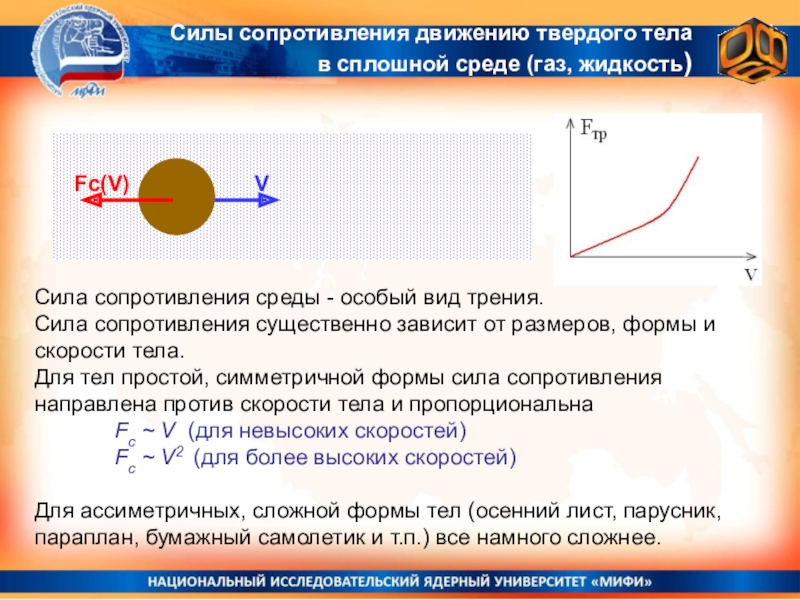
Слайд 20V
Сила сопротивления среды - особый вид трения.
Сила сопротивления существенно
зависит от размеров, формы и скорости тела.
Для тел простой,
симметричной формы сила сопротивления направлена против скорости тела и пропорциональнаFc ~ V (для невысоких скоростей)
Fc ~ V2 (для более высоких скоростей)
Для ассиметричных, сложной формы тел (осенний лист, парусник, параплан, бумажный самолетик и т.п.) все намного сложнее.
Fc(V)
Силы сопротивления движению твердого тела
в сплошной среде (газ, жидкость)
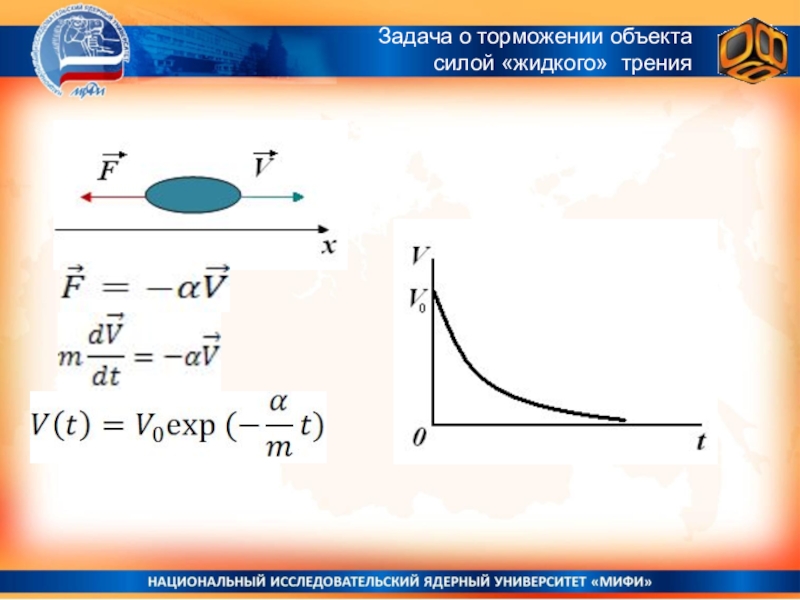
Слайд 22Импульс.
Второй закон Ньютона:
mdv/dt = d(mv)/dt = dp/dt = F
p=
mv) – импульс тела (momentum)
dp = Fdt приращение импульса (импульс
силы)Для пары взаимодействующих тел:
F12
F21
m2
m1
Δ P1 = F21 х Δt
Δ P2 = F12 х Δt = - F12 х Δt = - Δ P1
Суммарный импульс пары взаимодействующих тел остается постоянным:
P1 + dP1 + P2 + dP2 = P1 + F21dt + P2 + F12dt = P1 + P2
Слайд 23Замкнутая система = совокупность попарно взаимодействующих материальных точек. Суммарное изменение
импульса а каждой паре равно нулю => суммарный импульс всей
системы сохраняется:Внутренние силы системы не меняют суммарный импульс системы. Он может измениться только под действием внешних сил.
Закон сохранения импульса: если сумма внешних сил равна нулю (система замкнута) - суммарный импульс системы остается постоянным
Pсист = P1 + P2 + P3 + … = Σ Pi = Const
Закон сохранения импульса
для замкнутой системы частиц
ПРИМЕР: Неупругое столкновение двух тел
m1v1 + m2v2 = (m1 + m2)v
Слайд 24Внутренние силы системы не меняют суммарный импульс системы Рсист. Он
может измениться только под действием внешних сил.
F2
F1
m2
m1
m3
m4
m5
Pсист = m1v1
+ m2v2 + m3v3 + … = MvcM = Σ mi ; vс = (Σ mivi)/M – скорость центра масс системы
vс = (Σ midri /dt)/M = d(Σ miri /M)/dt) = drC /dt
rс = Σ miri //M – радиус-вектор центра масс системы
dPсист = dP1 + dP2 + dP3 + … = dtΣ Fi = dt Fвнеш =>
dPсист / dt = Σ Fi = Fвнеш = Mdvc /dt = Md2rc /dt2
Движение системы частиц
под действием внешних сил
Уравнение движения для системы многих частиц точно такое-же как для одной материальной точки с массой M (масса системы), помещающейся в центре масс системы rс . Это позволяет изучать движение составного объекта как целого, не обращая внимания на его внутреннюю структуру и взаимодействие его частей











![Лекция 4
Сила и импульс
(Force & Momentum)
Лектор:
доцент НИЯУ МИФИ, Силы упругости. Модуль ЮнгаДля твердых тел (стержней):Здесь коэффициент Е [н/м2] называется Силы упругости. Модуль ЮнгаДля твердых тел (стержней):Здесь коэффициент Е [н/м2] называется модулем Юнга и характеризуетпрочность твердых тел.](/img/tmb/6/578679/bbb5bf9ac9387f8b1fde11ac28d8103c-800x.jpg)