Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 5
Содержание
- 1. Лекция 5
- 2. Общие положенияВ данной группе методов исходный базис
- 3. Общие положенияНезависимо от метода преобразования,
- 4. Общие положенияТиповые задачи:Главный элемент – прямаяПрямую общего
- 5. Общие положенияГлавный элемент – плоскость3) Плоскость общего
- 6. Вращение вокруг проецирующих осейСущность метода вращения вокруг
- 7. Преобразование отрезка прямой общего положения в прямую
- 8. Решение: Отрезок проецируется на плоскость проекций в
- 9. На плоскости П2 проекция точки В перемещается
- 10. Преобразование отрезка прямой общего положения в проецирующий
- 11. Преобразование плоскости общего положения в проецирующую (3
- 12. Преобразование плоскости общего положения в проецирующую и
- 13. Преобразование плоскости общего положения в плоскость уровня
- 14. Преобразование плоскости общего положения в плоскость уровня
- 15. Решение: Гл.элемент преобразования – плоскость.1) Преобразуем плоскость
- 16. Все точки фигуры движутся одновременно и останавливаются,
- 17. Соединяем проекции точек 11‘ и С1' ,
- 18. Все точки фигуры, вращаясь вокруг оси
- 19. 2)Преобразуем проецирующую плоскость в плоскость уровняЗададим вторую
- 20. Т.к. на П2 проекции точек А2'‘ и
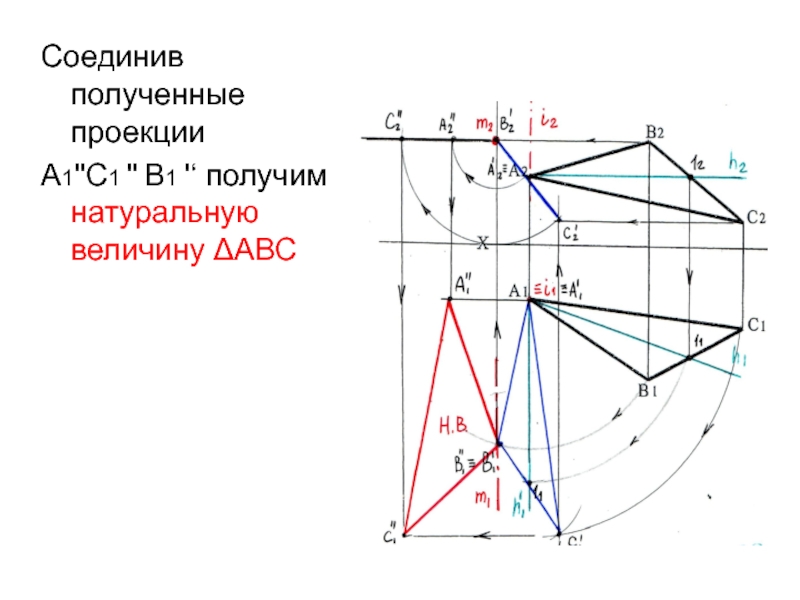
- 21. Соединив полученные проекции А1''С1 '' В1 '‘ получим натуральную величину ΔАВС
- 22. Вращение вокруг линий уровняЭтот способ применяется для
- 23. Рассмотрим примерыЗадача 7.3 стр.35 : Определить натуральную
- 24. Решение:Зададим в плоскости АВС фронталь на любом
- 25. Т.к. фронталь является осью вращения, точки 1
- 26. Так как плоскость АВС должна развернуться параллельно
- 27. Траектория вращения точки В на П2 проецируется
- 28. Точка В развернулась в положение, параллельное П2.Угол
- 29. Задача 7.4 стр.35Определить натуральную величину треугольника АВС вращением вокруг горизонтали
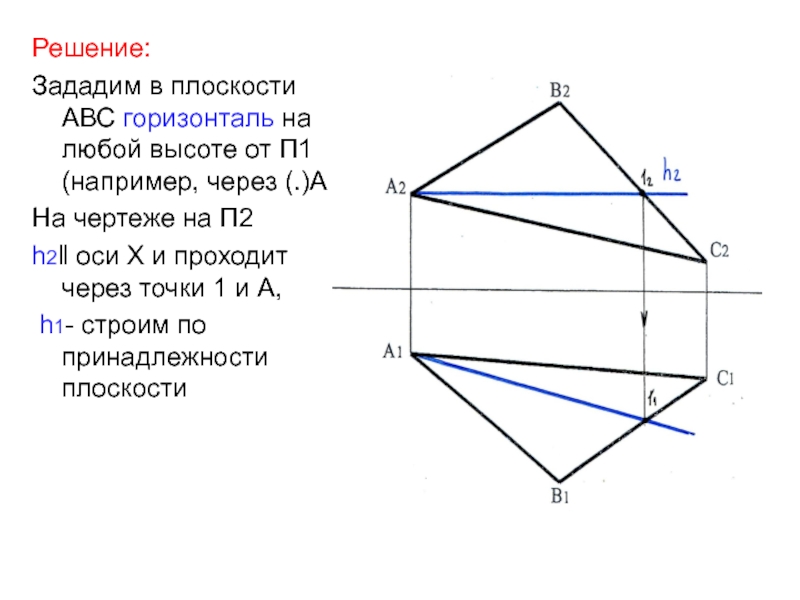
- 30. Решение:Зададим в плоскости АВС горизонталь на любой
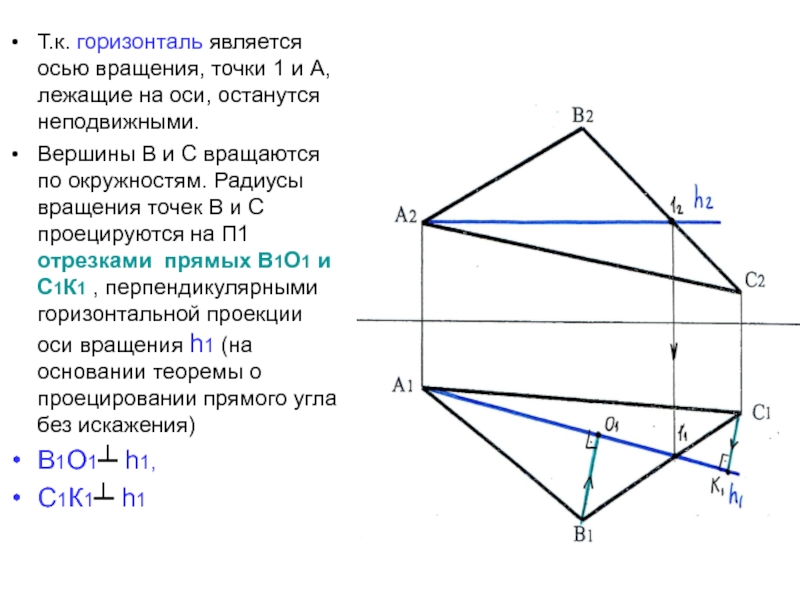
- 31. Т.к. горизонталь является осью вращения, точки 1
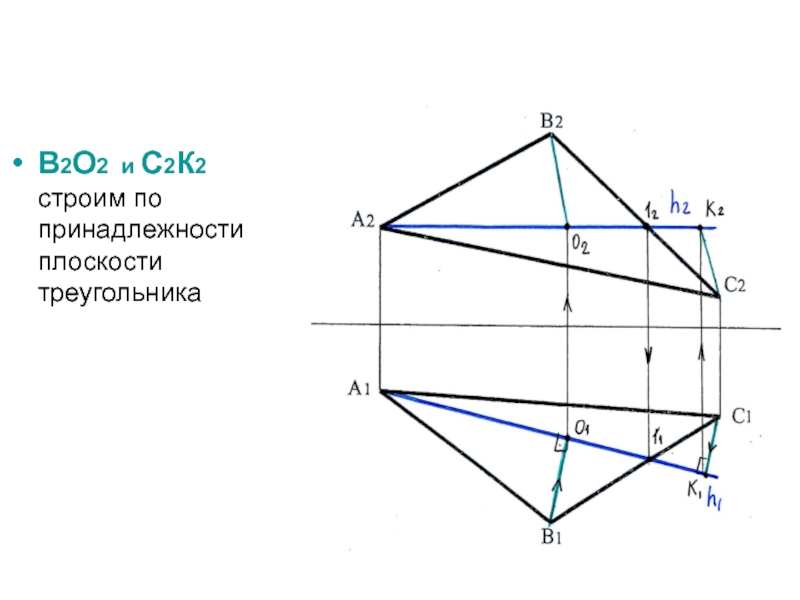
- 32. В2О2 и С2К2 строим по принадлежности плоскости треугольника
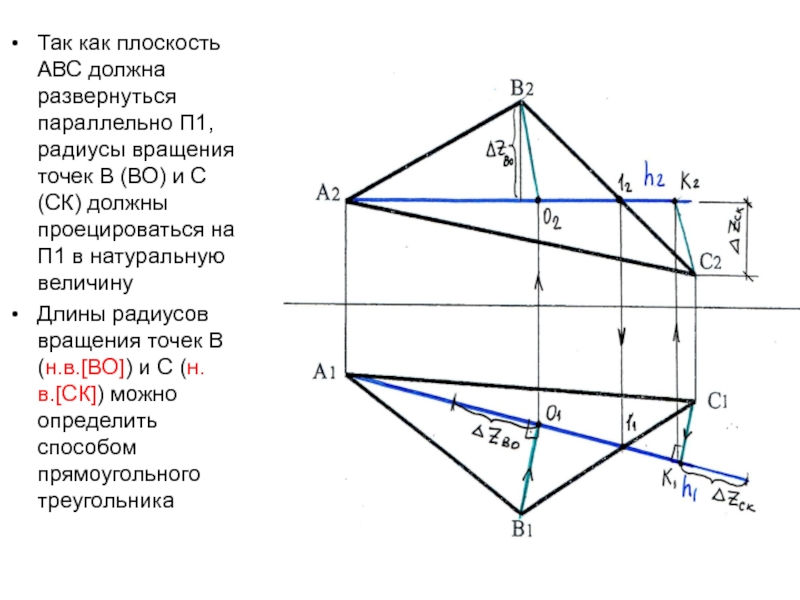
- 33. Так как плоскость АВС должна развернуться параллельно
- 34. Слайд 34
- 35. Траектория вращения точки ВТраектория вращения точки С___________________________Траектории
- 36. Отложим по траектории вращения точки В отрезок
- 37. Метод плоскопараллельного перемещенияСущность метода плоско-параллельного перемещениясостоит в
- 38. Преобразование отрезка прямой общего положения в прямую
- 39. Преобразование отрезка прямой общего положения в проецирующийЗадача
- 40. Задача 7.7 стр.37:Найти расстояние от точки А
- 41. Если прямая ВС преобразуется в проецирующую, то
- 42. Вместе с главным элементом перемещается и (.)А,
- 43. Все точки объекта движутся параллельно П1, поэтому на П2 фронтальные проекции точек смещаются параллельно оси Х
- 44. По линиям связи находим новое положение фронтальных проекций точек В2',С2 ' и А2 '
- 45. Отрезок ВС проецируется в натуральную величину (промежуточный результат)
- 46. Преобразуем главный элемент- отрезок прямой ВС в
- 47. На П1 проекции точек движутся параллельно оси
- 48. Находим недостающую проекцию АО на П2. Т.к.
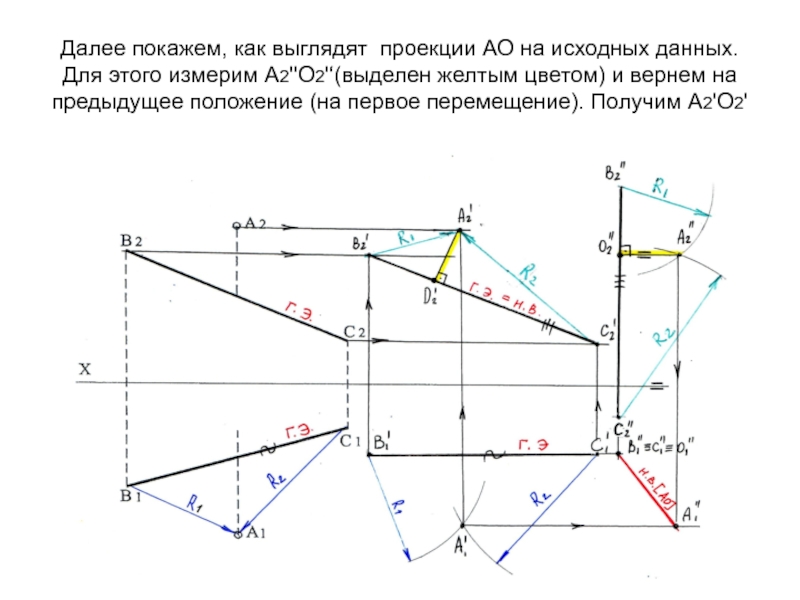
- 49. Далее покажем, как выглядят проекции АО на
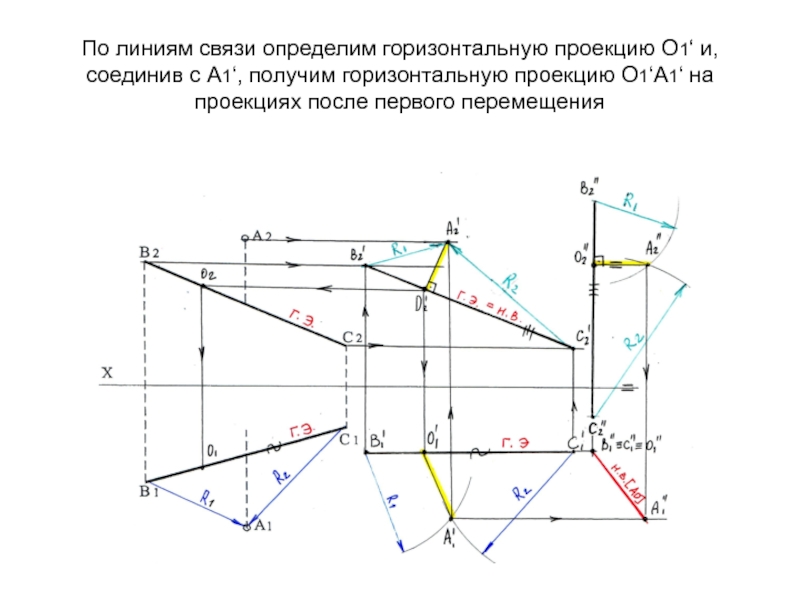
- 50. По линиям связи определим горизонтальную проекцию О1‘
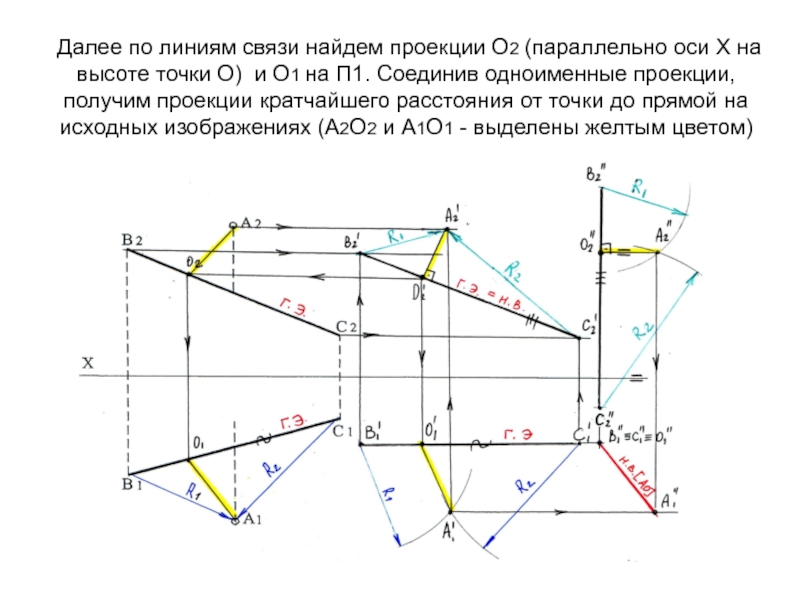
- 51. Далее по линиям связи найдем проекции О2
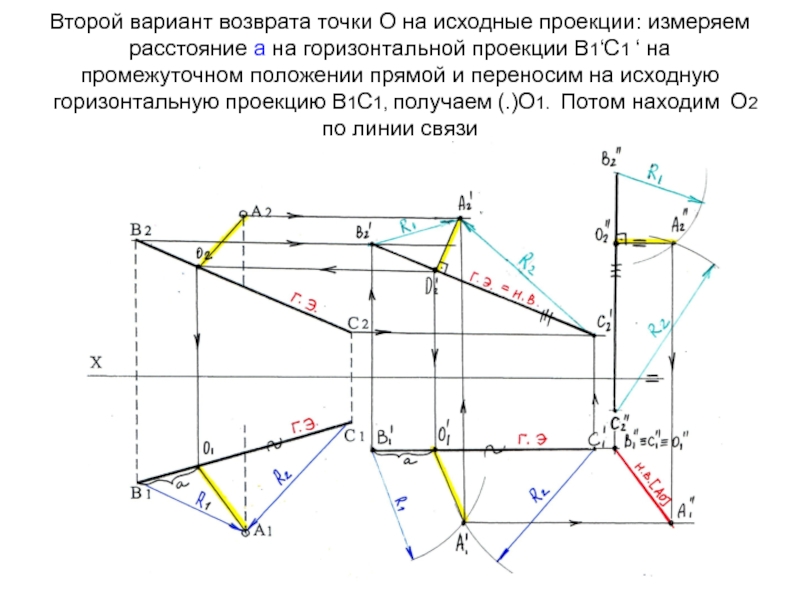
- 52. Второй вариант возврата точки О на исходные
- 53. Определение расстояния между параллельными прямыми способом плоскопараллельного
- 54. Выбираем главный элемент преобразования- например АВ (Г.Э.)
- 55. Т.к. вместе с главным элементом АВ перемещается
- 56. Т.к. прямые параллельны, то и при развороте
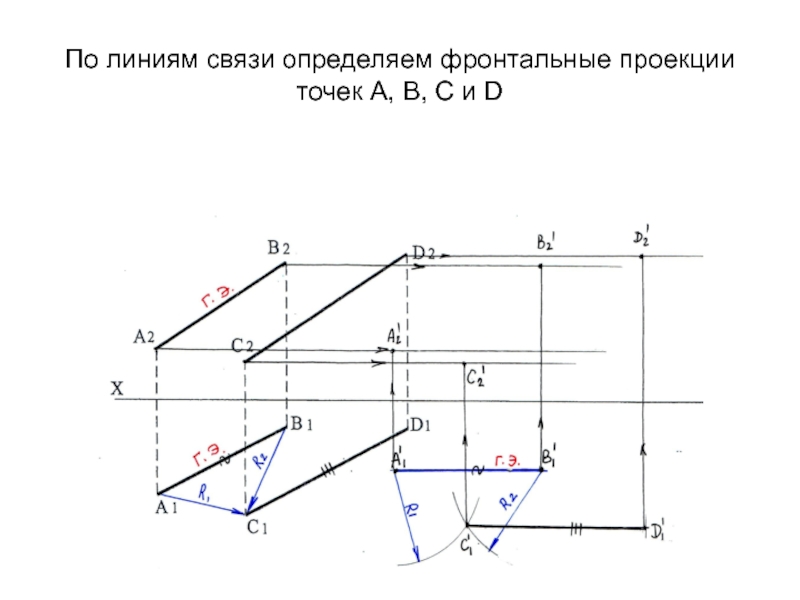
- 57. По линиям связи определяем фронтальные проекции точек А, В, С и D
- 58. На П2 фронтальные проекции прямых в новом
- 59. Выполняем второе перемещение –преобразуем отрезок АВ (Г.Э.)
- 60. Т.к. вместе с АВ параллельно плоскости П2
- 61. Строим фронтальную проекцию С2'‘D2'‘ после второго перемещения
- 62. Натуральная величина расстояния между параллельными прямыми находится
- 63. Возвращаем проекции ВК на исходные позиции.
- 64. Возвращаем проекции ВК на исходные позиции. Можно
- 65. Определение натуральной величины двугранного углаГлавный элементЧтобы
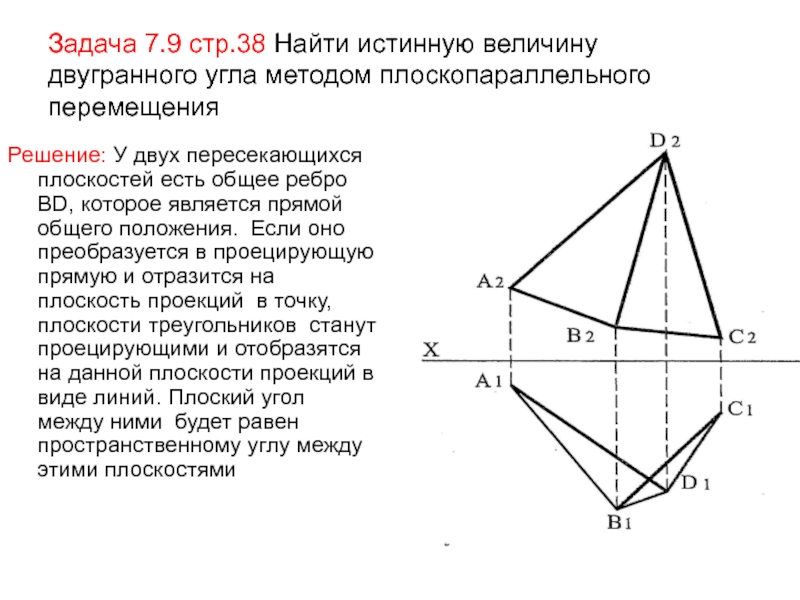
- 66. Задача 7.9 стр.38 Найти истинную величину двугранного
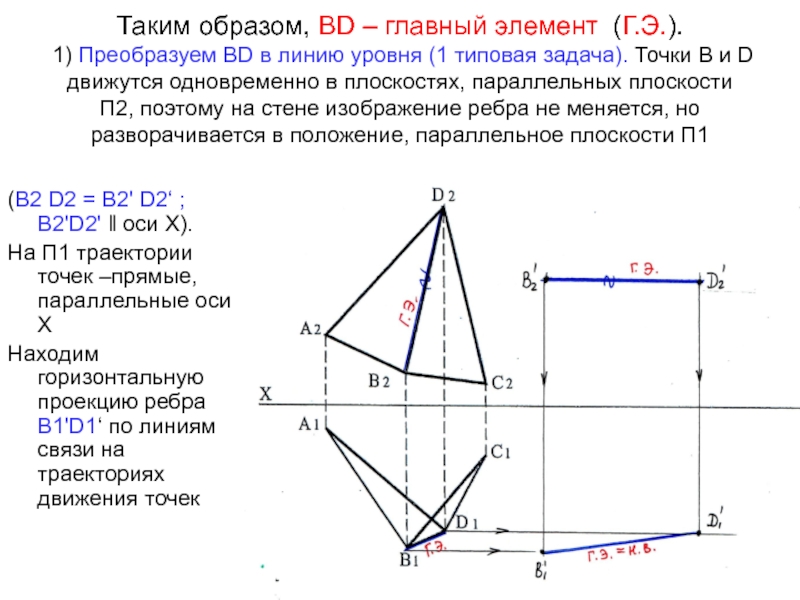
- 67. Таким образом, ВD – главный элемент (Г.Э.).
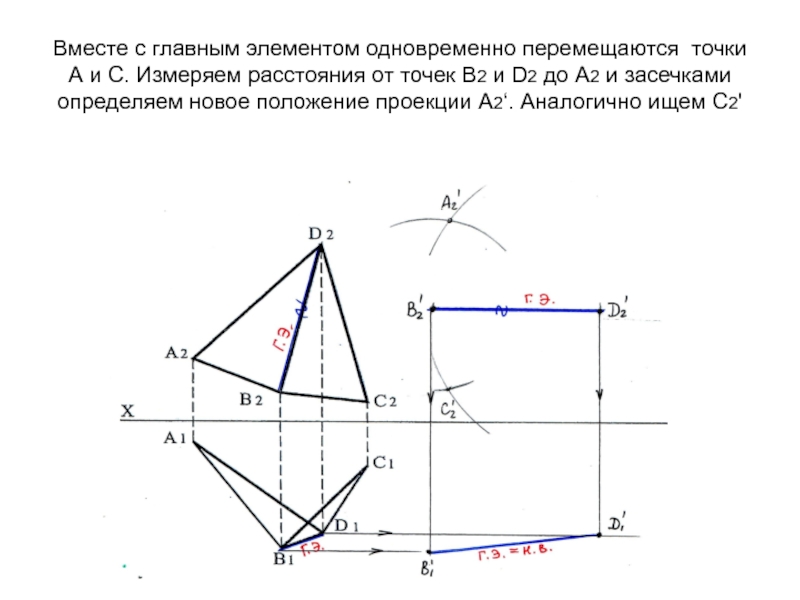
- 68. Вместе с главным элементом одновременно перемещаются точки
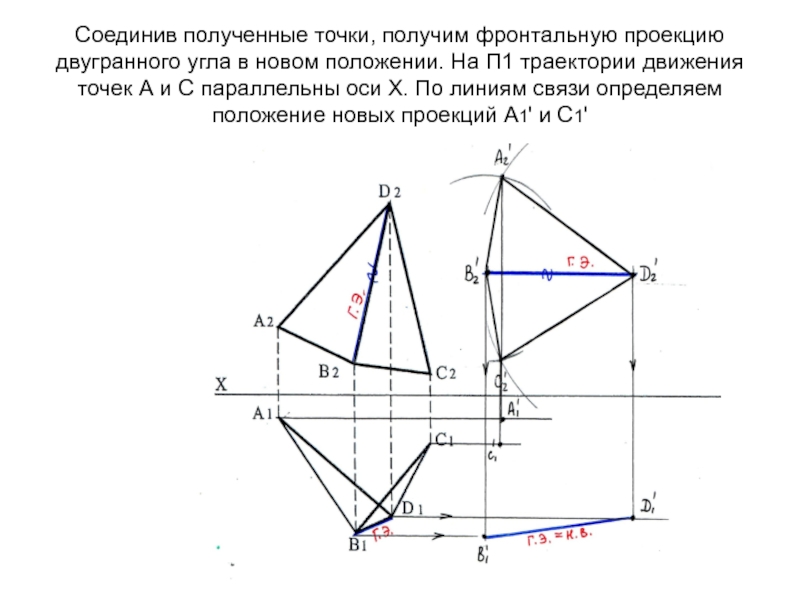
- 69. Соединив полученные точки, получим фронтальную проекцию двугранного
- 70. Соединяем полученные проекции точек на П1- получаем
- 71. 2)Преобразуем ребро ВD в положение проецирующей прямой.
- 72. Т.к. движение переноса осуществляется параллельно П1, проекция
- 73. Определяем новое положение точки А1'‘ засечками, измеряя
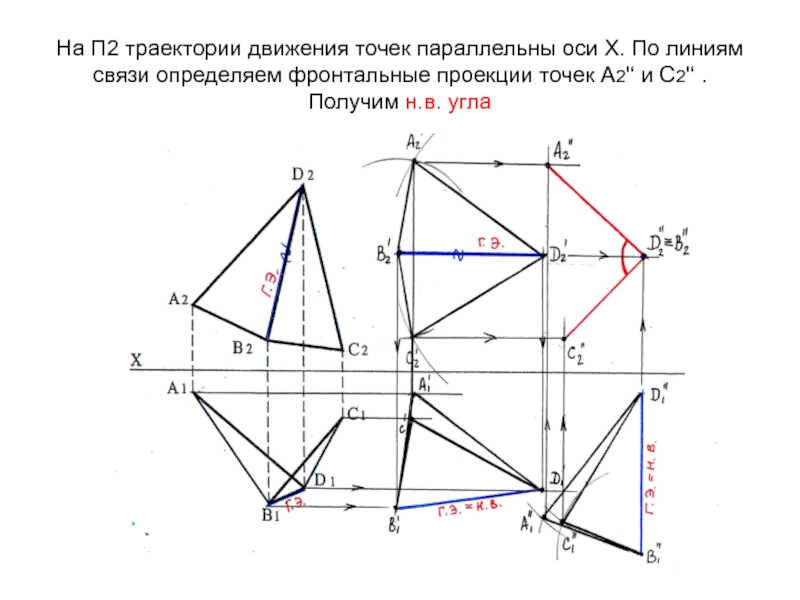
- 74. На П2 траектории движения точек параллельны оси
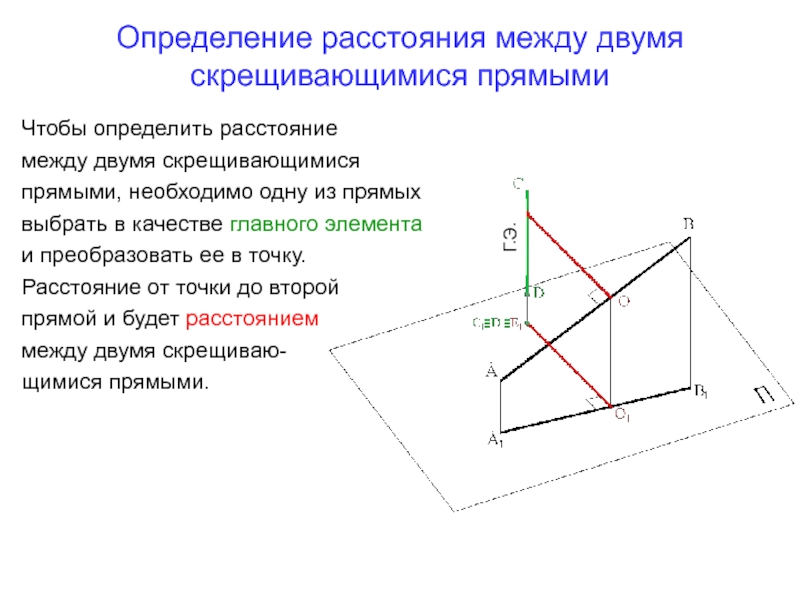
- 75. Определение расстояния между двумя скрещивающимися прямымиГ.Э.Чтобы определить
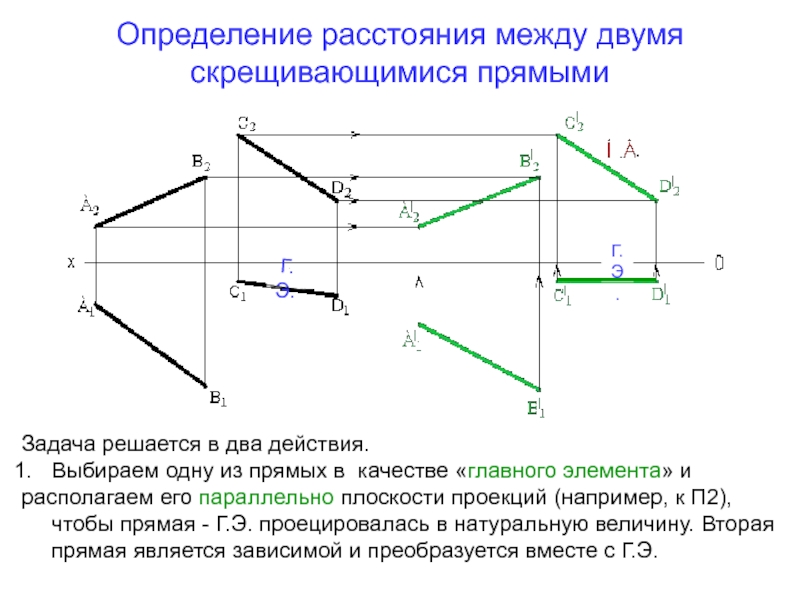
- 76. Определение расстояния между двумя скрещивающимися прямымиГ.Э.Г.Э.Задача решается
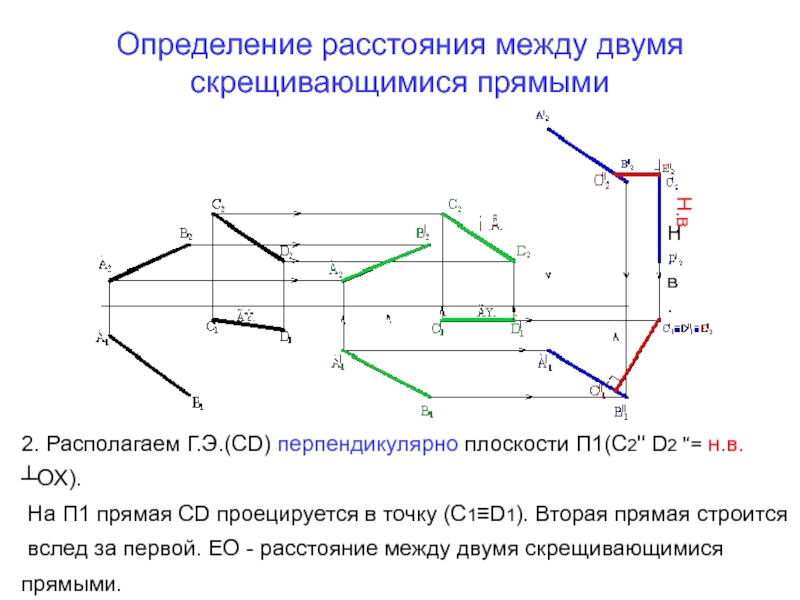
- 77. Определение расстояния между двумя скрещивающимися прямыми Н.в.Н.в.2.
- 78. Преобразование плоскости общего положения в проецирующую и
- 79. Определение натуральной величины плоской фигурыЗадача решается
- 80. Задача 7.5 стр.36 Определить натуральную величину
- 81. 1) Преобразуем плоскость в положение проецирующейДля этого
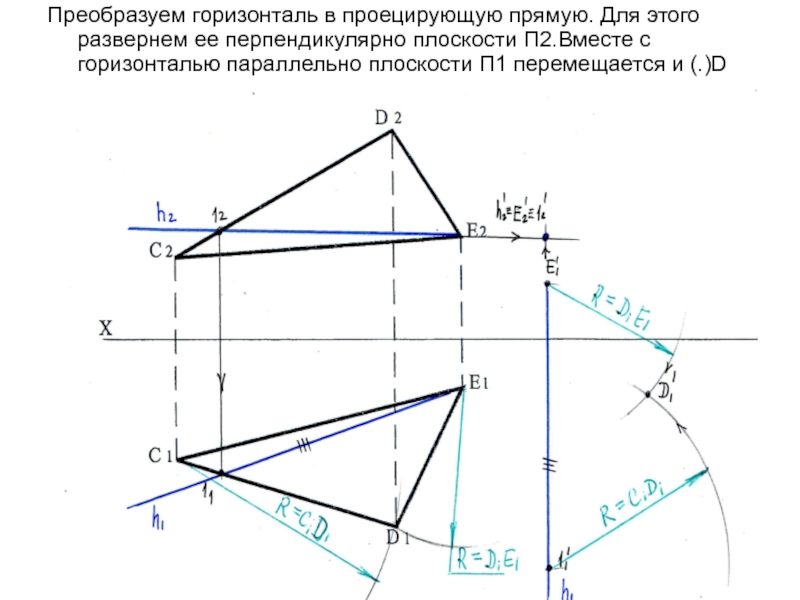
- 82. Преобразуем горизонталь в проецирующую прямую. Для
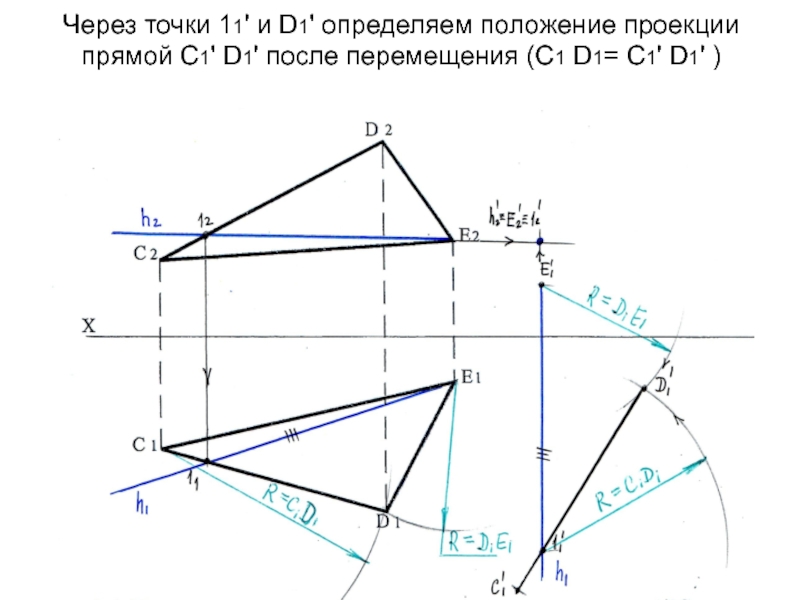
- 83. Через точки 11' и D1' определяем положение
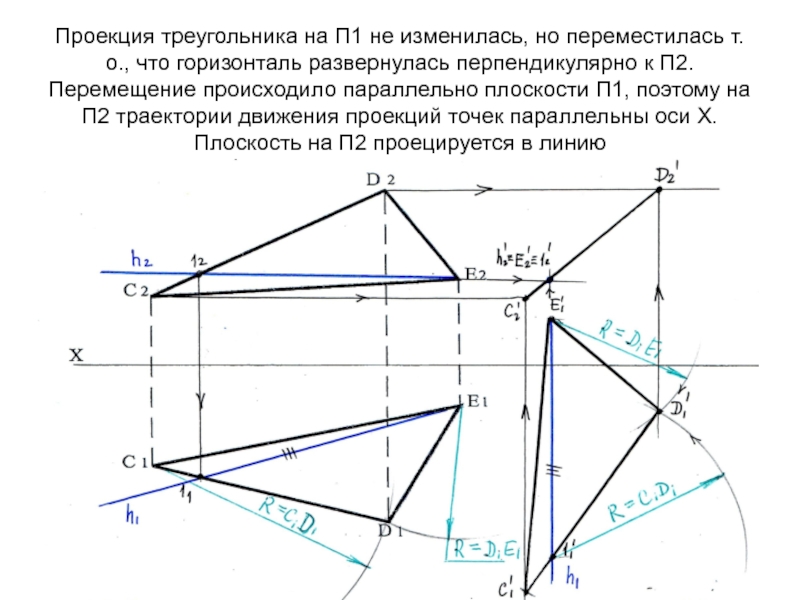
- 84. Проекция треугольника на П1 не изменилась, но
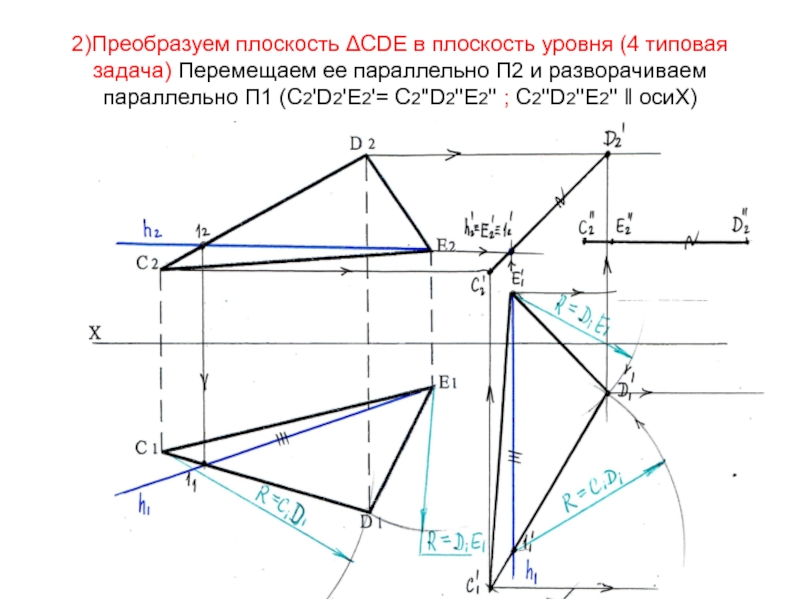
- 85. 2)Преобразуем плоскость ΔСDЕ в плоскость уровня (4
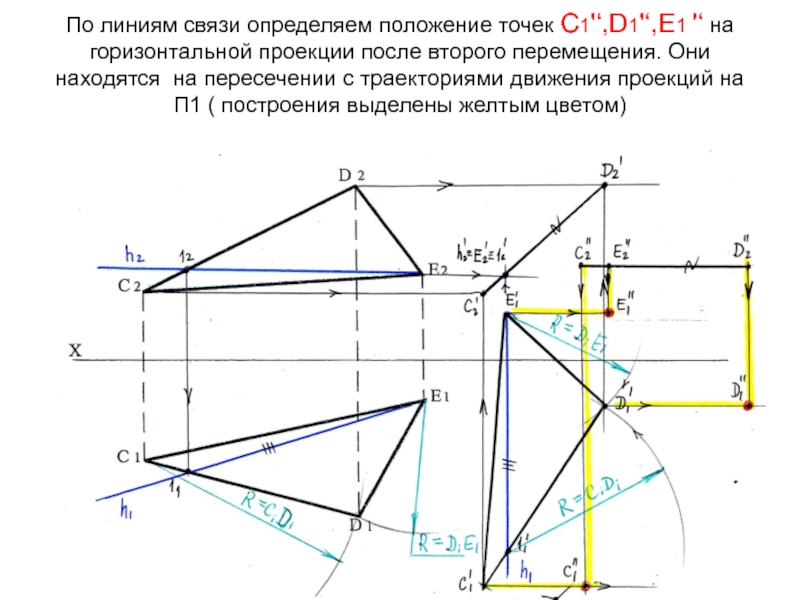
- 86. По линиям связи определяем положение точек С1'‘,D1'‘,Е1
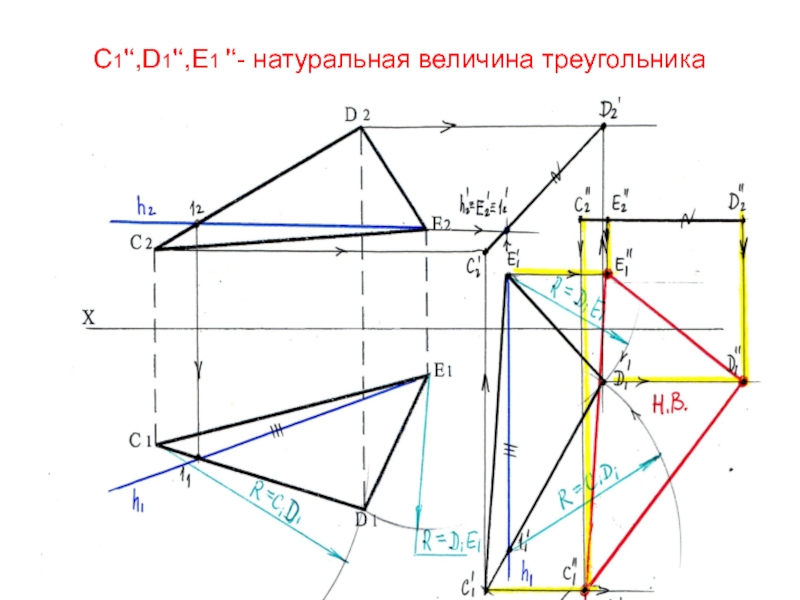
- 87. С1'‘,D1'‘,Е1 '‘- натуральная величина треугольника
- 88. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 5
Методы преобразования плоскостей проекций.
Вращение вокруг проецирующих осей.
Вращение вокруг линии
уровня
Слайд 2Общие положения
В данной группе методов исходный базис (П1 иП2) жестко
зафиксирован в пространстве. Объект перемещается (вращается) так, чтобы он отразился
на исходные плоскости П1 и П2 в удобном для решения задачи положенииСлайд 3Общие положения
Независимо от метода преобразования, в
задаче выделяется главный элемент, с которым и выполняются преобразования. Все
остальные элементы (объекты) задачи являются зависимыми от главного и преобразуются вместе с ним.Главным элементом может быть прямая или плоскость
Слайд 4Общие положения
Типовые задачи:
Главный элемент – прямая
Прямую общего положения преобразовать в
линию уровня
L→ L‘ ‖ П
2) Прямую общего
положения преобразовать в проецирующуюL→ L‘‘┴ П
Слайд 5Общие положения
Главный элемент – плоскость
3) Плоскость общего положения преобразовать в
проецирующую
α→ α‘ ┴ П
4) Плоскость общего положения
преобразовать в плоскость уровняα → α‘‘ ‖ П
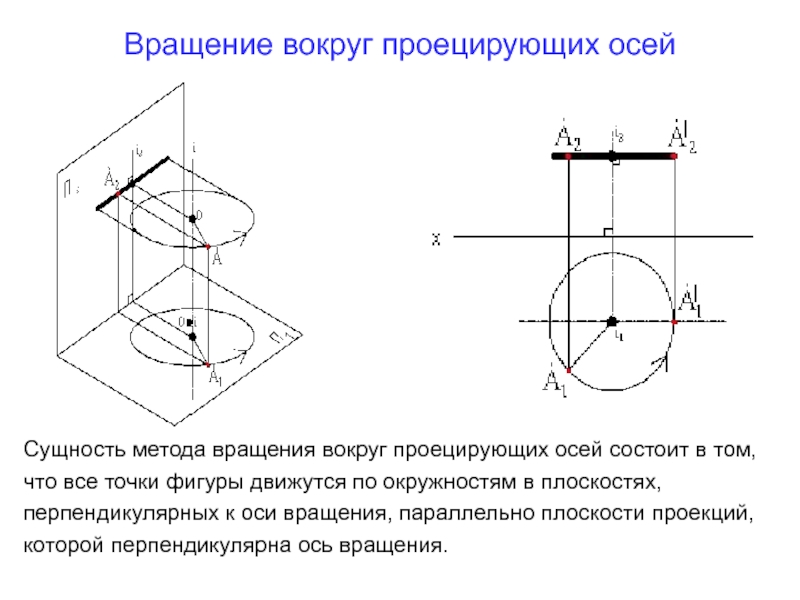
Слайд 6Вращение вокруг проецирующих осей
Сущность метода вращения вокруг проецирующих осей состоит
в том, что все точки фигуры движутся по окружностям в
плоскостях,перпендикулярных к оси вращения, параллельно плоскости проекций, которой перпендикулярна ось вращения.
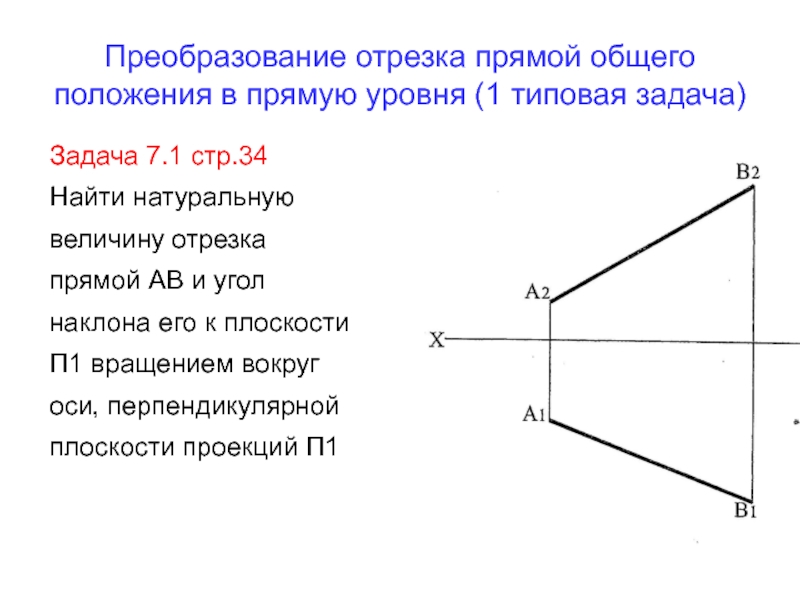
Слайд 7Преобразование отрезка прямой общего положения в прямую уровня (1 типовая
задача)
Задача 7.1 стр.34
Найти натуральную величину отрезка прямой АВ и угол
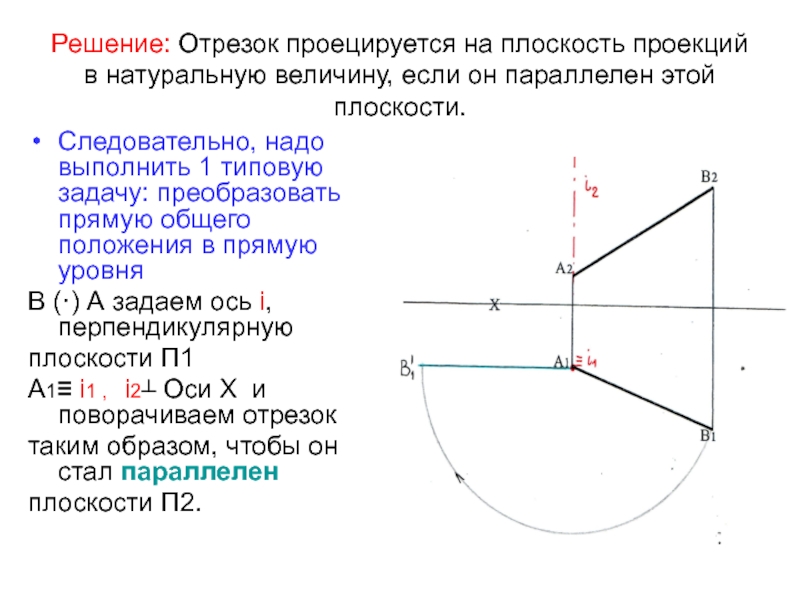
наклона его к плоскости П1 вращением вокруг оси, перпендикулярной плоскости проекций П1Слайд 8Решение: Отрезок проецируется на плоскость проекций в натуральную величину, если
он параллелен этой плоскости.
Следовательно, надо выполнить 1 типовую задачу:
преобразовать прямую общего положения в прямую уровняВ (·) А задаем ось i, перпендикулярную
плоскости П1
А1≡ i1 , i2┴ Оси Х и поворачиваем отрезок
таким образом, чтобы он стал параллелен
плоскости П2.
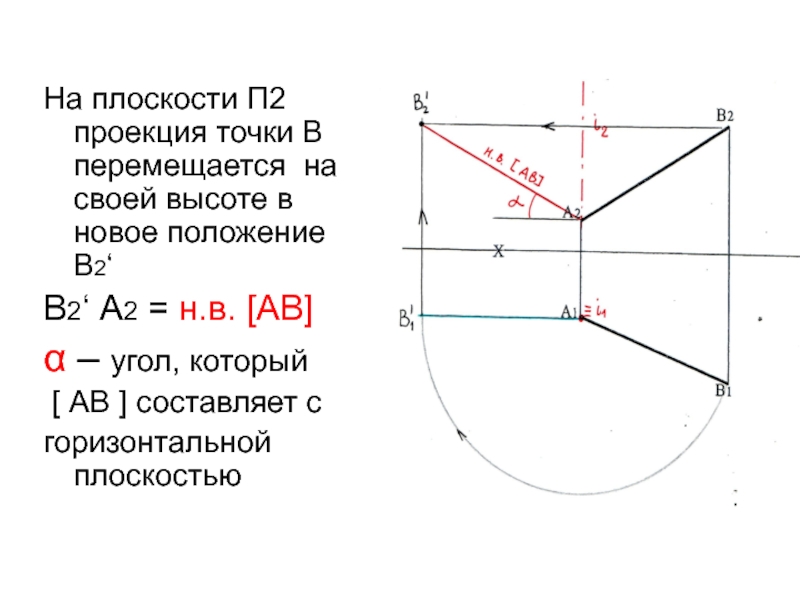
Слайд 9На плоскости П2 проекция точки В перемещается на своей высоте
в новое положение В2‘
В2‘ А2 = н.в. [АВ]
α – угол,
который[ АВ ] составляет с
горизонтальной плоскостью
Слайд 10Преобразование отрезка прямой общего положения в проецирующий (2 типовая задача)
В
том случае, если [ АВ ] – отрезок прямой
общего положения,
задача решается в два действия.
1. Преобразовываем отрезок [АВ] в прямую уровня.
2. В (·) В задаем ось j, перпендикулярную
плоскости П2 и поворачиваем отрезок
таким образом, чтобы он стал
перпендикулярен плоскости П1. Тогда он проецируется на эту плоскость в точку (В1'≡А1').
≡
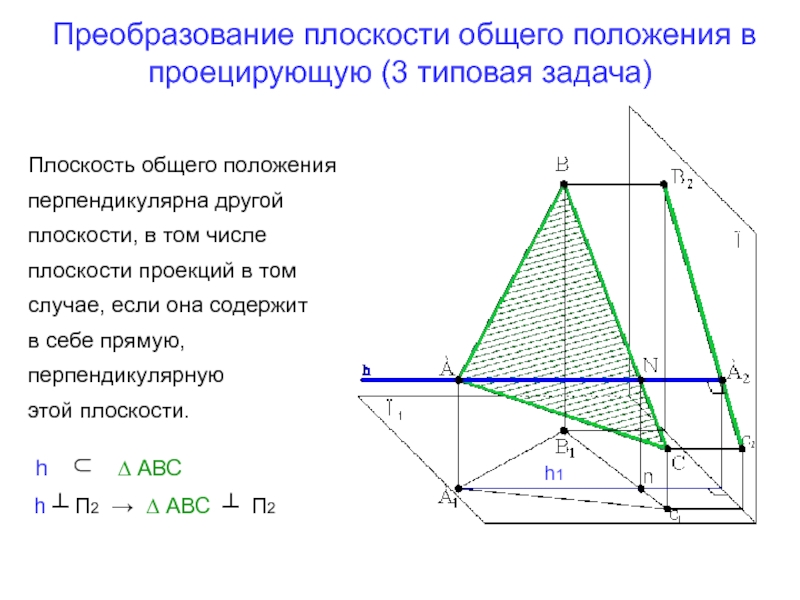
Слайд 11Преобразование плоскости общего положения в проецирующую (3 типовая задача)
Плоскость общего
положения
перпендикулярна другой
плоскости, в том числе
плоскости проекций в том
случае, если она содержит
в себе прямую,
перпендикулярную
этой плоскости.
h
∩
∆ АВС
h ┴ П2 → ∆ АВС ┴ П2
h1
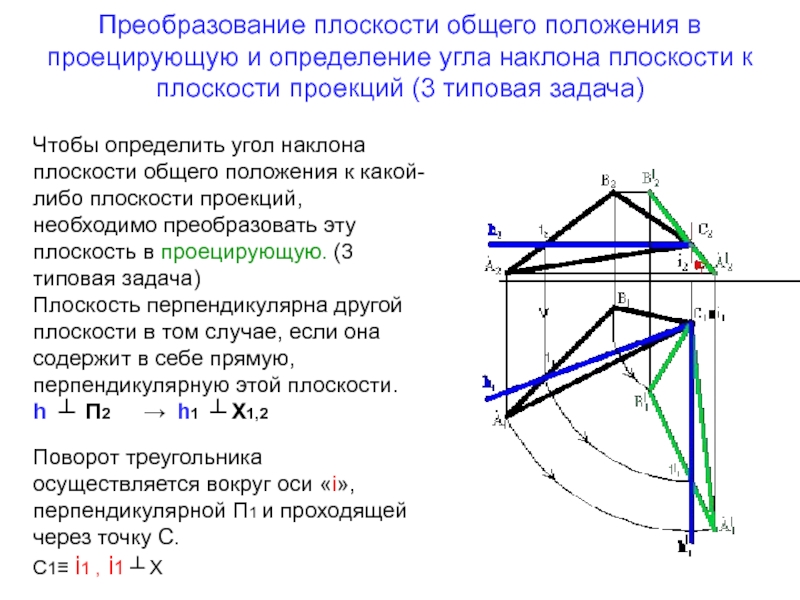
Слайд 12Преобразование плоскости общего положения в проецирующую и определение угла наклона
плоскости к плоскости проекций (3 типовая задача)
Чтобы определить угол наклона
плоскости общего положения к какой-либо плоскости проекций, необходимо преобразовать эту плоскость в проецирующую. (3 типовая задача) Плоскость перпендикулярна другой плоскости в том случае, если она содержит в себе прямую, перпендикулярную этой плоскости.
h ┴ П2 → h1 ┴ Х1,2
Поворот треугольника осуществляется вокруг оси «i», перпендикулярной П1 и проходящей через точку С.
С1≡ i1 , i1 ┴ Х
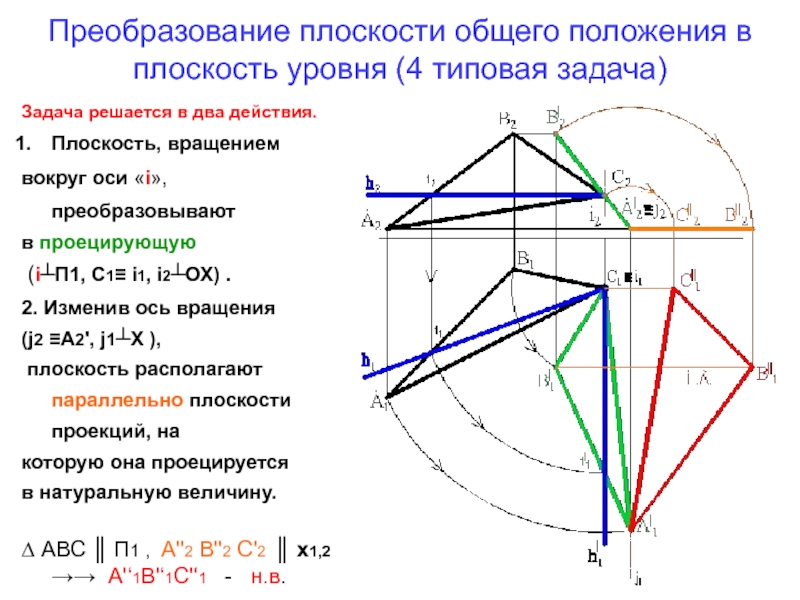
Слайд 13Преобразование плоскости общего положения в плоскость уровня (4 типовая задача)
Задача
решается в два действия.
Плоскость, вращением
вокруг оси «i», преобразовывают
в
проецирующую(i┴П1, С1≡ i1, i2┴ОХ) .
2. Изменив ось вращения
(j2 ≡A2', j1┴X ),
плоскость располагают параллельно плоскости проекций, на
которую она проецируется
в натуральную величину.
∆ АВС ║ П1 , А''2 В''2 С'2 ║ х1,2 →→ А'‘1В'‘1С'‘1 - н.в.
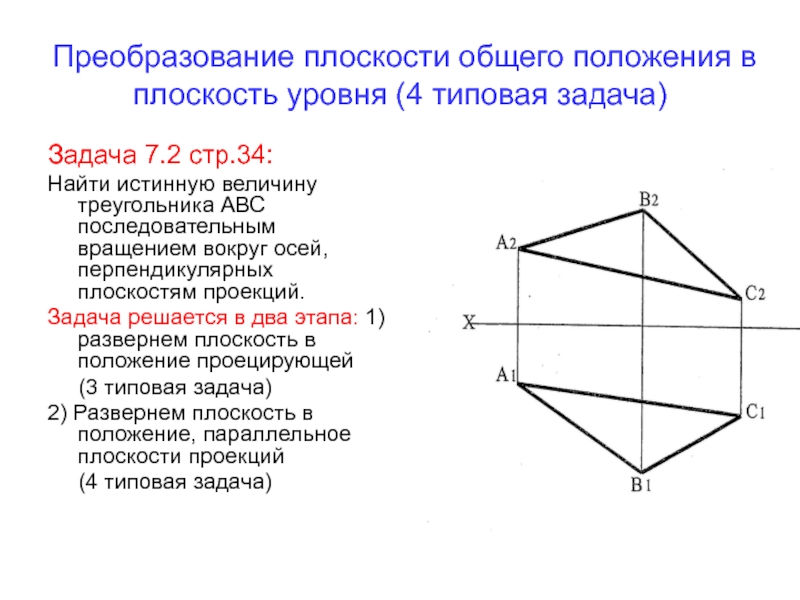
Слайд 14Преобразование плоскости общего положения в плоскость уровня (4 типовая задача)
Задача
7.2 стр.34:
Найти истинную величину треугольника АВС последовательным вращением вокруг осей,
перпендикулярных плоскостям проекций.Задача решается в два этапа: 1) развернем плоскость в положение проецирующей
(3 типовая задача)
2) Развернем плоскость в положение, параллельное плоскости проекций
(4 типовая задача)
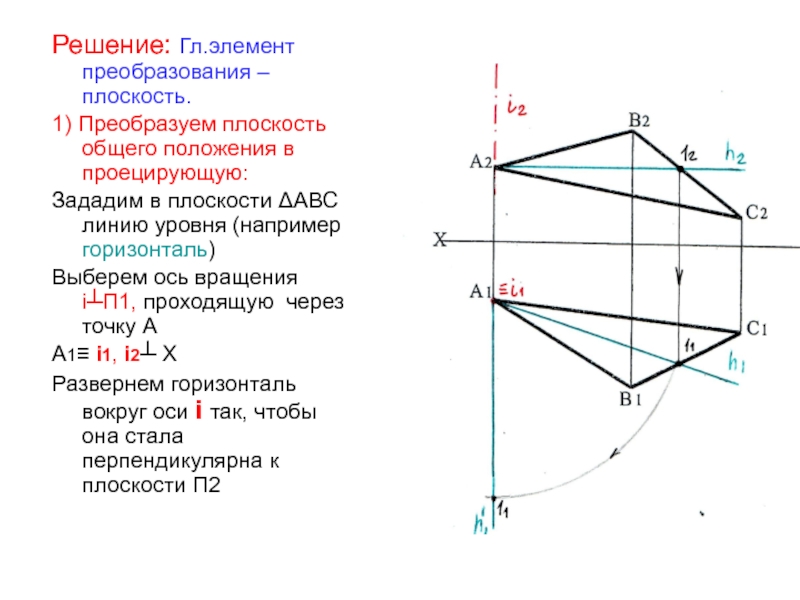
Слайд 15Решение: Гл.элемент преобразования – плоскость.
1) Преобразуем плоскость общего положения в
проецирующую:
Зададим в плоскости ΔАВС линию уровня (например горизонталь)
Выберем ось
вращения i┴П1, проходящую через точку АА1≡ i1, i2┴ Х
Развернем горизонталь вокруг оси i так, чтобы она стала перпендикулярна к плоскости П2
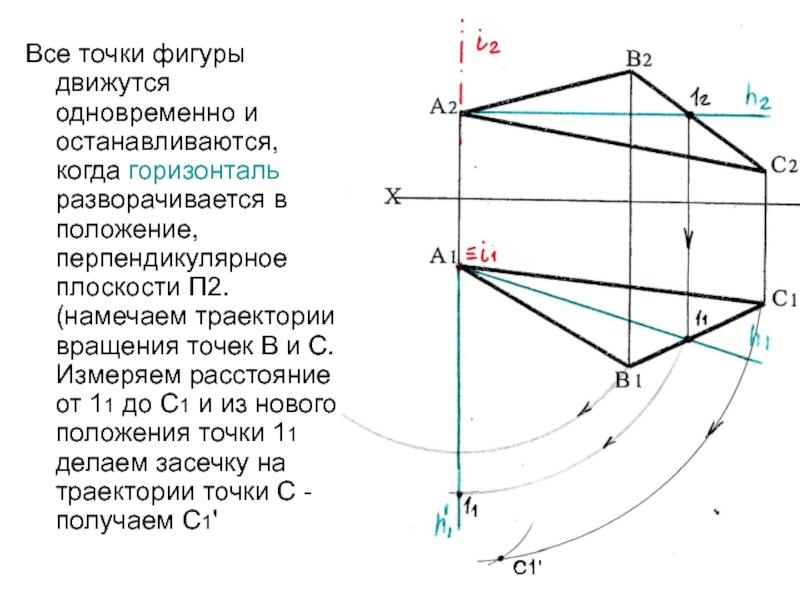
Слайд 16Все точки фигуры движутся одновременно и останавливаются, когда горизонталь разворачивается
в положение, перпендикулярное плоскости П2. (намечаем траектории вращения точек В
и С. Измеряем расстояние от 11 до С1 и из нового положения точки 11 делаем засечку на траектории точки С - получаем С1'С1'
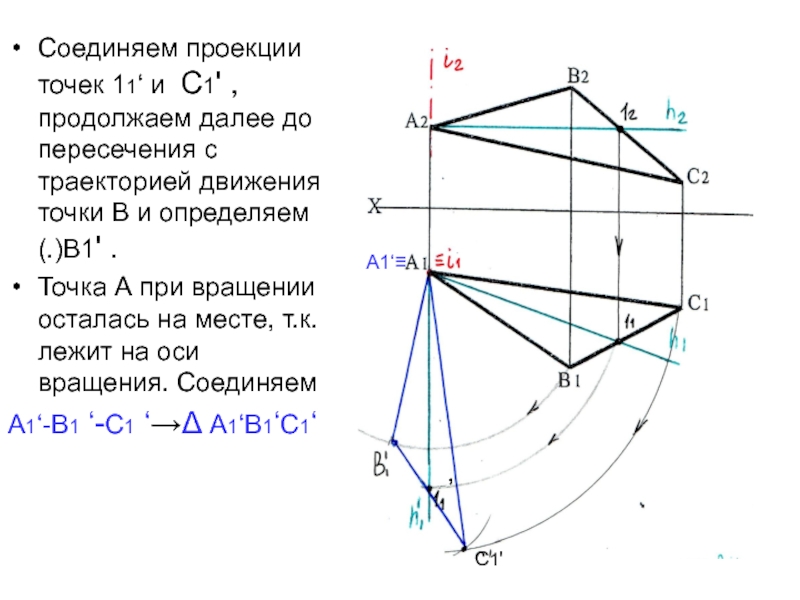
Слайд 17Соединяем проекции точек 11‘ и С1' , продолжаем далее до
пересечения с траекторией движения точки В и определяем (.)В1' .
Точка
А при вращении осталась на месте, т.к. лежит на оси вращения. Соединяем А1‘-В1 ‘-С1 ‘→Δ А1‘В1‘С1‘
С1'
‘
А1‘≡
Слайд 18
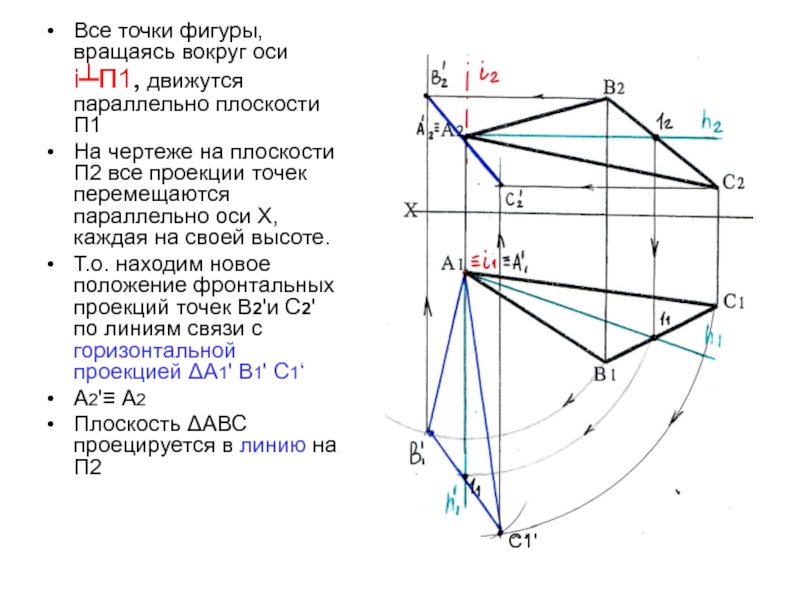
Все точки фигуры, вращаясь вокруг оси i┴П1, движутся параллельно
плоскости П1
На чертеже на плоскости П2 все проекции точек перемещаются
параллельно оси Х, каждая на своей высоте.Т.о. находим новое положение фронтальных проекций точек В2'и С2' по линиям связи с горизонтальной проекцией ΔА1' В1' С1‘
А2'≡ А2
Плоскость ΔАВС проецируется в линию на П2
С1'
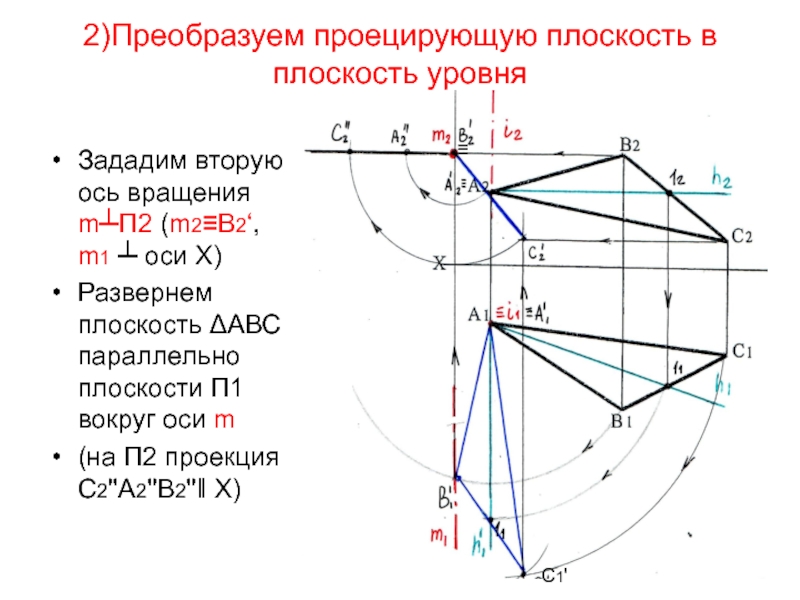
Слайд 192)Преобразуем проецирующую плоскость в плоскость уровня
Зададим вторую ось вращения m┴П2
(m2≡В2‘, m1 ┴ оси Х)
Развернем плоскость ΔАВС параллельно плоскости
П1 вокруг оси m (на П2 проекция С2''А2''В2''‖ Х)
С1'
≡
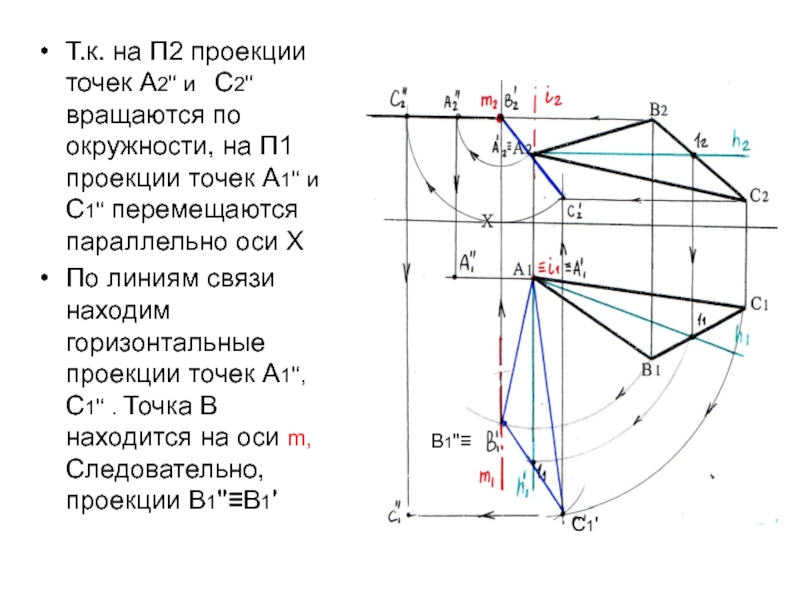
Слайд 20Т.к. на П2 проекции точек А2'‘ и С2'‘ вращаются
по окружности, на П1 проекции точек А1'‘ и С1'‘ перемещаются
параллельно оси ХПо линиям связи находим горизонтальные проекции точек А1'‘, С1'‘ . Точка В находится на оси m, Следовательно, проекции В1''≡В1'
В1''≡
С1'
Слайд 22Вращение вокруг линий уровня
Этот способ применяется для преобразования плоскости общего
положения в плоскость уровня и для определения действительной величины плоской
фигуры.Задача решается одним вращением вокруг линии уровня данной плоскости- горизонтали или фронтали.
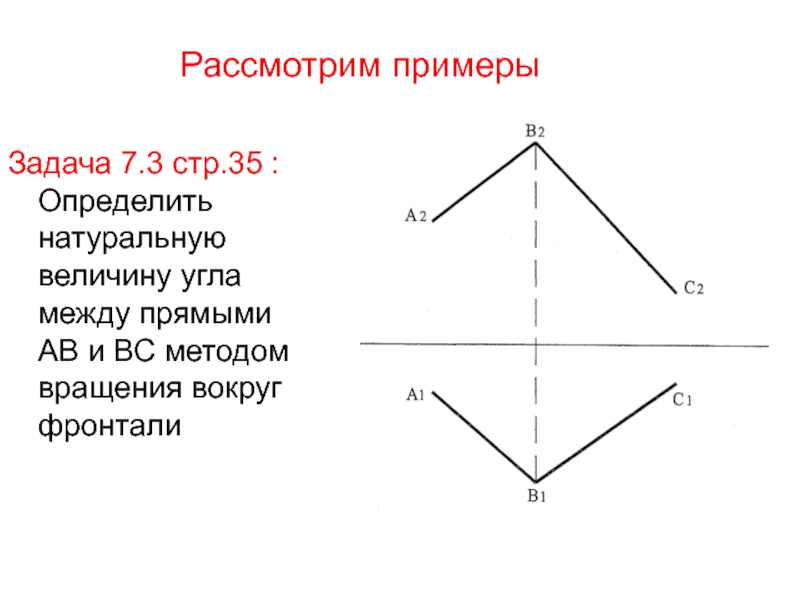
Слайд 23Рассмотрим примеры
Задача 7.3 стр.35 : Определить натуральную величину угла между
прямыми АВ и ВС методом вращения вокруг фронтали
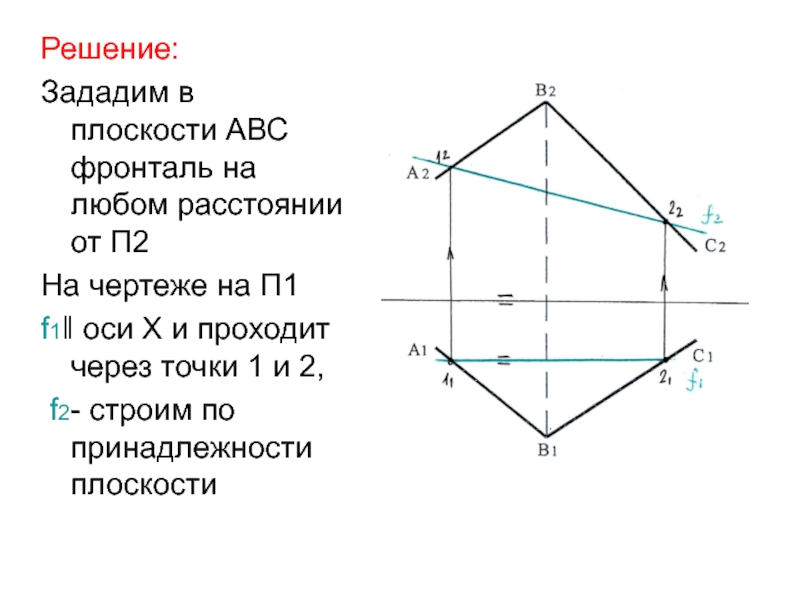
Слайд 24Решение:
Зададим в плоскости АВС фронталь на любом расстоянии от П2
На
чертеже на П1
f1‖ оси Х и проходит через точки
1 и 2, f2- строим по принадлежности плоскости
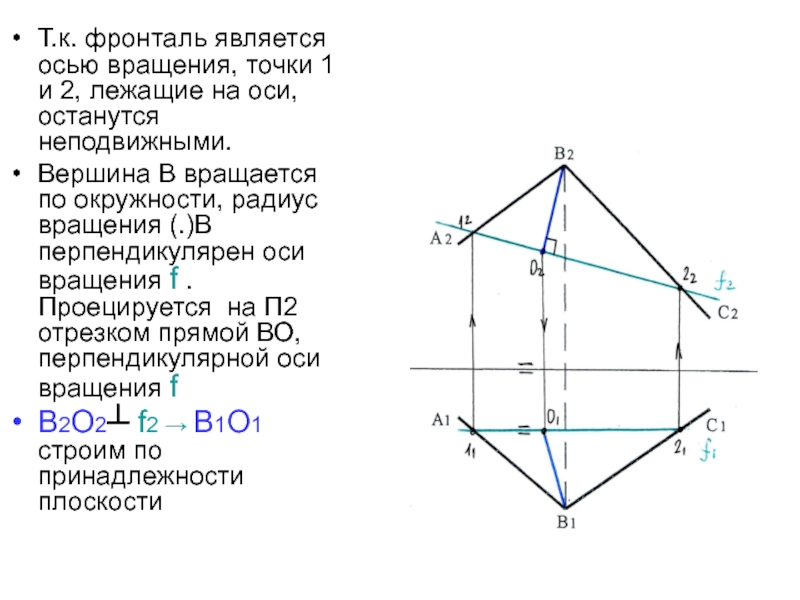
Слайд 25Т.к. фронталь является осью вращения, точки 1 и 2, лежащие
на оси, останутся неподвижными.
Вершина В вращается по окружности, радиус вращения
(.)В перпендикулярен оси вращения f . Проецируется на П2 отрезком прямой ВО, перпендикулярной оси вращения fВ2О2┴ f2 → В1О1 строим по принадлежности плоскости
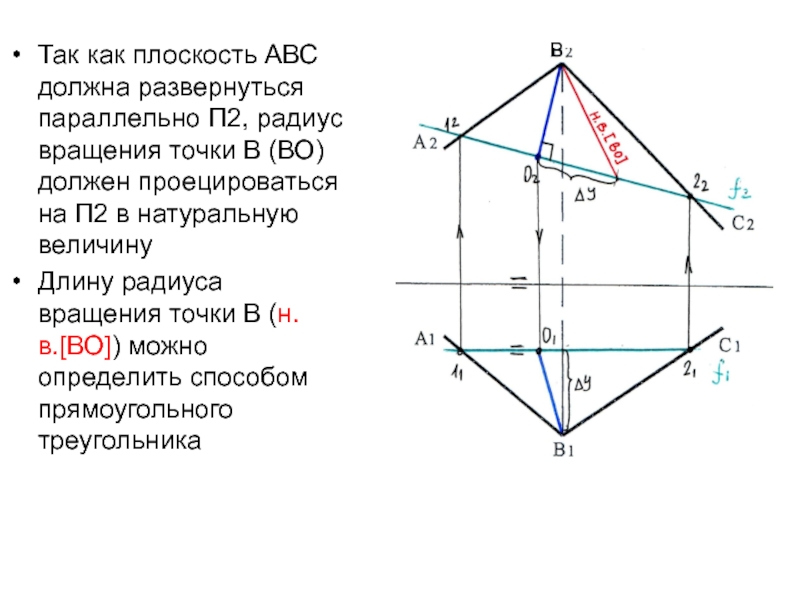
Слайд 26Так как плоскость АВС должна развернуться параллельно П2, радиус вращения
точки В (ВО) должен проецироваться на П2 в натуральную величину
Длину
радиуса вращения точки В (н.в.[ВО]) можно определить способом прямоугольного треугольникаВ
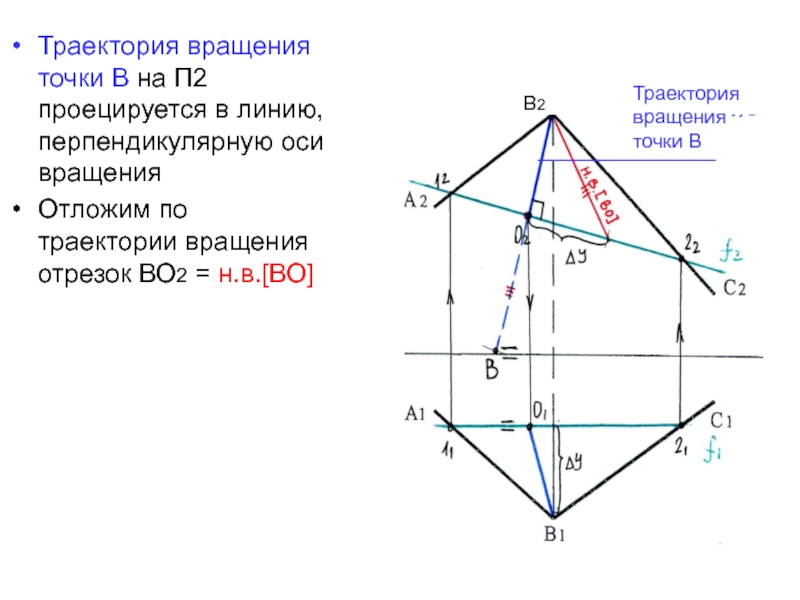
Слайд 27Траектория вращения точки В на П2 проецируется в линию, перпендикулярную
оси вращения
Отложим по траектории вращения отрезок ВО2 = н.в.[ВО]
Траектория вращения
точки ВВ2
________________
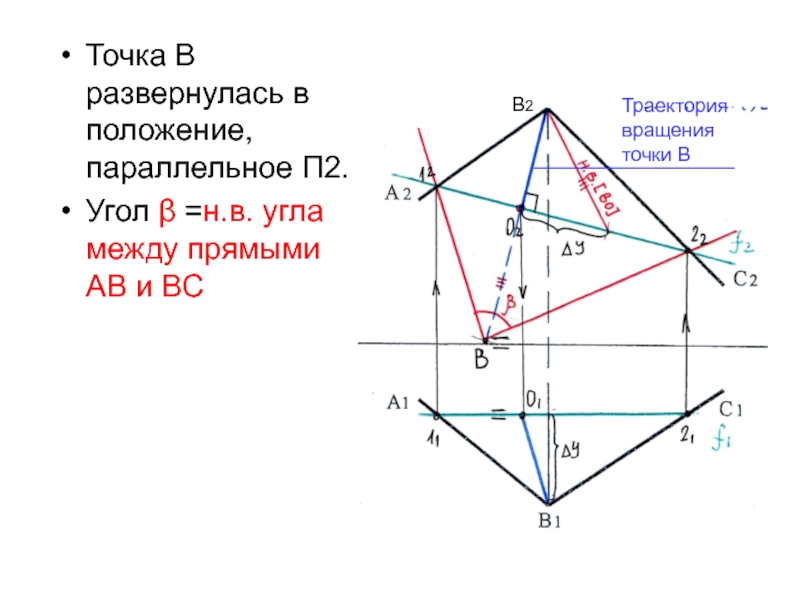
Слайд 28Точка В развернулась в положение, параллельное П2.
Угол β =н.в. угла
между прямыми АВ и ВС
В2
Траектория вращения точки В
__________________
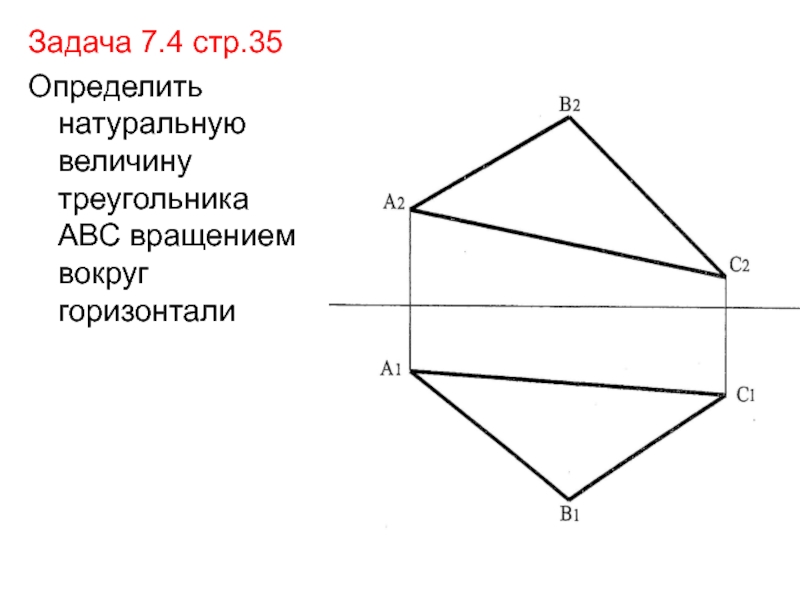
Слайд 29Задача 7.4 стр.35
Определить натуральную величину треугольника АВС вращением вокруг горизонтали
Слайд 30Решение:
Зададим в плоскости АВС горизонталь на любой высоте от П1
(например, через (.)А
На чертеже на П2
h2‖ оси Х и
проходит через точки 1 и А, h1- строим по принадлежности плоскости
Слайд 31Т.к. горизонталь является осью вращения, точки 1 и А, лежащие
на оси, останутся неподвижными.
Вершины В и С вращаются по окружностям.
Радиусы вращения точек В и С проецируются на П1 отрезками прямых В1О1 и С1К1 , перпендикулярными горизонтальной проекции оси вращения h1 (на основании теоремы о проецировании прямого угла без искажения)В1О1┴ h1,
С1К1┴ h1
Слайд 33Так как плоскость АВС должна развернуться параллельно П1, радиусы вращения
точек В (ВО) и С (СК) должны проецироваться на П1
в натуральную величинуДлины радиусов вращения точек В (н.в.[ВО]) и С (н.в.[СК]) можно определить способом прямоугольного треугольника
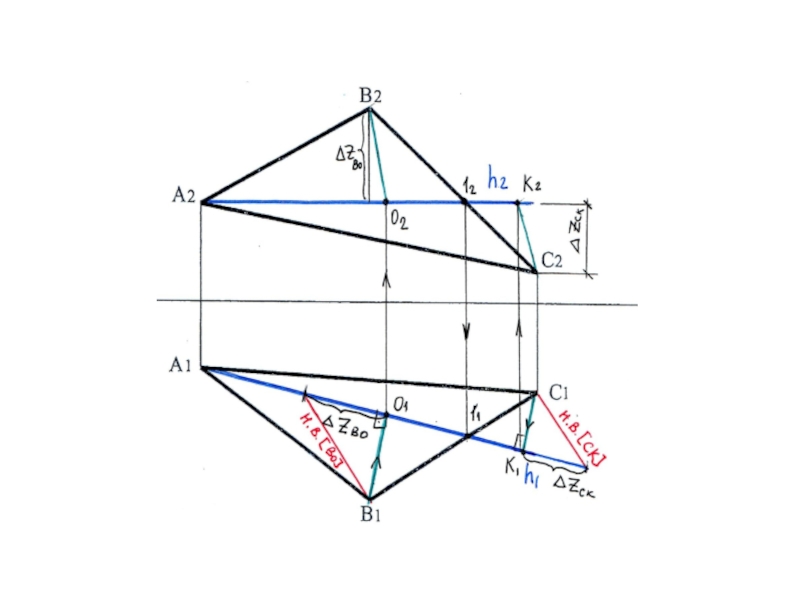
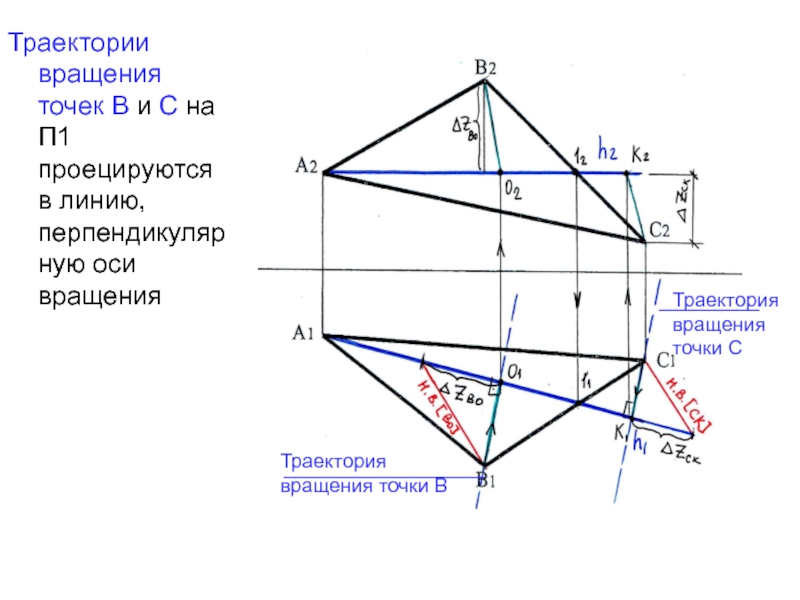
Слайд 35Траектория вращения точки В
Траектория вращения точки С
_________
__________________
Траектории вращения точек В
и С на П1 проецируются в линию, перпендикулярную оси вращения
Слайд 36Отложим по траектории вращения точки В отрезок ВО1 = н.в.[ВО]
и по траектории вращения точки С
отрезок СК1 = н.в.[СК]
Соединив
проекции А1, В,С получимнатуральную величину ΔАВС
Траектория вращения точки В
________________
_______
Траектория вращения
точки С
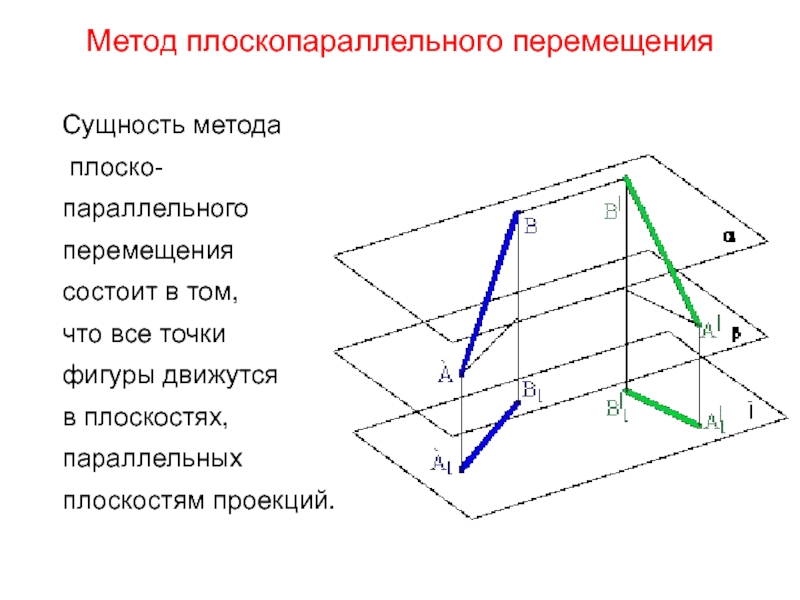
Слайд 37Метод плоскопараллельного перемещения
Сущность метода
плоско-
параллельного
перемещения
состоит в том,
что все
точки
фигуры движутся
в плоскостях,
параллельных
плоскостям проекций.
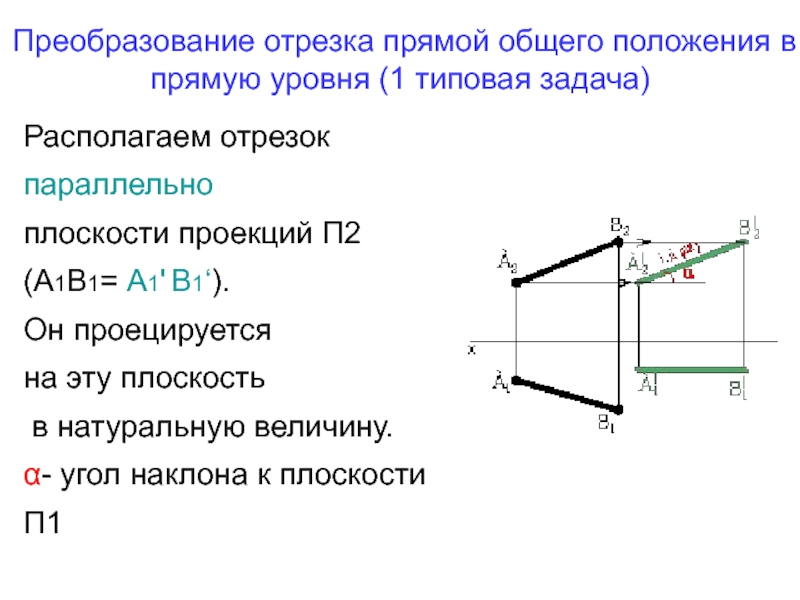
Слайд 38Преобразование отрезка прямой общего положения в прямую уровня (1 типовая
задача)
Располагаем отрезок
параллельно
плоскости проекций П2
(А1В1= А1' В1‘).
Он
проецируетсяна эту плоскость
в натуральную величину.
α- угол наклона к плоскости П1
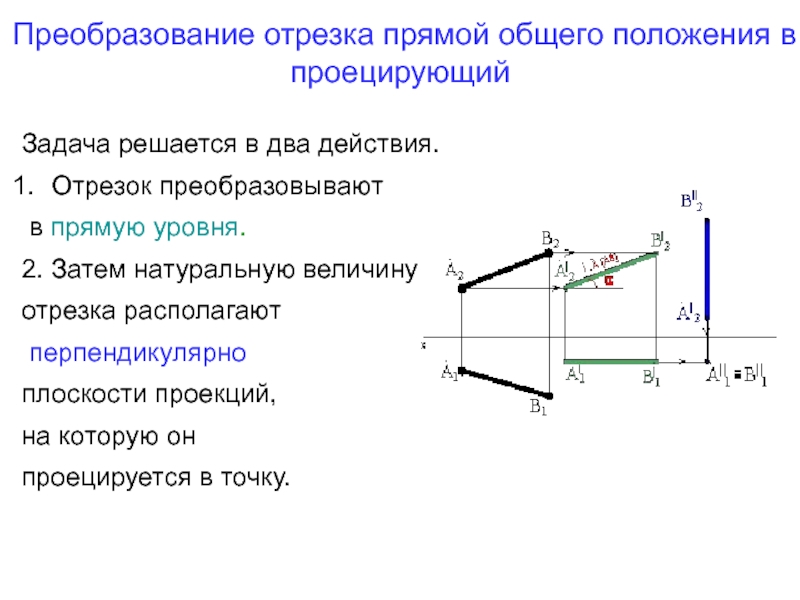
Слайд 39Преобразование отрезка прямой общего положения в проецирующий
Задача решается в два
действия.
Отрезок преобразовывают
в прямую уровня.
2. Затем натуральную величину
отрезка располагают
перпендикулярноплоскости проекций,
на которую он
проецируется в точку.
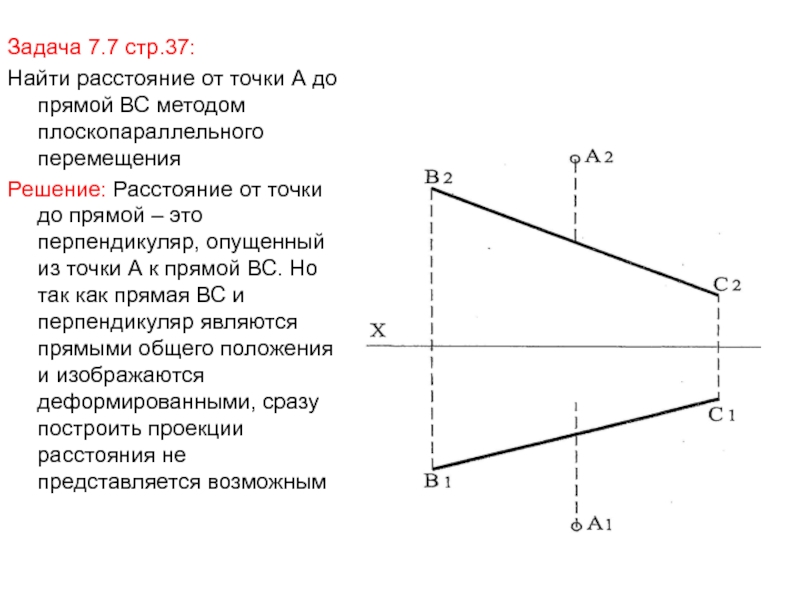
Слайд 40Задача 7.7 стр.37:
Найти расстояние от точки А до прямой ВС
методом плоскопараллельного перемещения
Решение: Расстояние от точки до прямой – это
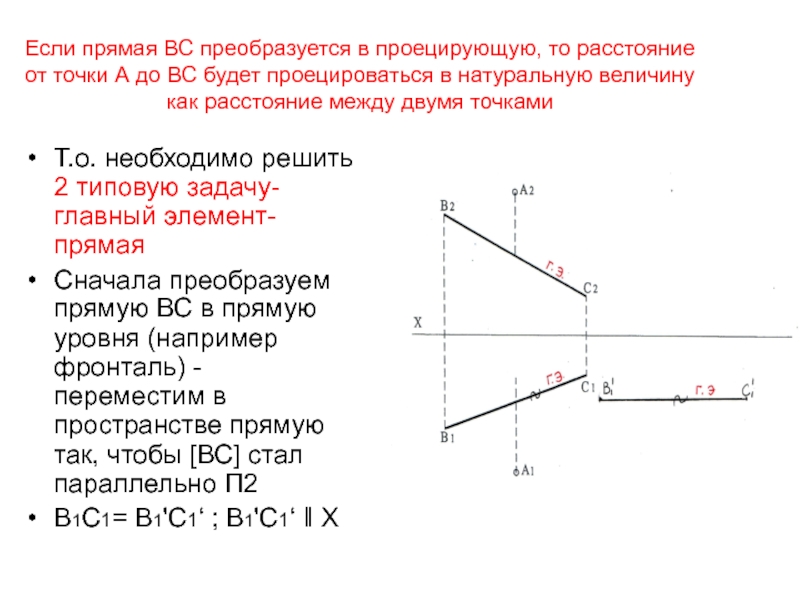
перпендикуляр, опущенный из точки А к прямой ВС. Но так как прямая ВС и перпендикуляр являются прямыми общего положения и изображаются деформированными, сразу построить проекции расстояния не представляется возможным Слайд 41Если прямая ВС преобразуется в проецирующую, то расстояние от точки
А до ВС будет проецироваться в натуральную величину как расстояние
между двумя точкамиТ.о. необходимо решить 2 типовую задачу- главный элемент- прямая
Сначала преобразуем прямую ВС в прямую уровня (например фронталь) - переместим в пространстве прямую так, чтобы [ВС] стал параллельно П2
В1С1= В1'С1‘ ; В1'С1‘ ‖ Х
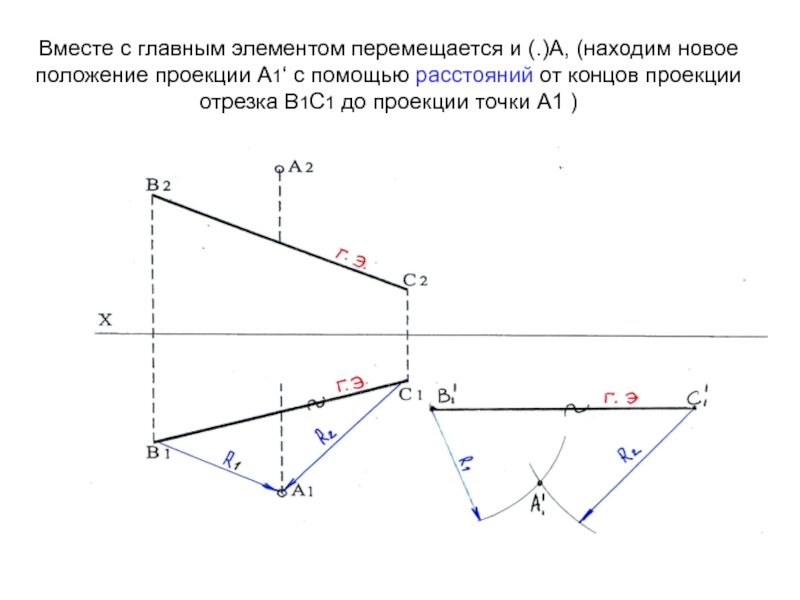
Слайд 42Вместе с главным элементом перемещается и (.)А, (находим новое положение
проекции А1‘ с помощью расстояний от концов проекции отрезка В1С1
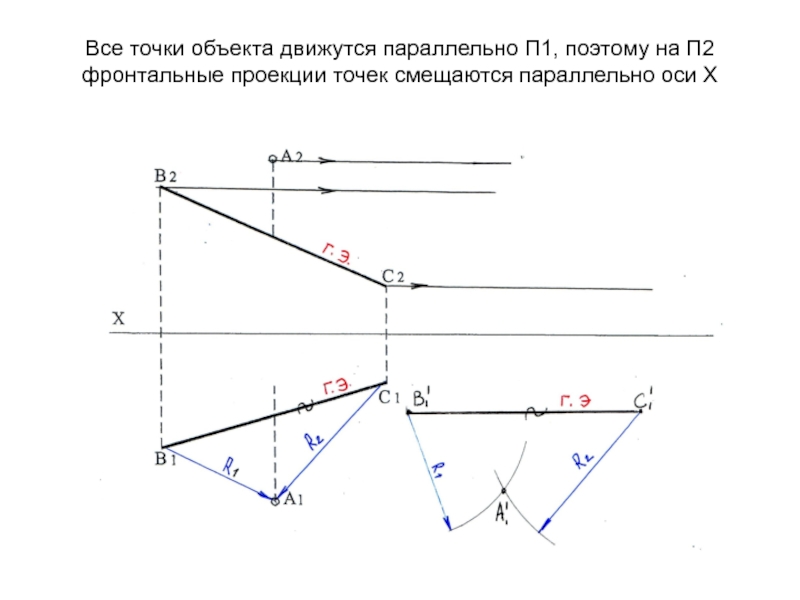
до проекции точки А1 )Слайд 43Все точки объекта движутся параллельно П1, поэтому на П2 фронтальные
проекции точек смещаются параллельно оси Х
Слайд 46Преобразуем главный элемент- отрезок прямой ВС в положение проецирующего. На
чертеже н.в. [ВС] = В2‘С2' располагаем перпендикулярно оси Х →
В2‘‘С2'‘ и вместе с ней переносим проекцию точки А2‘‘, измеряя расстояния с предыдущей проекции (R1,R2)С '‘
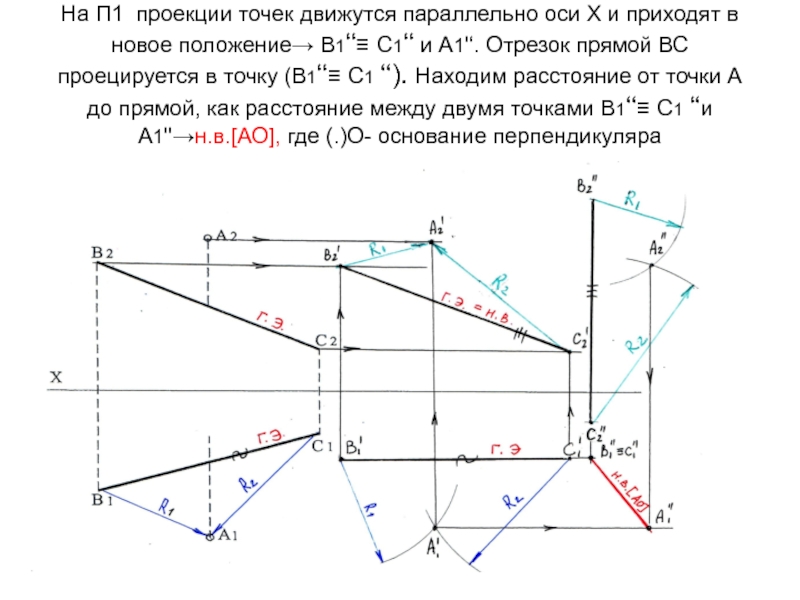
Слайд 47На П1 проекции точек движутся параллельно оси Х и приходят
в новое положение→ В1‘‘≡ С1‘‘ и А1'‘. Отрезок прямой ВС
проецируется в точку (В1‘‘≡ С1 ‘‘). Находим расстояние от точки А до прямой, как расстояние между двумя точками В1‘‘≡ С1 ‘‘и А1''→н.в.[АО], где (.)О- основание перпендикуляраСлайд 48Находим недостающую проекцию АО на П2. Т.к. на П1 отрезок
проецируется как н.в.[АО], на П2 его фронтальная проекция параллельна оси
Х.Слайд 49Далее покажем, как выглядят проекции АО на исходных данных. Для
этого измерим А2''О2'‘(выделен желтым цветом) и вернем на предыдущее положение
(на первое перемещение). Получим А2'О2'Слайд 50По линиям связи определим горизонтальную проекцию О1‘ и, соединив с
А1‘, получим горизонтальную проекцию О1‘А1‘ на проекциях после первого перемещения
Слайд 51Далее по линиям связи найдем проекции О2 (параллельно оси Х
на высоте точки О) и О1 на П1. Соединив одноименные
проекции, получим проекции кратчайшего расстояния от точки до прямой на исходных изображениях (А2О2 и А1О1 - выделены желтым цветом)Слайд 52Второй вариант возврата точки О на исходные проекции: измеряем расстояние
а на горизонтальной проекции В1‘С1 ‘ на промежуточном положении прямой
и переносим на исходную горизонтальную проекцию В1С1, получаем (.)О1. Потом находим О2 по линии связиСлайд 53Определение расстояния между параллельными прямыми способом плоскопараллельного перемещения
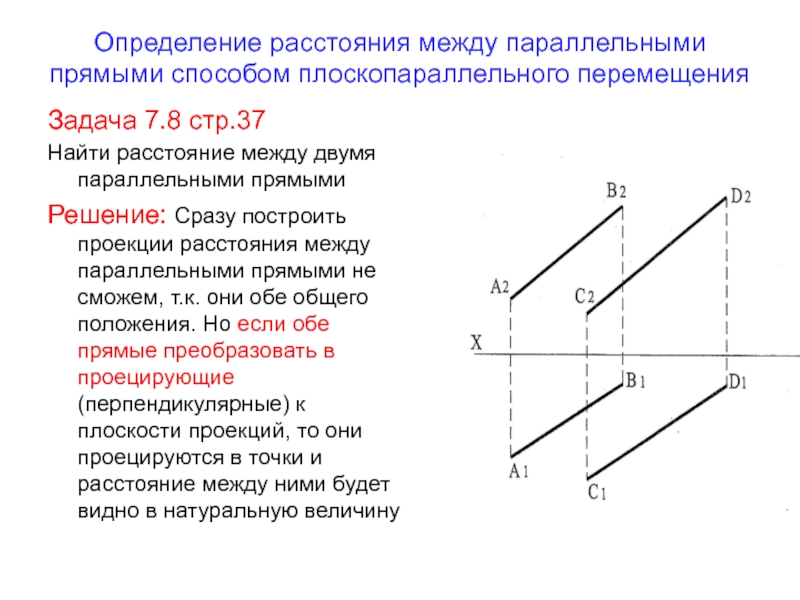
Задача 7.8 стр.37
Найти
расстояние между двумя параллельными прямыми
Решение: Сразу построить проекции расстояния между
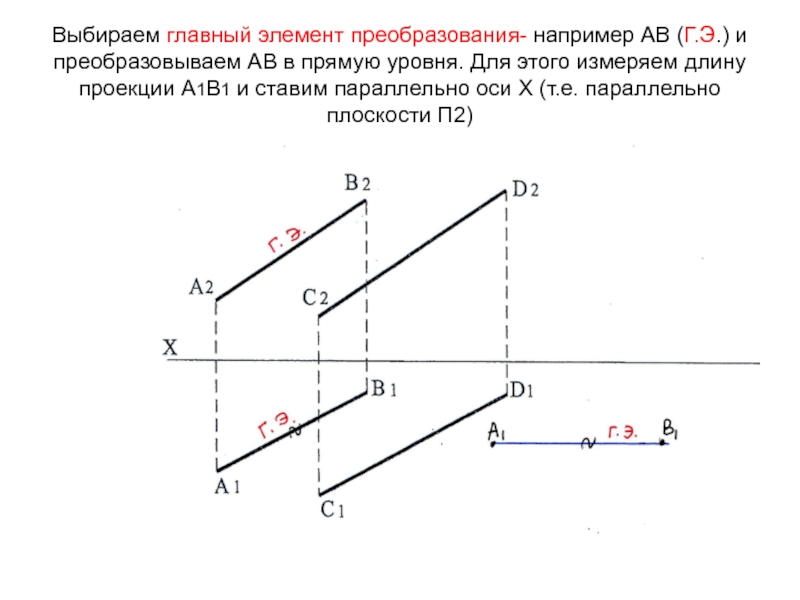
параллельными прямыми не сможем, т.к. они обе общего положения. Но если обе прямые преобразовать в проецирующие (перпендикулярные) к плоскости проекций, то они проецируются в точки и расстояние между ними будет видно в натуральную величинуСлайд 54Выбираем главный элемент преобразования- например АВ (Г.Э.) и преобразовываем АВ
в прямую уровня. Для этого измеряем длину проекции А1В1 и
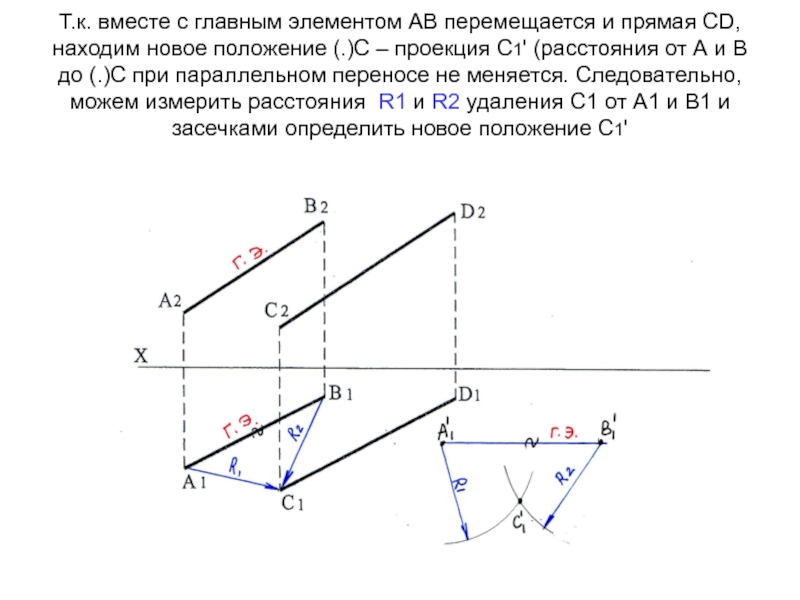
ставим параллельно оси Х (т.е. параллельно плоскости П2)Слайд 55Т.к. вместе с главным элементом АВ перемещается и прямая СD,
находим новое положение (.)С – проекция С1' (расстояния от А
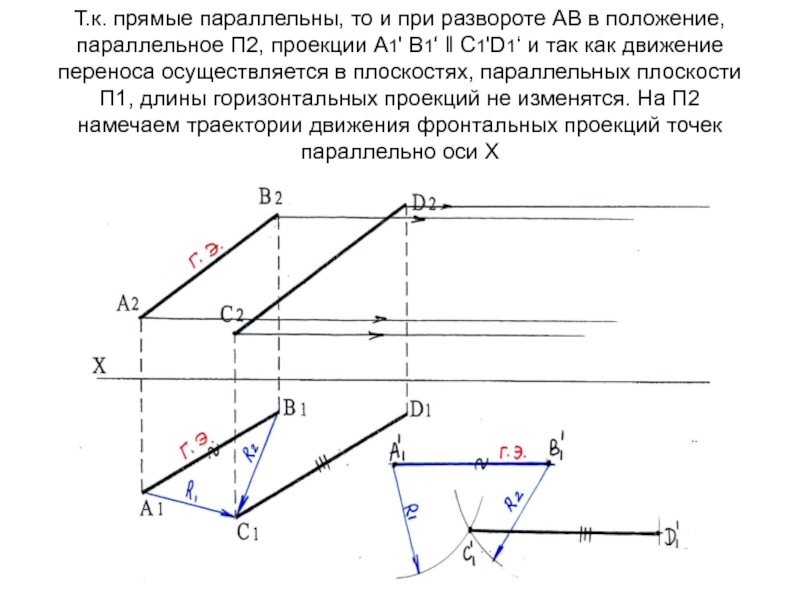
и В до (.)С при параллельном переносе не меняется. Следовательно, можем измерить расстояния R1 и R2 удаления С1 от А1 и В1 и засечками определить новое положение С1'Слайд 56Т.к. прямые параллельны, то и при развороте АВ в положение,
параллельное П2, проекции А1' В1‘ ‖ С1'D1‘ и так как
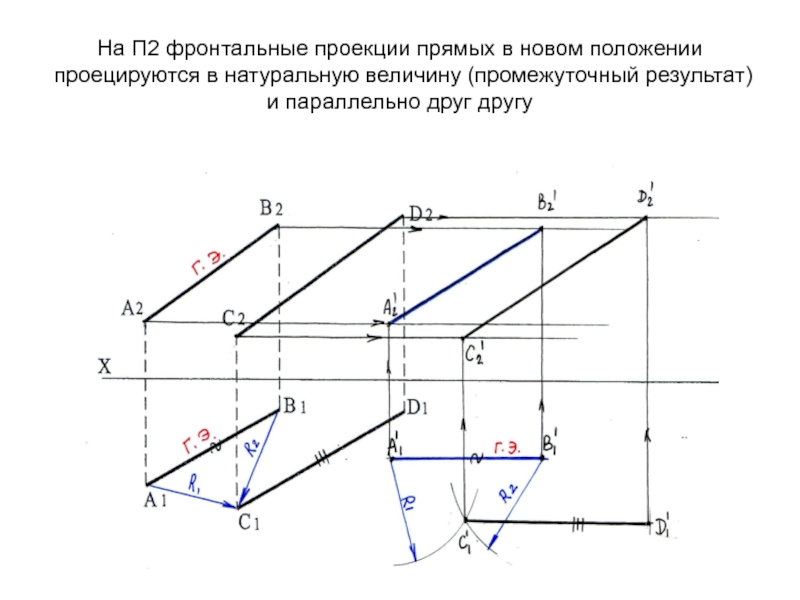
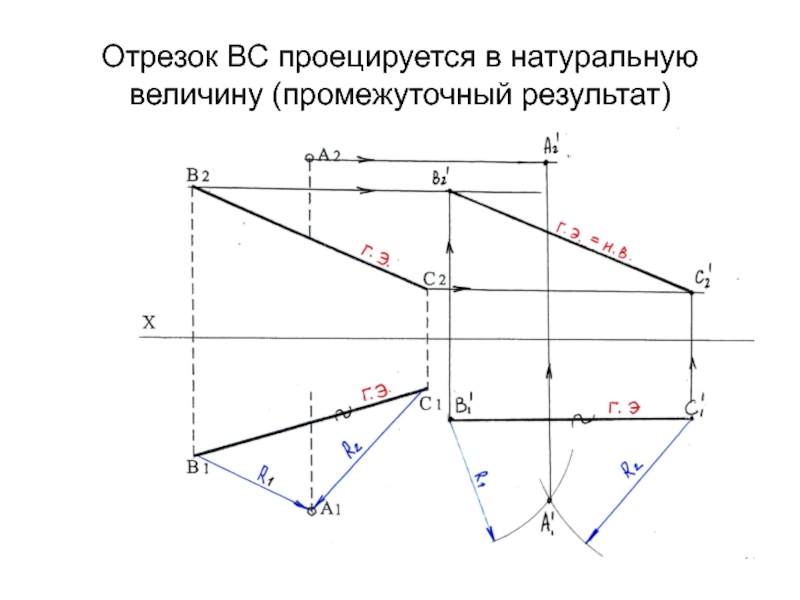
движение переноса осуществляется в плоскостях, параллельных плоскости П1, длины горизонтальных проекций не изменятся. На П2 намечаем траектории движения фронтальных проекций точек параллельно оси ХСлайд 58На П2 фронтальные проекции прямых в новом положении проецируются в
натуральную величину (промежуточный результат) и параллельно друг другу
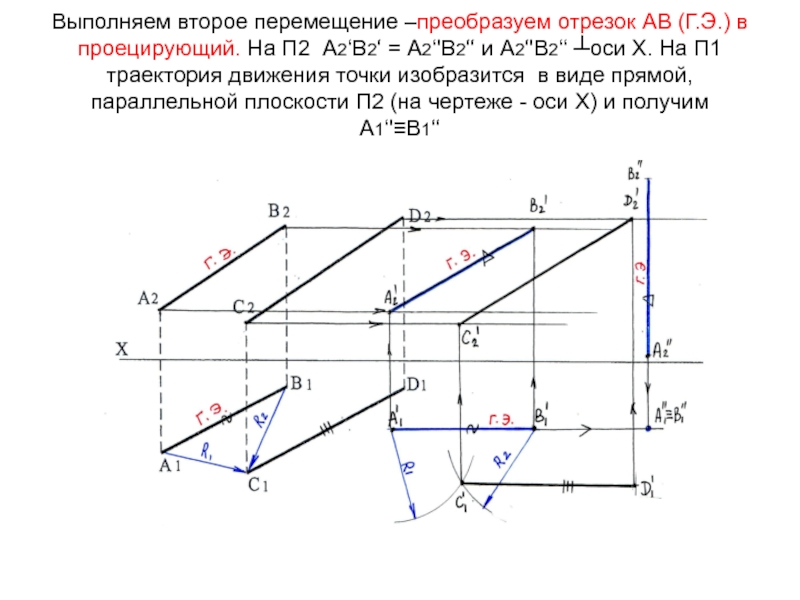
Слайд 59Выполняем второе перемещение –преобразуем отрезок АВ (Г.Э.) в проецирующий. На
П2 А2‘В2‘ = А2‘'В2‘‘ и А2‘'В2‘‘ ┴оси Х. На П1
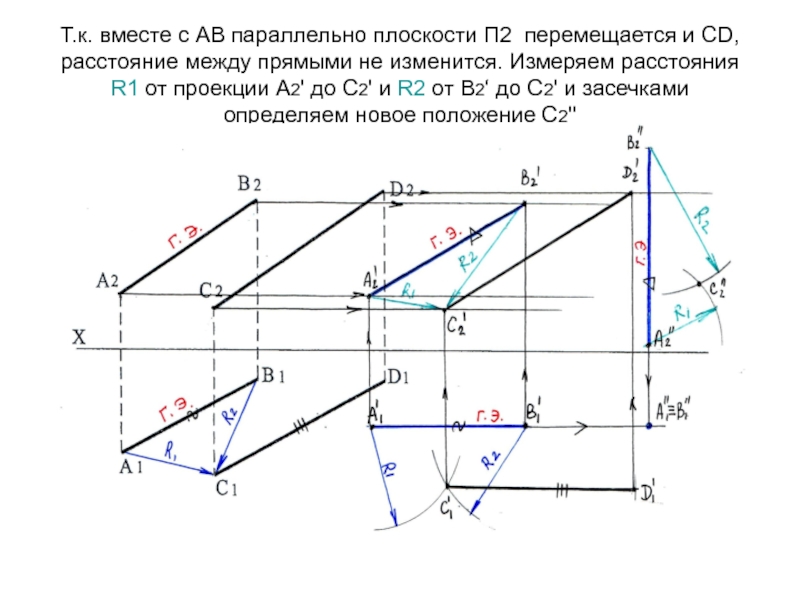
траектория движения точки изобразится в виде прямой, параллельной плоскости П2 (на чертеже - оси Х) и получим А1‘'≡В1‘‘Слайд 60Т.к. вместе с АВ параллельно плоскости П2 перемещается и СD,
расстояние между прямыми не изменится. Измеряем расстояния R1 от проекции
А2' до С2' и R2 от В2‘ до С2' и засечками определяем новое положение С2''Слайд 61Строим фронтальную проекцию С2'‘D2'‘ после второго перемещения (С2'D2' = С2'‘D2'‘).
Находим горизонтальную проекцию С1'‘D1'‘ . Прямая СD также проецируется в
точку (С1'‘≡ С2'‘D2'‘ 1'‘ )'‘
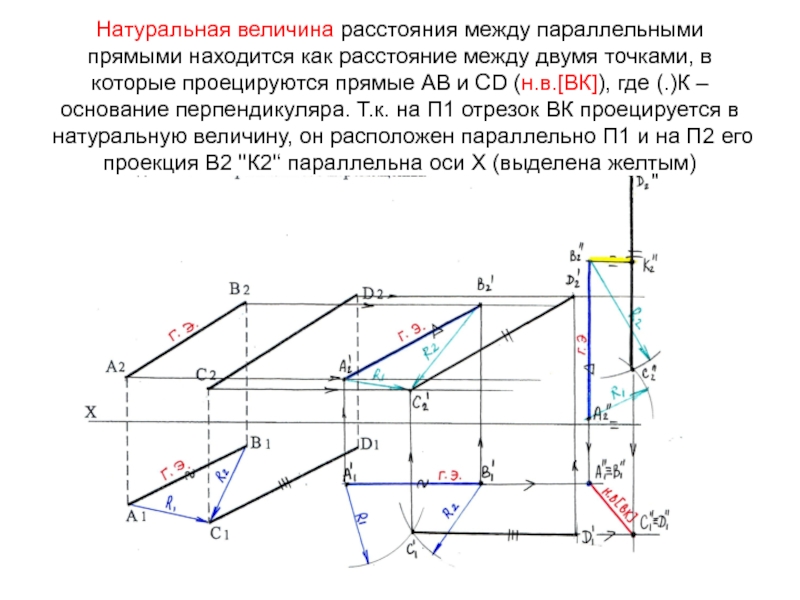
Слайд 62Натуральная величина расстояния между параллельными прямыми находится как расстояние между
двумя точками, в которые проецируются прямые АВ и СD (н.в.[ВК]),
где (.)К – основание перпендикуляра. Т.к. на П1 отрезок ВК проецируется в натуральную величину, он расположен параллельно П1 и на П2 его проекция В2 ''К2'‘ параллельна оси Х (выделена желтым)''
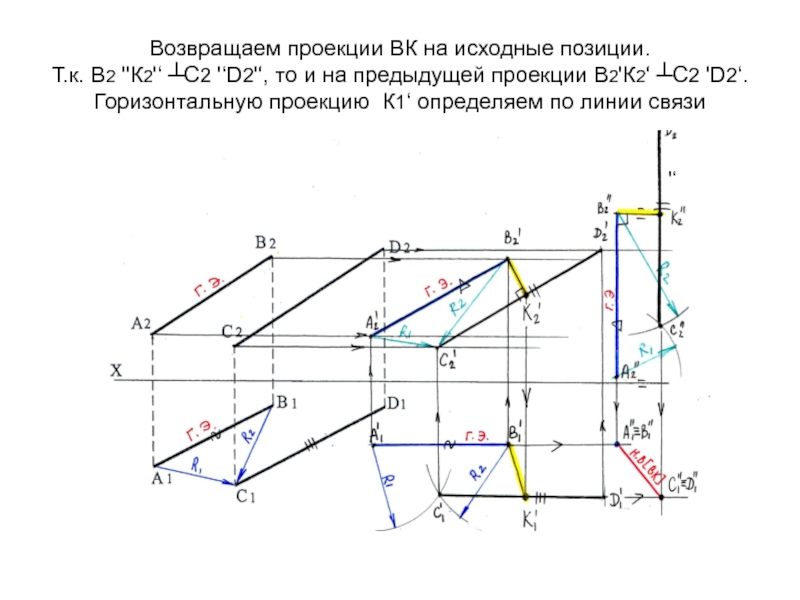
Слайд 63Возвращаем проекции ВК на исходные позиции. Т.к. В2 ''К2'‘ ┴С2
'‘D2'‘, то и на предыдущей проекции В2'К2‘ ┴С2 'D2‘. Горизонтальную
проекцию К1‘ определяем по линии связи'‘
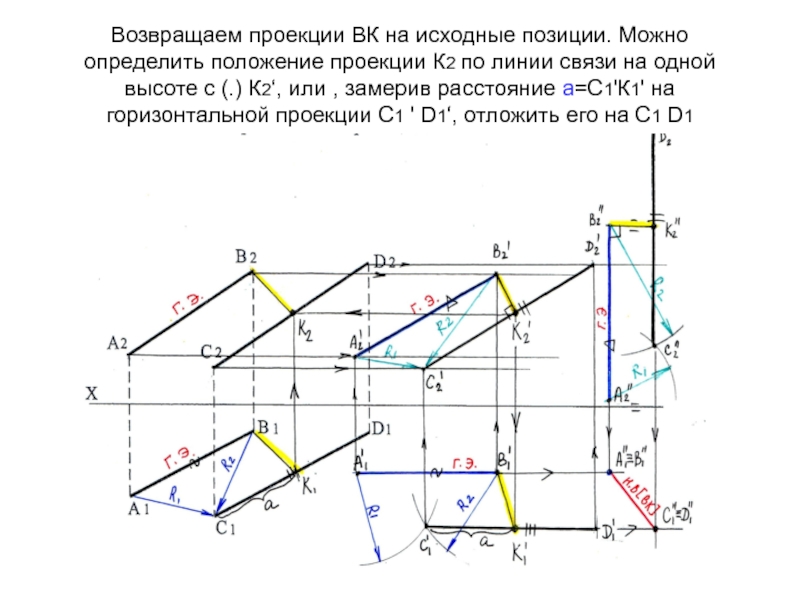
Слайд 64Возвращаем проекции ВК на исходные позиции. Можно определить положение проекции
К2 по линии связи на одной высоте с (.) К2‘,
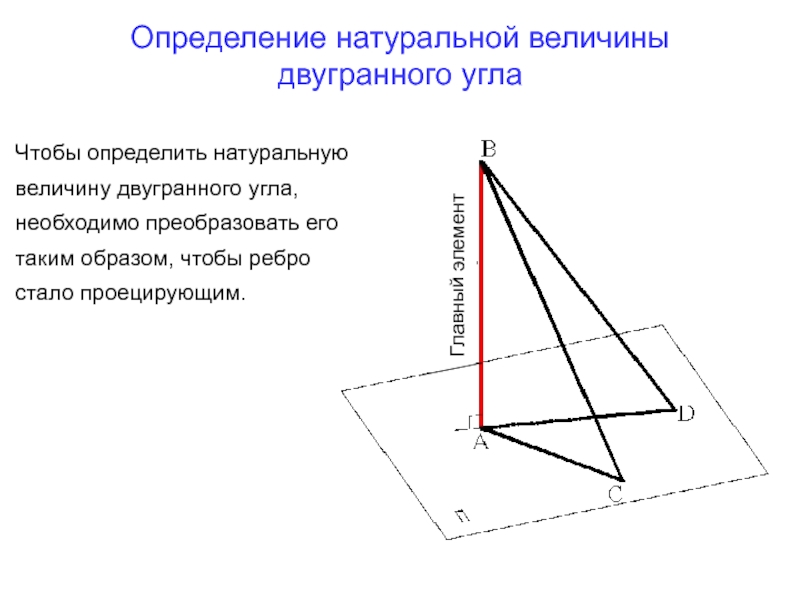
или , замерив расстояние а=С1'К1' на горизонтальной проекции С1 ' D1‘, отложить его на С1 D1Слайд 65Определение натуральной величины
двугранного угла
Главный элемент
Чтобы определить натуральную
величину двугранного
угла,
необходимо преобразовать его
таким образом, чтобы ребро
стало проецирующим.
Слайд 66Задача 7.9 стр.38 Найти истинную величину двугранного угла методом плоскопараллельного
перемещения
Решение: У двух пересекающихся плоскостей есть общее ребро ВD, которое
является прямой общего положения. Если оно преобразуется в проецирующую прямую и отразится на плоскость проекций в точку, плоскости треугольников станут проецирующими и отобразятся на данной плоскости проекций в виде линий. Плоский угол между ними будет равен пространственному углу между этими плоскостямиСлайд 67Таким образом, ВD – главный элемент (Г.Э.). 1) Преобразуем ВD
в линию уровня (1 типовая задача). Точки В и D
движутся одновременно в плоскостях, параллельных плоскости П2, поэтому на стене изображение ребра не меняется, но разворачивается в положение, параллельное плоскости П1(В2 D2 = В2' D2‘ ; В2'D2' ‖ оси Х).
На П1 траектории точек –прямые, параллельные оси Х
Находим горизонтальную проекцию ребра В1'D1‘ по линиям связи на траекториях движения точек
Слайд 68Вместе с главным элементом одновременно перемещаются точки А и С.
Измеряем расстояния от точек В2 и D2 до А2 и
засечками определяем новое положение проекции А2‘. Аналогично ищем С2'Слайд 69Соединив полученные точки, получим фронтальную проекцию двугранного угла в новом
положении. На П1 траектории движения точек А и С параллельны
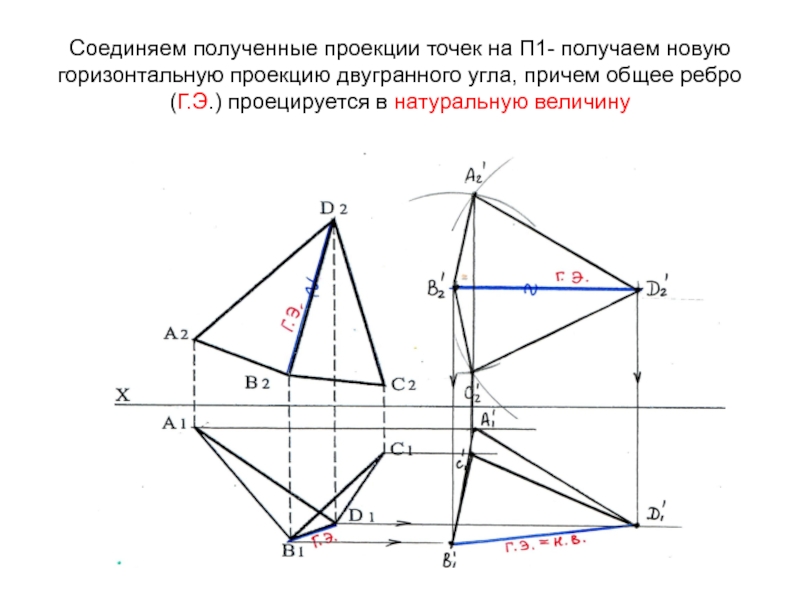
оси Х. По линиям связи определяем положение новых проекций А1' и С1'Слайд 70Соединяем полученные проекции точек на П1- получаем новую горизонтальную проекцию
двугранного угла, причем общее ребро(Г.Э.) проецируется в натуральную величину
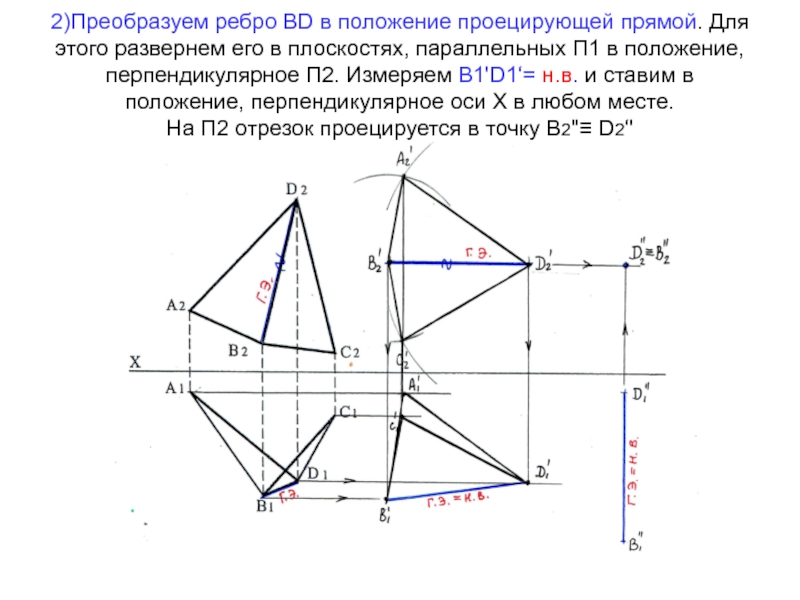
Слайд 712)Преобразуем ребро ВD в положение проецирующей прямой. Для этого развернем
его в плоскостях, параллельных П1 в положение, перпендикулярное П2. Измеряем
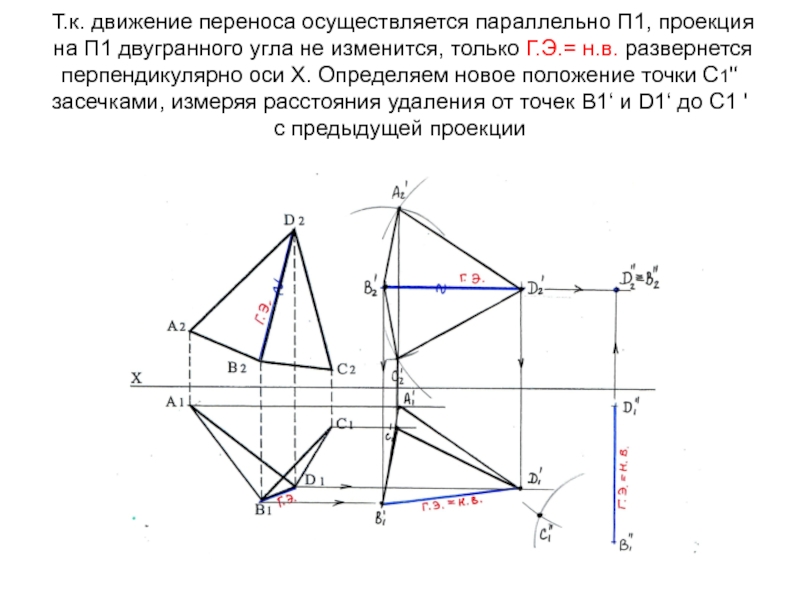
В1'D1‘= н.в. и ставим в положение, перпендикулярное оси Х в любом месте. На П2 отрезок проецируется в точку В2''≡ D2‘'Слайд 72Т.к. движение переноса осуществляется параллельно П1, проекция на П1 двугранного
угла не изменится, только Г.Э.= н.в. развернется перпендикулярно оси Х.
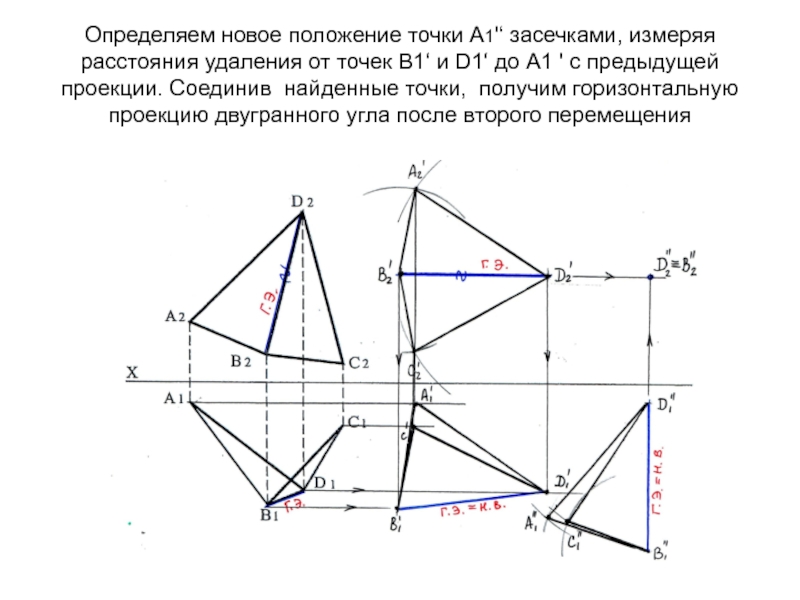
Определяем новое положение точки С1'‘ засечками, измеряя расстояния удаления от точек В1‘ и D1‘ до С1 ' с предыдущей проекцииСлайд 73Определяем новое положение точки А1'‘ засечками, измеряя расстояния удаления от
точек В1‘ и D1‘ до А1 ' с предыдущей проекции.
Соединив найденные точки, получим горизонтальную проекцию двугранного угла после второго перемещенияСлайд 74На П2 траектории движения точек параллельны оси Х. По линиям
связи определяем фронтальные проекции точек А2'‘ и С2'‘ . Получим
н.в. углаСлайд 75Определение расстояния между двумя скрещивающимися прямыми
Г.Э.
Чтобы определить расстояние
между двумя
скрещивающимися
прямыми, необходимо одну из прямых
выбрать в качестве главного элемента
и
преобразовать ее в точку. Расстояние от точки до второй
прямой и будет расстоянием
между двумя скрещиваю-
щимися прямыми.
Слайд 76Определение расстояния между двумя скрещивающимися прямыми
Г.Э.
Г.Э.
Задача решается в два действия.
Выбираем одну из прямых в качестве «главного элемента» и
располагаем
его параллельно плоскости проекций (например, к П2), чтобы прямая - Г.Э. проецировалась в натуральную величину. Вторая прямая является зависимой и преобразуется вместе с Г.Э.Слайд 77Определение расстояния между двумя скрещивающимися прямыми
Н.в.
Н.в.
2. Располагаем Г.Э.(СD) перпендикулярно
плоскости П1(С2'‘ D2 '‘= н.в. ┴ОХ).
На П1 прямая СD
проецируется в точку (С1≡D1). Вторая прямая строитсявслед за первой. ЕО - расстояние между двумя скрещивающимися прямыми.
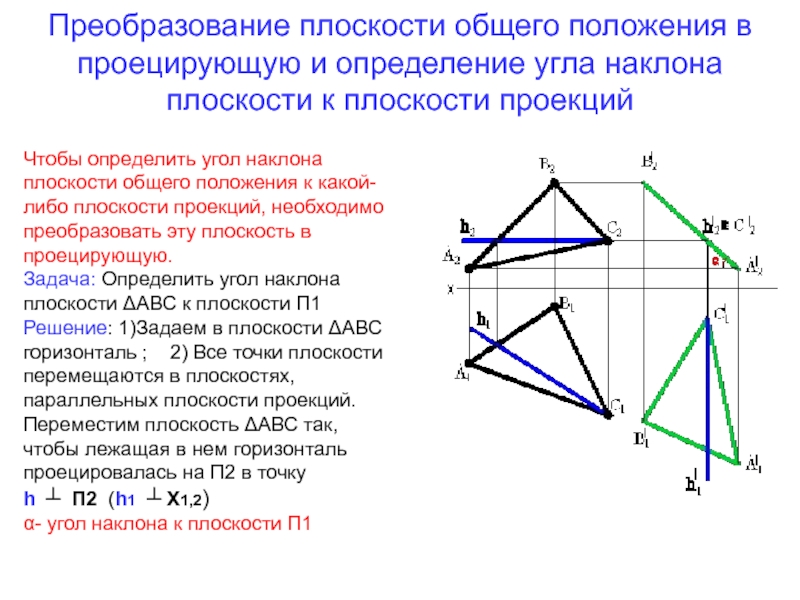
Слайд 78Преобразование плоскости общего положения в проецирующую и определение угла наклона
плоскости к плоскости проекций
Чтобы определить угол наклона плоскости общего положения
к какой-либо плоскости проекций, необходимо преобразовать эту плоскость в проецирующую.Задача: Определить угол наклона плоскости ΔАВС к плоскости П1
Решение: 1)Задаем в плоскости ΔАВС
горизонталь ; 2) Все точки плоскости перемещаются в плоскостях, параллельных плоскости проекций.
Переместим плоскость ΔАВС так, чтобы лежащая в нем горизонталь проецировалась на П2 в точку
h ┴ П2 (h1 ┴ Х1,2)
α- угол наклона к плоскости П1
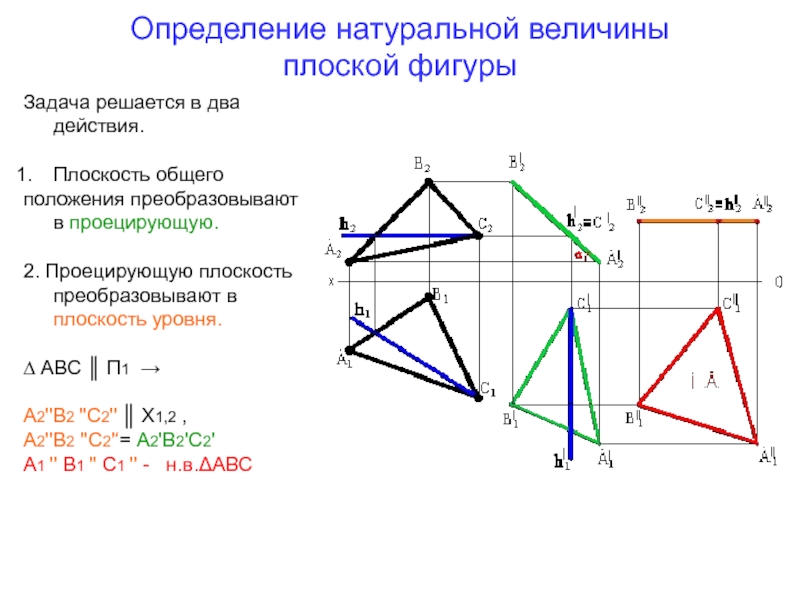
Слайд 79Определение натуральной величины
плоской фигуры
Задача решается в два действия.
Плоскость
общего
положения преобразовывают в проецирующую.
2. Проецирующую плоскость преобразовывают в плоскость
уровня.∆ АВС ║ П1 →
А2''В2 ''С2'' ║ Х1,2 ,
А2''В2 ''С2'‘= А2'В2'С2'
А1 '' В1 '' С1 '' - н.в.ΔАВС
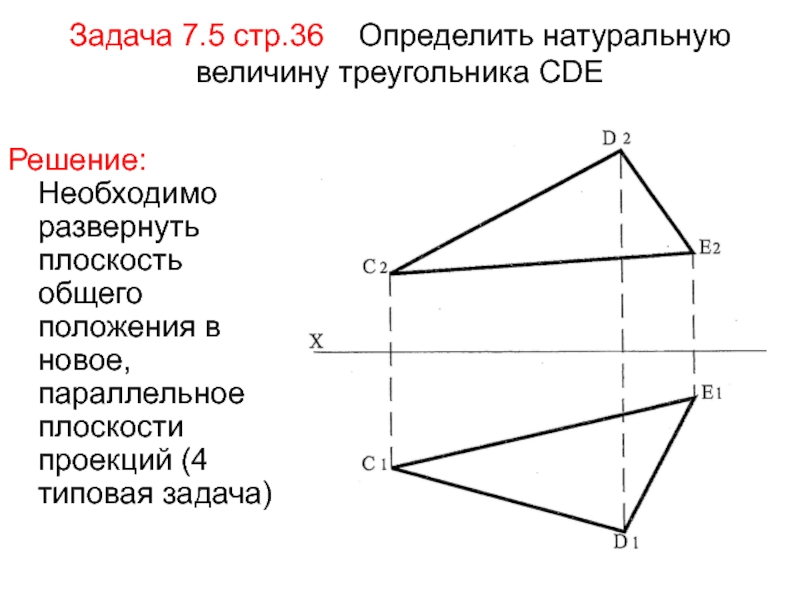
Слайд 80Задача 7.5 стр.36 Определить натуральную величину треугольника СDE
Решение: Необходимо
развернуть плоскость общего положения в новое, параллельное плоскости проекций (4
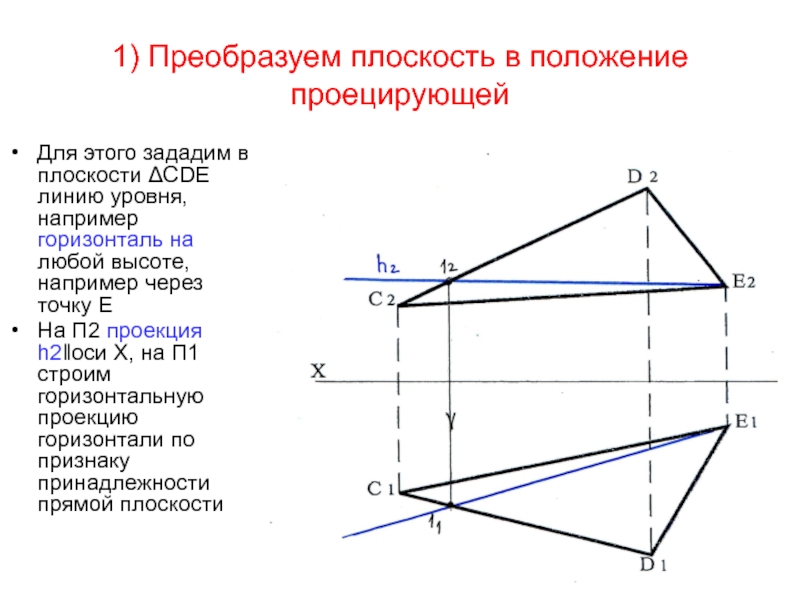
типовая задача)Слайд 811) Преобразуем плоскость в положение проецирующей
Для этого зададим в плоскости
ΔСDЕ линию уровня, например горизонталь на любой высоте, например через
точку ЕНа П2 проекция h2‖оси Х, на П1 строим горизонтальную проекцию горизонтали по признаку принадлежности прямой плоскости





![Лекция 5 Преобразование отрезка прямой общего положения в проецирующий (2 типовая задача)В том Преобразование отрезка прямой общего положения в проецирующий (2 типовая задача)В том случае, если [ АВ ] –](/img/thumbs/140a064f2bebdedf11eb330d589afc60-800x.jpg)

![Лекция 5 Отложим по траектории вращения точки В отрезок ВО1 = н.в.[ВО] и Отложим по траектории вращения точки В отрезок ВО1 = н.в.[ВО] и по траектории вращения точки С отрезок](/img/thumbs/1cd0e7efa007d64cf6538df659f16fcf-800x.jpg)

![Лекция 5 Преобразуем главный элемент- отрезок прямой ВС в положение проецирующего. На чертеже Преобразуем главный элемент- отрезок прямой ВС в положение проецирующего. На чертеже н.в. [ВС] = В2‘С2' располагаем перпендикулярно](/img/thumbs/07d264a9ce3f08ed30374d170e7e52e9-800x.jpg)
![Лекция 5 Находим недостающую проекцию АО на П2. Т.к. на П1 отрезок проецируется Находим недостающую проекцию АО на П2. Т.к. на П1 отрезок проецируется как н.в.[АО], на П2 его фронтальная](/img/tmb/3/293600/7fa9b0663b2f6a037c511eec46483c7b-800x.jpg)