Слайд 1Лекция 5
Дифракция Фраунгофера на многомерных структурах
5.1. Дифракция Фраунгофера на
плоских и пространственных решетках
5.2.Уравнения Лауэ. Спектроскопия рентгеновских лучей
5.3. Условия Брэгга-Вульфа
5.4. Дифракционные решетки с синусоидальной пропускаемостью
5.5. Оптическая фильтрация пространственных частот
5.6. Принципы голографии
Слайд 25.1. Дифракция Фраунгофера на плоских и пространственных решетках
В природе в
роли дифракционных решёток выступают вещества, имеющие кристаллическую структуру. Для таких
веществ характерно упорядоченное расположение атомов или молекул в пространстве. При их облучении электромагнитными волнами последние испытывают явление дифракции на атомах или молекулах, в результате становится возможными наблюдать перераспределение интенсивности падающей волны. Структура наблюдаемой дифракционной картины определяется закономерностями расположения атомов и молекул. По этой причине явление дифракции электромагнитных волн может быть использовано для исследования структуры строения вещества, а при известной структуре кристалла – для изучения спектрального состава излучения естественных и искусственных источников излучения.
При изучении свойств дифракционной решёток было установлено, что для увеличения их разрешающей способности и дисперсии расстояние между щелями d должно быть во много раз больше длины волны облучающей волны, т. е. d >> .
В кристаллах в роли щелей выступают атомы или молекулы, а период решётки определяется межатомным расстоянием d. Учитывая, что порядок величины d 10–8 м, для выполнения условия дифракции приходится пользоваться электромагнитные волны с очень малой длиной волны. Для этой цели подходят электромагнитные волны рентгеновского диапазона с длиной волны 10–12 м.

Слайд 3Изучение структуры кристаллических, а также поликристаллических веществ с помощью явления
дифракции электромагнитных волн рентгеновского диапазона составляет сущность рентгеноструктурного анализа.
Как известно,
структура расположения атомов в кристалле может иметь достаточно сложный, трёхмерный порядок, определяемый т.н. группами симметрии кристалла. Для упрощения рассуждений рассмотрим самый простой случай регулярного расположения атомов в кристаллических плоскостях вдоль прямых линий, параллельных оси OX, с межатомным расстоянием а, и рассмотрим их дифракционную картину.
Слайд 4Допустим, мы имеем почти монохроматический пучок рентгеновского излучения, направленный на
нашу линейную цепочку атомов. Условие усиления (усиливающей интерференции) выполняется, если
разность хода волн, рассеянных соседними атомами, кратные длины волны. Если пучок падает под углом 0 к линии атомов, разделенных интервалами a (период), то для угла дифракции разность хода, соответствующая усилению, запишется в виде a(cos – cos0) = h, где – длина волны, а h – целое число.
Слайд 55.2.Уравнения Лауэ. Спектроскопия рентгеновских лучей
Чтобы распространить этот подход на трехмерный
кристалл, необходимо лишь выбрать ряды атомов по двум другим направлениям
в кристалле и решить совместно полученные таким образом три уравнения для трех кристаллических осей с периодами a, b и c:
Пусть по отношению к осям выбранной декартовой системы координат a, b, c направление падения волны составляет углы, равные 0, 0, 0. Между этими углами существует связь, следующая из очевидного соотношения:
cos20 + cos20 + cos20 = 1.
a(cos – cos0) = h,
b(cos – cos0) = k,
c(cos – cos0) = l.
В результате дифракции рентгеновских волн будут наблюдаться дифракционные максимумы, угловое расположения которых имеет трёхмерный характер и задаётся для каждого из них углами , , , где h, k, l, = 1, 2, … – целые числа. Положение максимумов и межплоскостные расстояния связаны между собой, соотношениями, следующими из формулы Вульфа - Брэггов с учётом угла падения рентгеновской волны на кристалл.
Система уравнений используется для определения искомых значений межплоскостных расстояний h, k, l. Это – фундаментальные уравнения Лауэ для дифракции рентгеновского излучения.

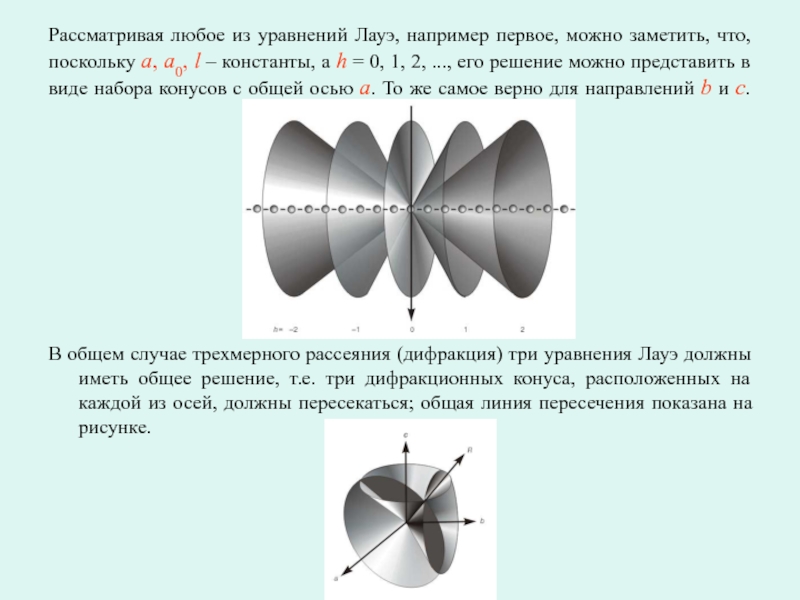
Слайд 6Рассматривая любое из уравнений Лауэ, например первое, можно заметить, что,
поскольку a, a0, l – константы, а h = 0,
1, 2, ..., его решение можно представить в виде набора конусов с общей осью a. То же самое верно для направлений b и c.
В общем случае трехмерного рассеяния (дифракция) три уравнения Лауэ должны иметь общее решение, т.е. три дифракционных конуса, расположенных на каждой из осей, должны пересекаться; общая линия пересечения показана на рисунке.
Слайд 7Совместное решение уравнений приводит к закону Брэгга – Вульфа:
= 2(d/n)sin, где d – расстояние между плоскостями с индексами
h, k и l (период), n = 1, 2, ... – целые числа (порядок дифракции), а q – угол, образуемый падающим пучком (а также и дифрагирующим) с плоскостью кристалла, в которой происходит дифракция.
Анализируя уравнение закона Брэгга – Вульфа для монокристалла, расположенного на пути монохроматического пучка рентгеновского излучения, можно заключить, что дифракцию непросто наблюдать, т.к. величины λ и фиксированы, а sin < 1. При таких условиях, чтобы имела место дифракция для рентгеновского излучения с длиной волны λ, плоскость кристалла с периодом d должна быть повернута на правильный угол . Для того чтобы реализовать это маловероятное событие, применяются различные методики.
Слайд 8Спектроскопия рентгеновских лучей
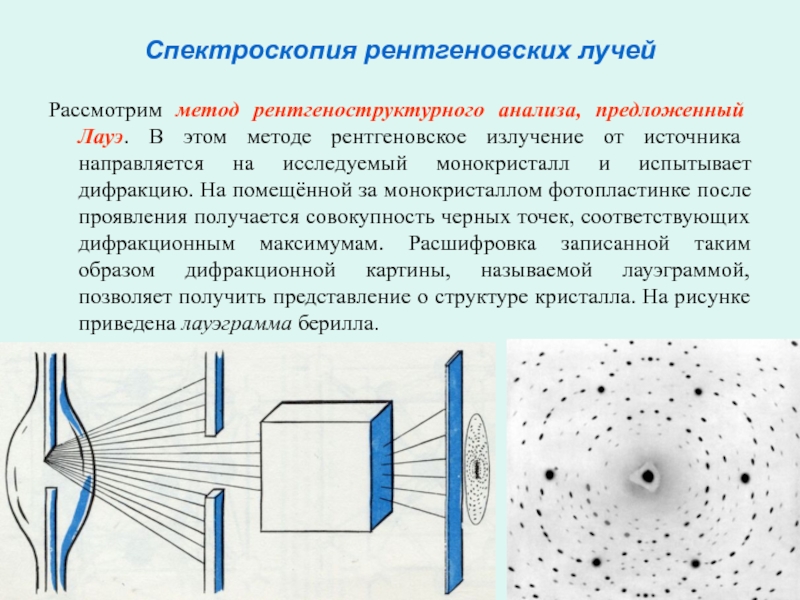
Рассмотрим метод рентгеноструктурного анализа, предложенный Лауэ. В
этом методе рентгеновское излучение от источника направляется на исследуемый монокристалл
и испытывает дифракцию. На помещённой за монокристаллом фотопластинке после проявления получается совокупность черных точек, соответствующих дифракционным максимумам. Расшифровка записанной таким образом дифракционной картины, называемой лауэграммой, позволяет получить представление о структуре кристалла. На рисунке приведена лауэграмма берилла.
Слайд 9Метод Лауэ применяется главным образом для исследования монокристаллов или крупнокристаллических
образцов. В этом методе неподвижный монокристалл освещается параллельным пучком лучей
со сплошным спектром.
Дифракционная картина, регистрируемая на фотопленку, расположенную перед кристаллом, называется эпиграммой. На лауэграммах дифракционные пятна располагаются по зональным кривым (эллипсам, параболам, гиперболам, прямым). Эти кривые являются сечениями дифракционных конусов плоскостью и касаются первичного пятна. На эпиграммах дифракционные пятна располагаются по гиперболам, не проходящим через первичный луч.
Для рассмотрения особенностей дифракционной картины в методе Лауэ пользуются геометрической интерпретацией с помощью обратной решетки. Лауэграммы и эпиграммы являются отображением обратной решетки кристалла. По лауэграмме можно получить представление о симметрии обратной решетки кристалла. По форме пятен лауэграммы судят о степени совершенства кристалла.
В методе Лауэ применяется непрерывный «белый» спектр рентгеновского излучения, которое направляется на неподвижный монокристалл. Для конкретного значения периода d из всего спектра автоматически выбирается соответствующее условию Брэгга – Вульфа значение длины волны.

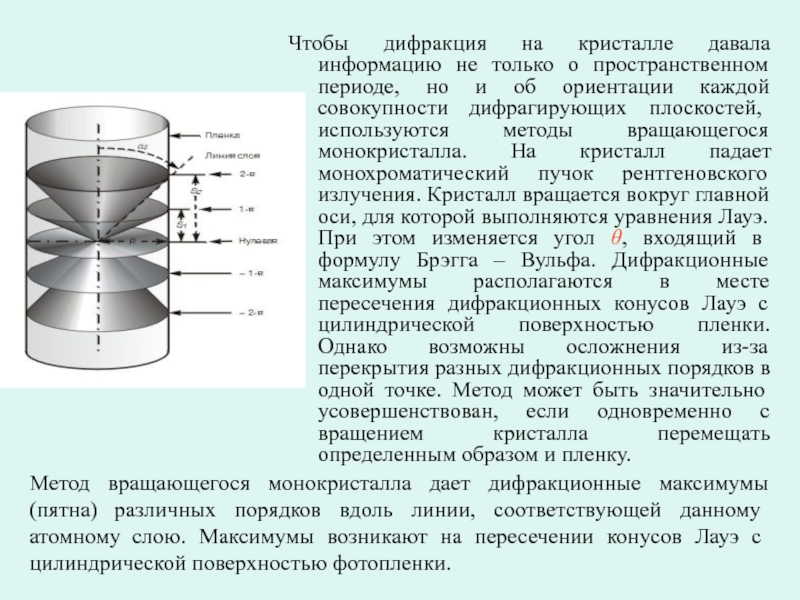
Слайд 10Чтобы дифракция на кристалле давала информацию не только о пространственном
периоде, но и об ориентации каждой совокупности дифрагирующих плоскостей, используются
методы вращающегося монокристалла. На кристалл падает монохроматический пучок рентгеновского излучения. Кристалл вращается вокруг главной оси, для которой выполняются уравнения Лауэ. При этом изменяется угол θ, входящий в формулу Брэгга – Вульфа. Дифракционные максимумы располагаются в месте пересечения дифракционных конусов Лауэ с цилиндрической поверхностью пленки. Однако возможны осложнения из-за перекрытия разных дифракционных порядков в одной точке. Метод может быть значительно усовершенствован, если одновременно с вращением кристалла перемещать определенным образом и пленку.
Метод вращающегося монокристалла дает дифракционные максимумы (пятна) различных порядков вдоль линии, соответствующей данному атомному слою. Максимумы возникают на пересечении конусов Лауэ с цилиндрической поверхностью фотопленки.
Слайд 11Другой метод рентгеноструктурного анализа был предложен Шерером и Дебаем для
исследования поликристаллических образцов. Поликристаллические образцы получаются в результате спекания измельчённого
в порошок кристаллического вещества. Изготовленный таким способом образец в форме проволочки O помещается на оси камеры, на боковые стенки которой помещается фотоплёнка P.
При облучении монохроматическим рентгеновским излучением от источника S поликристаллического образца O из-за беспорядочной ориентации кристаллических плоскостей различных его составляющих возникает конусы
направлений D1, D2, D3, … , в которых
для рассеянных волн выполнено
условие Вульфа - Брэггов.
На плёнке после проявления дифракционная
картина (дебаеграмма) будет иметь вид
колец или полос. Анализ дебаеграммы
позволяет определить основные элементы
структуры кристалла.
Слайд 125.3. Условия Брэгга-Вульфа
Условие Брэгга - Вульфа, определяет положение интерференционных максимумов
рентгеновских лучей, рассеянных кристаллом без изменения длины волны. Оно было
установлено в 1913 независимо друг от друга английским учёным У.Л. Брэггом и русским учёным Г.В. Вульфом вскоре после открытия немецким учёным М. Лауэ и его сотрудниками дифракции рентгеновских лучей. Толкование рентгеновской дифракционной картины, полученной в опыте Лауэ, оказалось довольно сложным. Брэгг и Вульф решили эту задачу рассмотрев рассеяние рентгеновских лучей как отражение от атомных плоскостей, которые условно можно провести через центры атомов, образующих кристалл. Атомы при этом считались неподвижными, и кристалл представлялся в виде семейства параллельных плоскостей, находящихся на одинаковом расстоянии друг от друга. Предполагалось, что число атомных плоскостей велико, а преломления нет.
Слайд 13Пусть на кристалл под некоторым углом скольжения к плоскостям
с межплоскостным расстоянием d падает параллельный пучок монохроматических ( =
const) лучей. Отраженные от различных плоскостей (p-p' и q-q') одного и того же семейства лучи интерферируют, ослабляя или усиливая друг друга в зависимости от разности хода Δ:
Δ = BC - AC = [1-cos(2)]d/sin() = 2dsin().
Интерференционный максимум будет наблюдаться, когда выполняется условие
2dsin = m,
где d - межплоскостное расстояние, – угол скольжения, т. е. угол между отражающей плоскостью и падающим лучом, - длина волны рентгеновского излучения и m – так называемый, порядок отражения, т. е. положительное целое число, известное как формула Брэгга - Вульфа и связывающее угол скольжения , при котором происходит отражение рентгеновских лучей кристаллом (брэгговский угол), с межплоскостным расстоянием d в кристалле и длиной волны падающих лучей .
Слайд 14Условие Брэгга - Вульфа выполняется при рассеянии кристаллами не только
рентгеновских лучей, но также при дифракции электронов, протонов и нейтронов.
Нужно
подчеркнуть, что кристалл отражает рентгеновские лучи только при определенных углах скольжения , удовлетворяющих условию максимумов и названных брэгговскими углами, то есть в отличие от зеркал оптики видимого света кристалл отражает рентгеновские лучи селективно.
Другое важное отличие обусловлено тем, что расходимость падающего на кристалл пучка рентгеновских лучей значительно превышает угловой интервал, в котором происходит отражение, и в результате отражается лишь очень небольшая часть падающей энергии. Зеркало же отражает все лучи светового пучка, благодаря чему отражается и значительная часть световой энергии.
Уравнение Брэгга - Вульфа является основой рентгеновского анализа. Оно указывает, как можно, зная длину волны падающего излучения и измеряя брэгговские углы, найти межплоскостные расстояния в кристалле. В свою очередь, для каждого семейства параллельных плоскостей совокупность направлений селективного отражения связана с межплоскостными расстояниями соотношениями, позволяющими рассчитать размеры и форму элементарной ячейки кристалла и, следовательно, изучать строение кристаллической решетки.

Слайд 155.4. Дифракционные решетки с синусоидальной пропускаемостью
Обычно у дифракционной решетки коэффициент
пропускания τ амплитуды равен 1 на щелях и 0 на
непрозрачных частях. Тогда амплитуда падающей на решетку волны А0, то амплитуда выходящей из решетки, волны равна А = А0τ = А0 (на щелях), и A = 0 (на непрозрачных частях).
Для описания прохождения света через дифракционную решетку можно применить метода Фурье, который в этих задачах сводится к представлению произвольных функций в виде дискретной или непрерывной совокупности гармонических функций. Для нас основной интерес представляет не временной ход процессов, а пространственная структура поля, заданная в некоторой плоскости в виде функции координат f(х,у), или в простейшем (одномерном) случае – в виде функции одной координаты f(x), которая есть комплексная амплитуда поля волны света.
Фурье-разложение функции f(x) позволяет представить волновое поле в виде совокупности плоских волн, что упрощает решение многих задач распространения и дифракции волн.
Слайд 16В курсах математики доказывается, что любую периодическую функцию f(x) периода
можно представить в виде дискретного ряда Фурье
где kn =
nk0 = 2πn/ – волновой вектор n-ой гармонической составляющей, Cn – комплексная амплитуда n-ой гармоники
Совокупность коэффициентов Cn называют спектром функции f(x). Дискретный спектр периодической функции f(t) можно изобразить графически, откладывая по оси ординат амплитуды гармоник Cn.
Легко показать, что если функция f(x) – действительная, то C–n = C*n (знак * означает комплексную сопряженность). Тогда C–nexp[–ink0x] + Cnexp[ink0x] = 2Cncos(nk0x + n), где n = argCn. (Использовано соотношение Эйлера cos = ½(exp(i) + exp(–i).)
Следовательно, ряд Фурье можно записать в виде
где a0 = C0, an = 2Cn.
Слайд 17Рассмотрим в качестве примера периодическую последовательность прямоугольных штрихов шириной
и периодом . Тогда
Здесь k0 = 2π/, A –
амплитуда штрихов.
Это есть описание с помощью Фурье-преобразования дифракции света на бесконечной амплитудной дифракционной решетке с прямоугольной функцией прозрачности.
В ряде случаев спектр функции может быть найден с помощью простейших тригонометрических преобразований без вычисления интеграла. Примером может служить амплитудно-модулированное колебание вида f(x) = A[1 + mcos(2πx/d)]cos0x, где функция a(x) = A[1 + mcos(2πx/d)] выражает гармонический закон амплитудной модуляции. Легко видеть, что
f(x) = Acos(2πx/0) + (Am/2)cos(2πx/0 + 2πx/d) +
+(Am/2)cos(2πx/0 – 2πx/d).
Следовательно, дифракционная картина состоит из трех линий: линии распространяющаяся под углом φ = 0, которая соответствует просто прямолинейному распространению волны через однородную среду, и двух линий, дифрагированных под углами φ(+) и φ(–), определяемых из условий 2π/d – ksinφ(+) = 0, 2π/d + ksinφ(–) = 0. Учитывая, что k = 2π/, можно эти условия записать в виде dsinφ(+) = , dsinφ(–) = –.

Слайд 18Теперь ясно, как можно рассмотреть дифракцию на произвольной периодической структуре.
Надо, представить ее характеристики рядом Фурье, рассмотреть дифракцию, описываемую отдельными
членами ряда Фурье. Совокупность этих дифракций составляет всю дифракционную картину на периодической структуре. Дифракцию на непериодической структуре можно рассмотреть аналогично. Но только в этом случае надо вместо ряда Фурье использовать интеграл Фурье
Периодическую функцию, выражающую коэффициент пропускания решетки с периодом d, можно разложить в ряд Фурье по гармоническим функциям, периоды которых равны d, d/2, d/3, .... Дифракция волны длиной волны , падающей на решетку, сводится к дифракции на гармонических структурах, составляющих решетку, которые были получены разложением коэффициента пропускания решетки в ряд Фурье. При дифракции на гармонической составляющей структуры с длиной d/m возникают два дифракционных максимума, условия для которых имеют вид (d/m)sinφm = m, (d/m)sinφ-m = -m или
dsinφ = m (m = ±1, ±2, ...).
Слайд 195.5. Оптическая фильтрация пространственных частот
Пространственная фильтрация изображений основывается на возможности
изменить изображение, воздействуя определенным образом на дифракционную картину предмета в
фокальной плоскости линзы.
Сущность пространственной фильтрации изображений. Дифракционное образование изображения сводится к двум стадиям:
1) формированию в фокальной плоскости линзы дифракционной картины предмета;
2) преобразованию дифракционной картины предмета в фокальной плоскости линзы в изображение предмета в плоскости изображений.
Вся информация, имеющаяся в изображении предмета, содержится также и в дифракционной картине предмета в фокальной плоскости. Если произвести в фокальной плоскости изменения дифракционной картины, например, закрыть или, наоборот, усилить некоторые максимумы, то произойдет соответствующее изменение в изображении предмета. Внесение изменений в изображение предмета посредством модификации дифракционной картины предмета, из которой в последующем, формируется изображение, называется пространственной фильтрацией изображения.
Слайд 20Пространственная фильтрация изображений дифракционной решетки.
Наиболее наглядно существо пространственной фильтрации
можно проиллюстрировать на примере изображения дифракционной решетки.
Дифракционная решетка, расстояние s1
которой до линзы больше фокусного, освещается параллельным пучком лучей. Линза L создает в плоскости Р, расстояние s2 которой от линзы, действительное перевернутое изображение решетки, состоящее из темных и светлых полос с достаточно резкими границами. В фокальной плоскости F линзы создается картина дифракции Фраунгофера на решетке. Если ее наблюдать на реальной плоской поверхности, то она представляется в виде дифракционных полос. Если эта поверхность воображаемая и лучи беспрепятственно проходят дальше, то в плоскости Р образуется изображение решетки.
Слайд 21Наиболее полное изображение решетки получается тогда, когда вся дифракционная картина
в плоскости Р0 участвует в образовании изображения в плоскости Р2.
Если часть максимумов задержать, то изображение ухудшится, пропадут некоторые детали или даже полностью исказится изображение решетки.
Например, устраним все максимумы, за исключением главного. Это соответствует лучу, прошедшему при отсутствии препятствий на его пути. В плоскости Р наблюдается равномерное освещение, изображение дифракционной решетки отсутствует, ее как бы не существует. Устраним все нечетные максимумы. Оставшиеся максимумы соответствуют картине дифракции на решетке, период которой вдвое меньше. Поэтому в плоскости изображений возникает изображение дифракционной решетки с вдвое меньшим периодом, т. е. более частая решетка. Максимумы первых порядков определяют более крупные детали объекта, а информация о более мелких деталях передается через максимумы более высоких порядков.
Изменение изображения посредством воздействия не на само изображение, а на распределение амплитуд, из которых в последующем синтезируется изображение, составляет суть пространственной фильтрации. Основная задача при этом состоит в создании фильтра, который нужным образом изменяет проходящую через него волну.

Слайд 22В общем случае можно сказать, что при прохождении светового пучка
через линзу осуществляется (с точностью до фазовых множителей) двумерное разложение
Фурье предметного поля в спектр по пространственным частотам. Этот спектр выглядит как множество дифракционных максимумов и минимумов интенсивности в фокальной плоскости линзы. При дальнейшем распространении световых волн из фокальной плоскости происходит их перекрывание и интерференция, в результате чего осуществляется обратный спектральному разложению процесс – синтез пространственных гармоник предметного поля, приводящий к формированию изображения. Преимущество такой волновой картины формирования изображения в том, что она открывает скрытые от геометрической оптики возможности преобразования изображений. Если в задней фокальной плоскости помещать различные маски – экраны с разного сорта отверстиями, то с точки зрения геометрической оптики просто пропускаются не все лучи от каждой из точек предмета. С этой точки зрения должна уменьшаться интенсивность изображения, но структура его не должна меняться. В действительности же введение масок может существенно изменить изображение. С волновой точки зрения масками изымается часть пространственных частот предметного поля на пути светового пучка через фокальную плоскость в плоскость изображения. В итоге в формировании изображения участвуют только оставшиеся после фильтрации частоты, и изображение уже не оказывается точной оптической копией предмета. Этим методом, открытие которого принадлежит Аббе, можно изменять качество изображений в желаемую сторону. Например, если изображение засорено не представляющими интерес мелкими деталями, можно с помощью экрана с отверстием, расположенным в центре фокальной плоскости, отрезать высокие пространственные частоты и тем самым очистить изображение от нежелательной «грязи». Напротив, перекрыв или притушив низкие частоты в близких к центру точках фокальной плоскости, можно подчеркнуть в изображении мелкие детали и тем самым «оконтурить» крупные фрагменты изображения.

Слайд 23Эксперимент Аббе — Портера
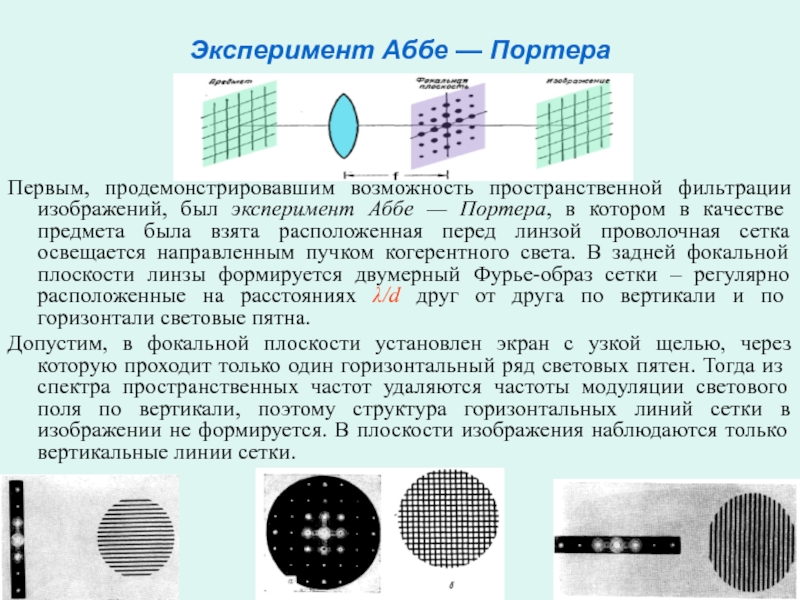
Первым, продемонстрировавшим возможность пространственной фильтрации изображений,
был эксперимент Аббе — Портера, в котором в качестве предмета
была взята расположенная перед линзой проволочная сетка освещается направленным пучком когерентного света. В задней фокальной плоскости линзы формируется двумерный Фурье-образ сетки – регулярно расположенные на расстояниях λ/d друг от друга по вертикали и по горизонтали световые пятна.
Допустим, в фокальной плоскости установлен экран с узкой щелью, через которую проходит только один горизонтальный ряд световых пятен. Тогда из спектра пространственных частот удаляются частоты модуляции светового поля по вертикали, поэтому структура горизонтальных линий сетки в изображении не формируется. В плоскости изображения наблюдаются только вертикальные линии сетки.
Слайд 24Очевидно, что поворотом щели в вертикальное положение можно устранить в
изображении сетки вертикальные линии, оставив горизонтальные. Перекрывая горизонтальные ряды пятен
интенсивности через один ряд, можно получить удвоение горизонтальных линий в изображении, то есть ложные элементы в изображении. Перекрывание центрального максимума интенсивности приводит к обращению контраста – негативному изображению.
Если непрозрачной пластиной с щелью закрыть в фокальной плоскости все максимумы интенсивности, за исключением центрального и находящихся с ним на одной линии, параллельной одной из систем штрихов решетки, то в изображении сохраняется лишь перпендикулярная система штрихов решетки. Если закрыть центральный максимум, то получается изображение решетки с обращенным контрастом — на месте светлых линий возникают темные, и наоборот.
Слайд 25Рассмотрим процесс оптической фильтрации при когерентном освещении. На рисунке показана
классическая схема оптической фильтрации. Пусть объектом служит, фотопластинка с изображением
пейзажа. Объект освещен параллельным пучком монохроматического света. Если он находится от линзы Л2 на расстоянии f, равном её фокусному расстоянию, то преобразование Фурье объекта лежит в задней фокальной плоскости линзы Л2. Это преобразование Фурье есть не что иное, как картина дифракции на объекте. Поместим в фокальной плоскости линзы Л2 фильтр, который изменит распределение комплексных амплитуд в этой плоскости. Таким фильтром может быть маленький непрозрачный экран, который задерживает часть дифрагированного света в непосредственной близости от оптической оси линзы, соответствующую крупным деталям объекта (т.е. низким пространственным частотам). Экран не мешает распространению лучей, дифрагированных мелкими деталями объекта (высокие пространственные частоты) и распространяется дальше от оси. Если третья линза Л3 образует в плоскости А1 изображение объекта А, то крупные детали не будут воспроизведены на его изображении. Зато мелкие детали будут относительно усилены и видны лучше, что создаст впечатление увеличения четкости фотографии. Здесь приведен только один пример, но оптическая фильтрация более эффективна, если использовать разные фильтры. В некоторых областях, например при распознавании образов используются фильтры, которые регистрируют одновременно и фазу, и амплитуду. Эти фильтры представляют собой голограммы.

Слайд 26Теория и эксперимент показывают, что сходство объекта и его оптического
изображения будет тем лучше, чем полнее используется пространственный спектр объекта.
С другой стороны, если отдельные пространственные частоты исключить из процесса формирования изображения, то могут возникнуть существенные искажения изображения. Процесс изменения изображения объекта, подчеркивание его отдельных структурных особенностей путем выделения тех или иных пространственных частот носит название оптической пространственной фильтрации.
Аппарат Фурье-преобразований позволяет делать не только анализ, но и синтез оптических систем. А именно это требуется при конструировании приборов.
Другим методом фильтрации полезного сигнала на фоне шумов является метод Цернике, который он применил для наблюдения прозрачных объектов.
Нидерландский физик Фриц Цернике (1888-1966) заинтересовался щелевым эффектом в дифракционных решетках. Многие ученые замечали, что решетки, содержащие повторяющиеся ошибки в расположении бороздок, вызванные неполадками в механизме, наносившем эти бороздки, порождают лишние линии, названные призраками, с каждой стороны выделяющейся яркой линии. Они считали эти линии не заслуживающими внимания и давали их появлению разные объяснения. Цернике предложил свое объяснение. Полагая, что призраки возникают из-за фазовых сдвигов, вызванных погрешностями изготовления решеток, он выполнил серию экспериментов, которые не только подтвердили его правоту, но и привели его к изобретению прибора, названного им фазово-контрастным микроскопом.

Слайд 27При работе с относительно прозрачными препаратами, как это бывает в
медицине и биологии, обычные микроскопы обладают рядом серьезных дефектов. Цернике
полагал, что свет, проходящий сквозь прозрачные детали в препаратах, отличается от света, который проходит мимо них, и, следовательно, содержит нужную информацию. Разница здесь не в амплитуде, которую может обнаружить глаз, а в фазе, которую глаз отличить не в состоянии. Фазы же отличаются, поскольку свет движется с разными скоростями в различных веществах. Если вещество прозрачно, то оно не меняет количество пропускаемого света, но изменяет число длин волн или долей длин волн, укладывающихся по всей длине оптического пути, ибо оно понижает скорость света и, следовательно, расстояние, проходимое за один период колебания. Обычно говорят, что оно приводит к запаздыванию фазы. Цернике в своих экспериментах с призраками дифракционных решеток нашел способ превращения фазовых изменений в амплитудные, которые и позволяли сделать прозрачные детали видимыми для глаза.
Принцип состоял в том, чтобы наложить свет, проходящий сквозь прозрачный объект, на однородное фоновое освещение, представляющее собой небольшую порцию прямого света (света, обтекающего объект), который намеренно обладает опережением по фазе на четверть длины волны. В результате сочетания света, проходящего сквозь прозрачный объект, который обладает запаздыванием по фазе относительно прямого света, с фоновым освещением, которое имеет опережение по фазе, образуется деструктивная интерференция, т.е. понижение яркости. Для глаза наблюдателя это выглядит так, как если бы объект поглощал свет. Цернике добивался нужного фонового освещения, помещая то, что он называл фазовой пластиной (стеклянная пластина с выгравированной бороздкой), на пути луча света в фокальной плоскости линз объектива у микроскопа.

Слайд 28В микроскопе Цернике лучи света проходят через апертурную диафрагму, отверстие
которой имело форму кольца, а вблизи заднего фокуса объектива помещается
так называемая фазовая пластинка, имеющая кольцевидный выступ, или канавку. Лучи света, которые свободно проходил через объект, проходил и через фазовое кольцо, в то время как лучи, рассеянные объектом, отклоняются в сторону. В связи с тем, что толщина пластинки различна, возникала разность фаз волн двух световых потоков. В конечном счете, в окуляре происходит интерференция лучей, что значительно повышает контрастность изображения. Иными словами, в пластинке различие в фазе волны преобразуется в различие амплитуд, т. е. яркости.
Фазово-контрастный микроскоп Цернике сделал возможным наблюдение бесцветных организмов, таких, как клетки или бактерии, без применения красителей, которые зачастую убивали образцы. Он позволял проводить более точные наблюдения, чем те, которые можно было получить с освещением темного поля, - еще один метод, часто приводивший к неправильной интерпретации мелких деталей. Фазово-контрастный метод оказался также полезным при оценке неровностей оптических поверхностей, например зеркала телескопа, да и самих дифракционных решеток, давших рождение самой этой идее.
В 1953 году Цернике был награжден Нобелевской премией по физике «за обоснование фазово-контрастного метода, особенно за изобретение фазово-контрастного микроскопа».

Слайд 305.6. Принципы голографии
Для записи и воспроизведения информации не только об
амплитудах, но и о фазах волновых фронтов, используется способ, получивший
название - голография. В переводе с греческого языка это слово означает «полная запись».
Идея лежащая в основе голографии аналогична методу синхронного детектирования, известному в радиотехнике. Информация передается в виде модулированного сигнала на высокой несущей частоте: Vm = V0m[1 +mf(t)]cost, где — несущая частота, f(t) — передаваемый сигнал, m — глубина модуляции.
В модулированном сигнале содержится информация не только об амплитудном, но и о фазовом спектре функции f(t). Эту информацию можно выделить с помощью синхронного детектирования.
В радиотехнике известны устройства, которые позволяют перемножать напряжения подаваемых на них сигналов и получать на выходе их произведения. Если в такое устройство подать модулированный сигнал и сигнал несущей частоты Vн = Vонcost, то на выходе получим сигнал Vвых = αV0mVн = αV0mV0н[1 +mf(t)](l + cos2t)/2, где α — некоторая постоянная. Высокочастотная составляющая с помощью соответствующего фильтра устраняется, а оставшийся низкочастотный сигнал V(н)вых = A[l+mf(t)] содержит полную информацию об амплитудном и фазовом спектрах модулированного сигнала.

Слайд 31Логично использовать подобный синхронному детектированию прием и в световом диапазоне
частот. Для этого необходимо информацию, содержащуюся в световой волне, записать
в виде модулированной волны наложенной на некоторую несущую частоту. При записи модулированной волны на фотопластинку информация о фазе записываемой волны сохраняется. По записи на фотопластинке модулированной волны синхронным детектированием, т. е. ее облучением несущей частотой, можно восстановить исходную волну. Задача о полном восстановлении волнового фронта тем самым принципиально будет решена.
Для того чтобы осуществить этот метод в световом диапазоне, необходимо иметь излучение с достаточно высокой степенью когерентности. Такое излучение получается с помощью лазеров.
Фотопластинка, на которой записана информация о модулированной световой волне, называется голограммой. Задача голографии состоит в разработке методов записи голограмм и восстановлении по ним волнового фронта.
Слайд 32Голограмма плоской волны
Волна с несущей частотой называется опорной, а
волна, содержащая информацию об объекте, — сигнальной.
Плоская сигнальная волна
частотой распространяется в положительном направлении оси Z, перпендикулярно которой в плоскости XY расположена фотопластинка. Опорная волна образуется делением волнового фронта и с помощью призмы направляется на фотопластинку, перекрываясь на ней с сигнальной волной, также возникающей при делении волнового фронта Угол наклона опорной волны с осью Z обозначен .
Сигнальная и опорная волны записываются в виде Ес = E1exp[–i(t – kz)], Еоп = E0exp[–i(t – kzz – kxx)].
Учитывая, что kx = ksin, kz = kcos k с точностью до величин второго порядка по углу , который предполагается малым, можем Еоп представить в виде Eоп = E0exp[–i(t – kz – kxsin)].
Полная амплитуда напряженности электрического поля в плоскости фотопластинки равна Е = Ес + Еоп = еxp{–i(t – kz[E1 + E0exp(ikxsin)]}, где Е1 и Е0 можно считать действительными амплитудами. Отсюда для распределения интенсивностей находим выражение I(х) = E2/2 = [E21 + E20 + 2E0E1cos(kxsin)]/2, которое свидетельствует о том, что на фотопластинке в этом случае также записана и разность фаз между опорной и сигнальной волнами, т. е. фаза сигнальной волны, если считать фазу, опорной волны заданной.

Слайд 33Волновой фронт произвольного объекта складывается из волновых фронтов, порождаемых его
точками. Поэтому запись голограммы произвольного объекта осуществляется аналогично предыдущему случаю,
необходимо лишь, чтобы сигнальная несущая информацию об объекте волна была когерентна с опорной. Для этого надо объект освещать волной когерентной с опорной. Это можно сделать различными способами.
Голографическое изображение в отличие от фотографического имеет трёхмерный характер, т.е. его можно рассматривать под различными углами. Распределение интенсивности на поверхности фотопластинки имеет вид системы чередующихся максимумов и минимумов.
По существу голограмма представляет собой интерферограмму опорной и предметной волн, распределение интенсивности на поверхности которой определяется их разностью фаз.
Для голограмм, записываемых на фотопластинке с «толстым» слоем фотоэмульсии, при записи голограммы образуется объёмная структура зерён серебра, в виде «отражающих слоёв» и соответствующая распределению максимумов интенсивности, освещающей голограмму волны, которая передаёт кривизну записываемых волновых фронтов. В результате при восстановлении мнимого изображения предмета с таких голограмм не возникает его действительного двойника.
В объёмных голограммах пространственную структуру отражающих слоёв внутри голограммы можно рассматривать как объёмную дифракционную решётку, в которой направление на дифракционный максимум связано с межплоскостным расстоянием и длиной волны условием Вульфа - Брэггов. Тогда, для определения углового направления, в котором наблюдается восстанавливаемое с голограммы изображение, может быть определено с помощью формулы Вульфа - Брэггов.
По способу записи голограммы различаются на амплитудные и фазовые, в которых при восстановлении записанного на них изображения изменяется фаза проходящего светового потока пропорционально распределению интенсивности на поверхности интерферограммы волновых фронтов.

Слайд 34Основные параметры голограмм
Голограммы имеют сходство с дифракционной решётки. Следуя
этой аналогии, можно ввести понятие разрешающей способности голограммы. Чем больше
ее разрешающая способность, тем более чёткое (контрастное) изображение объекта может быть получено при его восстановлении. Как для дифракционной решётки с увеличением числа штрихов и размера увеличивается её разрешающая способность, так и для голограммы с увеличением площади голограммы происходит увеличение чёткости изображения получаемого с голограммы. Всем известное суждение о возможности получения изображения с любой части голограммы записанного на нём изображения объекта, не следует понимать буквально. Дело в том, что изображение, полученное с малых частей голограммы, может быть нечётким из-за малой разрешающей способности голограммы, используемой для восстановления изображения записанного на нёй объекта.
Слайд 35Другим важным параметром голограммы является её дифракционная эффективность. Она определяется
как отношение мощности светового потока, формирующего изображение объекта, записанного на
голограмме, к мощности потока опорной световой волны. Как видим, дифракционная эффективность голограмм представляет собой параметр, который сродни коэффициенту полезного действия, широко используемому в физике и технике. Различные виды голограмм обладают различной дифракционной эффективностью.
Как показывают расчёты, для тонких амплитудных голограмм их дифракционная эффективность не может превышать 6,5% . Для объёмных голограмм дифракционная эффективность не может превышать 13%.
Для повышения эффективности голограмм используются т.н. фазовые голограммы.
Теоретическим пределом эффективности тонких фазовых голограмм является величина, равная 33.5.%. Использование специальных схем записи фазовых голограмм позволяет увеличить их эффективность до 96%.
Различие между фазовой и амплитудной голограммой можно показать на примере зонной пластинкой Френеля (которая, на самом деле, является голограммой). Фазовая пластинка по сравнению с амплитудной пропускает в два раза больше света. Это объясняется тем, что в амплитудной пластине часть падающего на нее света задерживается закрытыми участками её апертуры. По этой причине понятно стремление использовать для получения качественных изображений объектов фазовую голографию, поскольку при этом уменьшаются потери энергии источника света, идущие на формирование изображения записанного на голограмме.

Слайд 36Применение голографии
Голографическая интерферометрия. Одно из самых главных преимуществ голографической
интерферометрии перед оптической это возможность записи голограмм состояний объекта, меняющегося
во времени, и последующий анализ изменений этих состояний после того, как эволюция объекта завершилась и даже сам объект может быть уже прекратил своё существование. Возможность записи на голограмме различных состояний объекта была предложена Д. Габором. Его идея заключалась в том, что в результате многократной экспозиции на голограмме записывается несколько изображений объекта, которые после освещения опорной волной могут интерферировать, поскольку являются взаимно когерентными. Это позволяет сравнить интерференционные картины, соответствующие разным состояниям объекта.
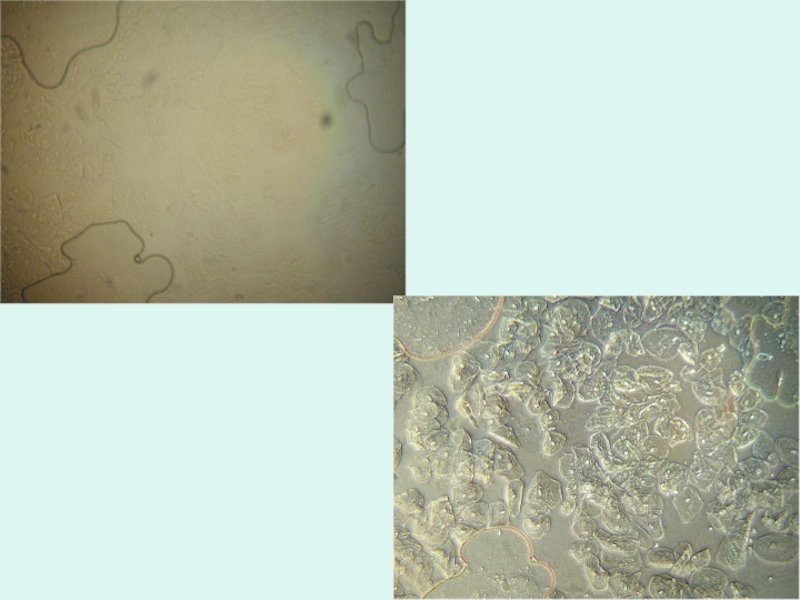
Слайд 37На рисунке приведена фотография интерферограммы ударной волны движущейся пули, получающейся
при восстановлении изображения с голограммы, записанной двумя короткими лазерными импульсами.
С помощью первого импульса записывалась голограмма «фона» - среды до пролёта пули, а вторым импульсом записывалось изображение пули в полёте. В результате пролёта пули возникают пространственно распределённые изменения плотности среды, а, следовательно, и соответствующего им изменение показателя преломления.
Объёмное изображение высокого качества. Традиционное применение объемного голографического изображения высокого качества относится к сфере культуры, образования для создания макетов оригиналов памятников культуры и искусства. Другая сфера применения объемного голографического изображения высокого качества тренажёры для обучения пилотирования самолётов, космических кораблей и овладения навыками работы в сложных условиях.
Голографические оптические элементы. Голограмма может быть использована не только в качестве носителя в закодированном виде изображения исследуемого объекта, но и как оптическое устройство, формирующее изображение. Например, можно использовать голограмму в качестве линзы, дифракционной решётки, светоделителей и других устройств преобразования светового потока.
Голограммы можно синтезировать с помощью ЭВМ. Особенностью таких голограмм является возможность создания на их основе устройств голографического преобразования волновых фронтов, которые другим способом сделать затруднительно или вовсе невозможно..

Слайд 38Другим достаточно широко используемым на практике голографическим оптическим устройством является
голографическая дифракционная решётка. Использование голограммы в качестве дифракционной решётки очевидно,
поскольку как отмечалось выше, голограмма по существу является дифракционной решёткой. Голографические решётки гораздо более просты в изготовлении обычных, дешевле их и не имеют дефектов, связанных с технологией нарезания щелей.
Голографические оптические элементы находят применение в качестве элементов, корректирующих искажение изображений объектов в оптических системах. Искажения в оптических системах могут возникать вследствие разнообразных причин, связанных как с технологией изготовления системы, в результате которой неизбежно имеет место некоторый разброс параметров характеристик элементов, отличающих их от заданных, так и эксплуатацией системы из-за влияние температурных деформаций, климатических факторов, неблагоприятных внешних воздействий случайного и искусственного происхождения.
Метод компенсации искажений с помощью голографических корректирующих элементов по существу основан на идее обращения направления распространения волнового фронта от источника изображения, в результате которого мнимое изображение объекта превращается в действительное. Этот подход может быть использован для компенсации искажений изображений предметов при их рассмотрении через искажающую среду.

Слайд 39Искажённое восприятие изображения объекта, волновой фронт от которого прошёл искажающую
среду, в основном связан с «порчей» фазы распространяющейся волны в
среде. В качестве корректирующего искажение изображения объекта может быть использована голограмма волнового фронта от объекта и плоской волны опорного источника (рис. a), получаемая в плоскости наблюдения изображения. При условии, что волны от опорного источника и объекта проходят искажающую среду и одинаковым образом искажаются средой, параметры которой не меняются за время прохождения волны.
Если осветить голограмму волной опорного источника (рис. b), то в соответствии со свойствами голограммы возникнет неискажённые средой действительное и мнимое изображение объекта.
Слайд 40Голографическая обработка информации
С помощью голографии можно решить достаточно обширный
класс задач обработки информации. Одним из примеров плодотворности голографического подхода
был приведен выше при рассмотрении изображения объекта, искажённого средой.
При обработке оптических изображений основной задачей является фильтрация светового потока, переносящего изображения объектов, с помощью фильтра с заданной пространственной частотной характеристикой. Важный частный случай этой задачи представляет согласованная фильтрация оптических сигналов, которая возникает при максимизации отношения мощностей обрабатываемого полезного изображения к мощности шумов, а также используется для распознавания обрабатываемых изображений.
Задача распознавания изображений объектов состоит в классификации исследуемого изображения, т.е. отнесения его к той или группе объектов, имеющих общие черты. Такие задачи появляются при автоматическом распознавании цифр на почтовом индексе, всевозможных штрих кодов, шифров доступа, отпечатков пальцев и т.п.
Задача согласованной фильтрации оптических сигналов состоит в построении оптического фильтра, обладающего заданной пространственной частотной характеристикой, определяемой комплексно сопряжённым пространственным спектром полезного изображения или классифицируемого объекта. Метод решения этой задачи с помощью голографии был предложен Ван дер Люгтом в 1963 году.

Слайд 41Системы голографической памяти
В системах оптической памяти используется побитовое представление
информации, когда нулю соответствует малый непрозрачный элемент изображения (пиксель), а
единице - прозрачный. Сразу с освоением лазеров начали разрабатываться поточечные системы оптической памяти на светочувствительной среде. При освещении светом в такой среде увеличивается оптическая плотность в том месте, куда падает записывающий световой пучок, и данная часть среды перестаёт пропускать свет. Считывание информации производится световым лучом, последовательно проходящим светочувствительную пластинку от одного пикселя к другому, а прошедшее световое излучение регистрируется решёткой фотодетекторов. Плотность записи в системах оптической памяти может достигать величины 106 бит/мм2. К недостаткам оптической памяти относят большую вероятность порчи отдельных пикселей из-за микродефектов слоя.
Преодолевает этот недостаток систем оптических памяти голографическая память, в которой для записи одного бита информации используется сферическая волна, которая регистрируется на поверхности плоской голограммы, включающей несколько пикселей. Очевидно, что в этом случае вероятность порчи в записи одного бита информации из-за микродефектов в одном пикселе существенно ниже, чем это имеет место в системах оптической памяти. При считывании каждому биту информации в системе голографической памяти соответствует своя интерференционная картина. Записи большого количества битов (странице) соответствует сложная интерференционная картина. Голограмма соответствующая странице памяти занимает площадь 0.2 мм2 и имеет информационную ёмкость в 102 -104 бит.
Существенным ресурсом увеличения плотности записи информации на голограмме является использование не плоских, а объёмных голограмм, позволяющих получить плотность записи в 109 бит/мм2.