Слайд 2ВОЛНОВАЯ ОПТИКА ИНТЕРФЕРЕНЦИЯ СВЕТА
Слайд 3ИНТЕРФЕРЕНЦИЯ СВЕТА – сложение двух (или несколь-ких) когерентных световых волн,
в результате которо-го происходит перераспределение светового потока, при котором в
одних местах возникают максимумы, а в других минимумы интенсивностей света.
Когерентность – согласованное протекание во времени и пространстве нескольких волновых процессов.
Монохроматические волны – неограниченные в про-странстве волны одной и той же частоты (длины волны).
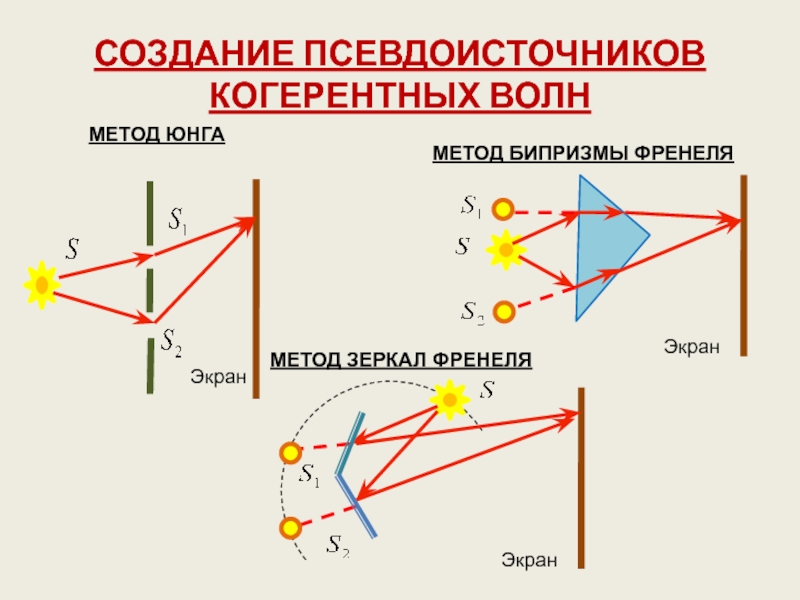
На опыте не наблюдается интерференция света от независимых источников, и приходится прибегать к псевдоисточникам.
Слайд 4СОЗДАНИЕ ПСЕВДОИСТОЧНИКОВ КОГЕРЕНТНЫХ ВОЛН
Слайд 5ИНТЕРФЕРЕНЦИЯ ДВУХ КОГЕРЕНТНЫХ ВОЛН
Пусть две монохроматические волны накладываясь друг на
друга возбуждают в точке колебания одинакового направления.
Под смещением х понимается
напряженность электри-ческого Е или магнитного Н полей. Амплитуда резуль-тирующего колебания:
Так как волны когерентны, то имеет постоян-ное во времени, но своё для каждой точки значение.
Так как интенсивность сигнала пропорциональна квадра-
Слайд 6 ту амплитуды (A²~I), то интенсивность результирующей волны
Там где
, интенсивность , где интенсивность , следовательно, при наложении нескольких когерентных световых волн происходит пространственное перераспределение светового пото-ка, в результате чего в одних местах возникают мини-мумы, а в других максимумы интенсивности. Это явле-ние и будет интерференцией света. Для некогерентных волн разность всё время изменяется, и интен-сивность результирующей волны всюду одинакова, а значит, интерференции не происходит.
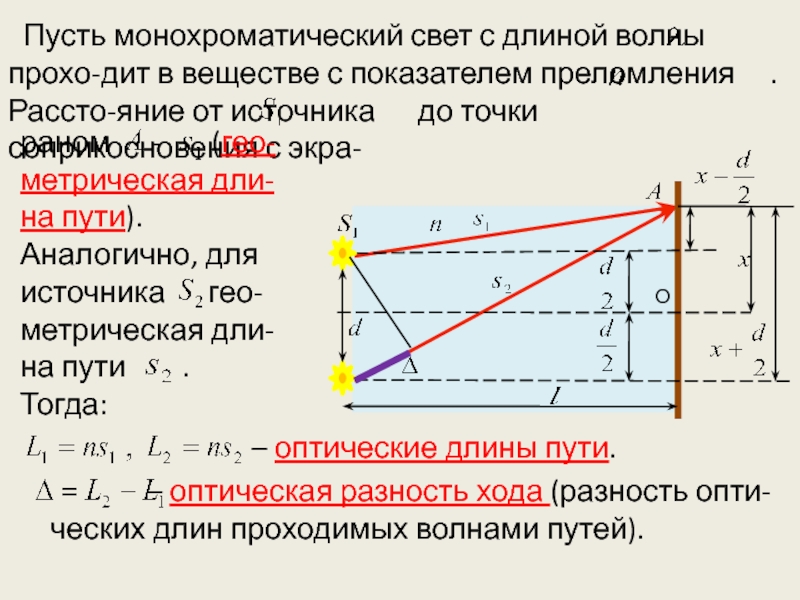
Слайд 7Пусть монохроматический свет с длиной волны прохо-дит в
веществе с показателем преломления . Рассто-яние от источника
до точки соприкосновения с экра-
Тогда:
– оптические длины пути.
– оптическая разность хода (разность опти-ческих длин проходимых волнами путей).
раном - (гео-метрическая дли-на пути). Аналогично, для источника гео-метрическая дли-на пути .
то колебания возбуждённые в точке обе-ими волнами будут происходить в
ОДИНАКОВОЙ фазе. Это: УСЛОВИЕ ИНТЕРФЕРЕНЦИОННОГО МАКСИМУМА.
Если: , то колебания будут проходить в ПРОТИВОФАЗЕ. Это УСЛОВИЕ ИНТЕРФЕРЕНЦИОННОГО МИНИМУМА.
Расчет интерференционной картины для двух источников света можно определить с помощью рисунка ( на пре-дыдущем слайде).
Пусть окружающая среда – вакуум ( ). Когерентные ис-точники света и находятся на расстоянии от экрана и на расстоянии друг от друга ( ).
Точка О находится на экране, на равных расстояниях от обоих источников света.
Слайд 9Интенсивность света в любой точке А экрана, лежащей на расстоянии
от О определяется разностью хода
Так как:
Из этого следует:
Слайд 10Для условия интерференционных максимумов
и минимума найденное значение разности
хода полу-чим:
Расстояние от точки О до интерференционного максимума:
Расстояние от точки
О до интерференционного минимума:
Слайд 11Расстояние между соседними максимумами (или мини-мумами), называемое шириной интерференционной полосы
равно:
не зависит от порядка интерференции (величины
), и является постоянной дл . обратно пропор-циональна , а значит, при большом расстоянии меж-ду источниками, отдельные полосы становятся нераз-личимыми.
Интерференционная картина создаваемая на экране представляет собой чередование темных и светлых полос параллельных друг другу. Главный максимум (соответствующий ) проходит через точку О.
Слайд 12Описанное выше справедливо лишь при освещении эк-рана монохроматическим светом (
). Если исполь-зовать
белый свет, представляющий непрерывный набор волн длиной от 0,39 мкм (фиолетовая граница спектра), до 0,75 мкм (красная граница спектра), то интерферен-ционные максимумы для каждой длины волны будут смещены относительно друг друга и иметь вид радужных полос. Только при максимумы для всех длин волн совпадают, и в середине экрана будет наблюдаться белая полоса, по обе стороны которой будут симметрично рас-полагаться спектрально окрашенные полосы максимумов других порядков (ближе к белой полосе будут находиться участки – фиолетового цвета, далее всего – красного).
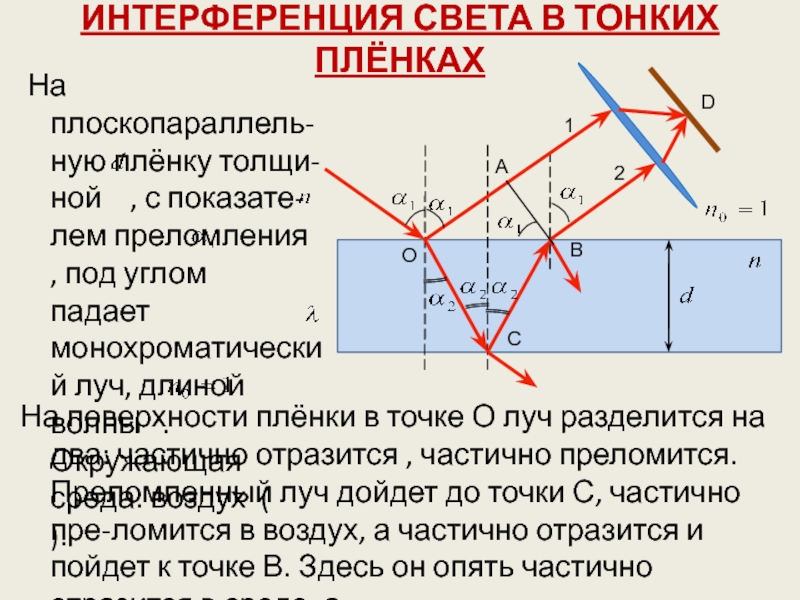
Слайд 13ИНТЕРФЕРЕНЦИЯ СВЕТА В ТОНКИХ ПЛЁНКАХ
На плоскопараллель-ную плёнку толщи-ной
, с показате-лем преломления , под углом
падает монохроматический луч, длиной волны . Окружающая среда: воздух ( ).
На поверхности плёнки в точке О луч разделится на два: частично отразится , частично преломится. Преломленный луч дойдет до точки С, частично пре-ломится в воздух, а частично отразится и пойдет к точке В. Здесь он опять частично отразится в среде, а
Слайд 14 оставшаяся часть преломится выйдя на воздух под углом .
Вышедшие из плёнки лучи 1 и 2 когерентны. Если на
их пути поставить собирающую линзу, то они сойдутся в одной из точек D фокальной плоскости линзы. В результате возникнет интерференционная картина, которая определяется оптической разностью хода между интерферирующими лучами.
Оптическая разность хода возникающая между двумя интерферирующими лучами от точки О до плоскости АВ:
Член уравнения обусловлен потерей полуволны при отражении света от границы раздела. Если , то потеря полуволны произойдет в точке О, и данный
Слайд 15 элемент имеет знак - (минус), если же
, то потеря полуволны произойдет в точке С и
будет иметь знак + (плюс). В данном случае , следовательно:
Слайд 16Разность хода равна:
Условие максимума для точки D
Условие минимума для точки
Слайд 17Интерференционная картина в плоскопараллельных пластинках ( плёнках) определяется величинами
,
, .
Для данных , , каждому наклону лучей соответствует своя интерференционная полоса. Интер-ференционные полосы возникающие возникающие в ре-зультате наложения лучей попадающих на плоско па-раллельную пластину называются – полосами равного наклона. Полосы равного наклона локализованы в бес-конечности. Для их наблюдения используют собираю-щую линзу и экран. Если оптическая ось линзы перпен-дикулярна поверхности пластины, то полосы равного наклона будут иметь вид концентрических колец с центром в фокусе линзы.
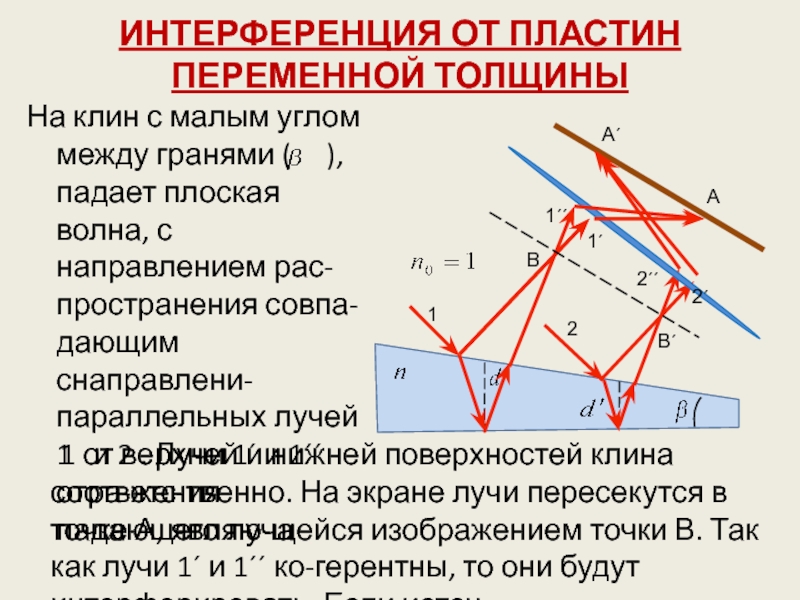
Слайд 18ИНТЕРФЕРЕНЦИЯ ОТ ПЛАСТИН ПЕРЕМЕННОЙ ТОЛЩИНЫ
На клин с малым углом между
гранями ( ), падает плоская волна, с направлением
рас-пространения совпа-дающим снаправлени- параллельных лучей 1 и 2 . Лучи 1´ и 1´´ отра-жения падающего луча
1 от верхней и нижней поверхностей клина соответс-твенно. На экране лучи пересекутся в точке А, являю-щейся изображением точки В. Так как лучи 1´ и 1´´ ко-герентны, то они будут интерферировать. Если источ-
Слайд 19ник волн расположен далеко от поверхности клина и угол
достаточно мал, то оптическая разность хода между этими
лучами определяется по формуле:
Где – толщина клина в месте падения луча 1.
Аналогично, 2´ и 2´´, образовавшиеся за счет деления лу-ча, 2 собираются линзой в точке А´. Разность хода опре-деляется такой же формулой, с заменой на . На экране возникает система интерференционных полос. Каждая из полос возникает за счет отражения от мест пластинки имеющую одинаковую толщину. Интерференционные полосы, возникающие в резуль-тате интерференции от мест одинаковой толщины на-зываются полосами равной толщины.
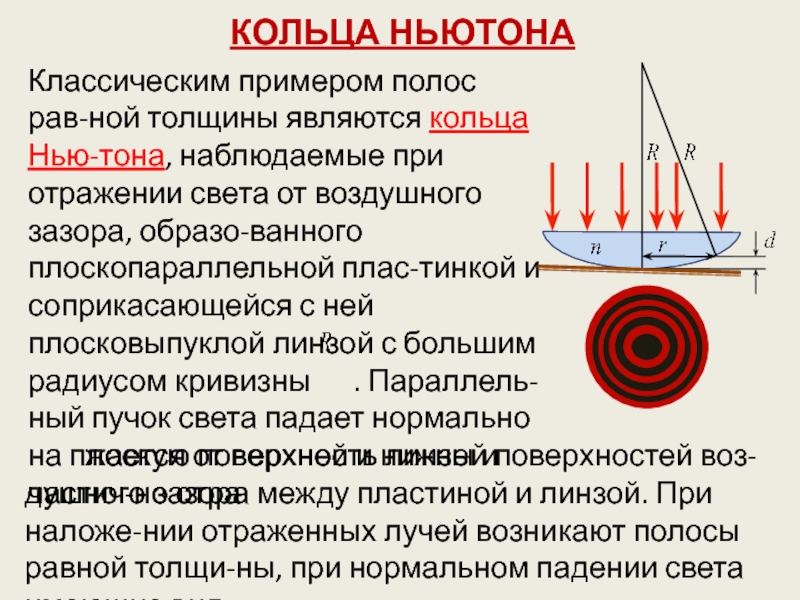
Слайд 20КОЛЬЦА НЬЮТОНА
Классическим примером полос рав-ной толщины являются кольца Нью-тона, наблюдаемые
при отражении света от воздушного зазора, образо-ванного плоскопараллельной плас-тинкой и
соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны . Параллель-ный пучок света падает нормально на плоскую поверхность линзы и частич-но отра
жается от верхней и нижней поверхностей воз-душного зазора между пластиной и линзой. При наложе-нии отраженных лучей возникают полосы равной толщи-ны, при нормальном падении света имеющие вид
Слайд 21концентрических окружностей.
В отраженном свете, при условии что для воздуха
(ваку-ума) , и
(свет падает нормально), с учетом потери полуволны при отражении, оптическая разность хода:
Так как:
То:
Где:
– радиус кривизны линзы
– радиус кривизны окружности, всем точкам которой сопутствует одинаковый зазор .
Слайд 22Так как значение мало, то:
Приравняв это значение к
условиям максимума и мини-мума получим значения радиусов для
-го:
–радиус светлого отраженного кольца
–радиус темного отраженного кольца
Слайд 23Как для полос равного наклона, так и для полос равной
толщины положение максимумов зависит от длины волны .
То есть система темных и светлых полос по-лучается только при освещении монохроматическим светом. При наблюдении в белом свете получается со-вокупность полос, образованных лучами различных длин волн, и интерференционная картина приобретает радужную окраску.
Все рассмотренные выше случаи были приведены для для отраженного света. Интерференцию можно наб-людать и в проходящем свете, однако, при этом не наблюдается потери полуволны. Оптическая разность хода для проходящего и отраженного света отличается на . МАКСИМУМ ИНТЕРФЕРЕНЦИИ В ОТРАЖЕННОМ СВЕТЕ СООТВЕТСТВУЕТ МИНИМУМУ В ПРОХОДЯЩЕМ.
Слайд 24ПРИМЕНЕНИЕ ИНТЕРФЕРЕНЦИИ СВЕТА
Явление интерференции обусловлено волновой приро-дой света, его количественные
характеристики зависят от длины волны . Это явление
применяется для подтвер-ждения волновой природы света, для измерения длин волн (интерференционная спектроскопия), для проведе-ния иных высокоточных измерений, (например контроля чистоты обработки поверхностей), с помощью приборов – интерферометров. Кроме того явление интерференции используется для улучшения качества оптических прибо-ров(просветления оптики) и получения высокоотража-ющих покрытий.
Прохождение света через каждую преломляющую по-верхность линзы (например, при прохождении границы
Слайд 25воздух-стекло, при показателе преломления стекла рав-ном
), сопровождается отражением примерно 4% падающего потока света.
Так как в оптических при-борах много линз, то велико и число отражений, а зна-
жет быть нежелательным.
Для устранения этого недостатка и используют просвет-ление оптики. На свободную поверхность линз наносят плёнку с показателем преломления меньшим чем у линзы . При отражении света от границ просвет-
воздух
Просветляющий слой
стекло
чит и потерь в световом потоке. Это приводит к резкому ослаб-лению светосилы оптического прибора. Помимо этого, отраже-ние от поверхностей приводит к возникновению бликов, что мо-
Слайд 26вляющего слоя возникает интерференция между луча-ми 1´ и 2´ .
Толщину плёнки , показатели преломле-ния стекла
и плёнки можно подобрать так, чтобы интерферирующие лучи гасили друг друга. Их амплиту-ды должны быть одинаковы, а оптическая разность хо-да равна . Амплитуды будут равны, если выполняется условие .
Показатели преломления удовлетворяют условию , значит потеря полуволны проис-ходит на обеих поверхностях просветляющего слоя, и , при нормальном падении света ( ), условие минимума:
– оптическая толщина плёнки
Слайд 27Обычно принимают , следовательно:
Чаще
всего выбирается наиболее восприимчивая для глаза длина волны
мкм. Объективы с просвет-ленные оптикой кажутся зелеными или голубыми.
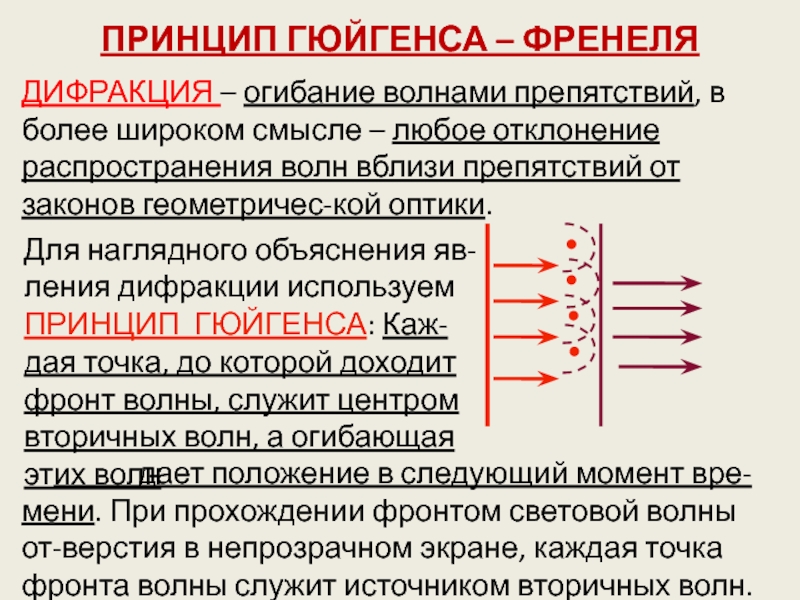
Слайд 29ПРИНЦИП ГЮЙГЕНСА – ФРЕНЕЛЯ
ДИФРАКЦИЯ – огибание волнами препятствий, в
более широком смысле – любое отклонение распространения волн вблизи препятствий
от законов геометричес-кой оптики.
дает положение в следующий момент вре-мени. При прохождении фронтом световой волны от-верстия в непрозрачном экране, каждая точка фронта волны служит источником вторичных волн.
Для наглядного объяснения яв-ления дифракции используем ПРИНЦИП ГЮЙГЕНСА: Каж-дая точка, до которой доходит фронт волны, служит центром вторичных волн, а огибающая этих волн
Слайд 30 Построив огибающую вторичных волн, можно заме-тить, что новый фронт
волны заходит в область геоме-трической тени, то есть волна огибает
края отверстия.
Принцип Гюйгенса решает задачу лишь о направлении волнового фронта, но не рассматривает вопрос об ам-плитудах и интенсивностях волн распространяющихся по разным направлениям.
Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.
ПРИНЦИП ГЮЙГЕНСА – ФРЕНЕЛЯ: световая волна воз-буждаемая каким либо источником S может быть представлена как результат суперпозиции когерентных вторичных волн, излучаемых вторичными источниками.
Слайд 31МЕТОД ЗОН ФРЕНЕЛЯ ПРЯМОЛИНЕЙНОЕ РАСПРОСТРАНЕНИЕ СВЕТА
Френель решил задачу о прямолинейном
распростране-нии света, рассмотрев взаимную интерференцию вто-ричных волн.
Найдем в точке М
амплитуду световой волны, распрост-раняющейся в однородной среде из точечного источни-ка S.
Фронт световой волны предста-вляет собой сферу с центром в точке S. Заменим действие ис-точника S действием вообража-емых источников на вспомога-тельной поверхности F, являю-
Слайд 32щейся поверхностью фронта волны идущей из S. По-верхность F разбита
на кольцевые зоны такого разме-ра, что расстояния от краев зоны
до М отличаются на ( ).
Так как в колебания соседних зон проходят до точки М расстояния отличающиеся друг от друга на , то в М они приходят в противоположной фазе, и при наложе-нии будут взаимно ослаблять друг друга.
Результирующая амплитуда колебания в точке М:
Где:
– амплитуды возбуждаемые соответственно 1, 2, 3,…, m зонами.
Слайд 33Внешняя граница зоны выделяет сегмент высотой
и радиусом где:
Учитывая что
и получим:
При небольших значениях , площади зон Френеля можно считать одинаковыми, и построение зон Фре-
неля разбивает волновую по-верхность на равные зоны.
Действие отдельных зон Фре-неля в точке М тем меньше, чем больше угол , и значит:
Слайд 34В качестве допустимого предположения можно считать, что амплитуда колебания
от -ной зоны Френеля равна среднему
арифметическому от примыкающих к ней зон:
Следовательно суммарная амплитуда в точке М равна:
(выражения в скобках равны нулю а последнее значение ничтожно мало).
Амплитуда создаваемая в произвольной точке М сфери-ческой волновой поверхностью, равна половине амп-литуды создаваемой центральной зоной и действие всей волновой поверхности сводится к действию мало-го участка центральной зоны.
небольших будет справедливо, что
. Подставив значение получим:
– радиус -го участка зоны Френеля
– расстояние от источника S до волновой поверхности
– расстояние от волновой поверхности до рассматри-ваемой точки
Распространение света от источника S до точки наблю-дения М происходит так, будто световой поток распро-страняется внутри очень узкого канала вдоль оси SM, то есть ПРЯМОЛИНЕЙНО. Таким образом принцип Гюйген-са-Френеля позволяет объяснить прямолинейное рас-пространение света в однородной среде.
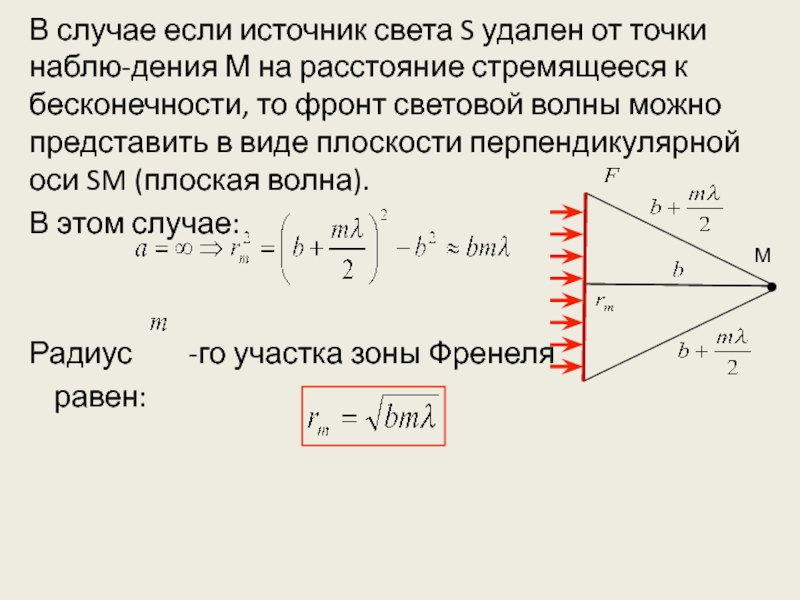
Слайд 36В случае если источник света S удален от точки наблю-дения
М на расстояние стремящееся к бесконечности, то фронт световой волны
можно представить в виде плоскости перпендикулярной оси SM (плоская волна).
В этом случае:
Радиус -го участка зоны Френеля
равен:
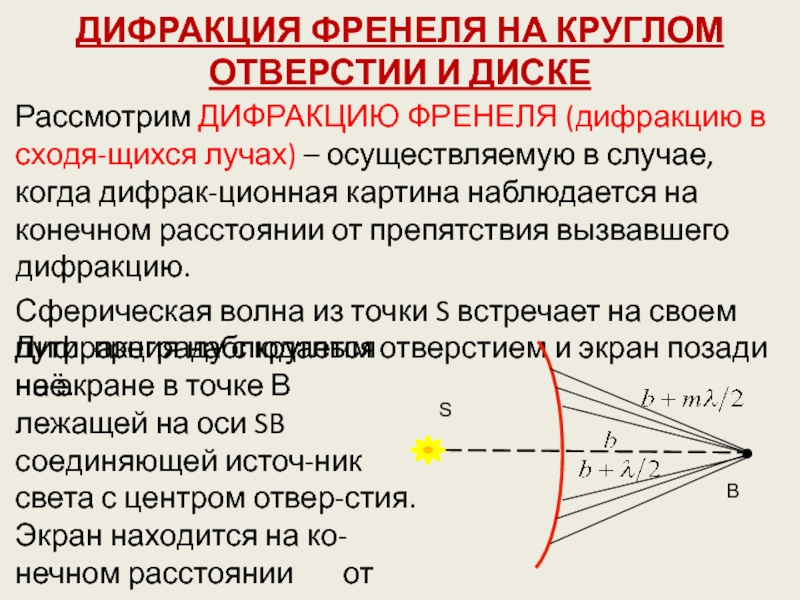
Слайд 37ДИФРАКЦИЯ ФРЕНЕЛЯ НА КРУГЛОМ ОТВЕРСТИИ И ДИСКЕ
Рассмотрим ДИФРАКЦИЮ ФРЕНЕЛЯ (дифракцию
в сходя-щихся лучах) – осуществляемую в случае, когда дифрак-ционная картина
наблюдается на конечном расстоянии от препятствия вызвавшего дифракцию.
Сферическая волна из точки S встречает на своем пути преграду с круглым отверстием и экран позади неё.
Дифракция наблюдается на экране в точке В лежащей на оси SB соединяющей источ-ник света с центром отвер-стия. Экран находится на ко-нечном расстоянии от отверстия.
Слайд 38Разобьём открытую часть волновой поверхности на зоны Френеля. Амплитуда результирующего
колебания возбуждаемого в точке В всеми зонами будет равна:
Где
знак «+» соответствует нечетным , знак «–» соответ-ствует четным значениям предельной открытой зоны Френеля.
Когда отверстие открывает НЕЧЕТНОЕ количество зон Френеля, то амплитуда (интенсивность) света в точке В будет БОЛЬШЕ, чем при свободном распространении волны, если ЧЕТНОЕ, то амплитуда в точке В равна НУЛЮ.
Слайд 39Если в отверстие укладывается одна зона Френеля, то её амплитуда
в точке В будет равна:
То есть в два раза больше
чем при свободном распро-странении волны (соответственно интенсивность больше в четыре раза).
Дифракционная картина вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в В (если четное, то в центре будет темное пятно, если нечетное, то центр светлый), причем интенсивность мак-симумов убывает по мере удаления от точки В.
Число зон Френеля укладывающихся в отверстие зависит от его диаметра. Если он большой, то , и в резуль-тате , то есть такая же как и при открытом вол-новом фронте. Дифракционная картина отсутствует, свет распространяется прямолинейно.
Слайд 40Если световая волна распространяющаяся от точечного источника встречает на своем
пути диск, то закрытый диском участок фронта необходимо исключить из
рас-смотрения и начинать строить зоны Френеля с концов диска. Если диск закрывает зон Френеля, то ампли-туда колебания в точке В равна:
В точке В всегда наблюдается ин-терференционный максимум (свет-лое пятно), соответствующий поло-вине действия первой открытой зо-ны Френеля. Он окружен чередую-щимися темными светлыми поло-сами.
Слайд 41 Интенсивность максимумов убывает по мере уве-личения расстояния от центра картины.
Интенсивность
центрального максимума с ростом раз-меров диска уменьшается. При большом диаметре
диска дифракционной картиной можно пренебречь, и считать свет распространяющимся прямолинейно.