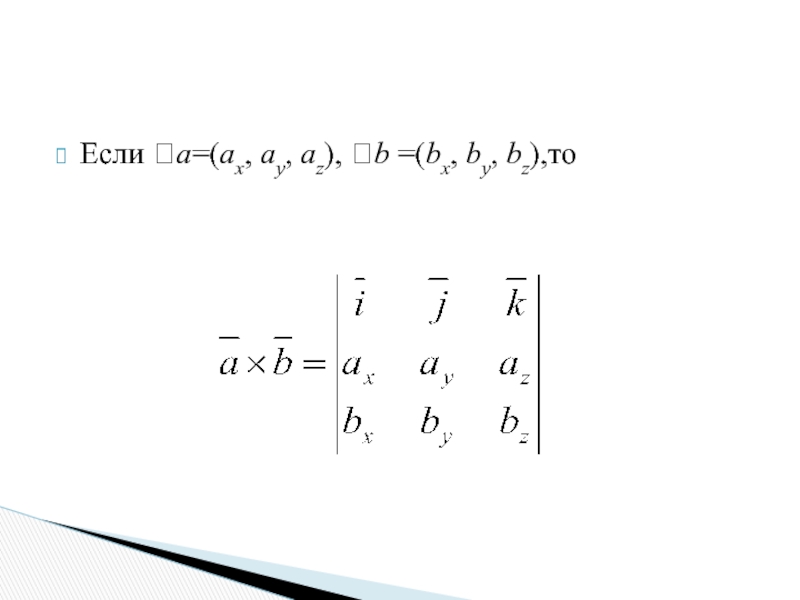Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ
Содержание
- 1. ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ
- 2. вектор;длина вектора;свободные векторы;равные векторы;нулевой вектор;коллинеарные векторы;компланарные векторы;n
- 3. Слайд 3
- 4. Слайд 4
- 5. Равные векторы длины векторов равны;расположены на одной или параллельных прямых;сонаправленные
- 6. Нулевой вектор
- 7. Взаимное расположение векторов
- 8. Взаимное расположение векторов
- 9. Слайд 9
- 10. Линейные операции над векторами
- 11. Слайд 11
- 12. Слайд 12
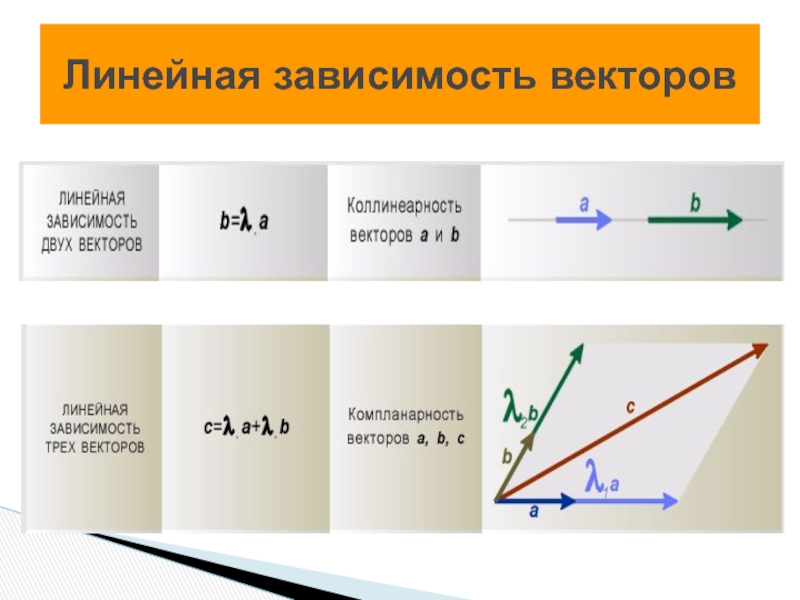
- 13. Линейная зависимость векторов
- 14. Слайд 14
- 15. Декартова система координат
- 16. Слайд 16
- 17. Основные формулыЕсли вектор
- 18. №1. Найти длины диагоналей параллелограмма, построенного на
- 19. Слайд 19
- 20. скалярное произведение двух векторов;векторное произведение двух векторов;смешанное произведение трех векторовНЕЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
- 21. Скалярное произведение двух векторов
- 22. Слайд 22
- 23. Если a=(ax, ay, az), b =(bx, by, bz),тоКоординатная форма скалярного произведения
- 24. Слайд 24
- 25. Векторное произведение двух векторов
- 26. Слайд 26
- 27. Если a=(ax, ay, az), b =(bx, by, bz),то
- 28. Слайд 28
- 29. Смешанное произведение трех векторов
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Спасибо за внимание
- 37. Скачать презентанцию
вектор;длина вектора;свободные векторы;равные векторы;нулевой вектор;коллинеарные векторы;компланарные векторы;n – мерный вектор и его координаты;векторное пространство;линейная комбинация векторов;линейно-зависимая и линейно-независимая система векторов;базис векторного пространства;проекция вектора на ось;проекция точки на ось;координаты вектора в ДСК;направляющие
Слайды и текст этой презентации
Слайд 1ВЕКТОРЫ И ДЕЙСТВИЯ НАД НИМИ
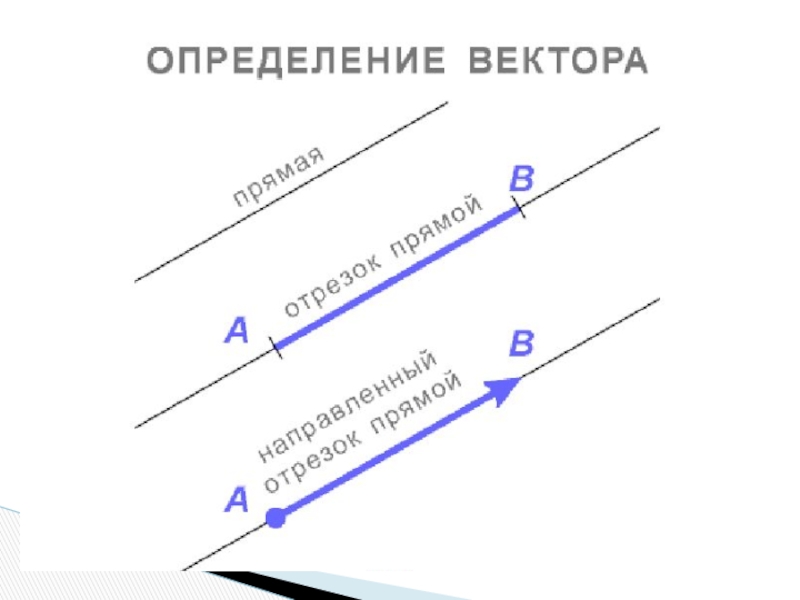
Основные понятия.
Линейные операции над векторами.
Векторное пространство.
Разложение
вектора по базису.
Слайд 2вектор;
длина вектора;
свободные векторы;
равные векторы;
нулевой вектор;
коллинеарные векторы;
компланарные векторы;
n – мерный вектор
и его координаты;
векторное пространство;
линейная комбинация векторов;
линейно-зависимая и линейно-независимая система векторов;
базис
векторного пространства;проекция вектора на ось;
проекция точки на ось;
координаты вектора в ДСК;
направляющие косинусы вектора
Основные понятия
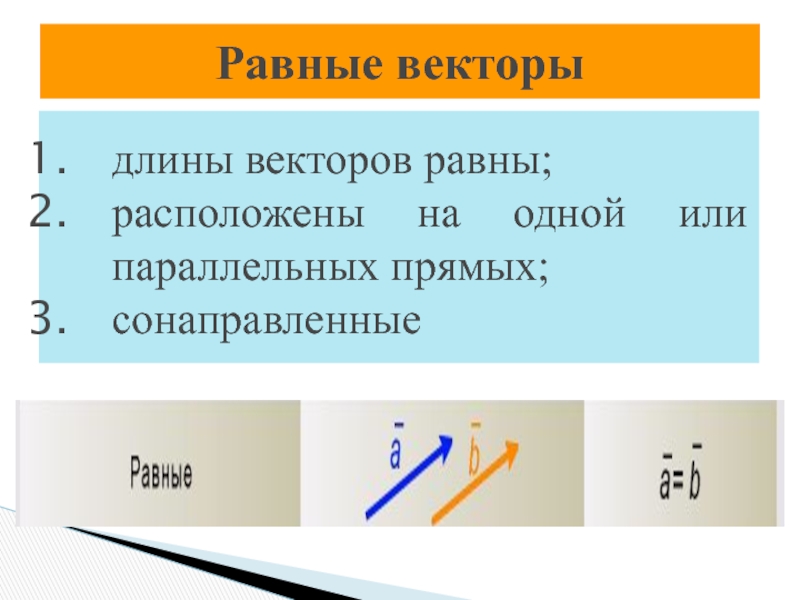
Слайд 5Равные векторы
длины векторов равны;
расположены на одной или параллельных прямых;
сонаправленные
Слайд 17Основные формулы
Если вектор
, то:
;
;
, где - угол между вектором a и положительным направлением оси l
Слайд 18№1. Найти длины диагоналей параллелограмма, построенного на векторах:
= (3; -5; 8) и
= (-1; 1; -4).
№2. Вектор , заданный в трехмерном пространстве составляет с координатными осями Ох и Оу углы =60˚, β=120˚. Вычислить его координаты если a = 2.
№3. Даны четыре точки , , . , . Выяснить, коллинеарны ли векторы и ?
Примеры:
Слайд 20скалярное произведение двух векторов;
векторное произведение двух векторов;
смешанное произведение трех векторов
НЕЛИНЕЙНЫЕ
ОПЕРАЦИИ
НАД ВЕКТОРАМИ
Слайд 22
(переместительное);
(сочетательное);(распределительное);
;
;
Свойства скалярного произведения
Слайд 30
;
если три данных вектора компланарны, то (и наоборот);
;
;
если три вектора заданы координатами a=(x1; y1; z1), b=(x2; y2; z2), c=(x3; y3; z3), то смешанное произведение вычисляется по формуле:
Свойства смешанного произведения