УРАВНЕНИЯ МАКСВЕЛЛА

1-ое уравнение Максвелла.
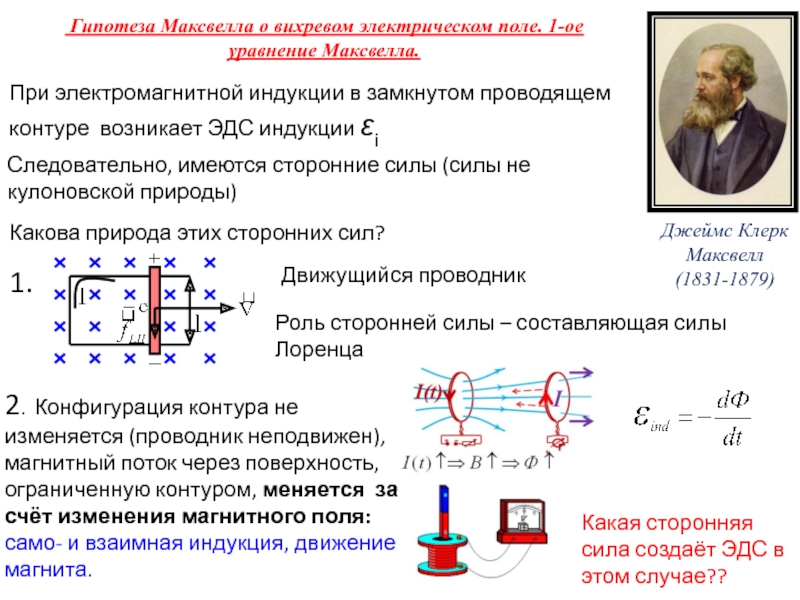
При электромагнитной индукции в замкнутом проводящем контуре возникает

Следовательно, имеются сторонние силы (силы не кулоновской природы)

Какова природа этих сторонних сил?

Движущийся проводник

Роль сторонней силы – составляющая силы Лоренца

2. Конфигурация контура не изменяется (проводник неподвижен), магнитный поток через поверхность, ограниченную контуром, меняется за счёт изменения магнитного поля: само- и взаимная индукция, движение магнита.

1.

Какая сторонняя сила создаёт ЭДС в этом случае??

Магнитный поток через поверхность, ограниченную контуром, меняется за счёт изменения

Какая сторонняя сила создаёт ЭДС в этом случае εi??

Максвелл:
изменяющееся во времени магнитное поле приводит к возникновению вихревого (не потенциального) электрического поля, существование которого не зависит от наличия проводников

– сила, действующая со стороны вихревого электрического поля на
точечный заряд q, помещенный в данную точку.

- сторонняя сила

по аналогии с определением напряженности электростатического поля

В проводнике, помещенном в вихревое электрическое поле, возникает индукционный ток - движение свободных носителей заряда под действием сил вихревого электрического поля.

контур ℓ – не обязательно проводящий!
Это может быть

Переменное магнитное поле приводит к появлению вихревого электрического поля независимо от того, в какой среде это происходит.

Например, если магнитное поле меняется в вакууме, то вихревое электрическое поле существует в вакууме (как и кулоновское)

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
ПОТЕНЦИАЛЬНОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Особенности вихревого электрического поля
Источником вихрев. электр. поля

= 0

Нельзя ввести потенциал

ВСЕГДА:

Источником потенц. электр. поля являются электр. заряды

≠ 0

Теорема Гаусса

Поле характеризуется потенциалом

Силовые линии вихревого электр. поля замкнуты (не имеют начала и конца)

Силовые линии потенц. электр. поля начинаются и заканчиваются на электрических зарядах

перемещения вдоль замкнутого контура
1-ое уравнение Максвелла
+
3-е уравнение Максвелла

тока
Максвелл:
ТОК СМЕЩЕНИЯ (в случае однородного поля)
ПЛОТНОСТЬ ТОКА СМЕЩЕНИЯ

смещения совпадают
Рассмотрим разаряд плоского конденсатора:

и плотность тока смещения

Поле однородно

Таким образом, линии тока проводимости в проводах на границах обкладок непрерывно переходят в линии тока смещения внутри конденсатора (независимо от того заряжается или разряжается конденсатор).

же, как и магнитное поле эквивалентного тока проводимости.

магнитное поле
Лампочка горит!!

индукции:
Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна

МАКСВЕЛЛ: полный ток

Постоянный ток

Плотность полного тока

Равноценны в отношении создания магнитного поля

Плотность тока проводимости

Плотность тока смещения

Из всех свойств, присущих току присуще лишь одно – создавать в окружающем пространстве магнитное поле

и ток проводимости.
2-е уравнение Максвелла
Теорема о циркуляции вектора магнитной индукции:
проводящая

2-ое уравнение Максвелла

среды, в том числе для диэлектрика, вакуума или неоднородной среды,

Например, в случае вакуума (воздуха)

поля по произвольному контуру, равна «минус» скорости изменения магнитного потока

циркуляция вектора напряжённости магнитного поля по произвольному контуру равна алгебраической сумме токов проводимости и токов смещения, охватываемых этим контуром (теорема о циркуляции для м.п. +.ток смещения)

поток вектора электрической индукции через
произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности (теорема Гаусса – закон Кулона)).

Поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю (отсутствие магнитных зарядов)

Дополнив основные факты из области электромагнетизма установлением магнитных действий токов смещения, Максвелл написал систему фундаментальных уравнений электродинамики.

основные аксиомы электродинамики полученные путём обобщения опытных фактов (их нельзя

Из уравнений Максвелла следует возможность существования электромагнитных волн.

составляют полной системы уравнений электромагнитного поля.
Уравнения Максвелла не содержат данных

Уравнения Максвелла следует дополнить соотношениями, характеризующими свойства среды – «материальными уравнениями»

Если электромагнитное поле
не слишком сильное,
не меняется слишком быстро в о времени и резко в пространстве,
отсутствуют ферромагнетики и сегнетоэлектрики,

материальные уравнения

Остроградского-Гаусса
Т. Стокса
Т. Остроградского - Гаусса
где
Дивергенция векторного поля, скаляр
Ротор векторного

S – поверхность ограниченная контуром l

V – объём внутри замкнутой поверхности S

Фарадея (1-е ур-е Максвелла)
Т. О.– Г.
Т. Стокса