Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 8
Содержание
- 1. Лекция 8
- 2. Дерево двоичного поискаДеревья двоичного поиска – способ
- 3. Поиск элемента-573232831452562426Содержит ли дерево заданное значение (да/нет)Нерекурсивный
- 4. Простое добавление элемента-573232831452562426Нерекурсивный вариант.TreeNode* add(TreeNode*root, int x){
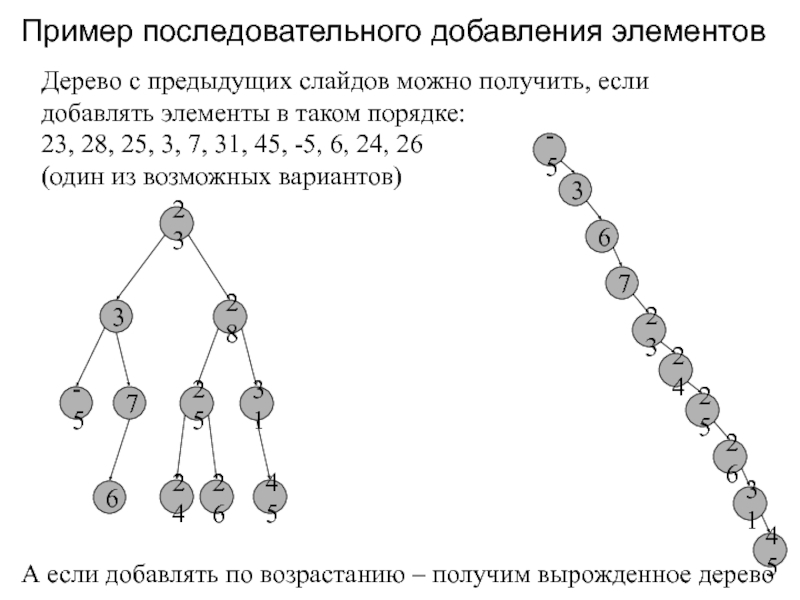
- 5. Пример последовательного добавления элементов23Дерево с предыдущих слайдов
- 6. Поиск максимального или минимального значения23328-5725314562426Начинаем с корня
- 7. Поиск следующего элемента23328-5725314562426Найдём элемент. Если у него
- 8. Варианты простого удаления элементаСлучай 1. Удаляемый элемент
- 9. Случай 1. Удаляемый элемент является листом – то есть, не имеет потомков.23328-5725314562426Удаление элемента 26.23328-57253145624
- 10. Случай 2. У удаляемого элемента один потомок.23328-5725314562426Удаление элемента 7. Потомок (6) ставится на место удаляемого23328-562531452426
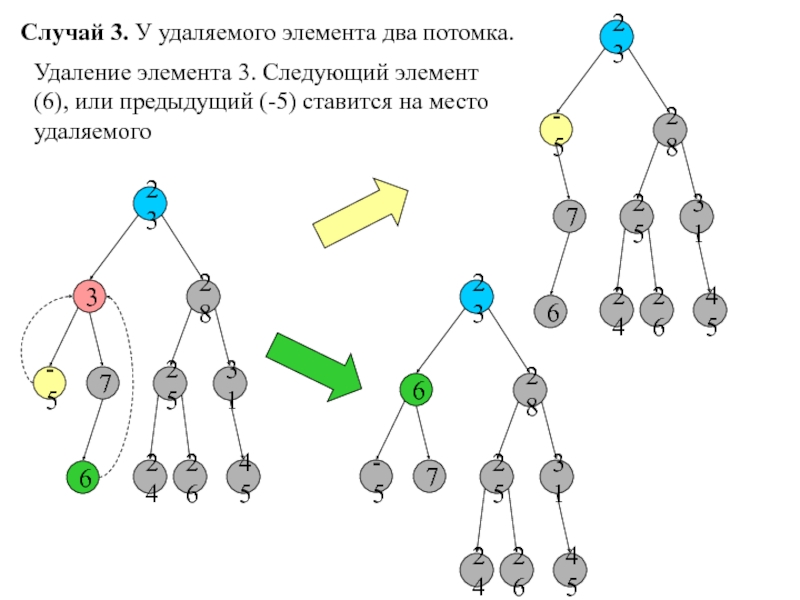
- 11. Случай 3. У удаляемого элемента два потомка.23328-5725314562426Удаление
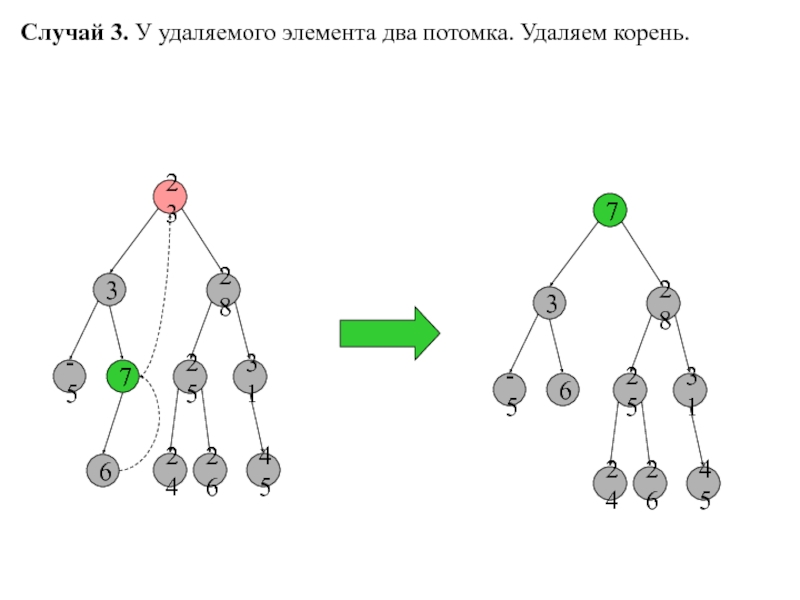
- 12. Случай 3. У удаляемого элемента два потомка. Удаляем корень.23328-57253145624267328-562531452426
- 13. Пример последовательного добавления элементов23328-5725314562426Дерево с предыдущих слайдов
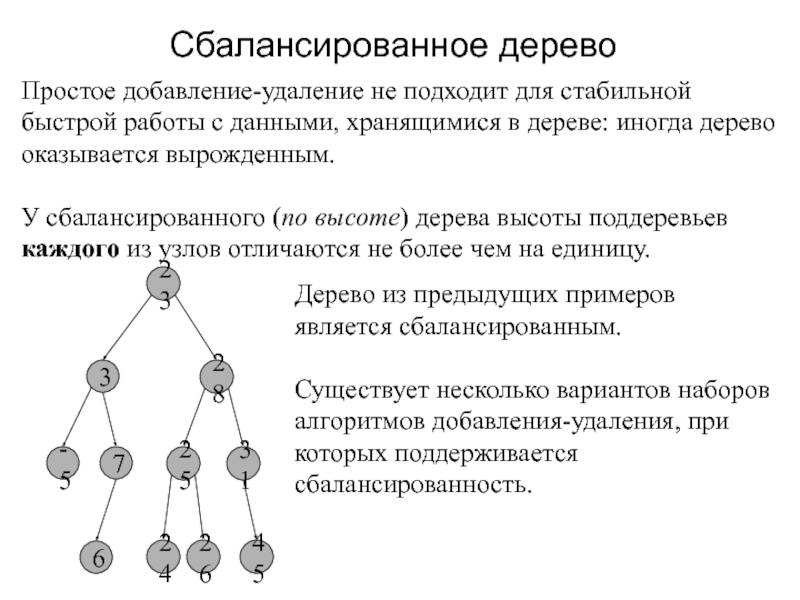
- 14. Сбалансированное деревоПростое добавление-удаление не подходит для стабильной
- 15. Свойства: количество элементовN-1N-2N уровнейСбалансированное дерево с N
- 16. АВЛ-деревоОдин из вариантов сбалансированного (по высоте) дерева,
- 17. Добавление элементаrhLhRНа схеме, r – корень (root),
- 18. Балансировка 1 – «малое вращение»r23A1Элемент был добавлен
- 19. Балансировка 2 – «большое вращение»r24A1Элемент был добавлен
- 20. Пример11212323123142314524135241356423561
- 21. 42356174235617423561784235617894235617894235617891042356178910
- 22. АВЛ – дерево, комментарииБалансировка при добавлении в
- 23. Красно-чёрное деревоRudolf Bayer1972, «Symmetric Binary B-Trees. Data
- 24. Красно-чёрное деревоПравила1. Каждый узел либо красный, либо
- 25. Балансировки при добавленииРаботают рекурсивно. Если текущий узел
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 8
Сбалансированное дерево двоичного поиска. АВЛ-дерево, красно-чёрное дерево.
Основы алгоритмизации и
программирования
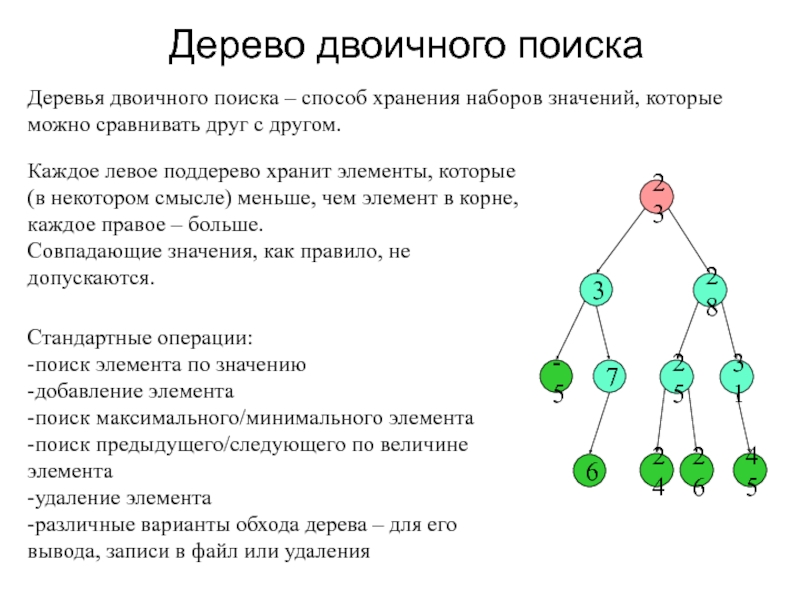
Слайд 2Дерево двоичного поиска
Деревья двоичного поиска – способ хранения наборов значений,
которые можно сравнивать друг с другом.
-5
7
3
23
28
31
45
25
6
24
26
Каждое левое поддерево хранит элементы,
которые (в некотором смысле) меньше, чем элемент в корне, каждое правое – больше.Совпадающие значения, как правило, не допускаются.
Стандартные операции:
-поиск элемента по значению
-добавление элемента
-поиск максимального/минимального элемента
-поиск предыдущего/следующего по величине элемента
-удаление элемента
-различные варианты обхода дерева – для его вывода, записи в файл или удаления
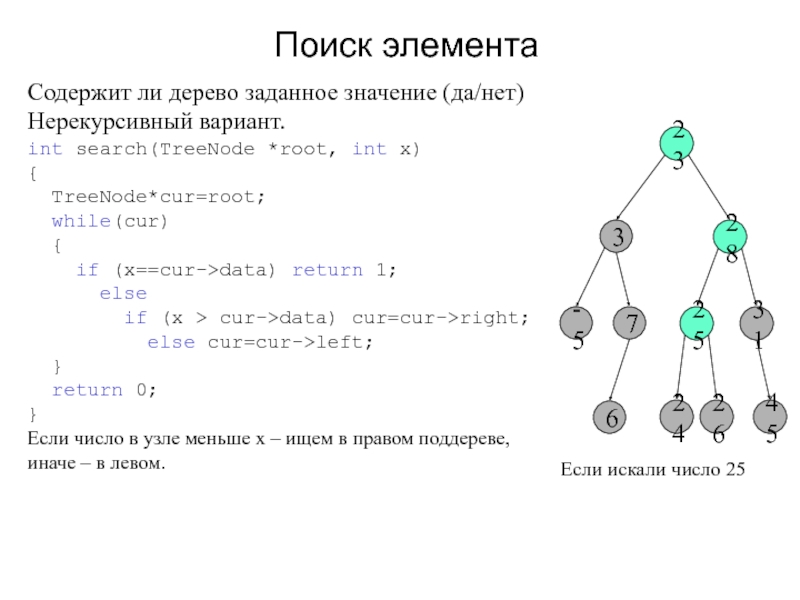
Слайд 3Поиск элемента
-5
7
3
23
28
31
45
25
6
24
26
Содержит ли дерево заданное значение (да/нет)
Нерекурсивный вариант.
int search(TreeNode *root,
int x)
{
TreeNode*cur=root;
while(cur)
{
if (x==cur->data) return 1;
elseif (x > cur->data) cur=cur->right;
else cur=cur->left;
}
return 0;
}
Если число в узле меньше x – ищем в правом поддереве, иначе – в левом.
Если искали число 25
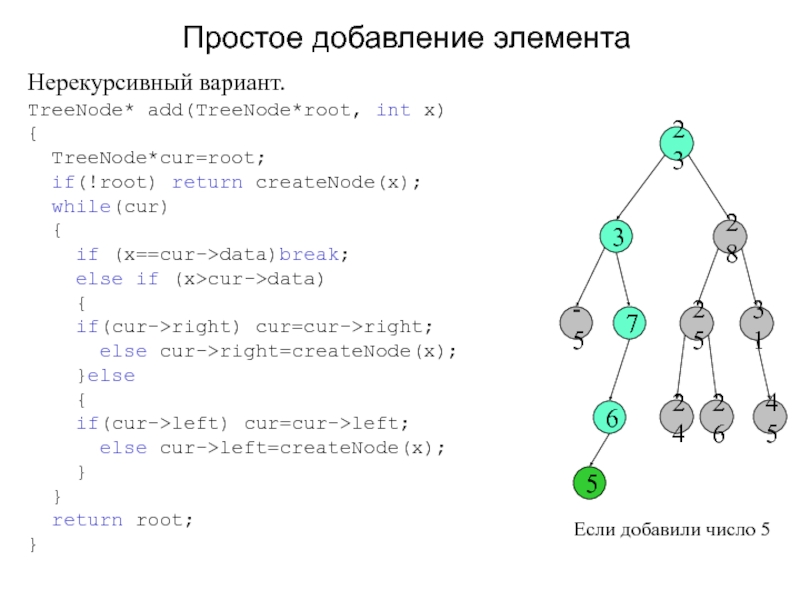
Слайд 4Простое добавление элемента
-5
7
3
23
28
31
45
25
6
24
26
Нерекурсивный вариант.
TreeNode* add(TreeNode*root, int x)
{
TreeNode*cur=root;
if(!root) return
createNode(x);
while(cur)
{
if (x==cur->data)break;
else if (x>cur->data)
{if(cur->right) cur=cur->right;
else cur->right=createNode(x);
}else
{
if(cur->left) cur=cur->left;
else cur->left=createNode(x);
}
}
return root;
}
5
Если добавили число 5
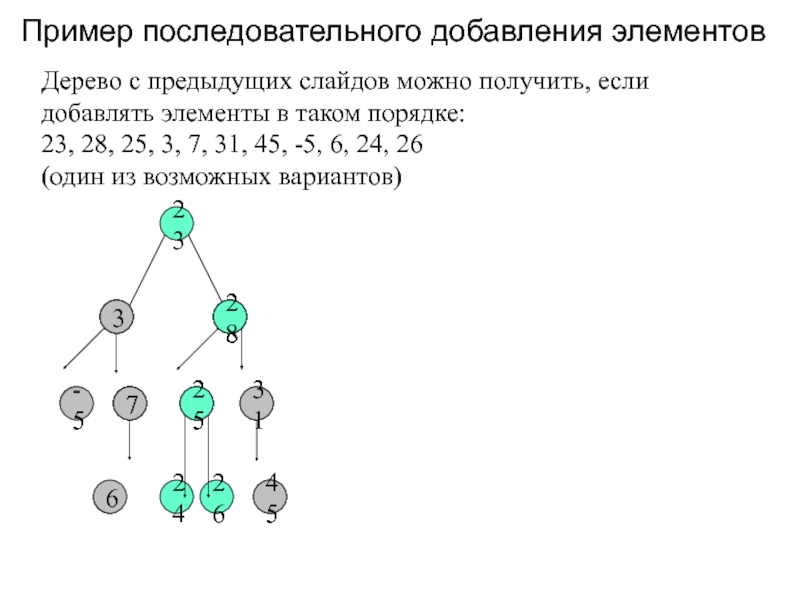
Слайд 5Пример последовательного добавления элементов
23
Дерево с предыдущих слайдов можно получить, если
добавлять элементы в таком порядке:
23, 28, 25, 3, 7, 31,
45, -5, 6, 24, 26(один из возможных вариантов)
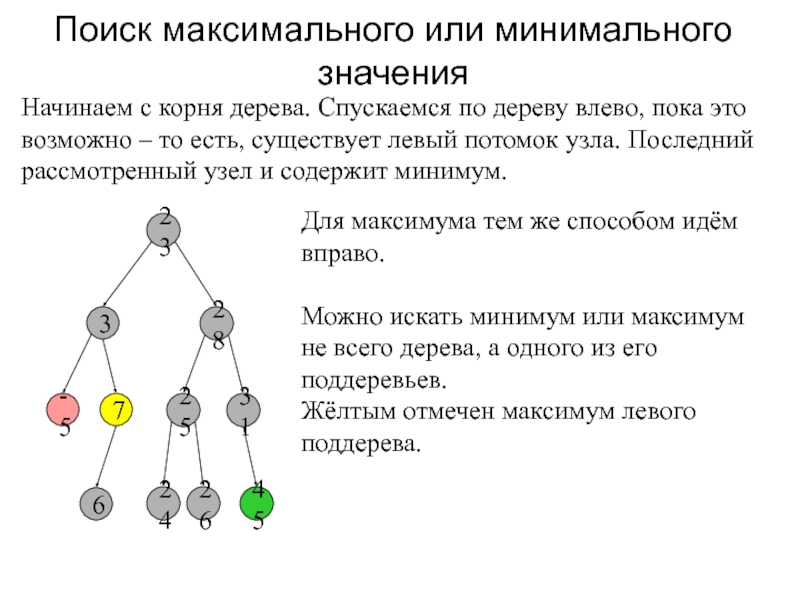
Слайд 6Поиск максимального или минимального значения
23
3
28
-5
7
25
31
45
6
24
26
Начинаем с корня дерева. Спускаемся по
дереву влево, пока это возможно – то есть, существует левый
потомок узла. Последний рассмотренный узел и содержит минимум.Для максимума тем же способом идём вправо.
Можно искать минимум или максимум не всего дерева, а одного из его поддеревьев.
Жёлтым отмечен максимум левого поддерева.
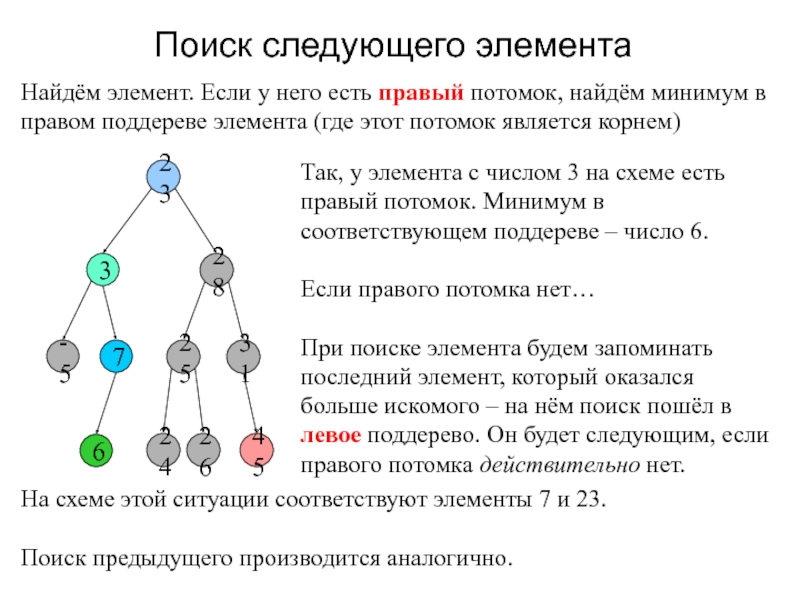
Слайд 7Поиск следующего элемента
23
3
28
-5
7
25
31
45
6
24
26
Найдём элемент. Если у него есть правый потомок,
найдём минимум в правом поддереве элемента (где этот потомок является
корнем)Так, у элемента с числом 3 на схеме есть правый потомок. Минимум в соответствующем поддереве – число 6.
Если правого потомка нет…
При поиске элемента будем запоминать последний элемент, который оказался больше искомого – на нём поиск пошёл в левое поддерево. Он будет следующим, если правого потомка действительно нет.
На схеме этой ситуации соответствуют элементы 7 и 23.
Поиск предыдущего производится аналогично.
Слайд 8Варианты простого удаления элемента
Случай 1. Удаляемый элемент является листом –
то есть, не имеет потомков.
Решение: В переменную left или right
элемента-отца, где был указатель на удаляемый, записать NULL.Случай 2. У удаляемого элемента один потомок.
Решение: В переменную left или right элемента-отца, где был указатель на удаляемый, записать адрес потомка удаляемого.
Случай 3. У удаляемого элемента два потомка.
Решение: Найти и «отцепить» любой из элементов: содержащий предыдущее или следующее значение. Поставить его на место удаляемого.
Сам найденный элемент стирается из памяти.
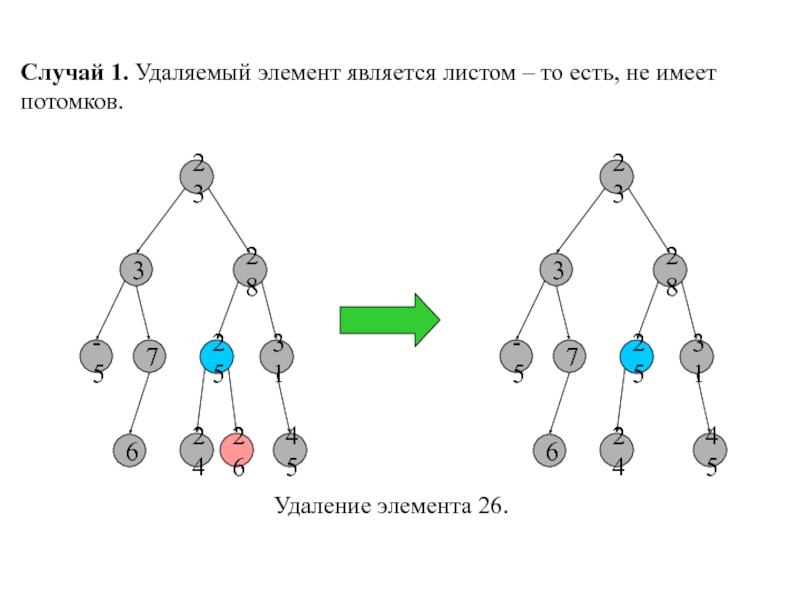
Слайд 9Случай 1. Удаляемый элемент является листом – то есть, не
имеет потомков.
23
3
28
-5
7
25
31
45
6
24
26
Удаление элемента 26.
23
3
28
-5
7
25
31
45
6
24
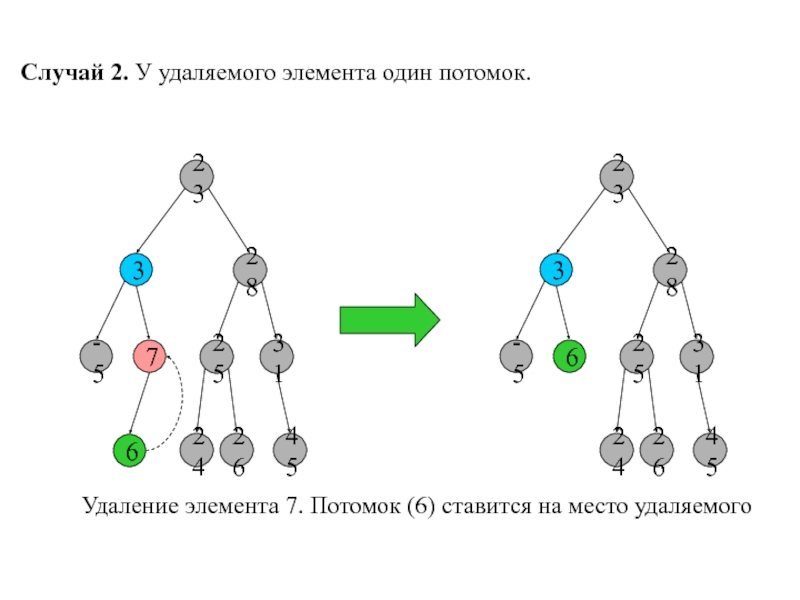
Слайд 10Случай 2. У удаляемого элемента один потомок.
23
3
28
-5
7
25
31
45
6
24
26
Удаление элемента 7. Потомок
(6) ставится на место удаляемого
23
3
28
-5
6
25
31
45
24
26
Слайд 11Случай 3. У удаляемого элемента два потомка.
23
3
28
-5
7
25
31
45
6
24
26
Удаление элемента 3. Следующий
элемент (6), или предыдущий (-5) ставится на место удаляемого
23
-5
28
7
25
31
45
24
26
23
6
28
-5
7
25
31
45
24
26
6
Слайд 12Случай 3. У удаляемого элемента два потомка. Удаляем корень.
23
3
28
-5
7
25
31
45
6
24
26
7
3
28
-5
6
25
31
45
24
26
Слайд 13Пример последовательного добавления элементов
23
3
28
-5
7
25
31
45
6
24
26
Дерево с предыдущих слайдов можно получить, если
добавлять элементы в таком порядке:
23, 28, 25, 3, 7, 31,
45, -5, 6, 24, 26(один из возможных вариантов)
А если добавлять по возрастанию – получим вырожденное дерево
-5
3
6
7
23
24
25
26
31
45
Слайд 14Сбалансированное дерево
Простое добавление-удаление не подходит для стабильной быстрой работы с
данными, хранящимися в дереве: иногда дерево оказывается вырожденным.
У сбалансированного (по
высоте) дерева высоты поддеревьев каждого из узлов отличаются не более чем на единицу.23
3
28
-5
7
25
31
45
6
24
26
Дерево из предыдущих примеров является сбалансированным.
Существует несколько вариантов наборов алгоритмов добавления-удаления, при которых поддерживается сбалансированность.
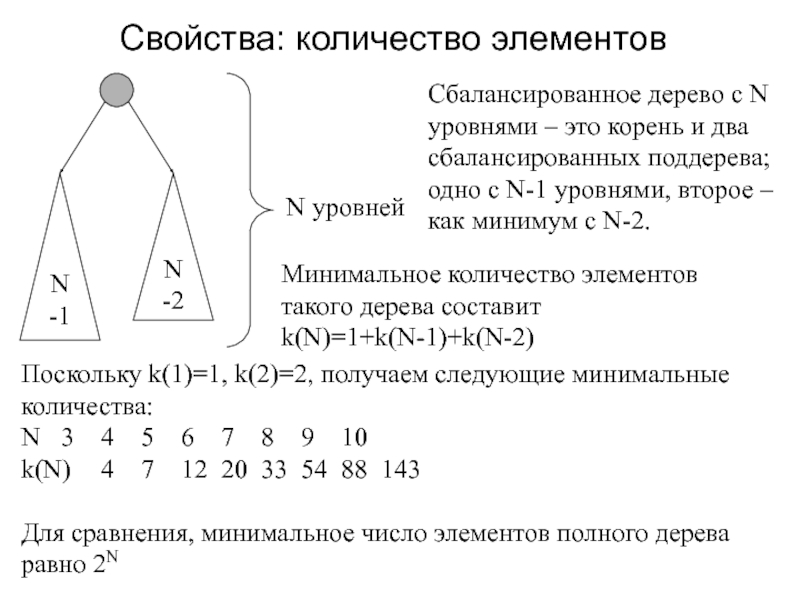
Слайд 15Свойства: количество элементов
N-1
N-2
N уровней
Сбалансированное дерево с N уровнями – это
корень и два сбалансированных поддерева; одно с N-1 уровнями, второе
– как минимум с N-2.Минимальное количество элементов такого дерева составит
k(N)=1+k(N-1)+k(N-2)
Поскольку k(1)=1, k(2)=2, получаем следующие минимальные количества:
N 3 4 5 6 7 8 9 10
k(N) 4 7 12 20 33 54 88 143
Для сравнения, минимальное число элементов полного дерева равно 2N
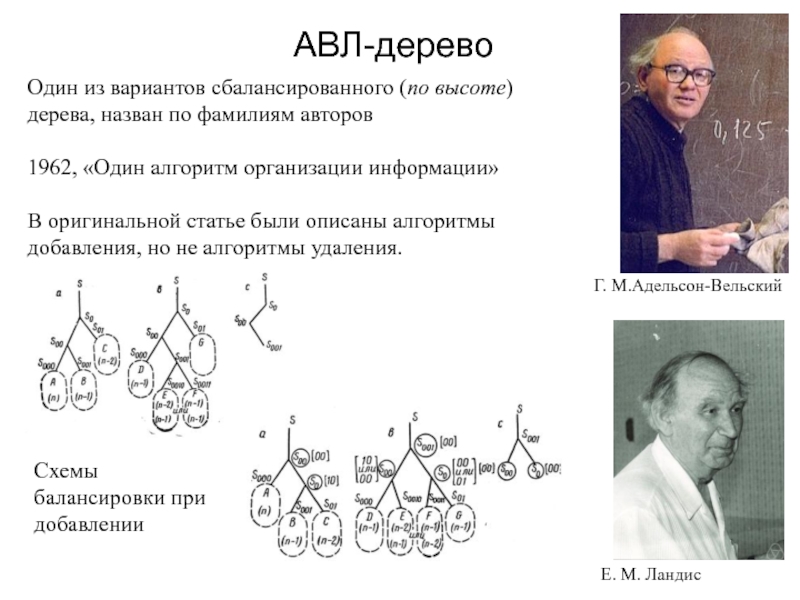
Слайд 16АВЛ-дерево
Один из вариантов сбалансированного (по высоте) дерева, назван по фамилиям
авторов
1962, «Один алгоритм организации информации»
В оригинальной статье были описаны
алгоритмы добавления, но не алгоритмы удаления.Г. М.Адельсон-Вельский
Е. М. Ландис
Схемы балансировки при добавлении
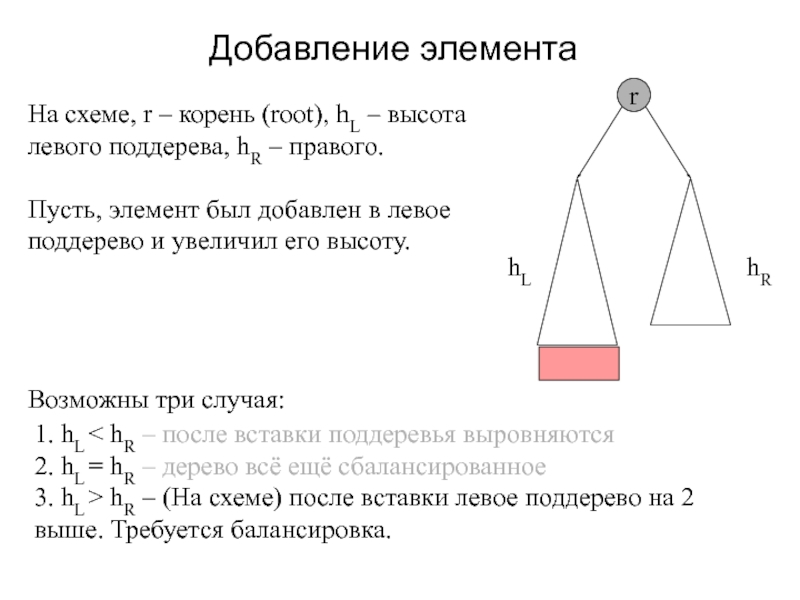
Слайд 17Добавление элемента
r
hL
hR
На схеме, r – корень (root), hL – высота
левого поддерева, hR – правого.
Пусть, элемент был добавлен в левое
поддерево и увеличил его высоту.Возможны три случая:
1. hL < hR – после вставки поддеревья выровняются
2. hL = hR – дерево всё ещё сбалансированное
3. hL > hR – (На схеме) после вставки левое поддерево на 2 выше. Требуется балансировка.
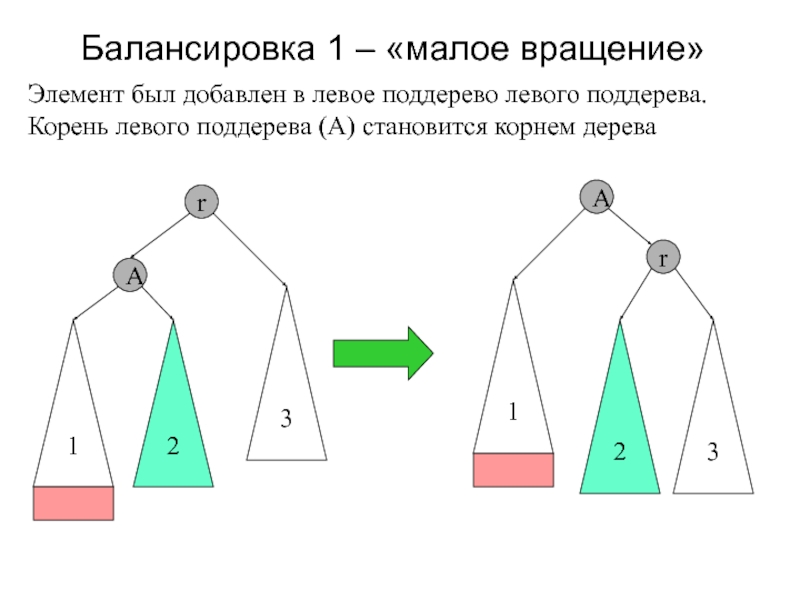
Слайд 18Балансировка 1 – «малое вращение»
r
2
3
A
1
Элемент был добавлен в левое поддерево
левого поддерева. Корень левого поддерева (A) становится корнем дерева
r
2
3
A
1
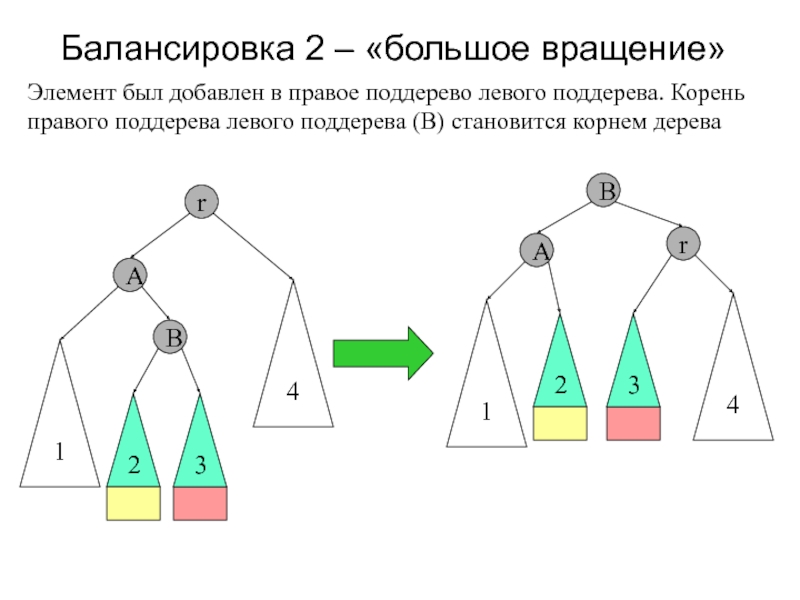
Слайд 19Балансировка 2 – «большое вращение»
r
2
4
A
1
Элемент был добавлен в правое поддерево
левого поддерева. Корень правого поддерева левого поддерева (B) становится корнем
дереваB
3
r
2
4
A
1
B
3
Слайд 22АВЛ – дерево, комментарии
Балансировка при добавлении в правое поддерево делается
симметрично.
Если расход памяти важен, для хранения состояния узла хватит 2
бит: поддеревья равны, левое выше, правое выше. Функция добавления в этом случае возвращает 1, если высота увеличилась и 0 иначе.Можно хранить высоты явно. В любом случае нет смысла использовать тип данных больше чем char для их хранения – высота всего дерева невелика даже при большом объёме данных.
Для удаления не придумано ничего лучше, чем попробовать «обратить» балансировку при добавлении. Потенциально это может привести к перестроению дерева на каждом уровне.
Слайд 23Красно-чёрное дерево
Rudolf Bayer
1972, «Symmetric Binary B-Trees. Data Structure and Maintenance
Algorithms»
Красно-чёрными деревьями эти сбалансированные деревья назвал Роберт Седжвик (Robert Sedgewick)
в 1978 году, стараясь более наглядно представить алгоритмы.В работе приведён полный набор алгоритмов – как для добавления, так и для удаления. Их много!
Первая ссылка в статье Байера – на работу Адельсона-Вельского и Ландиса
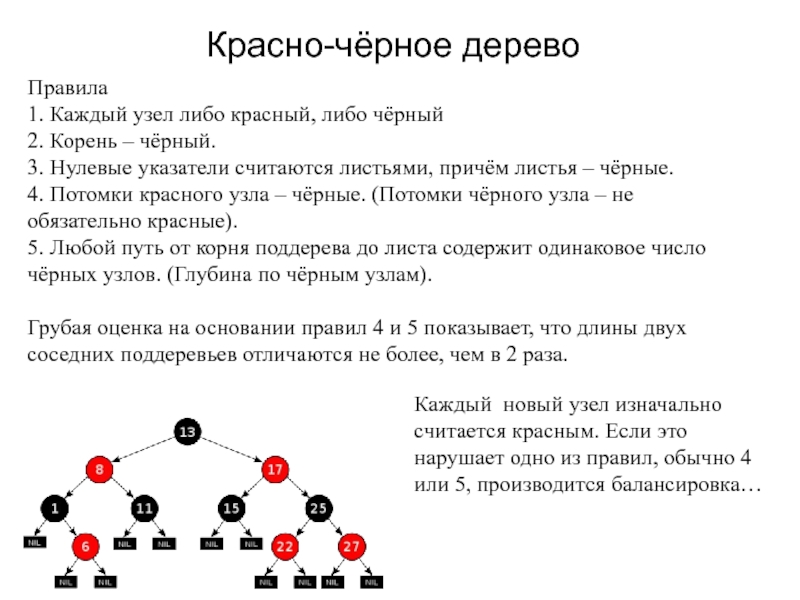
Слайд 24Красно-чёрное дерево
Правила
1. Каждый узел либо красный, либо чёрный
2. Корень –
чёрный.
3. Нулевые указатели считаются листьями, причём листья – чёрные.
4. Потомки
красного узла – чёрные. (Потомки чёрного узла – не обязательно красные).5. Любой путь от корня поддерева до листа содержит одинаковое число чёрных узлов. (Глубина по чёрным узлам).
Грубая оценка на основании правил 4 и 5 показывает, что длины двух соседних поддеревьев отличаются не более, чем в 2 раза.
Каждый новый узел изначально считается красным. Если это нарушает одно из правил, обычно 4 или 5, производится балансировка…
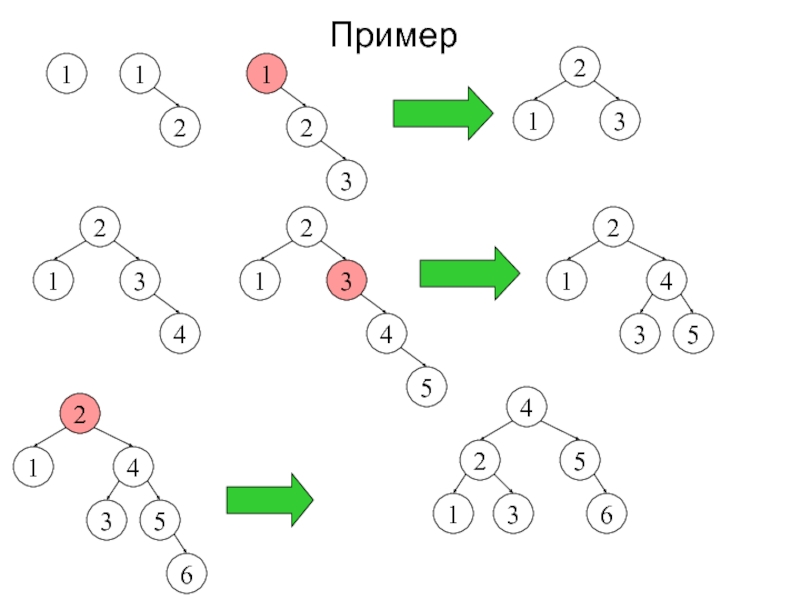
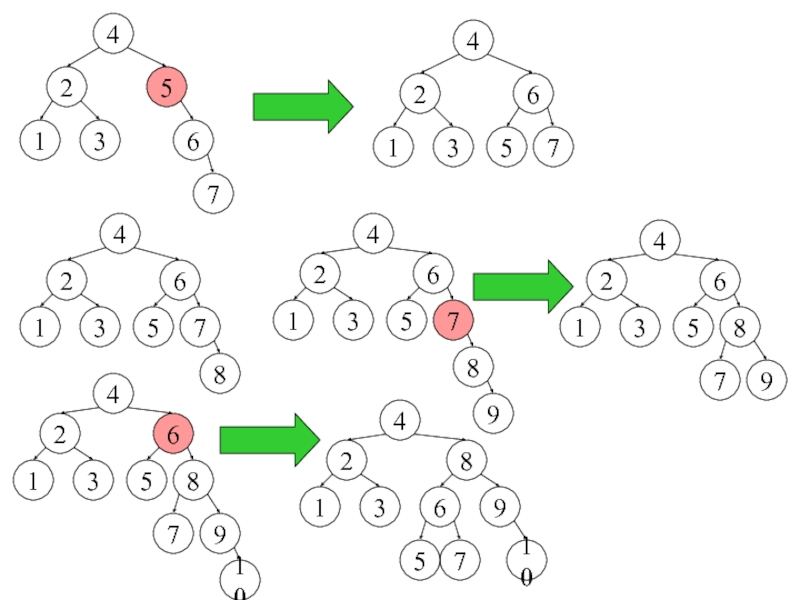
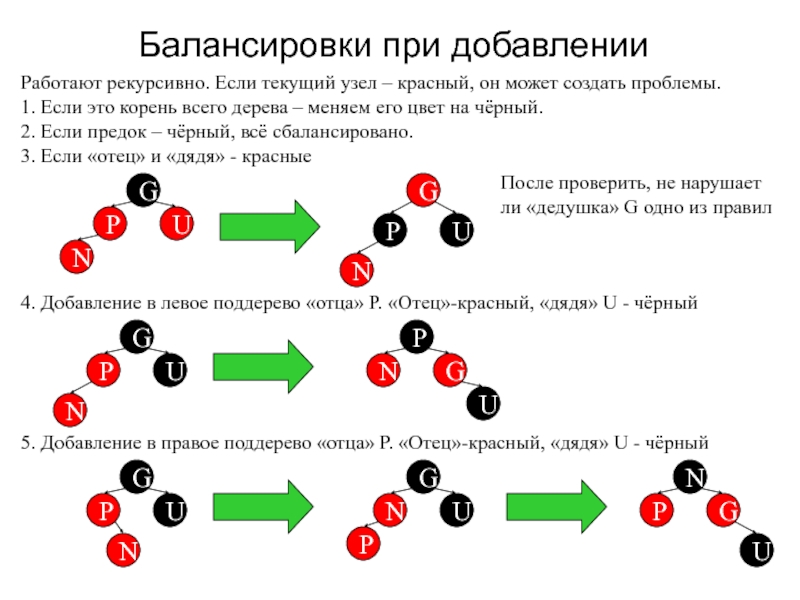
Слайд 25Балансировки при добавлении
Работают рекурсивно. Если текущий узел – красный, он
может создать проблемы.
1. Если это корень всего дерева – меняем
его цвет на чёрный.2. Если предок – чёрный, всё сбалансировано.
3. Если «отец» и «дядя» - красные
N
P
U
G
N
P
U
G
После проверить, не нарушает ли «дедушка» G одно из правил
4. Добавление в левое поддерево «отца» P. «Отец»-красный, «дядя» U - чёрный
N
P
U
G
U
N
G
P
5. Добавление в правое поддерево «отца» P. «Отец»-красный, «дядя» U - чёрный
N
P
U
G
N
P
U
G
P
U
G
N