Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция №12
Содержание
- 1. Лекция №12
- 2. Түзу не қисық сызықты жасаушылардың тұрақты түзу
- 3. Беттің параллелі деп аталатың шеңбердің жазықтығы айналу
- 4. Айналу беттеріне бізге бұрыннан таныс дөнгелек конус
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
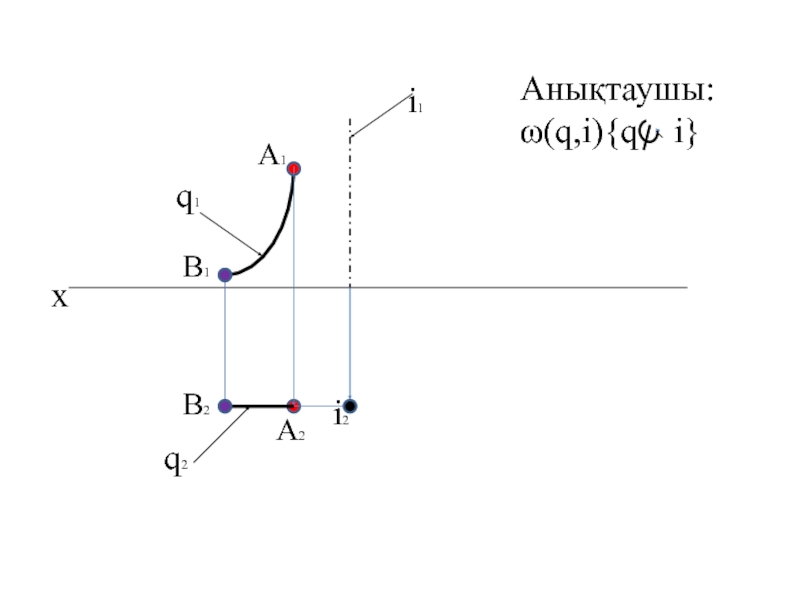
- 10. xq1q2i1i2Анықтаушы:ω(q,i){q i}A1A2B1B2
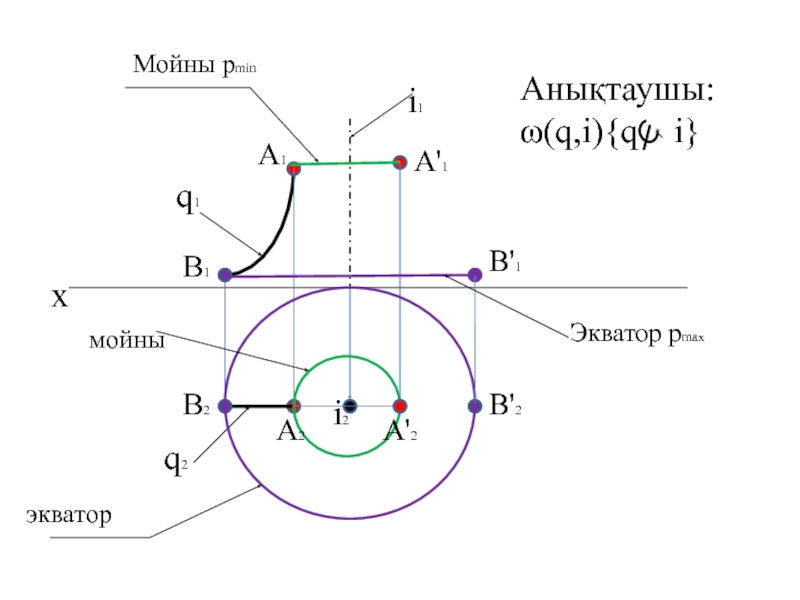
- 11. xq1q2i1i2Анықтаушы:ω(q,i){q i}A1A2A'1B1B'1A'2Мойны pminэкватормойныЭкватор pmaxB2B'2
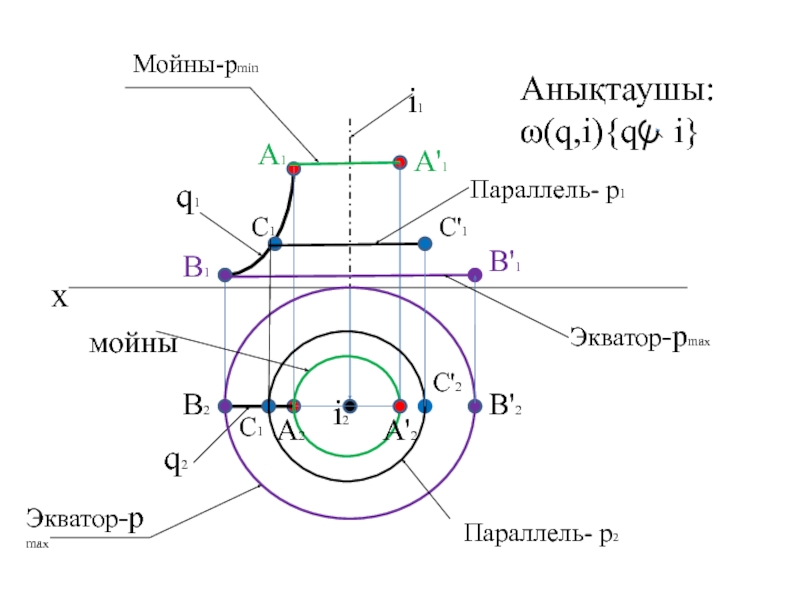
- 12. xq1q2i1i2Анықтаушы:ω(q,i){q i}A1A2A'1B1B'1A'2Мойны-pminЭкватор-pmaxмойныЭкватор-pmaxB2B'2C1C'1C1C'2Параллель- p2Параллель- p1
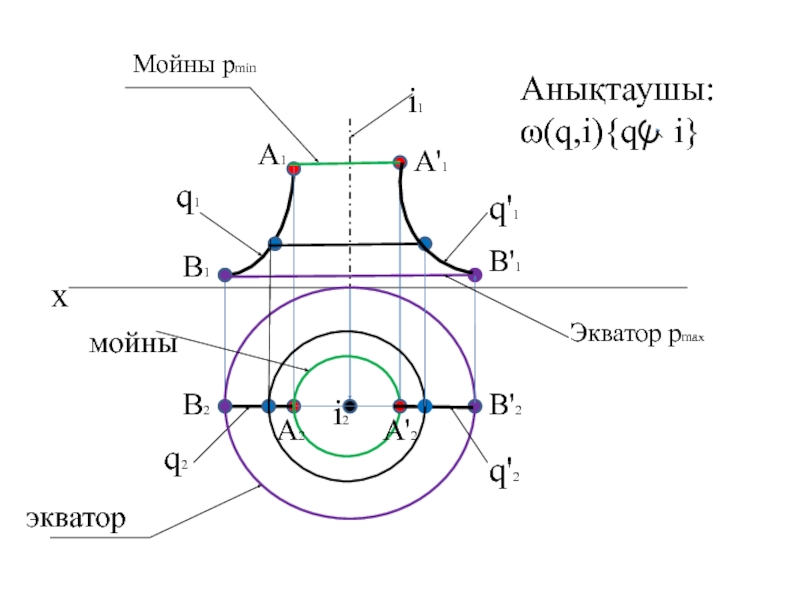
- 13. xq1q2q'2q'1i1i2Анықтаушы:ω(q,i){q i}A1A2A'1B1B'1A'2Мойны pminэкватормойныЭкватор pmaxB2B'2
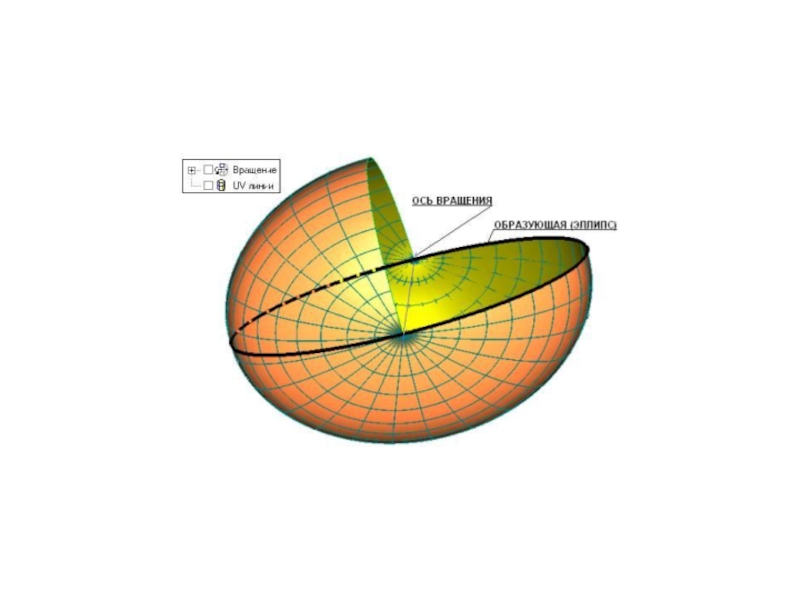
- 14. Сфера α(d, i), қайда: d- шеңбер (жасаушы),
- 15. O1O2x ЭКВАТОР; p1 maxЭКВАТОР; p2 maxБас меридиан Бас меридиан
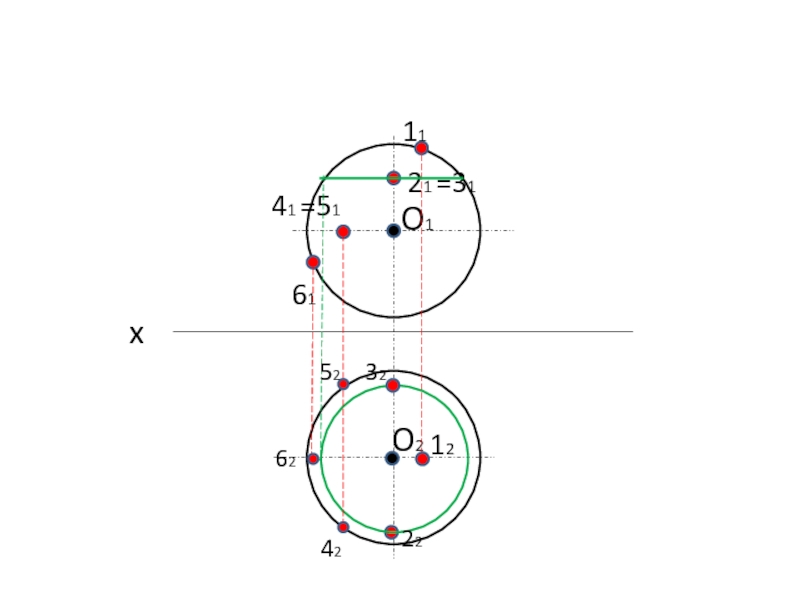
- 16. O1O2x114*1 =5161 1*2425262
- 17. O1O2x1121 =3141 =5161 123222425262
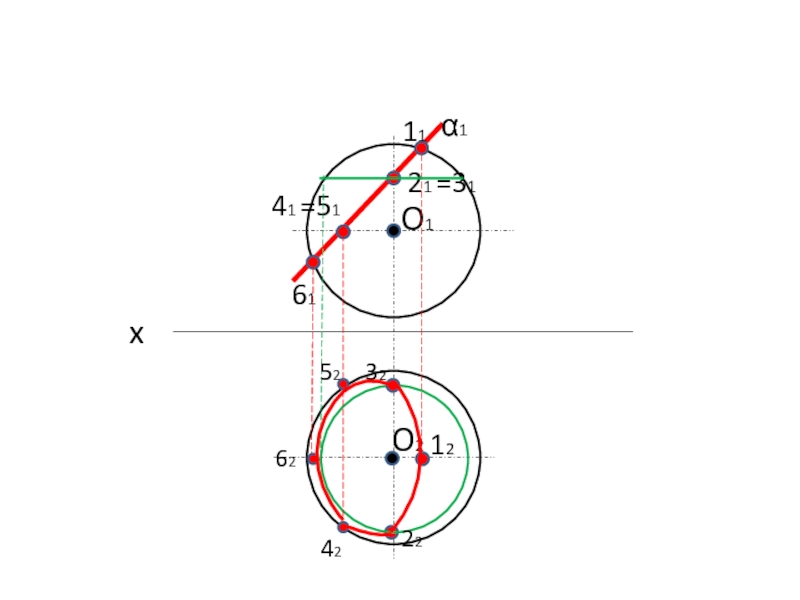
- 18. O1O2xα11121 =3141 =5161 123222425262
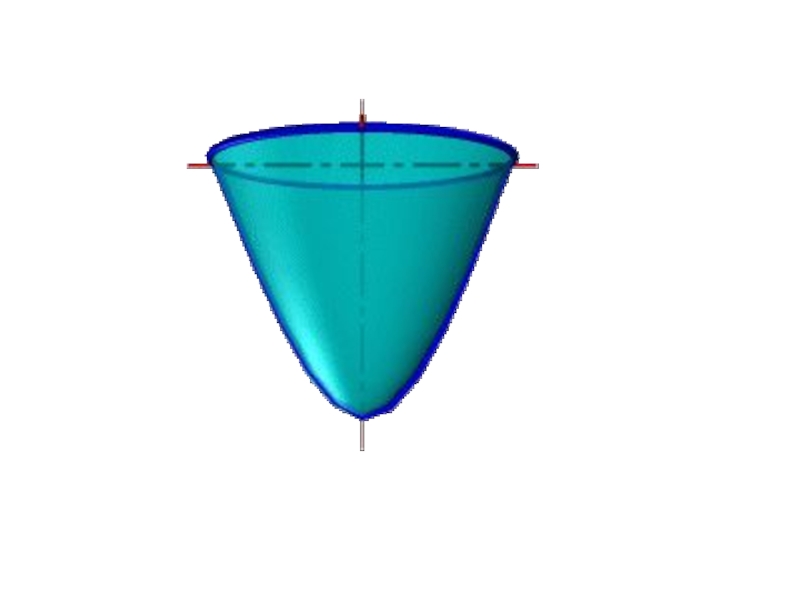
- 19. Параболоид τ (d,i), d- парабола симметрия осімен, i- айналу осі. Параболаның осі арқылы айналдырып жасалады.
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Скачать презентанцию
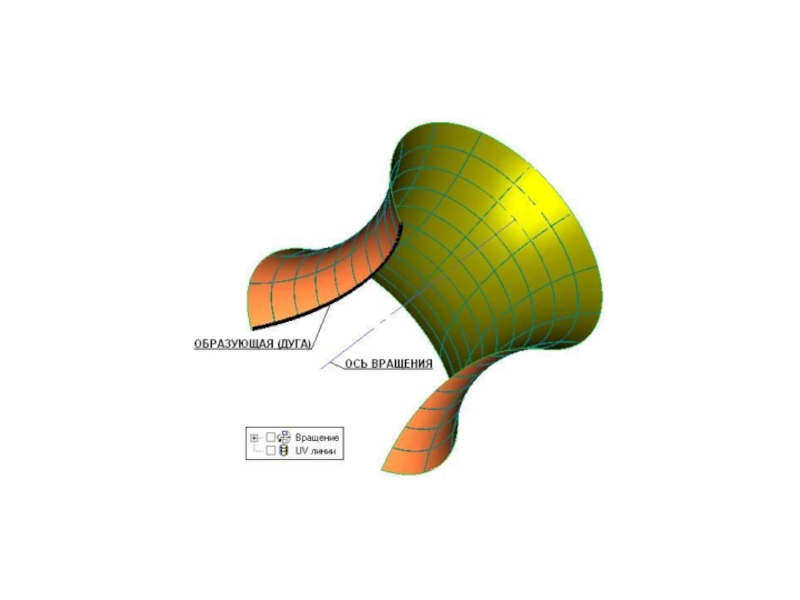
Түзу не қисық сызықты жасаушылардың тұрақты түзу төнңірегінде айналуынан жасалған беттерді айналу беттері деп атайды.Мұндай айналу беттердің проекциялар жазықтықтарының біріне перпендикуляр етіп алады.бетті жасаушының кез келген нүктесі , центрі айналу осьте
Слайды и текст этой презентации
Слайд 2Түзу не қисық сызықты жасаушылардың тұрақты түзу төнңірегінде айналуынан жасалған
беттерді айналу беттері деп атайды.
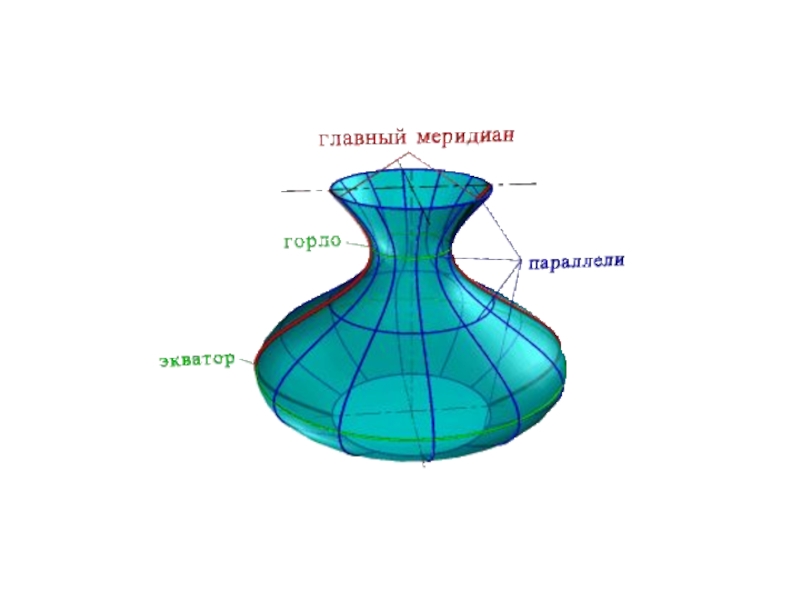
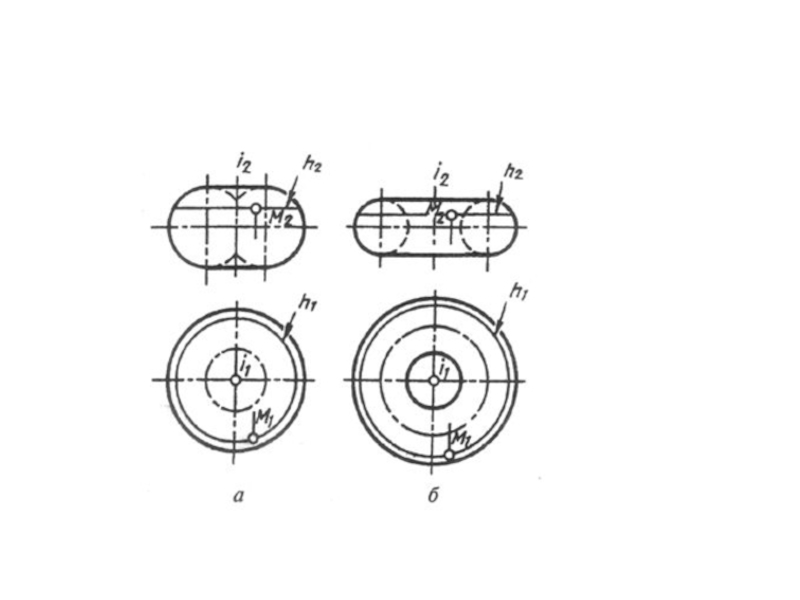
перпендикуляр етіп алады.бетті жасаушының кез келген нүктесі , центрі айналу осьте жататың шеңбер жасайды.
Слайд 3Беттің параллелі деп аталатың шеңбердің жазықтығы айналу оське перпендикуляр болады.
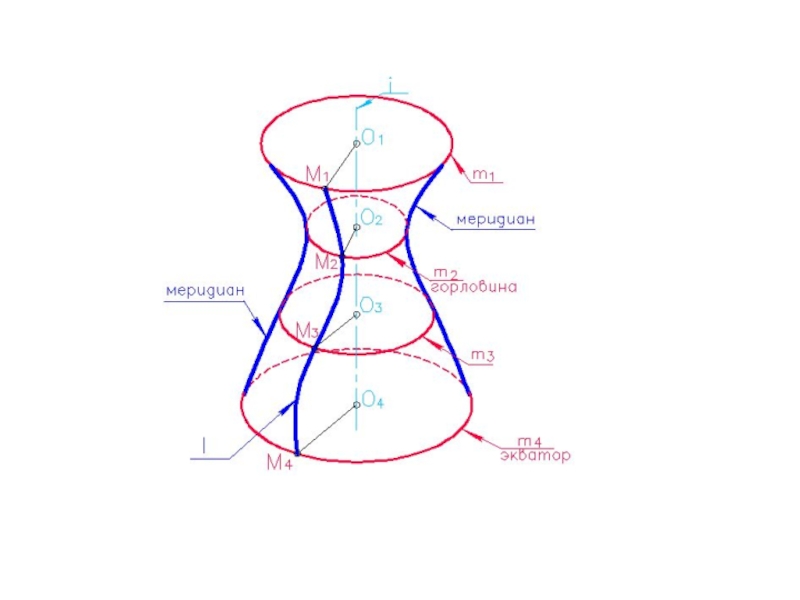
Беттің ең үлкен параллелің экватор ең кіші параллелің мойны деп
атайды.
Слайд 4Айналу беттеріне бізге бұрыннан таныс дөнгелек конус пен тік дөнгелек
цилиндр жатады.
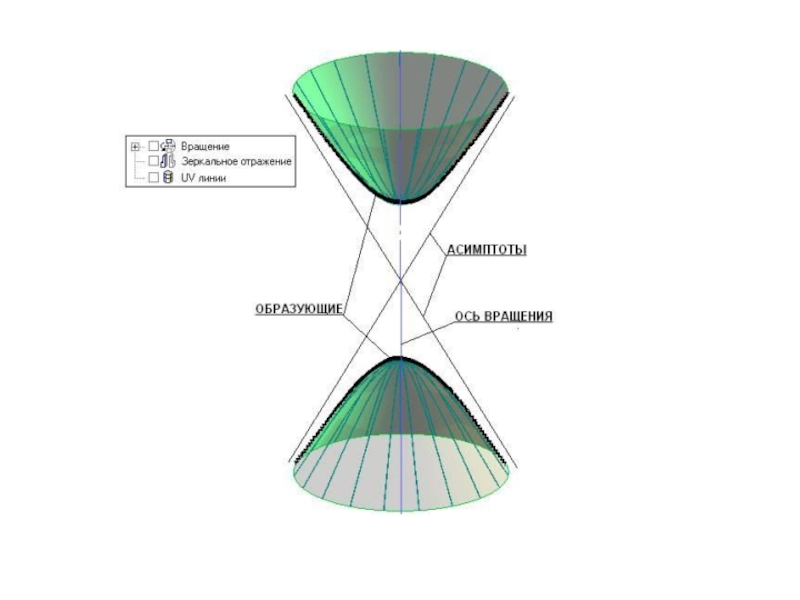
Бұлардың жасаушылары түзу сызық болып, конуста айналу осімен қіылысып
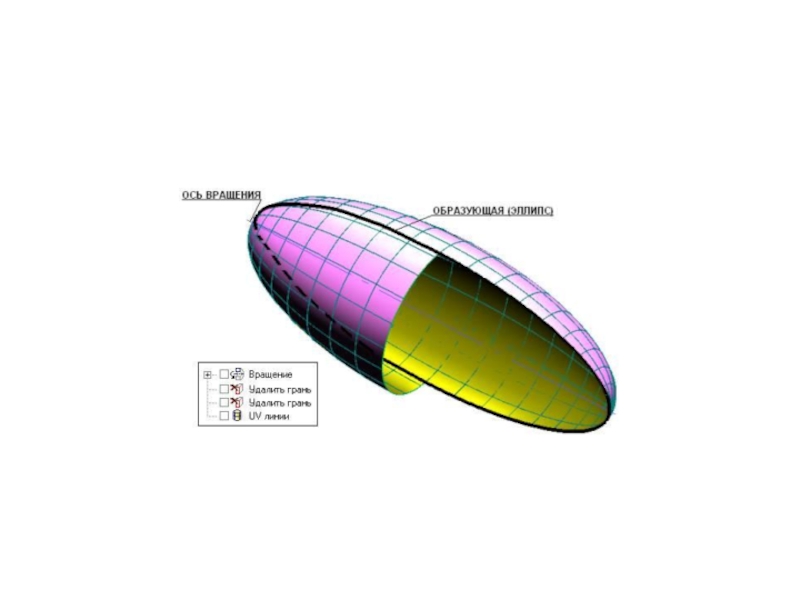
, цилиндрде параллель орналасады.Сонымен қатар жасаушылары әртүрлі қісық сызықтар болатын сфера, тор, элипсоид, параболоид және басқалары жатады.
Слайд 12x
q1
q2
i1
i2
Анықтаушы:
ω(q,i){q i}
A1
A2
A'1
B1
B'1
A'2
Мойны-pmin
Экватор-pmax
мойны
Экватор-pmax
B2
B'2
C1
C'1
C1
C'2
Параллель- p2
Параллель- p1
Слайд 14Сфера α(d, i), қайда: d- шеңбер (жасаушы), i – айналу
осі. Шеңбер өзінің диаметрі арқылы айналады.
Элипсоид ω (d,i), қайда: d
- эллипс жасаушы симметрия осімен, i -айналу осі. Эллипстің үлкен не кіші осі төңірегінде айналдыру арқылы жасалады.
Слайд 19Параболоид τ (d,i), d- парабола симметрия осімен, i- айналу осі.
Параболаның осі арқылы айналдырып жасалады.
