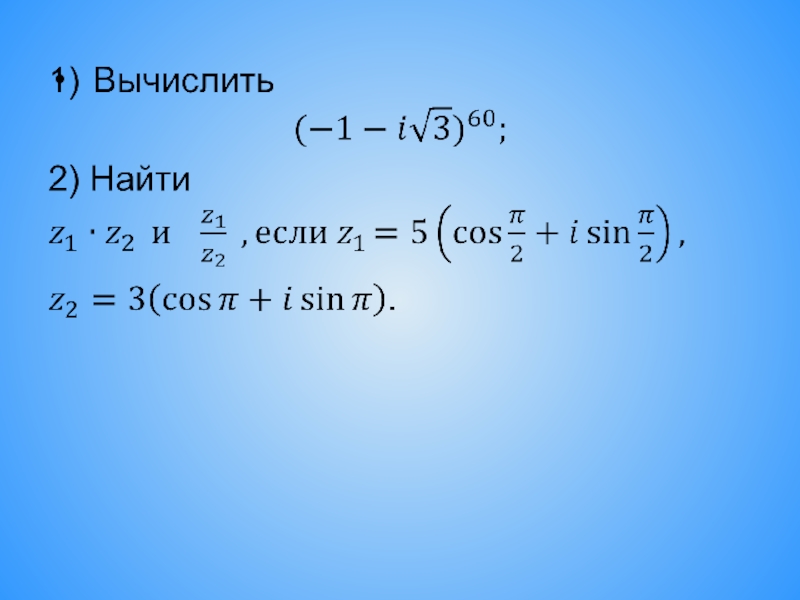Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция №1 КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Содержание
- 1. Лекция №1 КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
- 2. ПЛАН 1. Основные понятия. 2. Геометрическое изображение комплексных
- 3. 1. Основные понятия.
- 4.
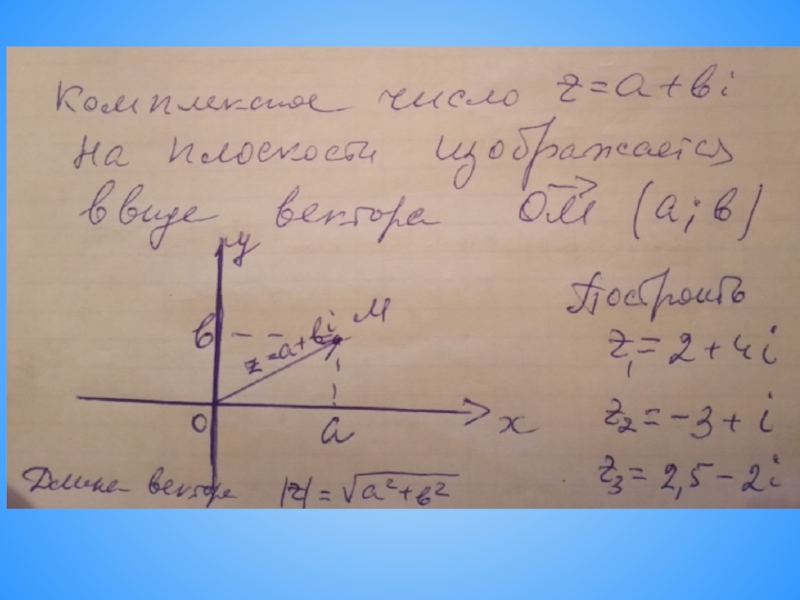
- 5. 2. Геометрическое изображение комплексных чисел. Мxy
- 6.
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. 3. Формы записи комплексных чисел.
- 12.
- 13.
- 14. 4. Действия над комплексными
- 15. Вычитание комплексныхчисел
- 16. Умножение комплексных чисел
- 17.
- 18. Деление комплексных чисел
- 19. Извлечение корней из комплексных чисел
- 20. Зачем изучать комплексные числа? На множестве С вводятся
- 21. Одним из важных приложений ТФКП является операционное
- 22.
- 23.
- 24.
- 25.
- 26. Скачать презентанцию
ПЛАН 1. Основные понятия. 2. Геометрическое изображение комплексных чисел. 3. Формы записи комплексных чисел. 4. Действия над комплексными числами. 5. Зачем изучать комплексные числа?