Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция №2 по курсу Машинная арифметика в рациональных чисел Москва, 2020
Содержание
- 1. Лекция №2 по курсу Машинная арифметика в рациональных чисел Москва, 2020
- 2. Нормализованный формат с плавающей точкой
- 3. Нормализованный формат с плавающей точкой
- 4. Нормализованный формат с плавающей точкой
- 5. Упражнение
- 6. Точность, машинное эпсилон, представление нуля
- 7. Точность, машинное эпсилон, представление нуля
- 8. Точность, машинное эпсилон, представление нуля
- 9. Представление нуля2 способа представления нуля:в мантиссеспециальная строка в поле экспоненты
- 10. Стандарт формата с плавающей точкой
- 11. Смещенная экспонентаСубнормальные числа - поле экспоненты имеет
- 12. Стандарт формата с плавающей точкой IEEE 754-1985
- 13. Специальные числа формата с плавающей точкой В
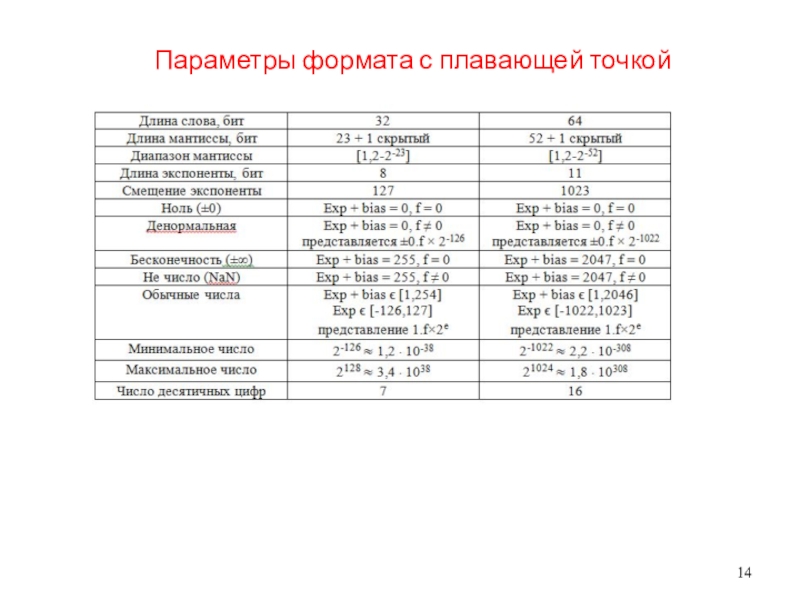
- 14. Параметры формата с плавающей точкой
- 15. Денормализованные числа с плавающей точкойДенормализованные числа -
- 16. Распределение чисел с плавающей точкой с учётом
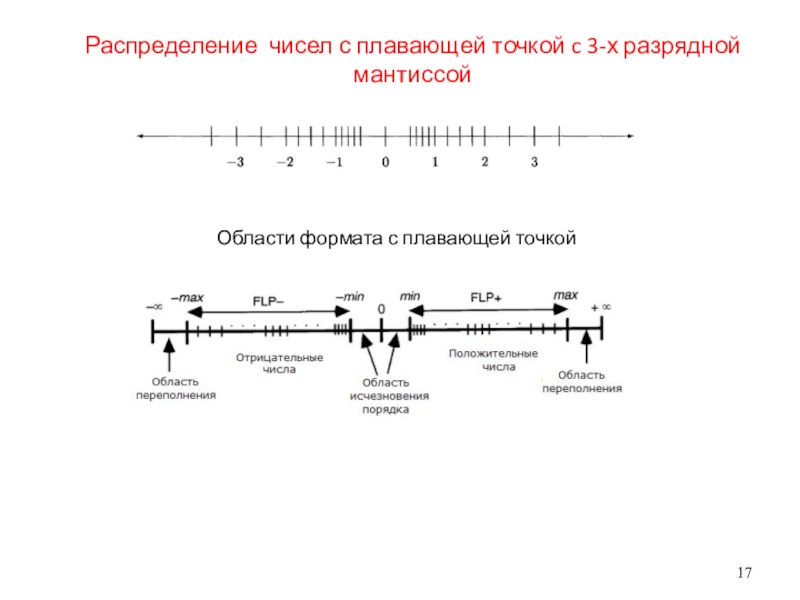
- 17. Распределение чисел с плавающей точкой c 3-х разрядной мантиссойОбласти формата с плавающей точкой
- 18. Округление чисел с плавающей точкой
- 19. Округление чисел с плавающей точкой
- 20. Округление чисел с плавающей точкой
- 21. Округление чисел с плавающей точкой
- 22. Округление чисел с плавающей точкойУпражнение 1. Каковы бинарные
- 23. ОШИБКИ ПРИ КОМПЬЮТЕРНЫХ ВЫЧИСЛЕНИЯХ
- 24. ОШИБКИ ПРИ КОМПЬЮТЕРНЫХ ВЫЧИСЛЕНИЯХ
- 25. ОШИБКИ ПРИ КОМПЬЮТЕРНЫХ ВЫЧИСЛЕНИЯХ
- 26. Основные алгоритмы арифметики с плавающей точкой
- 27. Основные алгоритмы арифметики с плавающей точкой
- 28. Основные алгоритмы арифметики с плавающей точкой
- 29. Основные алгоритмы арифметики с плавающей точкой
- 30. Сложение чисел с плавающей точкой
- 31. Сложение чисел с плавающей точкой
- 32. Скачать презентанцию
Нормализованный формат с плавающей точкой
Слайды и текст этой презентации
Слайд 9Представление нуля
2 способа представления нуля:
в мантиссе
специальная строка в поле экспоненты
Слайд 11Смещенная экспонента
Субнормальные числа - поле экспоненты имеет нулевые биты, а
поле мантиссы содержит ненулевые биты.
1 до 254, представляющие фактические показатели от -126 до 127.Слайд 12Стандарт формата с плавающей точкой IEEE 754-1985
Формат с плавающей
точкой одинарной точности имеет длину 32 бита, тогда как для
двойной точности требуется 64 бит. Эти два формата имеют 8- и 11-битные поля экспоненты и используют экспоненциальные смещения 127 и 1023 соответственно.Мантисса находится в диапазоне [1, 2], с ее единственным целым битом, который всегда равен 1 и удаляется и отображается только дробная часть. Обозначения «23 + 1» или «52 + 1» для длины мантиссы объясняют роли скрытого бита, что вносит свой вклад в точность, не занимая места.
Слайд 13Специальные числа формата с плавающей точкой
В стандартном формате IEEE
существует две бесконечности ( -∞, +∞), естественно иметь два представления
нуля (+0 = 1/+∞, -0 = 1/-∞) в соответствием со стандартом IEEE 754. Специальные коды NaN (не-число) также необходимы для представления неопределенных результатов, таких как, например, 0/0, (+∞) – (-∞), корень квадратный из минус единицы и др. Cпециальные коды позволяют исключать распространение исключений в процессе вычислений и останавливать ход работы программы. Некоторые реализации формата с плавающей точкой отличаются между собой различными видами NaN.Обычное число ÷ (+∞) = ± 0,
(+∞) × Обычное число = ± ∞,
NaN + Обычное число = NaN.
Слайд 15Денормализованные числа с плавающей точкой
Денормализованные числа - это вид чисел
с плавающей запятой, определённый в стандарте IEEE 754. Мантисса этих
чисел начинается с 0, а не с 1 (нет неявной единицы), а порядок — минимально возможный.Необходимы, чтобы сделать эффект исчезновения порядка менее резким
Слайд 16Распределение чисел с плавающей точкой с учётом денормализованных чисел
Упражнение .
Какова
разница между 2 и первым числом в формате IEEE большим,
чем 2? Какова разница между 1024 и первым числом в формате IEEE большим, чем 1024?Слайд 17Распределение чисел с плавающей точкой c 3-х разрядной мантиссой
Области формата
с плавающей точкой
Слайд 22Округление чисел с плавающей точкой
Упражнение 1.
Каковы бинарные представления IEEE в
формате с плавающей точкой одинарной точности для округленного значения …
, используя каждый из четырех режимов округления?Упражнение 2.
Какое наибольшее число с плавающей запятой x, для которого 1 + x - это точно 1, при условии, что формат одинарной точности, а режим округления до ближайшего? Что если формат IEEE двойной точности?