Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция №5 Солодухин Е.А
Содержание
- 1. Лекция №5 Солодухин Е.А
- 2. Способы преобразования проекций
- 3. Способы преобразования проекций применяют для получения нового
- 4. Слайд 4
- 5. Дополнительное проецирование
- 6. При дополнительном методе проецирования объект в пространстве
- 7. В качестве плоскости проекций при дополнительном проецировании
- 8. Дополнительное проецирование на основе центрального проецирования
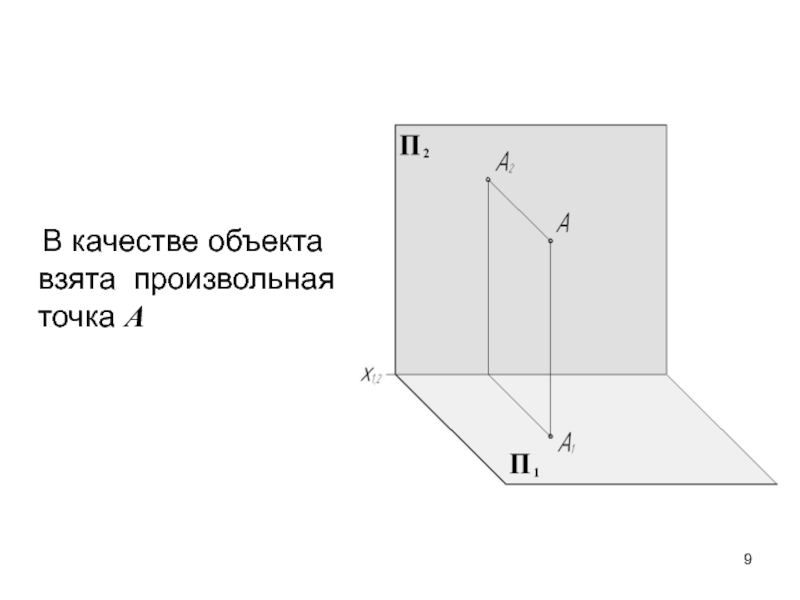
- 9. В качестве объекта взята произвольная точка А
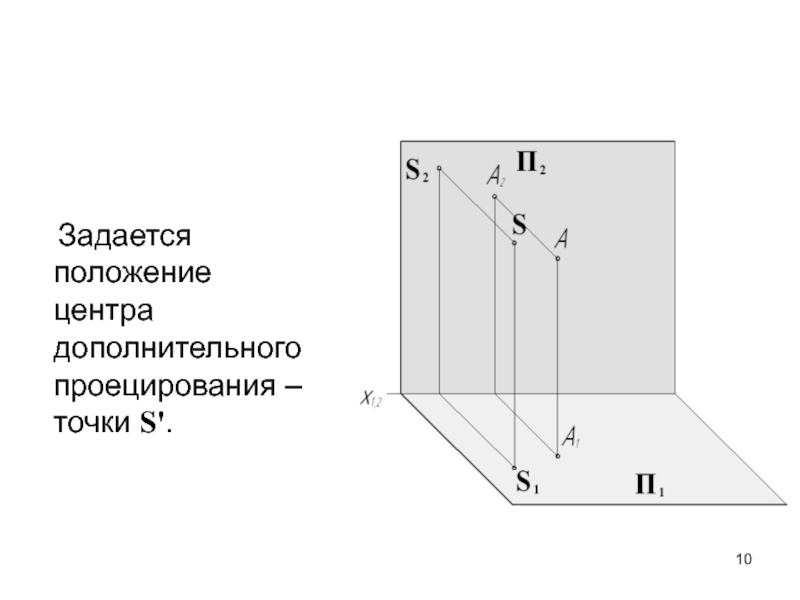
- 10. Задается положение центра дополнительного проецирования – точки S'.
- 11. Выбирается дополнительная плоскость проекций
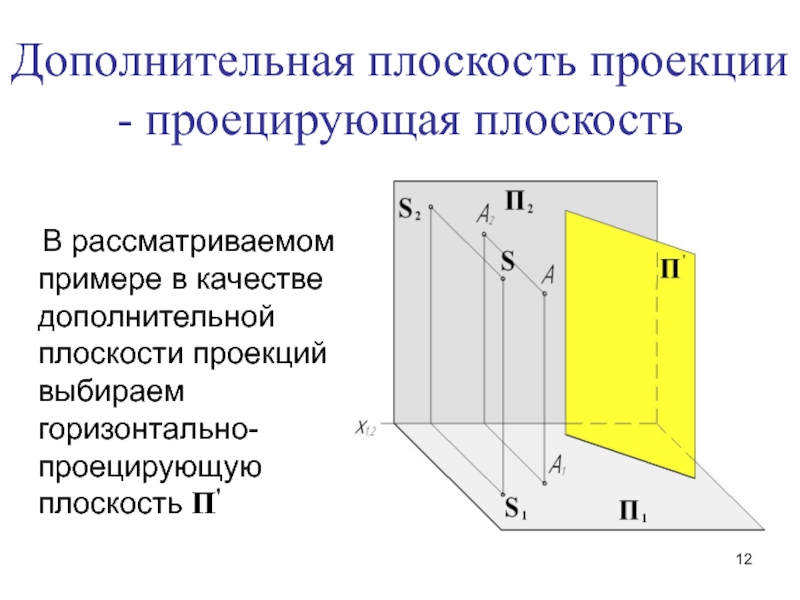
- 12. В рассматриваемом примере в качестве
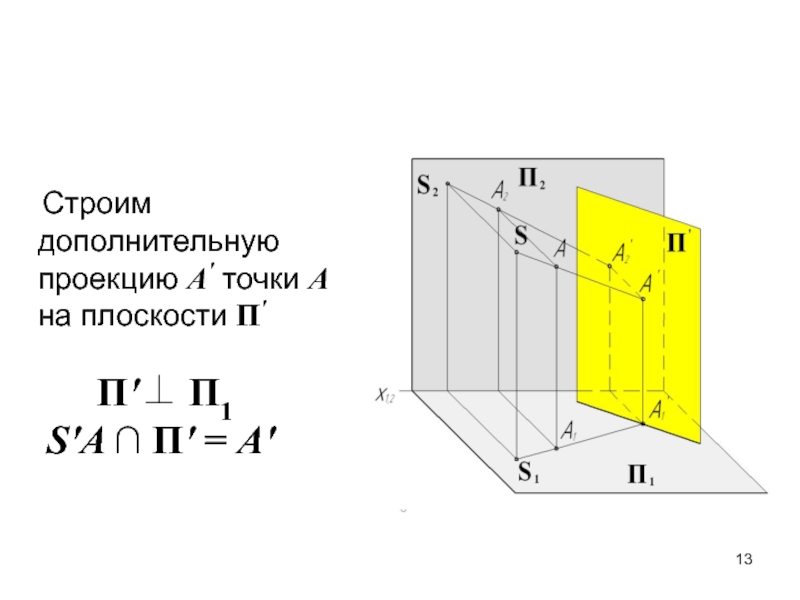
- 13. Строим дополнительную проекцию А' точки
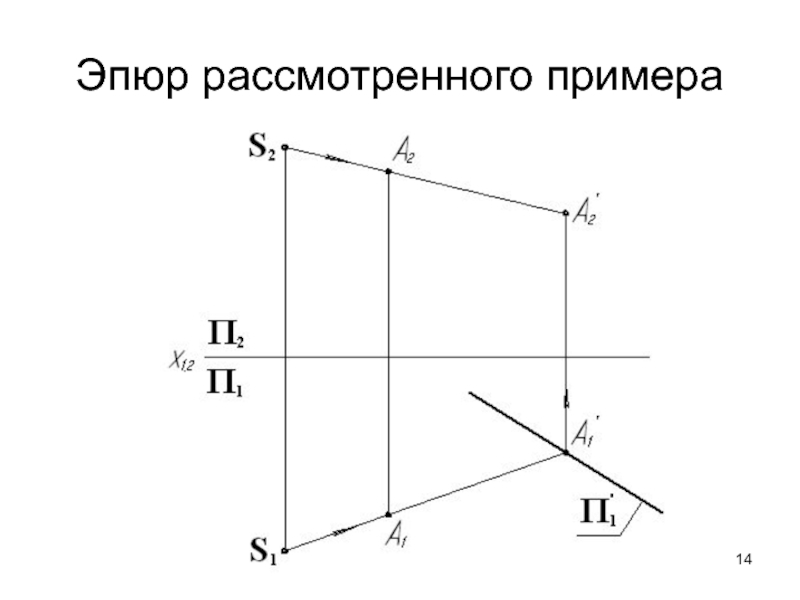
- 14. Эпюр рассмотренного примера
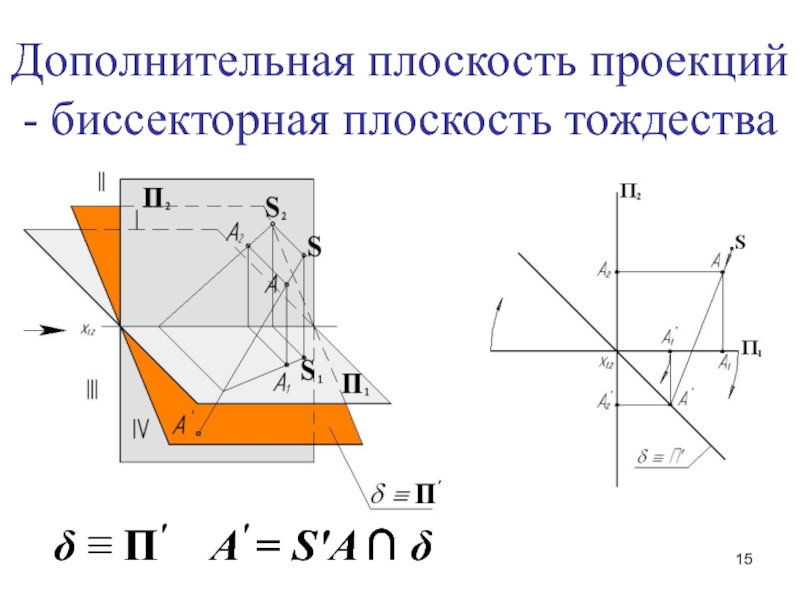
- 15. δ ≡ П' A' = S'A ∩ δДополнительная плоскость проекций - биссекторная плоскость тождества
- 16. ЭпюрП‘ – биссекторная плоскость тождества. Следовательно, если
- 17. В рассматриваемом примере в качестве
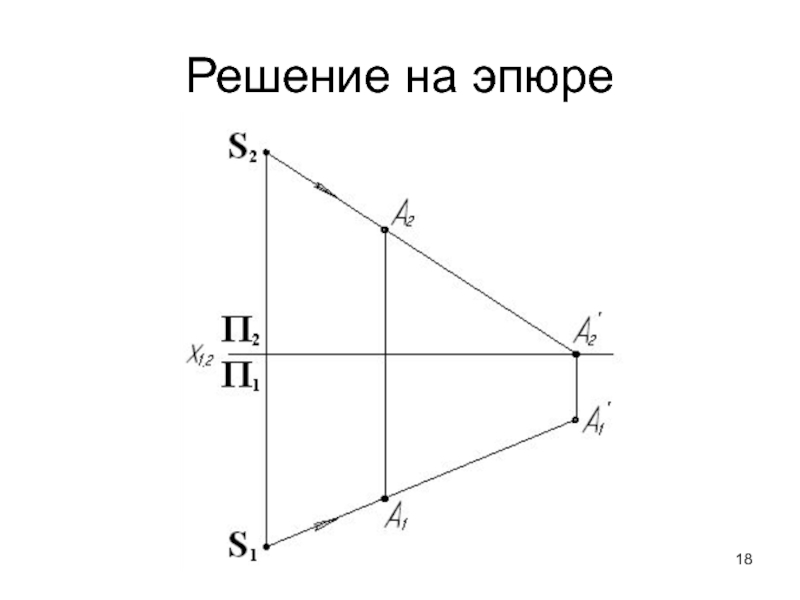
- 18. Решение на эпюре
- 19. Дополнительное проецирование на основе параллельного косоугольного проецирования
- 20. Отличие данного варианта дополнительного проецирования от рассмотренного
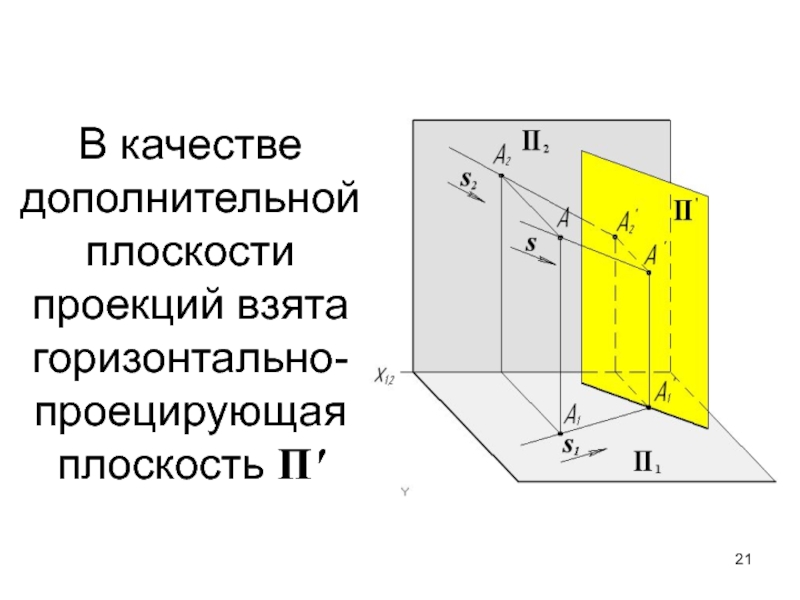
- 21. В качестве дополнительной плоскости проекций взята горизонтально-проецирующая плоскость П'
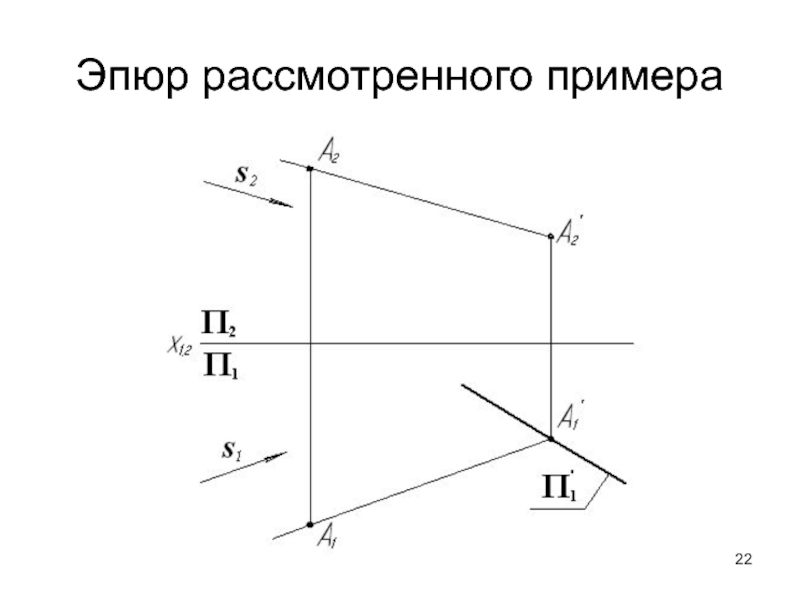
- 22. Эпюр рассмотренного примера
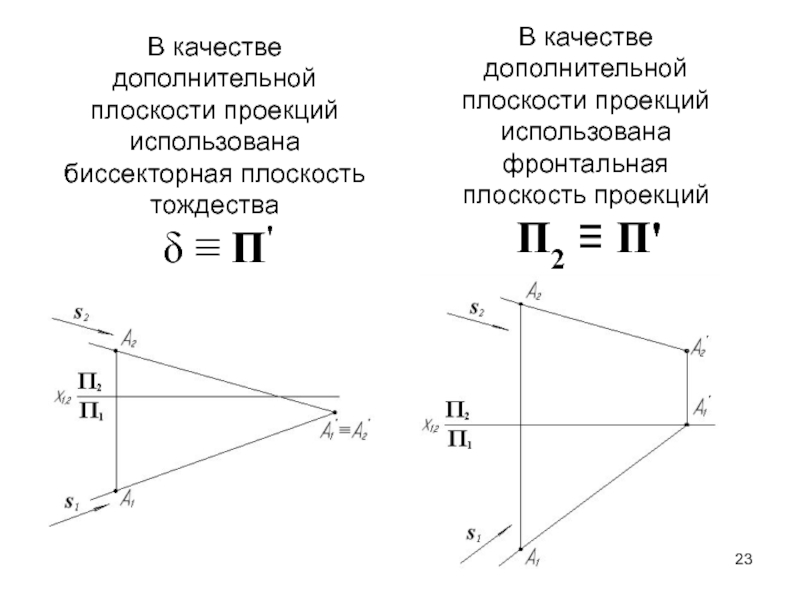
- 23. В качестве дополнительной плоскости проекций использована биссекторная
- 24. Перемена плоскостей проекций - дополнительное прямоугольное проецирование
- 25. Подбираемая дополнительная плоскость проекций должна быть только
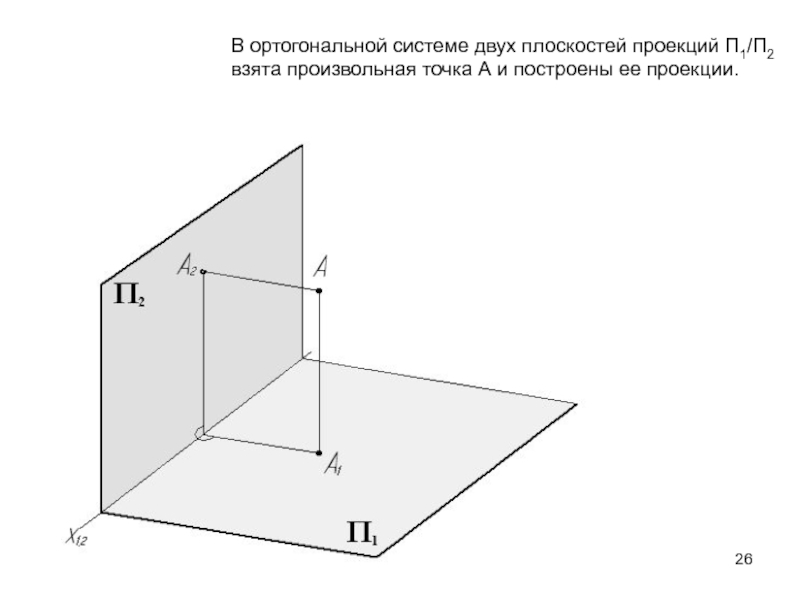
- 26. В ортогональной системе двух плоскостей проекций П1/П2взята произвольная точка А и построены ее проекции.
- 27. Вводится дополнительная плоскость проекций П4. Например, горизонтально-проецирующая.Таким
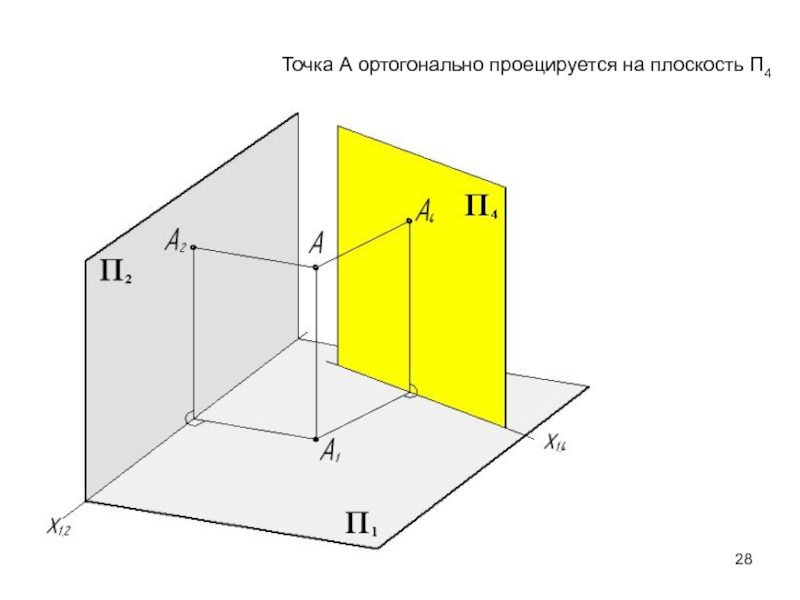
- 28. Точка А ортогонально проецируется на плоскость П4
- 29. Принцип построения эпюраТак как точка А не
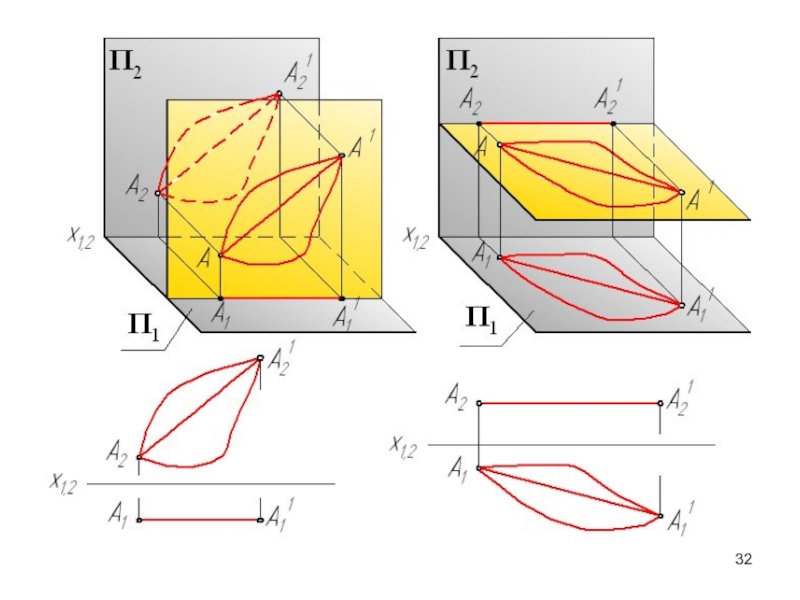
- 30. Плоскопараллельное перемещение
- 31. При плоскопараллельном перемещении все точки заданного объекта
- 32. Слайд 32
- 33. При плоскопараллельном перемещении угол наклона объекта к
- 34. Вращение
- 35. Каждая точка объекта вращается вокруг выбранной оси,
- 36. Ось вращения – проецирующая прямаяПлоскость вращения
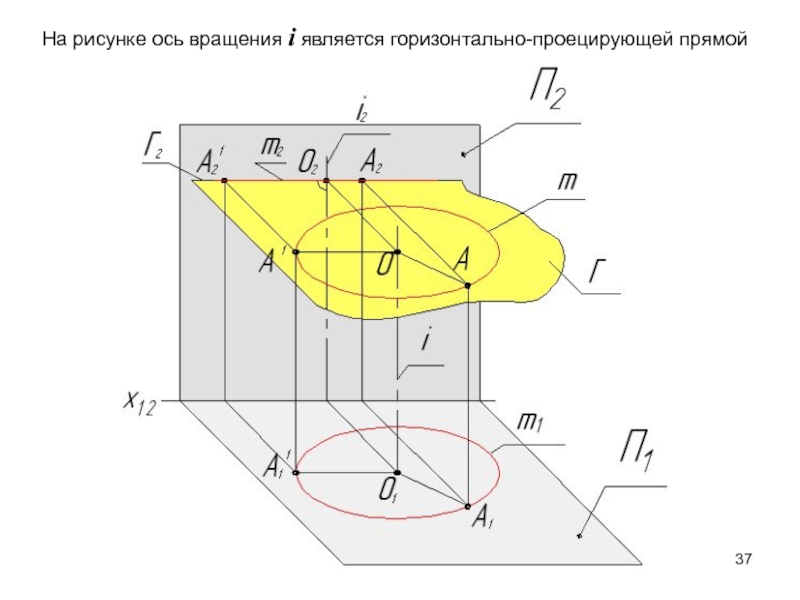
- 37. На рисунке ось вращения i является горизонтально-проецирующей прямой
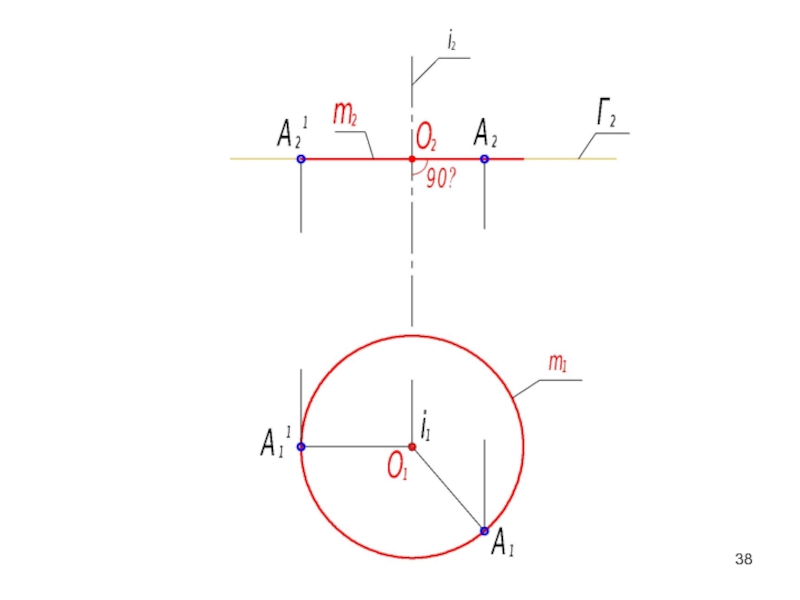
- 38. Слайд 38
- 39. Ось вращения – прямая уровня
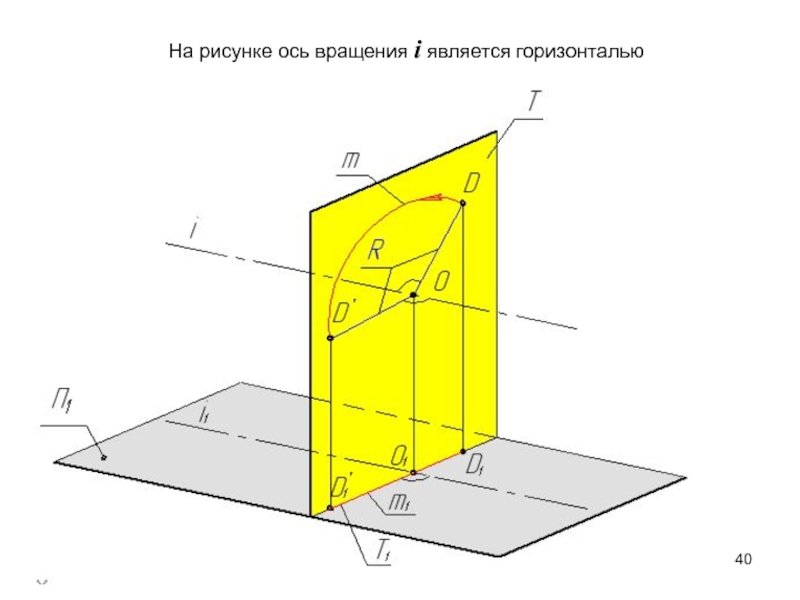
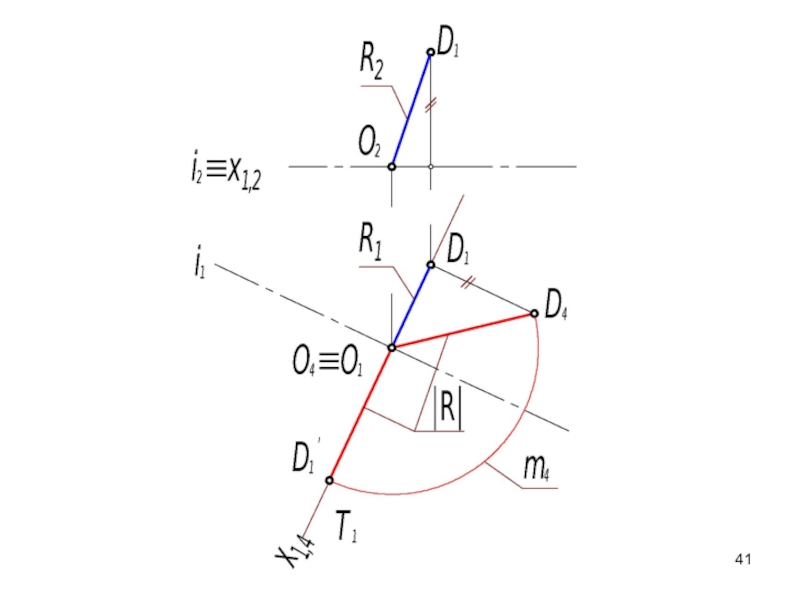
- 40. На рисунке ось вращения i является горизонталью
- 41. Слайд 41
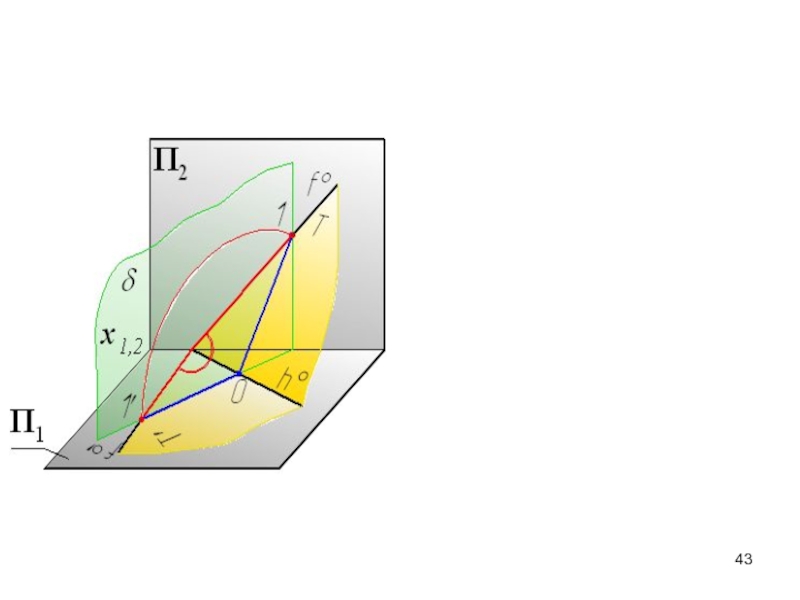
- 42. Совмещение с плоскостью проекций (вращение плоской фигуры
- 43. Слайд 43
- 44. Скачать презентанцию
Способы преобразования проекций
Слайды и текст этой презентации
Слайд 6При дополнительном методе проецирования объект в пространстве не перемещается.
На базе
исходных ортогональных проекций на одной из основных плоскостей проекций П1
или П2 либо на дополнительной плоскости проекций П' строится новая дополнительная проекция заданного объекта или группы объектов на основе другого варианта метода проецирования.
Слайд 7В качестве плоскости проекций при дополнительном проецировании наиболее часто используют:
для центрального и параллельного
косоугольного
вариантов метода проецирования:- дополнительную проецирующую
плоскость;
- биссекторную плоскость тождества;
- одну из основных плоскостей проекций.
для перемены плоскостей проекций
(дополнительного прямоугольного проецирования):
- только дополнительную проецирующую
плоскость.
Слайд 12 В рассматриваемом примере в качестве дополнительной плоскости проекций
выбираем горизонтально-проецирующую плоскость П'
Дополнительная плоскость проекции - проецирующая плоскость
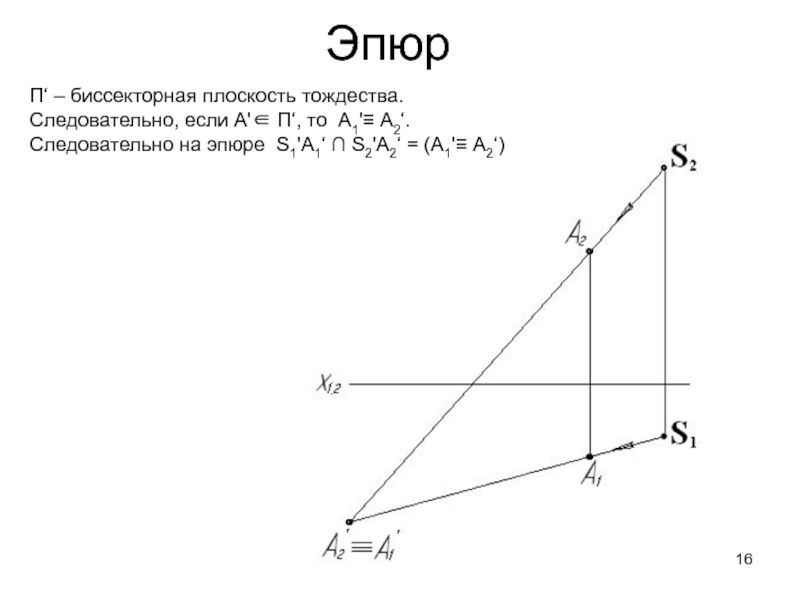
Слайд 16Эпюр
П‘ – биссекторная плоскость тождества.
Следовательно, если А' ‘, то
А1' А2‘.
Следовательно на эпюре S1'А1‘ ∩ S2'А2‘ = (А1' А2‘)
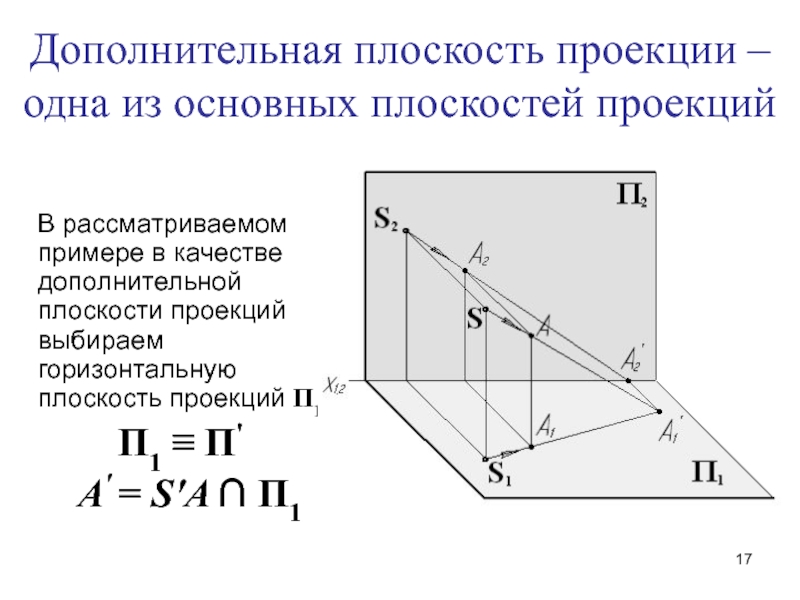
Слайд 17 В рассматриваемом примере в качестве дополнительной плоскости проекций
выбираем горизонтальную плоскость проекций П1
П1 ≡ П'A' = S'A ∩ П1
Дополнительная плоскость проекции – одна из основных плоскостей проекций
Слайд 20Отличие данного варианта дополнительного проецирования от рассмотренного ранее состоит только
в замене центра проецирования S' на направление проецирования в виде
вектора s.
Слайд 23В качестве дополнительной плоскости проекций использована биссекторная плоскость тождества δ
≡ П'
В качестве
дополнительной
плоскости проекций
использована
фронтальная
плоскость проекций
П2 ≡ П'
Слайд 25Подбираемая дополнительная плоскость проекций должна быть только проецирующей. Тем самым
создаётся новая прямоугольная система плоскостей проекций.
Подбираемые дополнительные плоскости проекций обозначаются
П4, П5, П6 и т.д.
Слайд 26В ортогональной системе двух плоскостей проекций П1/П2
взята произвольная точка А
и построены ее проекции.
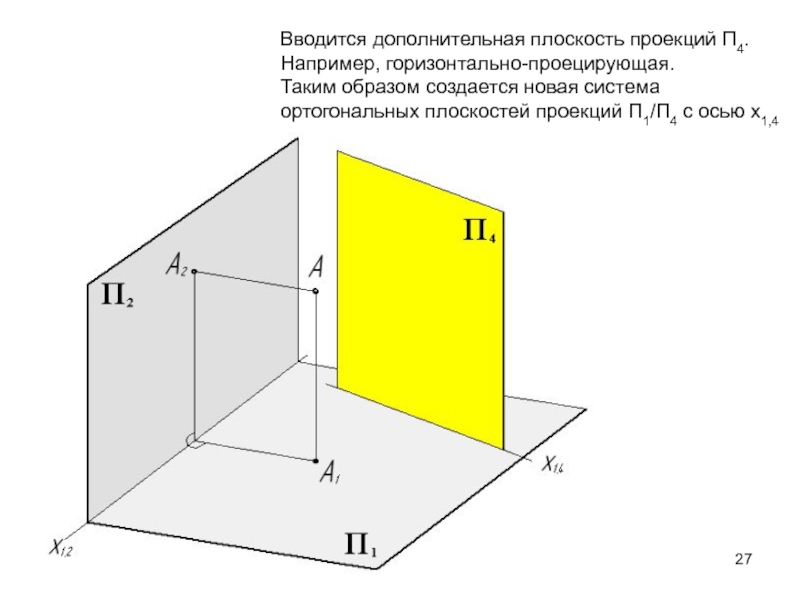
Слайд 27Вводится дополнительная плоскость проекций П4.
Например, горизонтально-проецирующая.
Таким образом создается новая
система
ортогональных плоскостей проекций П1/П4 с осью х1,4
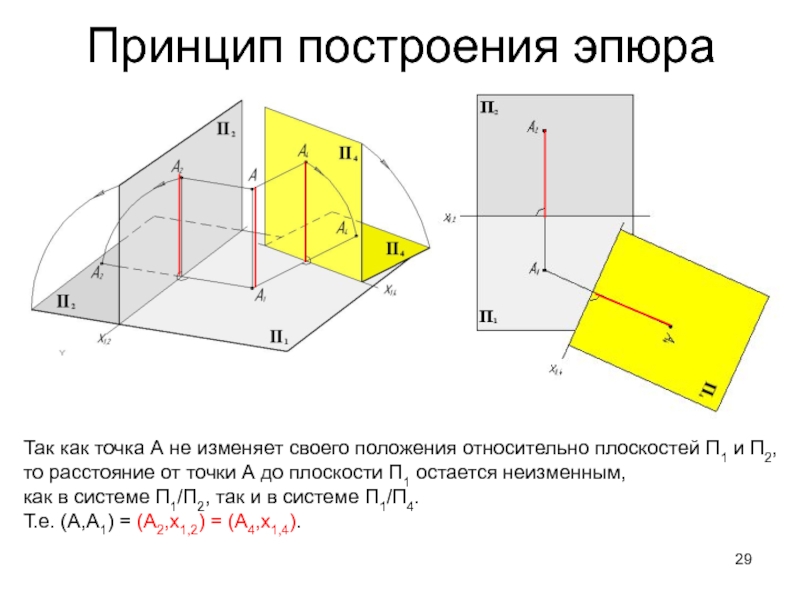
Слайд 29Принцип построения эпюра
Так как точка А не изменяет своего положения
относительно плоскостей П1 и П2,
то расстояние от точки А до
плоскости П1 остается неизменным, как в системе П1/П2, так и в системе П1/П4.
Т.е. (А,А1) = (А2,х1,2) = (А4,х1,4).
Слайд 31При плоскопараллельном перемещении все точки заданного объекта свободно перемещаются в
плоскостях параллельных какой-либо одной из основных плоскостей проекций П1 или
П2.Так как линии перемещения точек имеют произвольную форму, их проекции никогда не показываются, в отличие от способа вращения.
Интересует только конечный результат, а не процесс перемещения.
На другой плоскости проекций перемещение каждой точки объекта выражается в виде прямой линии, параллельной оси х1,2.
Слайд 33При плоскопараллельном перемещении угол наклона объекта к той плоскости проекций,
параллельно которой осуществляется перемещение, не изменяется.
Следовательно, проекция объекта на
эту плоскость до и после перемещения не изменяет своей формы и величины – они конгруэнтны.
Слайд 35Каждая точка объекта вращается вокруг выбранной оси, перемещаясь по окружности,
лежащей в плоскости перпендикулярной оси вращения.
Линии перемещения обязательно показываются.
Осью
вращения может быть только прямая частного положения – прямая уровня или проецирующая прямая.
Слайд 36Ось вращения –
проецирующая прямая
Плоскость вращения точки является плоскостью уровня.
Траектория
перемещения точки - окружность отображается в виде окружности на той
плоскости проекций, перпендикулярно которой расположена ось вращения.На другой плоскости проекций траектория перемещения точки отображается в виде прямой линии, перпендикулярной проекции оси вращения (параллельной оси х1,2).
При вращении вокруг проецирующей прямой, угол наклона объекта к той плоскости проекций, перпендикулярно которой расположена ось вращения, не изменяется.
Следовательно, проекция объекта на эту плоскость до и после перемещения не изменяет своей формы и величины – они конгруэнтны.
Слайд 39Ось вращения –
прямая уровня
Плоскость вращения точки -
проецирующую плоскость.
На плоскости проекций, параллельно которой расположена ось
вращения, траектория перемещения точки имеет форму прямой, а на другой – форму эллипса, что не дает возможности ее использования. Все построения выполняются только на одной проекции.
Вся задача сводится к определению истинной величины радиуса вращения точки.
Данный способ вращения имеет следующие ограничения:
- применим практически только к плоским фигурам;
- ось вращения должна лежать в плоскости поворачивае-
мой фигуры.
Слайд 42Совмещение с плоскостью проекций (вращение плоской фигуры вокруг линии пересечения плоскости,
в которой лежит заданная фигура, с плоскостью проекций)
