Лекция9

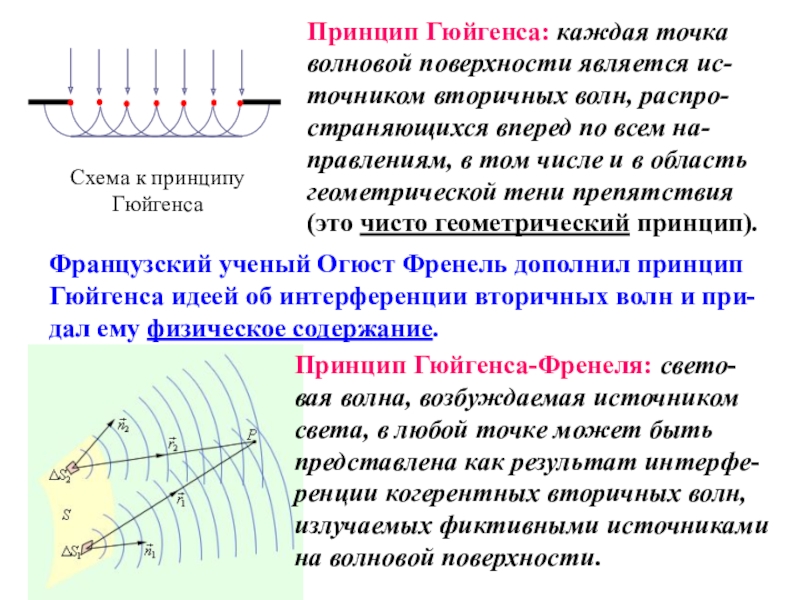
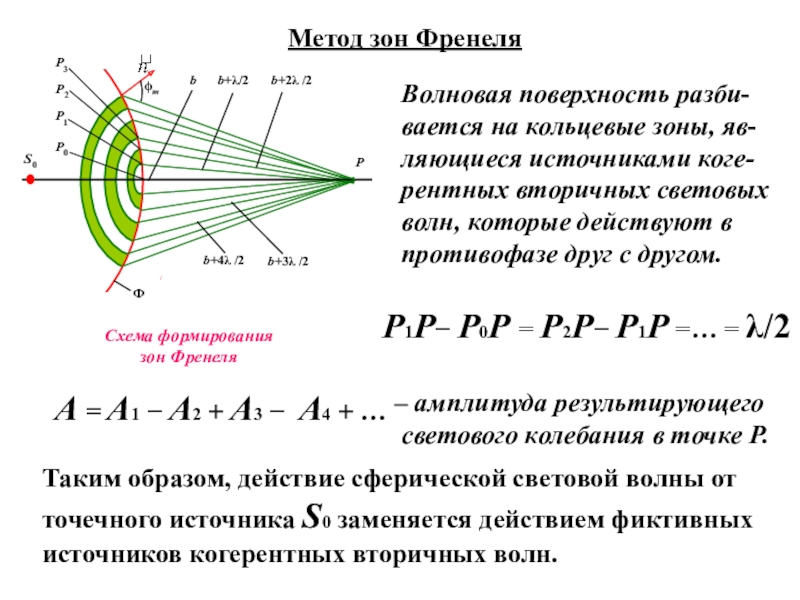
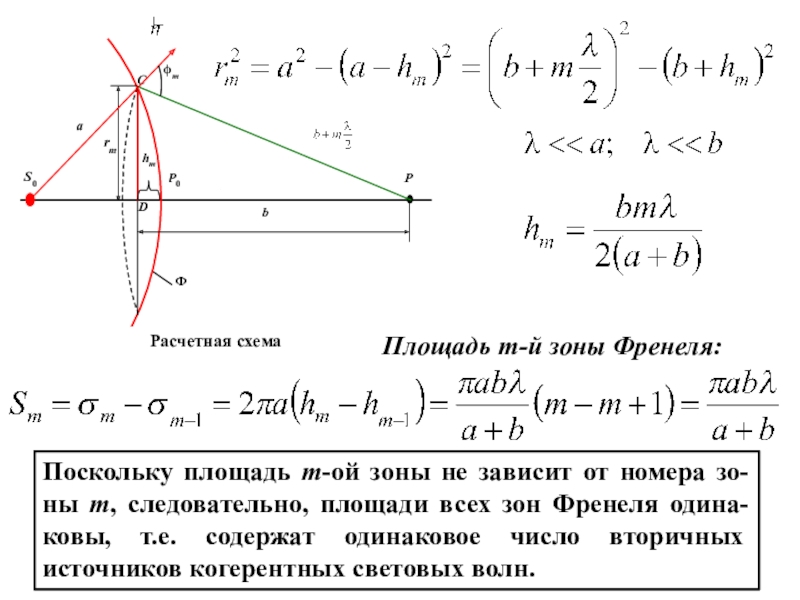
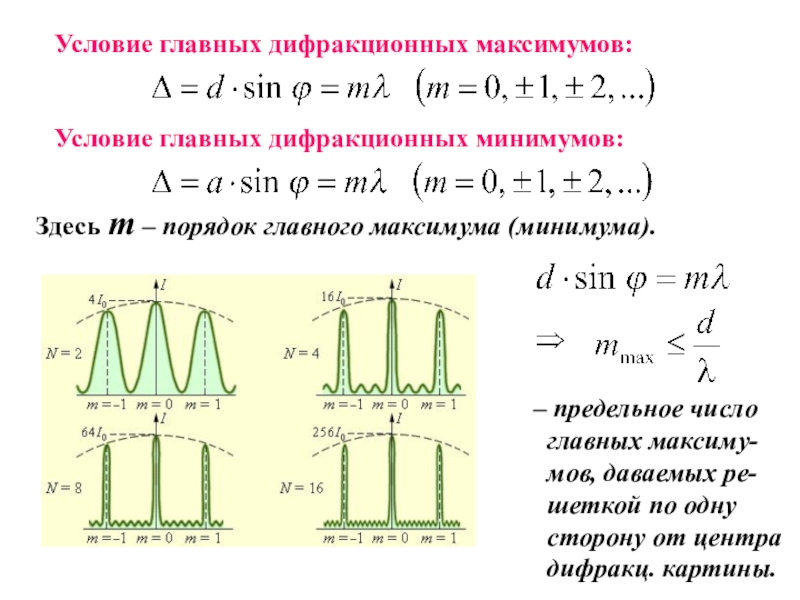
среде с резкими неоднород-ностями (вблизи границ непрозрачных тел, сквозь малые

Дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени.

распро-страняющихся вперед по всем на-правлениям, в том числе и в

Французский ученый Огюст Френель дополнил принцип
Гюйгенса идеей об интерференции вторичных волн и при-
дал ему физическое содержание.

Принцип Гюйгенса-Френеля: свето-
вая волна, возбуждаемая источником
света, в любой точке может быть
представлена как результат интерфе-
ренции когерентных вторичных волн,
излучаемых фиктивными источниками
на волновой поверхности.

источниками коге-
рентных вторичных световых
волн, которые действуют в
противофазе друг с

Р1Р Р0Р = Р2Р P1P =… = /2

А = А1  А2 + А3  А4 + …

– амплитуда результирующего
светового колебания в точке Р.

Таким образом, действие сферической световой волны от точечного источника S0 заменяется действием фиктивных
источников когерентных вторичных волн.

номера зо-ны m, следовательно, площади всех зон Френеля одина-ковы, т.е.

вызываемые в точке Р полностью откры-
той сферической волновой поверхностью, имеют

распростра-
няется в пределах очень узкого прямого канала, т.е. прямо-
линейно.
Справедливость метода

Зонные пластинки резко усиливают интенсивность проходя-
щего света, напр., если открыты 1-я, 3-я и 5-я зоны, то I≈36I0.

до точки наблюдения;
λ – длина волны света.
– критерий дифракции (по

Характерные размеры задачи:

дифракция Фраунгофера (или дифракция
в параллельных лучах).
2.

– дифракция Френеля (или дифракция
в сходящихся лучах).

3. >> 1

– случай геометрической оптики.

Дифракция Френеля на круглом отверстии

m зон на отверстии:

Знак «+» при нечетном m –
в центре дифракционной кар-
тины светлое пятно.
2) Знак «–» при четном m –
в центре дифракционной кар-
тины темное пятно.

картины (точка Р ) при любом (как четном, так и

Опыт по дифракции на диске, про-демонстрированный на заседании Парижской Академии наук в 1818 г. и доказавший наличие светлого пятна в центре тени, отбрасываемой
диском, принес всеобщее признание волновой теории света.

между крайними лучами FC и OE.
– число зон Френеля,

Условие дифракционных минимумов
(число z – четное):

Условие дифракционных максимумов
(число z – нечетное):

параллельных щелей
равной ширины, лежащих в од-ной плоскости и разделенных
равными

– период решетки.

У современных решеток приходится до (1/d) = 2000 штрихов на милли-метр.

В решетке осуществляется
многолучевая интерференция
когерентных дифрагированных
пучков света от всех щелей.

главного максимума (минимума).
– предельное число
главных максиму-
мов, даваемых ре-

ловое расстояние между двумя спек-
тральными линиями, отличающимися

2. Разрешающая способность R определяет минимальную раз-
ность близких длин волн δλmin, при которой две линии воспри-
нимаются в спектре раздельно: