Лекція 24. Точнісні показники стежачого ЕП в типових режимах роботи з різними

з різними типами регуляторів контурів швидкості та положення

Основним показником якості

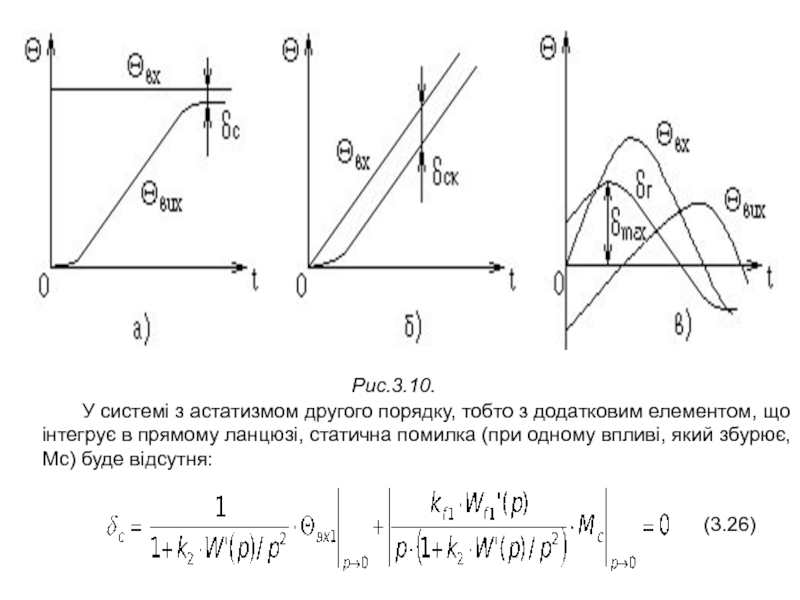
стежачих СУЕП є точність, з якої вихідний вал “слідкує” за рухом валу, що задає (будемо розглядати тільки відпрацювання зовнішніх переміщень). Точність тут оцінюється сумарною помилкою δ=δуст+δвіл, що визначається:
помилкою, що встановилася

вільною складовою помилкою δвіл при типових зовнішніх впливах, близьких до реальних впливів, що збурюють і задають у нормальних або найбільш важких режимах роботи систем.
Природно, що чим менша помилка δ, тим вища якість стежачої системи.
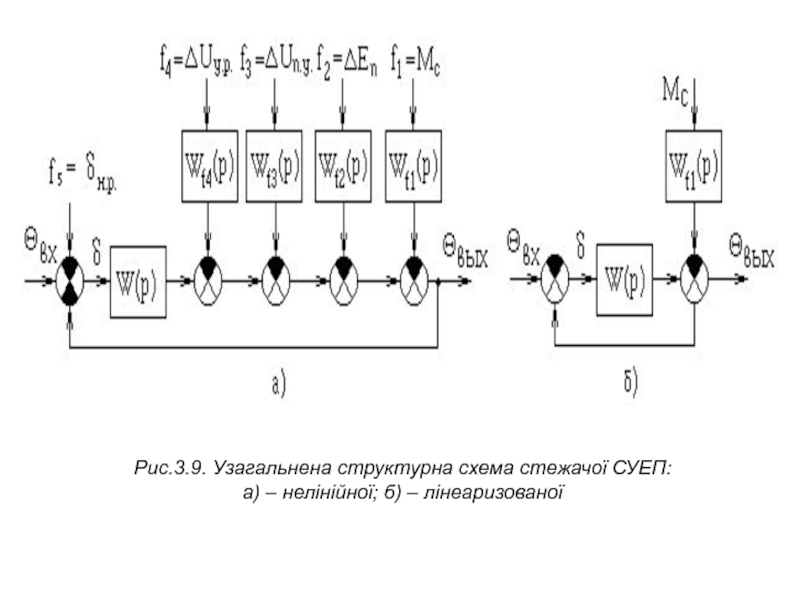
Візьмемо узагальнену структурну схему стежачої СУЕП (рис.3.9,а). До такої схеми можуть бути наведені після відповідних перетворень практично всі реальні структурні схеми лінеаризованих безперервних систем (а також імпульсних і цифрових систем, коли ці системи можна представити еквівалентними безперервними системами).

лінеаризованої

за каналом керування;
Wfi(p) = Θвих(р)/fi(р) – передавальна функція ділянки розімкненої

системи між точкою дотику і-го впливу, що збурює fі(t), і виходом системи.
Передавальна функція помилки δД замкненої системи по впливу, що задає, для схеми рис.3.9,а:

(3.16)

Передавальна функція помилки δfi замкненої системи за і-им впливом,
що збурює:

(3.17)

На основі принципу суперпозиції з допомогою передавальних функцій (3.16) і (3.17) отримаємо зображення сумарної помилки:

(3.18)

момент навантаження, тобто f1=Мс. До інших впливів, що обурюють, можна

віднести, наприклад, відхилення ЕРС силового перетворювача (f2=ΔΕп) і вихідних напруг підсилювачів ПУ й УР (відповідно f3=ΔUп.у. та f4=ΔUу.р.), збумовлені нестабільністю статичних характеристик вихід–вхід цих елементів.
Впливами, що збурюють, є також різноманітні ”шуми”, зокрема гармонійні складові випрямленої напруги тиристорних перетворювачів.
Похибка у вимірника розузгодження δі.р. можна розглядати так само, як і деякий вплив, що збурює f5=δі.р., доданий до входу системи.
Розглянемо в загальному вигляді встановлені режими систем, що стежать при типових впливах.
Приймемо для простоти, що в системі існує один постійний вплив, який збурює f1=Мс, тобто використаємо структурну схему на рис.3.9,б.
У якості типових впливів, що задають, звичайно беруть впливи наступного виду:
стрибкоподібна модифікація вхідного кута Θвх(t)=Θвх.1∙1(t), де Θвх.1=const;
рівномірна заводка Θвх(t)=ωвх.1∙t∙1(t), де ωвх.1= const;
заводка з постійним прискоренням Θвх(t)=εвх.1∙t2/2, де прискорення εвх.1= const;
“синусоїдальна” заводка Θвх(t) = Θвх max∙sinωк∙t, де Θ вх.max= const.
Похибка системи, що встановилася, визначається з виразу (3.18) при р→0:

оскільки Θвих=f∙ωвих∙dt (де ωвих – швидкість вихідного вала), що відповідає

ланці, яка інтегрує з передавальною функцією 1/р у прямому ланцюзі системи. Тоді передавальні функції системи можна уявити в такому вигляді:

(3.20)

(3.21)

Множники, які входять у вирази W'(p) і Wf1′(р), звичайно є передавальними функціями елементарних ланок (аперіодичних, коливальних, що диференціюють).
Коефіцієнт k1 являє собою коефіцієнт передачі розімкненої системи за каналом керування.
Коефіцієнт kf1 є коефіцієнтом передачі розімкненої системи за впливом, що збурює (в даному випадку за моментом навантаження).
Включення елементів, що інтегрують у прямий ланцюг системи, призводить до підвищення порядку її астатизму. Якщо такий елемент (наприклад, обладнання, що корегує) буде мати передавальну функцію виду k1/р, то

(3.21).
Режим, що встановився після відпрацювання стрибка кута завдання Θвх.1 (рис.3.10,а),

відповідає нерухомому стану вихідного вала. В цьому випадку виявлену помилку системи, що стежить, називають статичною помилкою δс.
Для системи з астатизмом першого порядку, враховуючи (3.20) і (3.21), з виразу (3.19) знаходимо:

(3.23)

При р→0 отримаємо, що W'(p)→ 1, Wf1′ (р)→1. Перший додаток у (3.23)
перетворюється в нуль і

(3.25)

де Dм – k1/kf1 – добротність системи, що стежить, за моментом, тобто відношення моменту навантаження до зумовленої ним помилки δс.

що інтегрує в прямому ланцюзі, статична помилка (при одному впливі,

який збурює, Мс) буде відсутня:

(3.26)

заводки
При цьому ωвих.уст. = ωвх.1 = const.
Із виразу (3.19) при

Θвх(р)=ωвх.1/р з урахуванням (3.20) і (3.21) знаходимо:

(3.27)

Другий додаток (3.27) дасть статичну помилку δс, що визначається співвідношенням (3.24). Перший додаток являє собою
так звану швидкісну помилку:

(3.28)

Розглядуваний режим ілюструє рис.3.10,б, на якому прийнято, що δс=0. Оскільки система може рухатися з різними швидкостями, то якість її в режимі рівномірної заводки більш зручно характеризувати не самою швидкісною помилкою, що є змінною величиною, а відношенням швидкості задання до зумовленої ним помилки – добротністю СЕП за швидкістю:

(3.29)

(3.28)

встановилася з астатизмом k1 першого порядку в режимі рівномірної заводки:
(3.30)

У системі з астатизмом другого порядку не тільки δс = 0, але і δск = 0.

Режим руху СС із постійним прискоренням

При цьому εвих.уст. = εвх.1 = const.
Даний режим має сенс тільки для систем з астатизмом другого порядку. Для таких систем δс = 0 (якщо мати один вплив Мс, що збурює). Отже,виявлена помилка визначається тільки впливом, що задають, Θвх(р)=εвх.1/р2. В цьому випадку вираз (3.30) має вигляд

(3.31)

Цю помилку називають помилкою системи, що стежить, від постійного
прискорення.

величиною добротності за прискоренням – відношенням прискорення до зумовленої ним

помилки:

(3.33)

причому величина Dε чисельно рівна коефіцієнту передачі системи k2.
У загальному випадкові при обліку декількох впливів, що обурюють, статичну помилку системи, що стежить, δсΣ визначають із рівняння (3.18) як Σδfi(p) при р→0. Очевидно, що навіть за наявності в прямому ланцюзі системи додаткового інтегрувального елемента в сумарній помилці залишаться складові, зумовлені впливами, що збурюють, доданими між входом системи елементом, що інтегрує.
Зокрема, підвищення порядку астатизму не дасть можливості усунути помилку, зумовлену похибкою вимірника розузгодження δі.р.. Це легко показати, визначаючи складову сумарної статичної помилки від дії збурення f5=δі.р.. Згідно із схемою (рис.3.9,а), Wf5(р)=W (р). Тоді при будь-якому

порядкові астатизму, тобто при

при р→0, отримаємо: