Лекція № 2 (1) Елементи механіки пружного анізотропного тіла

багатошарових конструкцій типовим є плоский напружений стан і деформації згинання,

тому важливим є питання переходу від загальних фізичних співвідношень для лінійного пружного анізотропного тіла до конкретних форм його запису для цих напружених станів. Особливо важливі питання пов’язані з характеристиками механічних властивостей односпрямованого матеріалу, основного елемента сучасних силових тонкостінних оболонок, і їх перетворенням у зведені характеристики багатошарових матеріалів, складених із різноорієнтованих шарів односпрямованих матеріалів.

2.1. Узагальнений закон Гука

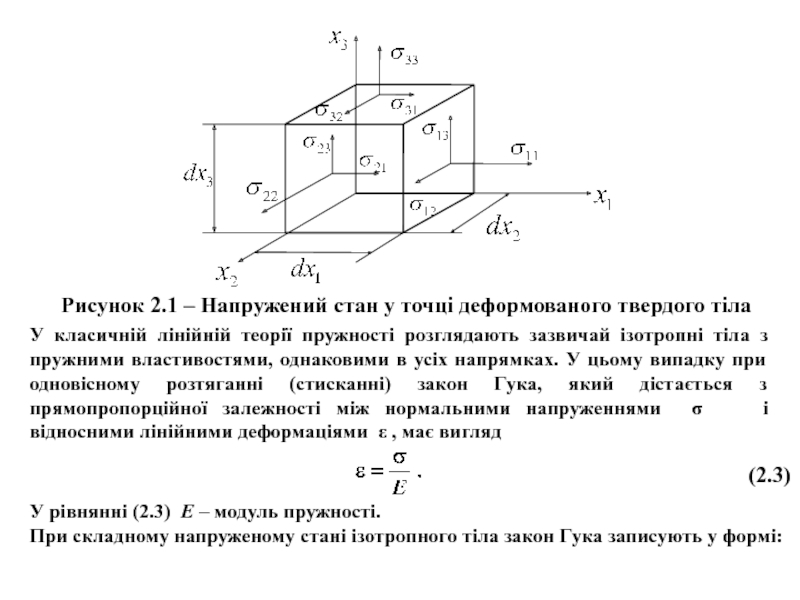
Розглянемо деформоване тіло в декартовій системі координат x1, x2, x3 (рис. 2.1).
На рис. 2.1 прийняті позначення: , (i, j = 1, 2, 3) – нормальні й дотичні
напруження відповідно.
Компоненти тензора деформацій визначимо лінійними співвідношеннями:

(2.1)

де u1, u2, u3 – проекції повного переміщення на координатні осі x1, x2, x3
відповідно. Внаслідок закону парності дотичних напружень і структури рівнянь
(2.1) виконуються тотожності

(2.2)

У класичній лінійній теорії пружності розглядають зазвичай ізотропні тіла з

пружними властивостями, однаковими в усіх напрямках. У цьому випадку при одновісному розтяганні (стисканні) закон Гука, який дістається з прямопропорційної залежності між нормальними напруженнями σ і відносними лінійними деформаціями ε , має вигляд

(2.3)

У рівнянні (2.3) Е – модуль пружності.
При складному напруженому стані ізотропного тіла закон Гука записують у формі:

3) – компоненти тензора напружень; ν - коефіцієнт Пуассона;

G – модуль зсуву, або модуль пружності другого роду. Відомо, що технічні сталі E, G
і ν пов’язані формулою

(2.4)

Кути зсуву , що входять у співвідношення (2.4), можна записати за допомогою
компонент тензора деформацій:

(2.5)

Незалежні компоненти тензора напружень і тензора деформації, як правило, записуються у
формі матриць-стовпців:

(2.6)

деформацій таким чином:
(2.7)
Тоді узагальнений закон Гука для ізотропного тіла в

матричній формі має такий вигляд:

(2.8)

Матриця піддатливості [B], що входить до рівняння (2.8), у розгорнутій формі запишеться так:

(2.9)

Найважливішою особливістю закону Гука для ізотропного тіла є та обставина, що матриця піддатливості (2.9) інваріантна до вибору систем координат і формується із використанням лише двох незалежних констант – Е і ν, які повністю визначають пружні властивості ізотропного тіла.

Деформації зсуву залежать лише від дотичних напружень τij, тому для пружного ізотропного тіла головні вісі напруженого стану завжди збігаються із головними осями деформованого стану.

деформацій зміна будь-якої компоненти тензора напружень σij може привести до

виникнення всіх компонент εij тензора деформації. Наприклад, якщо призматичний брус, виготовлений із анізотропного матеріалу, рівномірно розтягувати вздовж осі, то в загальному випадку анізотропії такий брус, крім подовжень вздовж осі й зміни розмірів поперечного перерізу, буде зазнавати деформації зсуву у всіх трьох площинах прийнятої декартової системи координат, що призводять до зміни кутів між гранями (початково прямих до деформації).
Узагальнений закон Гука для анізотропного тіла можна сформулювати так: у кожній точці тіла компоненти тензора деформації εij є однорідними лінійними функціями компонент σij тензора напружень. У матричній формі (2.8) зазначені залежності можна подати так:

(2.10)

де

матриця піддатливості анізотропного матеріалу, її компоненти називають коефіцієнтами піддатливості.

(2.11)

6х6. Неважко показати, що внаслідок теореми про взаємність робіт для

компонент матриці піддатливості

Тому в матриці [B] незалежним є лише 21 коефіцієнт, тобто

(2.12)

Узагальнений закон Гука для анізотропного тіла можна записати у вигляді лінійної залежності напружень від деформацій:

де [A] – матриця жорсткості матеріалу розміром 6х6.
Компоненти матриці [A] можна записати за допомогою компонент матриці піддатливості [B], розв’язуючи систему рівнянь (2.10) відносно напружень {σ}:

(2.13)

(2.14)

Зіставивши рівняння (2.13) і (2.14), неважко встановити зв’язок між матрицями піддатливості та жорсткості:

(2.15)

містить 21 незалежний коефіцієнт, трапляється рідко. Зазвичай структура реального композита

така, що його пружні властивості у деяких напрямах однакові. В цьому випадку кількість незалежних коефіцієнтів у матриці піддатливості зменшується і при належному виборі системи координат спрощується запис закону Гука.
П л о щ и н а п р у ж н о ї с и м е т р і ї. Якщо в анізотропному тілі його пружні властивості ідентичні в будь-яких двох напрямах, симетричних відносно деякої площини, тоді така площина називається площиною пружної симетрії. В цьому випадку кількість коефіцієнтів матриці [B] зменшується до 13, а закон Гука набирає більш простого вигляду при суміщенні однієї з координатних площин із площиною пружної симетрії. Наприклад, при суміщенні координатної площини x1Ox2 із площиною пружної симетрії матриця піддатливості (2.12) матиме вигляд

(2.16)

У частині одновісного розтягання анізотропного тіла у напрямі, перпендикуляр-ному до площини пружної симетрії, спостерігаються співвідношення:

площині пружної симетрії. Таким чином, якщо одна із головних осей

напруженого стану перпендикулярна до площини пружної симетрії, тоді й одна із головних осей деформованого стану також буде перпендикулярна до цієї площини. Тому напрям, перпендикулярний до площини пружної симетрії, називають головним напрямом, або головною віссю пружності.

О р т о т р о п н и й м а т е р і а л. Якщо в анізотропному тілі існують дві взаємно перпендикулярні площини пружної симетрії, тоді неважко довести, що перпендикулярна до них площина буде також площиною пружної симетрії. Нехай дві головні осі напруженого стану перпендикулярні до двох площин пружної симетрії, які є в розглянутому тілі, тобто збігаються із двома головними напрямами пружності матеріалу. Тоді з цими напрямами збігатимуться і дві головні осі деформованого стану. Таким чином, третя головна вісь деформованого стану також збігатиметься з третьою головною віссю напруженого стану, і перпендикулярна до них площина буде площиною пружної симетрії тіла.
Тіло, що має три взаємно перпендикулярні площини пружної симетрії, називають ортотропним.
Для ортотропного тіла кількість незалежних коефіцієнтів, що характеризують пружний стан тіла, дорівнює 9. Закон Гука для ортотропного тіла найбільш просто записується при суміщенні координатних площин із площинами пружної симетрії. Матриця піддатливості (2.12) набирає вигляду

їх записати за допомогою технічних сталих (модулів пружності, модулів зсуву,

коефіцієнтів Пуассона), тобто

(2.17*)

x1, x2, x3 ; G23, G13, G12 – модулі зсуву

відповідно у площинах x20x3, x10x3, x10x2; νij – коефіцієнт Пуассона, перший індекс вказує на напрям діючого напруження, а другий – на напрям поперечної деформації, що виникає при цьому.
Число незалежних параметрів у (2.17*) зберігається, тобто дорівнює 9, оскільки внаслідок симетрії матриці піддатливості виконуються тотожності:

(2.18*)

Зі співвідношень (2.18) неважко отримати такий вираз:

Наведена вище система запису технічних сталих не є одноосібною.
Відмітимо один випадок ортотропного тіла, в якому пружні властивості однакові у всіх трьох напрямах головних осей пружності. При цьому кількість незалежних коефіцієнтів жорсткості скорочується до трьох. Якщо для опису пружних властивостей такого ортотропного тіла скористатися технічними сталими, то у виразах (2.17*), (2.18) і (2.18*)

(2.19)

На відміну від ізотропного тіла в цьому частковому випадку технічні сталі E, G, ν є незалежними величинами, що характеризують пружні властивості матеріалу.
Для ортотропного тіла, якщо закон Гука записати у вигляді (2.13), коефіцієнти матриці жорсткості неважко також визначити за допомогою технічних сталих:

л ь н о – і з о т р

о п н е тіло. Площину, в якій пружні властивості у всіх напрямах ідентичні, називають площиною ізотропії, а тіло, що має таку площину, називають трансверсально-ізотропним.
Кількість незалежних коефіцієнтів, що характеризують пружні властивості тіла дорівнює п’яти. Нехай координатна площина x10x2 збігається з площиною ізотропії, тоді отримаємо такі вирази для матриці піддатливості:

і у напрямі перпендикулярному до площини ізотропії відповідно;

модуль зсуву;

модуль зсуву;

ν3 – коефіцієнти Пуассона, що характеризують поперечні деформації у відповідних

площинах, перпендикулярних до напрямів дії відповідних нормальних напружень. У трансверсально-ізотропному тілі всі напрями в площині ізотропії, а також у напрямі, перпендикулярному до цієї площини є головними напрямами пружності. Тому для такого тіла головні осі деформованого стану збігаються з головними осями напруженого стану, якщо одна з головних осей напруженого стану перпендикулярна до площини ізотропії.