Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекція № 2 (2) Зведені характеристики механічних властивостей односпрямованого
Содержание
- 1. Лекція № 2 (2) Зведені характеристики механічних властивостей односпрямованого
- 2. Визначення деформаційних характеристик композиційних
- 3. Рисунок 2.2 – Плоский напружений стан у
- 4. (2.22)Індекси “в” та “м” вказують, що компонента
- 5. (2.26)Зі співвідношень (2.22) і (2.25) з’ясовується, що
- 6. абоДля о р т о т р
- 7. Для анізотропного тіла коефіцієнти піддатливості утворюють повністю
- 8. Анізотропія загального вигляду в реальних матеріалах, коли
- 9. За такого напруженого стану матеріал зазнає деформації
- 10. (2.17)Фізичний зміст коефіцієнтів піддатливості матриці (2.17) стає
- 11. (2.18)Тут E1, E2, E3 – модулі пружності
- 12. (2.20)Т р а н с в е
- 13. (2.21)або (2.22)Тут E1, E3 – модулі пружності
- 14. модуль зсуву у площинах, перпендикулярних до площини
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 Лекція № 2 (2) Зведені характеристики механічних властивостей односпрямованого матеріалу.
Методи зведення
Слайд 2Визначення деформаційних характеристик композиційних матеріалів властивостями
компонентів (армуючий матеріал, матриця) і характером
їх розташування в матеріалі становить одну з основних задач теорії армування.В основу наближених розрахунків за Фойгтом і Рейсом пружних характеристик композиційних матеріалів покладений принцип підсумовування повторюваних елементарних шарів. Пружні характеристики елементарного шару визначають у два етапи [1, 7 – 9]. Спочатку знаходять характеристики зведеної матриці за рахунок усереднення пружних властивостей волокон ортогонально-армованого матеріалу шару. Вважають, що компоненти матеріалу (волокно й матриця) ізотропні, лінійно пружні й працюють спільно на всіх етапах деформування. Крім того, прийняті припущення, згідно з якими: не враховуються напруження, перпендикулярні до волокон під час дії нормального навантаження вздовж волокон; поперечні деформації при розтяганні – стисканні кожного компонента пропорційні її об’ємному вмісту в матеріалі; на поверхні волокно-матриця виключається розгляд концентрації напружень. На другому етапі здійснюють розрахунки характеристик шару, виходячи із пружних властивостей волокон і модифікованої матриці.
Експериментальні дані добре збігаються зі значеннями пружних характеристик композиційних матеріалів, обчислених на основі методів [1, 7 – 9].
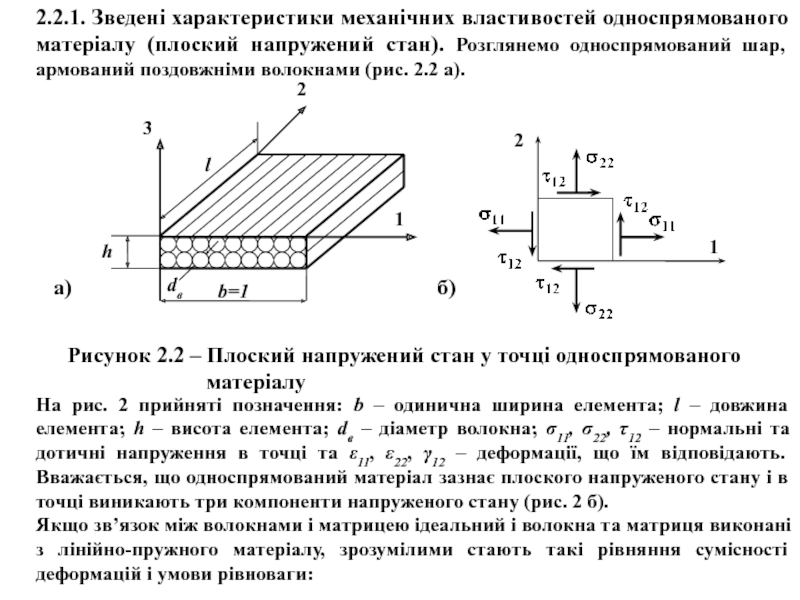
Слайд 3Рисунок 2.2 – Плоский напружений стан у точці односпрямованого
матеріалу
2.2.1. Зведені характеристики механічних властивостей односпрямованого матеріалу (плоский напружений стан). Розглянемо односпрямований шар, армований поздовжніми волокнами (рис. 2.2 а).
б)
На рис. 2 прийняті позначення: b – одинична ширина елемента; l – довжина елемента; h – висота елемента; dв – діаметр волокна; σ11, σ22, τ12 – нормальні та дотичні напруження в точці та ε11, ε22, γ12 – деформації, що їм відповідають. Вважається, що односпрямований матеріал зазнає плоского напруженого стану і в точці виникають три компоненти напруженого стану (рис. 2 б).
Якщо зв’язок між волокнами і матрицею ідеальний і волокна та матриця виконані з лінійно-пружного матеріалу, зрозумілими стають такі рівняння сумісності деформацій і умови рівноваги:
Слайд 4(2.22)
Індекси “в” та “м” вказують, що компонента напружено-деформованого стану належить
до волокна або до матриці відповідно.
Установимо зв'язок між напруженнями та
деформаціями у волокні та матриці з середніми напруженнями у композиті, а також зв'язок між пружними характеристиками волокна і матриці та зведеними або ефективними характеристиками композита.При розгляді деформування односпрямованого матеріалу вздовж волокон, в ортогональному напрямку і зсуві у площині шару спостерігаються такі залежності:
(2.23)
які відображають так зване “правило сумішів”. Згідно із цим правилом внесок кожної компоненти розглянутого напружено-деформованого стану пропорційний її об’ємному вмісту в композиційному матеріалі. У формулах (2.23) позначено: ψ – об’ємна частка волокна; (1- ψ ) – об’ємна частка матриці.
Запишемо закон Гука для волокна та матриці, вважаючи їх ізотропними матеріалами:
(2.24)
Слайд 5(2.26)
Зі співвідношень (2.22) і (2.25) з’ясовується, що напруження у волокні
та матриці можна записати через середні напруження у композиті:
(2.27)
(2.25)
(2.29)
(2.30)
(2.28)
Для середніх
деформацій можуть бути отримані такі співвідношення:Порівняємо співвідношення (2.28) – (2.30) із законом Гука (2.10), (2.17*). Для ортотропного тіла при плоскому напруженому стані, коли
цей закон збігається із законом Гука.
Слайд 6або
Для о р т о т р о п н
о г о т і л а із
площиною ізотропії 102 (рис. 2.2 а) він запишеться у такому вигляді:(2.31)
Тепер нескладно знайти вираз технічних сталих для односпрямованого композита:
(2.37)
(2.32)
Нехтуючи доданками, що мають порядок квадрата коефіцієнтів Пуассона порівняно із одиницею, з виразу (2.33) отримаємо
(2.33)
Для модуля зсуву маємо аналогічну за структурою формулу
де
(2.34)
(2.35)
Коефіцієнти Пуассона односпрямованого матеріалу мають вигляд
(2.36)
Слайд 7Для анізотропного тіла коефіцієнти піддатливості утворюють повністю заповнену матрицю розміром
6х6. Неважко показати, що внаслідок теореми про взаємність робіт для
компонент матриці піддатливостіТому в матриці [B] незалежним є лише 21 коефіцієнт, тобто
(2.12)
Узагальнений закон Гука для анізотропного тіла можна записати у вигляді лінійної залежності напружень від деформацій:
де [A] – матриця жорсткості матеріалу розміром 6х6.
Компоненти матриці [A] можна записати за допомогою компонент матриці піддатливості [B], розв’язуючи систему рівнянь (2.10) відносно напружень {σ}:
(2.13)
(2.14)
Зіставивши рівняння (2.13) і (2.14), неважко встановити зв’язок між матрицями піддатливості та жорсткості:
(2.15)
Слайд 8Анізотропія загального вигляду в реальних матеріалах, коли матриця піддатливості [B]
містить 21 незалежний коефіцієнт, трапляється рідко. Зазвичай структура реального композита
така, що його пружні властивості у деяких напрямах однакові. В цьому випадку кількість незалежних коефіцієнтів у матриці піддатливості зменшується і при належному виборі системи координат спрощується запис закону Гука.П л о щ и н а п р у ж н о ї с и м е т р і ї. Якщо в анізотропному тілі його пружні властивості ідентичні в будь-яких двох напрямах, симетричних відносно деякої площини, тоді така площина називається площиною пружної симетрії. В цьому випадку кількість коефіцієнтів матриці [B] зменшується до 13, а закон Гука набирає більш простого вигляду при суміщенні однієї з координатних площин із площиною пружної симетрії. Наприклад, при суміщенні координатної площини x1Ox2 із площиною пружної симетрії матриця піддатливості (2.12) матиме вигляд
(2.16)
У частині одновісного розтягання анізотропного тіла у напрямі, перпендикуляр-ному до площини пружної симетрії, спостерігаються співвідношення:
Слайд 9За такого напруженого стану матеріал зазнає деформації зсуву тільки у
площині пружної симетрії. Таким чином, якщо одна із головних осей
напруженого стану перпендикулярна до площини пружної симетрії, тоді й одна із головних осей деформованого стану також буде перпендикулярна до цієї площини. Тому напрям, перпендикулярний до площини пружної симетрії, називають головним напрямом, або головною віссю пружності.О р т о т р о п н и й м а т е р і а л. Якщо в анізотропному тілі існують дві взаємно перпендикулярні площини пружної симетрії, тоді неважко довести, що перпендикулярна до них площина буде також площиною пружної симетрії. Нехай дві головні осі напруженого стану перпендикулярні до двох площин пружної симетрії, які є в розглянутому тілі, тобто збігаються із двома головними напрямами пружності матеріалу. Тоді з цими напрямами збігатимуться і дві головні осі деформованого стану. Таким чином, третя головна вісь деформованого стану також збігатиметься з третьою головною віссю напруженого стану, і перпендикулярна до них площина буде площиною пружної симетрії тіла.
Тіло, що має три взаємно перпендикулярні площини пружної симетрії, називають ортотропним.
Для ортотропного тіла кількість незалежних коефіцієнтів, що характеризують пружний стан тіла, дорівнює 9. Закон Гука для ортотропного тіла найбільш просто записується при суміщенні координатних площин із площинами пружної симетрії. Матриця піддатливості (2.12) набирає вигляду
Слайд 10(2.17)
Фізичний зміст коефіцієнтів піддатливості матриці (2.17) стає більш зрозумілим, якщо
їх записати за допомогою технічних сталих (модулів пружності, модулів зсуву,
коефіцієнтів Пуассона), тобто(2.17*)
Слайд 11(2.18)
Тут E1, E2, E3 – модулі пружності у відповідному напрямі
x1, x2, x3 ; G23, G13, G12 – модулі зсуву
відповідно у площинах x20x3, x10x3, x10x2; νij – коефіцієнт Пуассона, перший індекс вказує на напрям діючого напруження, а другий – на напрям поперечної деформації, що виникає при цьому.Число незалежних параметрів у (2.17*) зберігається, тобто дорівнює 9, оскільки внаслідок симетрії матриці піддатливості виконуються тотожності:
(2.18*)
Зі співвідношень (2.18) неважко отримати такий вираз:
Наведена вище система запису технічних сталих не є одноосібною.
Відмітимо один випадок ортотропного тіла, в якому пружні властивості однакові у всіх трьох напрямах головних осей пружності. При цьому кількість незалежних коефіцієнтів жорсткості скорочується до трьох. Якщо для опису пружних властивостей такого ортотропного тіла скористатися технічними сталими, то у виразах (2.17*), (2.18) і (2.18*)
(2.19)
На відміну від ізотропного тіла в цьому частковому випадку технічні сталі E, G, ν є незалежними величинами, що характеризують пружні властивості матеріалу.
Для ортотропного тіла, якщо закон Гука записати у вигляді (2.13), коефіцієнти матриці жорсткості неважко також визначити за допомогою технічних сталих:
Слайд 12(2.20)
Т р а н с в е р с а
л ь н о – і з о т р
о п н е тіло. Площину, в якій пружні властивості у всіх напрямах ідентичні, називають площиною ізотропії, а тіло, що має таку площину, називають трансверсально-ізотропним.Кількість незалежних коефіцієнтів, що характеризують пружні властивості тіла дорівнює п’яти. Нехай координатна площина x10x2 збігається з площиною ізотропії, тоді отримаємо такі вирази для матриці піддатливості:
Слайд 13(2.21)
або
(2.22)
Тут E1, E3 – модулі пружності в площині ізотропії
і у напрямі перпендикулярному до площини ізотропії відповідно;
модуль зсуву;модуль зсуву;






![Лекція № 2 (2) Зведені характеристики механічних властивостей односпрямованого Анізотропія загального вигляду в реальних матеріалах, коли матриця піддатливості [B] містить Анізотропія загального вигляду в реальних матеріалах, коли матриця піддатливості [B] містить 21 незалежний коефіцієнт, трапляється рідко. Зазвичай](/img/tmb/3/290392/1052ea88bd0c114f0cec3945ab174bad-800x.jpg)