Линейность преобразования координат

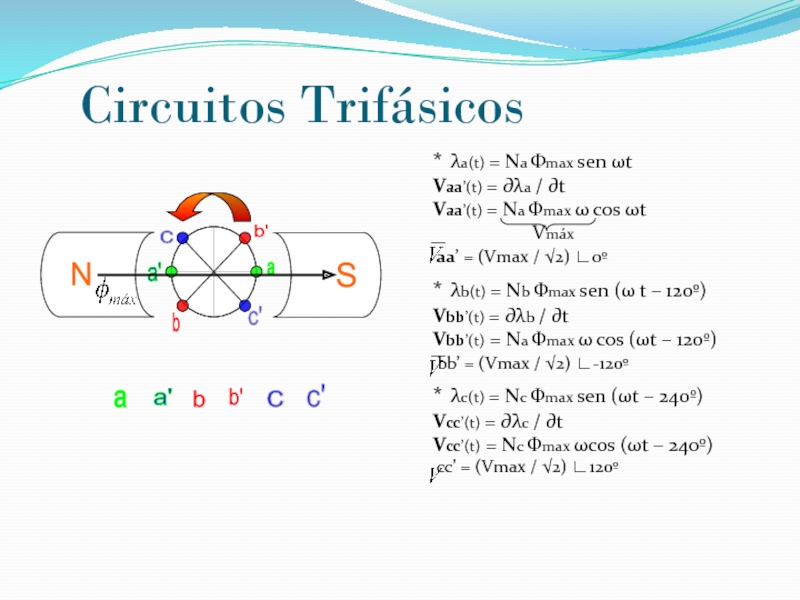
выводам, противоречащим экспериментам, и постоянство скорости света не является их

следствием, они не отражают правильно той связи, которая существует для координат и времени инерциальных систем координат, движущихся друг относительно друга. Необходимо найти другие преобразования, которые правильно описывают экспериментальные факты и, в частности, приводят к постоянству скорости света. Эти преобразования называются преобразованиями Лоренца. Они могут быть введены исходя из двух принципов, обоснование которых было изложено в предыдущих параграфах:
принципа относительности;
принципа постоянства скорости света.
Оба эти принципа, хотя и подтверждены многочисленными экспериментами, имеют характер постулатов и поэтому иногда называются постулатом относительности и постулатом постоянства скорости света.

сводящимися к пространственным поворотам и переносам начала координат в пределах

каждого из тел отсчета, можно всегда привести к такой, которая изображена на рис. 26. Поскольку скорости не скла­дываются по классической формуле (12.10), можно ожидать, что время одной системы координат не выражается только через время другой системы координат, а зависит также и от координат. Поэтому в общем случае преобразования имеют следующий вид:

(6.1.1)

где в правых частях стоят некоторые функции Фь вид которых надо найти.

рассмотрении геометрических соотношений в выбранной системе отсчета и при измерениях

в ней принималось, что каждая точка ничем не отличается от любой другой точки. Это означает, что начало системы координат может быть помещено в любой точке и все геометрические соотношения между любыми геометрическими объектами при этом совершенно одинаковы с теми, которые получаются при помещении начала координат в любую другую точку. Это свойство называется однородностью пространства, т. е. свойством неизменности характеристик пространства при переходе от одной точки к другой. Можно также в каждой точке пространства оси системы координат произвольным образом ориентировать в нем, при этом геометрические соотношения между геометрическими объектами также не изменяются. Это означает, что свойства пространства по различным направлениям одинаковы. Такое свойство называется изотропностью пространства.

системах координат.
Время также обладает важнейшим свойством однородности. Физически это означает

следующее. Пусть некоторая физическая ситуация возникает в некоторый момент времени. В последующие моменты времени она будет каким-то образом развиваться. И пусть такая же физическая ситуация возникает в любой другой момент времени. Если она в последующие моменты времени будет развиваться относительно этого момента точно так же, как она в первом случае развивалась относительно своего начального момента, то говорят, что время однородно. Иначе говоря,
однородность времени есть одинаковость развития и изменения данной физической ситуации независимо от того, в какой момент времени эта ситуация сложилась.

быть линейными. Для доказательства рассмотрим бесконечно малое изменение dx' ,

т. е. разность координат х' двух бесконечно близких точек. В нештрихованной системе им будут соответствовать бесконечно малые разности координат dx, dy, dz и времени dt. Из (14.1) можно вычислить полное изменение dx', связанное с изменениями величин х, у, z, t, по формуле полного дифференциала, известной из математики:

В силу однородности пространства и времени эти соотношения должны быть одинаковыми для всех точек пространства и для любых моментов времени. А это означает, что величины дФ1/дх, дФ1/ду, дФ1/dz, дФ1/dt не должны зависеть от координат и времени, т. е. являются постоянными. Поэтому функция Ф1 имеет следующий вид:

(6.1.2)

(6.1.3)

образом, функция Ф1 (х,y,z,t) является линейной функцией своих аргументов. Аналогично

доказывается, что в силу однородности пространства и времени и другие функции Ф2, Ф3 и Ф4 в преобразованиях (6.1.1) будут линейными функциями от х, у, z, t.

6.1.3.Преобразования для у и z. Точка начала в каждой системе координат задается равенствами х = у = z = 0, х' = у' = z' = 0. Будем считать, что в момент t = 0 начала координат совпадают. Тогда свободный член A5 в линейных преобразованиях вида (6.1..3) должен быть равен нулю и преобразования для у и z запишутся следующим образом

Ориентировка осей координат указана на рис. 4.1: ось у' параллельна оси у, а ось z — оси z. Поскольку ось х' все время совпадает с осью х, из условия у = 0 всегда следует равенство у' = 0, а из условия z = 0 — равенство z' = 0, т. е. должно быть

(6.1.4)

лишь при условии
а1 = а3 = а4 = 0,

b1== b2 = b4 = 0.

(6.1.6)

Поэтому преобразования для у и z принимают следующий простой вид:

(6.1.7)

где учтено, что в силу равноправности осей у и z относительно движения коэффициенты в преобразованиях должны быть одинаковыми: у3 = bз = а. Коэффициент а в формуле (6.1.7) показывает, во сколько раз длина некоторого масштаба в штрихованной системе координат больше, чем в нештрихованной. Перепишем (6.1.7) в виде

(6.1.8)

нештрихованной системе больше, чем в штрихованной. Согласно принципу относительности, обе

системы координат равноправны и поэтому при переходе от одной системы к другой длина масштаба должна изменяться так же, как и при обратном переходе. Поэтому в формулах (14.7) и (14.8) должно соблюдаться равенство (1/а) = а, откуда получаем а = 1 (возможное математически решение а = -1 исключается в силу выбранной ориентации осей: положительные значения осей y, z и у', z' совпадают). Следовательно, преобразования для координат у и z имеют вид:

(6.1.9)

6.1.4.Преобразования для х и t. Поскольку переменные у и z преобразуются отдельно, переменные х и t могут быть связаны линейным преобразованием только друг с другом. Точка начала движущейся системы координат в неподвижной имеет координату х = υt,
а в движущейся системе — координату х' = 0. Поэтому в силу линейности преобразования должно быть

(6.1.10)

α = α'.
Пусть некоторый стержень покоится в штрихованной системе координат

и имеет в ней длину l. Это означает, что координаты начала и конца стержня различаются в этой системе на величину l:

где α — коэффициент пропорциональности, который требуется определить.

Совершенно аналогичные рассуждения можно провести, отправ­ляясь от движущейся системы, приняв ее за покоящуюся. Тогда в ней точка начала координат нештрихованной системы имеет коор­динату х' = - υt', поскольку в штрихованной системе нештрихованная движется в направлении отрицательных значений оси х. Точка начала координат нештрихованной системы в нештрихованной системе характеризуется равенством х = 0. Следовательно, отправляясь от штрихованной системы, как неподвижной, приходим вместо (6.1.10) к преобразованию

(6.1.11)

(6.1.12)

его считается расстояние между двумя точками неподвижной системы, с которыми

в один и тот же момент времени совпадают начало и конец движущегося стержня. Засечем концы его в момент t0. На основании формул (6.1.10) получим для координат засечек x'1 и х'2 следующие выражения:

Следовательно, длина движущегося стержня в неподвижной нештрихованной системе равна

(6.1.14)

Пусть теперь тот же стержень покоится в нештрихованной системе и имеет в ней длину l. Следовательно, координаты начала и конца стержня различаются в этой системе на величину l, т. е.

(6.1.15)

скоростью –υ. Чтобы измерить его длину относительно штрихованной системы, необходимо

засечь начало и конец этого стержня в некоторый момент t'0 этой системы. На основании формулы (6.1.11) имеем:

(6.1.16)

Следовательно, длина движущегося стержня в штрихованной системе, принятой за неподвижную, равна

(6.1.17)

Согласно принципу относительности обе системы равноправны и длина одного и того же стержня, движущегося в этих системах с одинаковой скоростью, должна быть одинаковой. Поэтому в формулах (6.1.14) и (6.1.17) должно быть (l/α) = (l/α'), т. е. α = α', что и требовалось доказать.

когда начала координат совпадают и когда часы, находящиеся в началах

координат, показывают время t = t' = 0, из них испускается световой сигнал. Распространение света в штрихованной и нештрихованной системах координат описывается равенствами:

(6.1.18)

в которых учтено, что в обеих системах скорость света имеет одно и то же значение с. Эти равенства характеризуют положение светового сигнала, распространяющегося в направлении осей х, х' в любой момент времени каждой из систем координат. Подставляя (6.1.18) в формулы (6.1.10) и (6.1.11) с учетом того, что α = α', находим:

(6.1.19)

Умножая левые и правые части этих равенств друг на. друга и сокра­щая на t't, получаем

(6.1.20)

Преобразования (6.1.9), (6.1.10) и (6.1.22) связывают между собой координаты систем,

движущихся относительно друг друга со скоростью υ. Они называются преобразованиями Лоренца. Выпишем их здесь еще раз:

(6.1.23)

лишь изменяется знак скорости:
(6.1.24)
Переход от (6.1.23) к (6.1.24) можно произвести

и без использования принципа относительности. Для этого надо равенства (6.1.23) рассмотреть как систему уравнений относительно нештрихованных величин и решить ее. В результате получаются выражения (6.1.24). Рекомендуем проделать это вычисление в качестве упражнения.

скоростей, много меньших скорости света, в преобразованиях Лоренца можно пренебречь

величинами порядка (υ/c) << 1 в сравнении с единицей, т. е. все величины υ/c в этих преобразованиях положить равными нулю. Тогда они све­дутся к преобразованиям Галилея (12.1). При малых скоростях различие между преобразованиями Лоренца и Галилея незначительно и поэтому неточность преобразований Галилея долго оставалась незамеченной.