Линейный поиск

критерия останова итеративного процесса. При этом предполагается, что условия, определяющие

направление спуска,



выполнены.

Практика показывает, что искать точное решение задачи о минимуме функции


не обязательно. Кажется, что достаточно добиться на каждой итерации выполнения условия

при фиксированных и .

, которое затем уменьшается (делением
пополам)

до момента, пока не выполнится условие ,
может привести к совершенно неправильным результатам.
Необходимо использование более строгих правил выбора параметра шага
для обеспечения сходимости метода.
Отметим, что при выборе шага хочется преодолеть две основные проблемы:
медленная скорость сходимости и малая величина шага.
Первая может быть решена требованием выполнения условия:

(*)

при .

Линейный поиск

не меньше определенной доли от величины, достигнутой на предыдущей итерации.

Чтобы шаг метода не был слишком маленьким, накладывается еще одно условие (но так, чтобы удовлетворялось и предыдущее):

(**)
при . На практике обычно выбирают
Иногда последнее неравенство заменяют более слабым:

(***)
(вспомним, что поскольку - направление спуска).

Линейный поиск

для всех

. Тогда существует интервал такой, что в методе спуска условия (*) и (**) или (*) и (***) удовлетворяются для любых при
и .
Выбор параметров можно обеспечить многими способами, наиболее современной стратегией является перебор с возвратом
(backtracking technique): при фиксированном значении
начиная со значения уменьшаем его умножением на
до тех пор, пока не выполнится условие (*).
Эта процедура приводится ниже. В качестве входных параметров используются текущее значение вектора , содержащее , имена подпрограмм, вычисляющих значение функции и ее якобиана ,
вектор , содержащий текущее направление поиска, а также значения
, обычно порядка 1.0e-4, и масштабного множителя .
На выходе подпрограмма возвращает , вычисленное при подходящем значении .

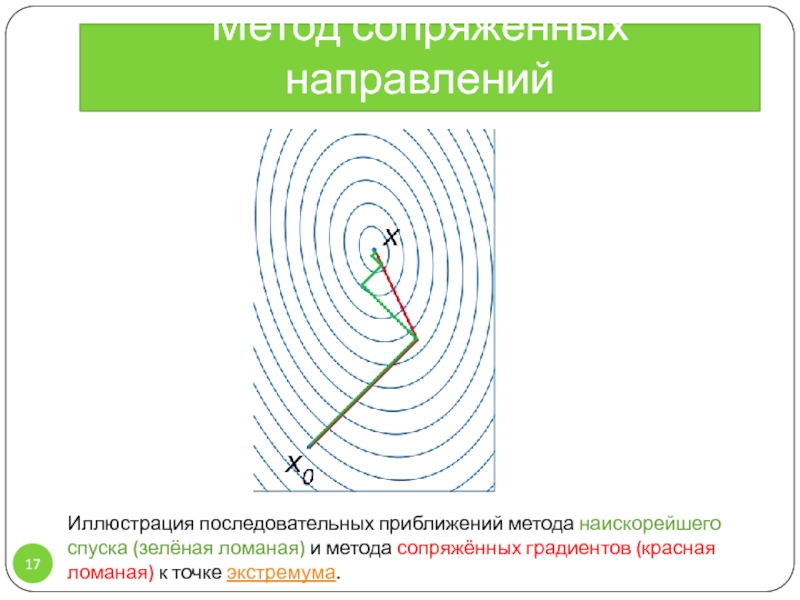
Линейный поиск

которой требуется полный перебор всех возможных вариантов в некотором множестве

М. Как правило позволяет решать задачи, в которых ставятся вопросы типа: «Перечислите все возможные варианты …», «Сколько существует способов …», «Есть ли способ …», «Существует ли объект…» и т. п.
Термин backtrack был введен в 1950 году американским математиком Дерриком Генри Лемером.
Незначительные модификации метода поиска с возвратом, связанные с представлением данных или особенностями реализации, имеют и иные названия: метод ветвей и границ, поиск в глубину, метод проб и ошибок и т. д. Поиск с возвратом практически одновременно и независимо был изобретен многими исследователями еще до его формального описания.

Линейный поиск с возвратом

представляют такие функции, для
которых параметр шага

может быть вычислен точно. Например,
квадратичные функции

где симметричная и положительно определенная матрица и
В этом случае необходимое условие того, что точка минимума функции f(x),
это то, что является решением системы .
В самом деле, легко проверить, что

Как следствие, все итеративные методы решения систем линейных
алгебраических уравнений могут успешно применяться при решении задач
минимизации.

можно определить
оптимальную величину шага

, такую, что функция достигает
минимума вдоль направления спуска.
Приравняем к нулю производную вдоль направления спуска:


откуда следует, что минимум достигается при

-м шаге процесса минимизации

можно вычислить по формуле:

следует, что



Обозначим

, где

положительна. Более того, можно проверить непосредственно, что

; и лишь когда вектор ортогонален , тогда .
Выбор направления спуска в виде приводит к методу
наискорейшего спуска. В этом случае справедливо неравенство


Отсюда следует
Неравенство Канторовича

- симметричная положительно определенная матрица с

наибольшим и наименьшим по модулю значениями соответственно. Тогда для любого ненулевого вектора :

Методы спуска

В том случае, когда A – плохо обусловленная матрица, множитель, определяющий скорость сходимости метода, близок к единице. Отсюда и медленная сходимость метода наискорейшего спуска к точке минимума.
Этот недостаток может быть преодолен за счет выбора A-ортогональных направлений спуска:

квадратичной функции,
основанный на вычислении A-сопряженных направлений спуска, достигает
результата

после самое большое n итераций, если параметр
вычисляется по формуле


Более того, для любого k, x (k+1) является точкой минимума на
подпространстве, натянутом на векторы и

Метод сопряженных направлений

процедурой. Для начального приближения

положим и формулы метода сопряженных градиентов записываются в виде:

Зная число обусловленности матрицы можно оценить скорость сходимости метода:

предобуславливания матрицы с целью уменьшения числа обусловленности.
Замечание. Случай не

квадратичных функций. Метод сопряженных
направлений может быть распространен и на случай не квадратичных
функций. Однако в этом случае оптимальное значение параметра
не может быть определено аналитически и для его отыскания придется
решать одномерную оптимизационную задачу. Мало того, параметры
могут определяться не единственным образом. Наиболее надежны два
варианта выбора :
Флетчера-Ривса (Fletcher-Reeves):

Полака-Рибиера (Polak-Ribiere):

Метод сопряженных направлений

и метода сопряжённых градиентов (красная ломаная) к точке экстремума.

b where A is a real, symmetric, positive-definite matrix. The

input vector x0 can be an approximate initial solution or 0.

Example code in GNU Octave

function [x] = conjgrad(A,b,x)
r=b-A*x;
p=r;
rsold=r'*r;
for i=1:size(A)(1)
Ap=A*p;
alpha=rsold/(p'*Ap);
x=x+alpha*p;
r=r-alpha*Ap;
rsnew=r'*r;
if sqrt(rsnew)<1e-10 break;
end
p=r+rsnew/rsold*p;
rsold=rsnew;
end
end