Разделы презентаций

ЛИНЕЙНАЯ АЛГЕБРА

Содержание

 5. Линейные отображения Рассматриваемые вопросы:5.1. Отображения5.2. Образ, ранг, ядро, дефект отображения5.3. Линейные операторы и их свойства5.4. Структура линейного оператора5.5. Пример нахождения ядра и размера дефекта оператора© Веденяпин Е.Н. 2013

Слайды и текст этой презентации

Слайд 1© Веденяпин Е.Н. 2013
ЛИНЕЙНАЯ АЛГЕБРА
Проф.
ВЕДЕНЯПИН
Евгений Николаевич
Евразийский открытый институт
Кафедра естественнонаучных, математических

и общетехнических дисциплин

© Веденяпин Е.Н. 2013ЛИНЕЙНАЯ АЛГЕБРАПроф.ВЕДЕНЯПИНЕвгений НиколаевичЕвразийский открытый институтКафедра естественнонаучных, математических и общетехнических дисциплин

Слайд 2 5. Линейные отображения
Рассматриваемые вопросы:

5.1. Отображения
5.2. Образ, ранг, ядро, дефект

отображения
5.3. Линейные операторы и их свойства
5.4. Структура линейного оператора
5.5. Пример

нахождения ядра и размера дефекта оператора

© Веденяпин Е.Н. 2013

 5. Линейные отображения Рассматриваемые вопросы:5.1. Отображения5.2. Образ, ранг, ядро, дефект отображения5.3. Линейные операторы и их свойства5.4. Структура

Слайд 35.1. Отображения 
5.1.1. Определение отображения

Пусть


– линейные пространства размерности n и m.

Отображением

линейного пространства Rn1 в линейное пространство Rn2 называется правило

, по которому каждому элементу хRn1 ставится в соответствие единственный элемент уRm2.

Обозначение:

© Веденяпин Е.Н. 2013

5.1. Отображения 5.1.1. Определение отображенияПусть– линейные пространства размерности n и m.Отображением линейного пространства Rn1 в линейное пространство Rn2

Слайд 4© Веденяпин Е.Н. 2013
Частный случай отображения
Частным случаем отображения является функция


поскольку

каждому значению аргумента х по определенному правилу f ставится в

соответствие единственный элемент у.

Пример
© Веденяпин Е.Н. 2013Частный случай отображенияЧастным случаем отображения является функцияпоскольку каждому значению аргумента х по определенному правилу

Слайд 5© Веденяпин Е.Н. 2013
5.1.2. Определение линейного отображения
Отображение называется линейным, если

© Веденяпин Е.Н. 20135.1.2. Определение линейного отображенияОтображение называется линейным, если

Слайд 6© Веденяпин Е.Н. 2013
Пример 1 линейного отображения
Если каждому вектору хRn

трехмерного пространства поставлен в соответствие вектор


то говорят, что задано отображение

подобия.

Процесс отображения представляет собой умножение каждого вектора на число.
© Веденяпин Е.Н. 2013Пример 1 линейного отображенияЕсли каждому вектору хRn трехмерного пространства поставлен в соответствие векторто говорят,

Слайд 7© Веденяпин Е.Н. 2013
Пример 2 линейного отображения
Если каждой матрице-столбцу Х

размерности 1хn из пространства матриц Rnх1 ставится в соответствие матрица-столбец

Y размерности 1хm из пространства матриц Rmх1, то задано отображение пространства столбцов Х размерности 1хn в пространство столбцов Y размерности 1х m.

Процесс отображения представляет собой умножение матрицы Р на столбцы Х
© Веденяпин Е.Н. 2013Пример 2 линейного отображенияЕсли каждой матрице-столбцу Х размерности 1хn из пространства матриц Rnх1 ставится

Слайд 8© Веденяпин Е.Н. 2013
5.1.3. Равные линейные отображения
Равными называются линейные отображения

и , если

© Веденяпин Е.Н. 20135.1.3. Равные линейные отображенияРавными называются линейные отображения и , если

Слайд 95.2. Образ, ранг, ядро, дефект отображения 
5.2.1. Образ и ранг отображения

Образом

im линейного отображения называется множество всех элементов пространства

уRm, для каждого из которых


Рангом линейного отображения называется размерность образа этого отображения.

© Веденяпин Е.Н. 2013

5.2. Образ, ранг, ядро, дефект отображения 5.2.1. Образ и ранг отображенияОбразом im линейного отображения называется множество

Слайд 10© Веденяпин Е.Н. 2013
5.2.2. Ядро и дефект линейного отображения
Ядром ker

линейного отображения называется множество всех элементов пространства хRn1,

каждый из которых переводится отображением в нулевой элемент у=0 пространства Rm2.

Дефектом def линейного отображения называется размерность ядра этого отображения.
© Веденяпин Е.Н. 20135.2.2. Ядро и дефект линейного отображенияЯдром ker линейного отображения называется множество всех

Слайд 11© Веденяпин Е.Н. 2013
5.2.3. Теорема об образе и ядре отображения
Образ

и ядро линейного отображения являются подпространствами соответственно Rm2 и

Rn1.

Доказательство

1. Пусть у1 и у2 – элементы образа линейного пространства.

Тогда найдутся такие элементы х1 и х2 из Rn1, что


Найдем линейную комбинацию
© Веденяпин Е.Н. 20135.2.3. Теорема об образе и ядре отображенияОбраз и ядро линейного отображения являются подпространствами

Слайд 12© Веденяпин Е.Н. 2013
Доказательство (продолжение)
Из равенства


следует, что для элемента


нашелся элемент


Следовательно, произвольная

линейная комбинация


также лежит в im , то есть образ

линейного отображения является линейным подпространством пространства Rm2.
© Веденяпин Е.Н. 2013Доказательство (продолжение)Из равенстваследует, что для элементанашелся элементСледовательно, произвольная линейная комбинациятакже лежит в im

Слайд 13© Веденяпин Е.Н. 2013
Доказательство (окончание)
2. Пусть теперь х1 и х2 –

элементы ядра линейного преобразования .

Тогда

Составим линейную комбинацию


Следовательно, отображение переводит

линейную комбинацию переводит линейную комбинацию


в нулевой элемент у=0.

Значит, ядро линейного отображения является линейным подпространством.
© Веденяпин Е.Н. 2013Доказательство (окончание)2. Пусть теперь х1 и х2 – элементы ядра линейного преобразования .ТогдаСоставим

Слайд 14© Веденяпин Е.Н. 2013
5.2.4. Теорема об отображении базиса
Пусть

является произвольным базисом

пространства Rn1.

Тогда, каким бы ни был набор элементов


линейного пространства Rn2,

существует отображение , переводящее векторы еiRn1 в векторы аiRn2, где i=1, 2, 3, …, n.

Это отображение линейно и является единственным.
© Веденяпин Е.Н. 20135.2.4. Теорема об отображении базисаПустьявляется произвольным базисом пространства Rn1.Тогда, каким бы ни был набор

Слайд 15© Веденяпин Е.Н. 2013
5.2.5. Следствие из теоремы об отображении базиса
Линейное

отображение из пространства Rn1 в пространство Rn2 может быть определено

преобразованием базисных векторов (то есть действием линейного отображения на векторы базиса).

Доказательство

Если задать линейное отображение системой уравнений







то действие линейного отображения на произвольный элемент х, разложенный по базису е, будет существовать.
© Веденяпин Е.Н. 20135.2.5. Следствие из теоремы об отображении базисаЛинейное отображение из пространства Rn1 в пространство Rn2

Слайд 165.3. Линейные операторы и их свойства  
5.3.1. Определение линейного оператора

Рассмотрим

линейное отображение, действующее из векторного пространства Rn в это же

векторное пространство Rn. Такое отображение называется линейным оператором.

© Веденяпин Е.Н. 2013

5.3. Линейные операторы и их свойства  5.3.1. Определение линейного оператораРассмотрим линейное отображение, действующее из векторного пространства Rn

Слайд 17© Веденяпин Е.Н. 2013
5.3.2. Арифметические операции с линейными операторами
Введем арифметические

операции с линейными операторами.

Суммой операторов и называется оператор

, который действует по правилу


Произведением оператора на число  называется оператор , который действует по правилу


Произведением оператора на оператор называется, аааааааа, который действует по правилу
© Веденяпин Е.Н. 20135.3.2. Арифметические операции с линейными операторамиВведем арифметические операции с линейными операторами.Суммой операторов и

Слайд 18© Веденяпин Е.Н. 2013
Единичный оператор
Оператор называется единичным, если

© Веденяпин Е.Н. 2013Единичный операторОператор называется единичным, если

Слайд 19© Веденяпин Е.Н. 2013
Линейность введенных операторов
Сумма линейных операторов, произведение линейного

оператора на число и произведение линейных операторов в свою очередь

являются линейными операторами.

Докажем, например, что произведение операторов является линейным оператором
© Веденяпин Е.Н. 2013Линейность введенных операторовСумма линейных операторов, произведение линейного оператора на число и произведение линейных операторов

Слайд 205.4. Структура линейного оператора 
5.4.1. Матрица линейного оператора

Пусть в пространстве Rn

задан базис


Разложим произвольный вектор х по этому базису


Подействуем на вектор

х оператором :

© Веденяпин Е.Н. 2013

5.4. Структура линейного оператора 5.4.1. Матрица линейного оператораПусть в пространстве Rn задан базисРазложим произвольный вектор х по этому

Слайд 21© Веденяпин Е.Н. 2013
Разложение оператора по базису
Величины


являются векторами из Rn

и поэтому могут быть разложены по базису


То есть

© Веденяпин Е.Н. 2013Разложение оператора по базисуВеличиныявляются векторами из Rn и поэтому могут быть разложены по базисуТо

Слайд 22© Веденяпин Е.Н. 2013
Разложение оператора по базису (продолжение)
Тогда







С другой стороны,

есть некоторый вектор уRn, который может быть разложен

по заданному базису
© Веденяпин Е.Н. 2013Разложение оператора по базису (продолжение)ТогдаС другой стороны, есть некоторый вектор уRn,

Слайд 23© Веденяпин Е.Н. 2013
Единственность разложения оператора по базису
В силу единственности

разложения вектора у по базису получаем систему уравнений

© Веденяпин Е.Н. 2013Единственность разложения оператора по базисуВ силу единственности разложения вектора у по базису получаем систему

Слайд 24© Веденяпин Е.Н. 2013
Матричная форма системы уравнений
Развернутая матричная форма системы

уравнений








Сокращенная матричная форма системы уравнений

© Веденяпин Е.Н. 2013Матричная форма системы уравненийРазвернутая матричная форма системы уравненийСокращенная матричная форма системы уравнений

Слайд 25© Веденяпин Е.Н. 2013
Матрица линейного оператора
Таким образом, действие линейного оператора

на вектор х сводится к умножению некоторой матрицы


на вектор-столбец

х, составленный из координат вектора х в базисе е.

Матрица Р называется матрицей линейного оператора в базисе
© Веденяпин Е.Н. 2013Матрица линейного оператораТаким образом, действие линейного оператора на вектор х сводится к умножению

Слайд 26© Веденяпин Е.Н. 2013
5.4.2. Ранг линейного оператора
Исследуем ранг линейного оператора

.

Оператор , является частным случаем линейного

отображения.

Следовательно, ранг оператора равен размерности образа а этого отображения, а, следовательно, размерности соответствующего подпространства.
© Веденяпин Е.Н. 20135.4.2. Ранг линейного оператораИсследуем ранг линейного оператора .Оператор , является

Слайд 27© Веденяпин Е.Н. 2013
Размерность подпространства
Подпространство составлено из векторов


и их линейных

комбинаций.

Число линейно независимых векторов среди них равно размерности подпространства.

Координаты векторов


образуют

столбцы матрицы оператора .
© Веденяпин Е.Н. 2013Размерность подпространстваПодпространство составлено из векторови их линейных комбинаций.Число линейно независимых векторов среди них равно

Слайд 28© Веденяпин Е.Н. 2013
Ранг матрицы оператора и ранг оператора
Число линейно

независимых столбцов матрицы Р (им соответствуют линейно независимые векторы) и

есть ранг линейного оператора .

ВЫВОД. Ранг матрицы Р линейного оператора равен рангу оператора.
© Веденяпин Е.Н. 2013Ранг матрицы оператора и ранг оператораЧисло линейно независимых столбцов матрицы Р (им соответствуют линейно

Слайд 29© Веденяпин Е.Н. 2013
Случай невырожденной матрицы оператора
Если ранг линейного оператора

равен n (r=n, то есть матрица оператора не вырождена (|P|0),

только нулевой вектор преобразуется оператором в нулевой вектор.

Действительно, матричное уравнение


имеет единственное решение, что обеспечивает взаимно однозначное соответствие между векторами х и у, причем нулевому вектору соответствует нулевой вектор.
© Веденяпин Е.Н. 2013Случай невырожденной матрицы оператораЕсли ранг линейного оператора равен n (r=n, то есть матрица оператора

Слайд 30© Веденяпин Е.Н. 2013
Случай вырожденной матрицы оператора
Если матрица линейного оператора

является вырожденной (r

оператор переводит в нулевые векторы и возникает дефект линейного оператора.

Соответствующее подпространство ядра оператора перестает быть нулевым.
© Веденяпин Е.Н. 2013Случай вырожденной матрицы оператораЕсли матрица линейного оператора является вырожденной (r

Слайд 31© Веденяпин Е.Н. 2013
5.5. Пример нахождения ядра и размера дефекта

оператора
5.5.1. Постановка задачи

Линейный оператор задан матрицей





Найти базис ядра и размер

дефекта оператора.
© Веденяпин Е.Н. 20135.5. Пример нахождения ядра и размера дефекта оператора5.5.1. Постановка задачиЛинейный оператор задан матрицейНайти базис

Слайд 32© Веденяпин Е.Н. 2013
5.5.2. Матричная запись системы уравнений
Пусть вектор




принадлежит ядру

линейного оператора , то есть оператор переводит вектор х в

нулевой вектор


Развернутое матричное уравнение
© Веденяпин Е.Н. 20135.5.2. Матричная запись системы уравненийПусть векторпринадлежит ядру линейного оператора , то есть оператор переводит

Слайд 33© Веденяпин Е.Н. 2013
5.5.3. Решение системы уравнений
Приведем матрицу системы к

ступенчатому виду





Решение системы уравнений

© Веденяпин Е.Н. 20135.5.3. Решение системы уравненийПриведем матрицу системы к ступенчатому видуРешение системы уравнений

Слайд 34© Веденяпин Е.Н. 2013
5.5.4. Нахождение ядра и дефекта оператора
Совокупность векторов

х составляет подпространство решений уравнения


а, следовательно, ядро оператора .

Базисом

подпространства (ядра оператора) можно выбрать вектор






Размерность подпространства (размер дефекта) равны единице.
© Веденяпин Е.Н. 20135.5.4. Нахождение ядра и дефекта оператораСовокупность векторов х составляет подпространство решений уравненияа, следовательно, ядро

Слайд 35Пусть

– базис исходного пространства R3, в котором задана матрица оператора

.

Образ является линейным подпространством,

построенным на векторах


То есть данное линейное подпространство является линейной оболочкой, натянутой на вектора

© Веденяпин Е.Н. 2013

5.5.5. Обсуждение полученных результатов

Пусть– базис исходного пространства R3, в котором задана матрица оператора . Образ

Слайд 36Тогда





Ранг матрицы коэффициентов полученной системы уравнений





равен 2.
© Веденяпин Е.Н. 2013
Обсуждение

полученных результатов (продолжение)

ТогдаРанг матрицы коэффициентов полученной системы уравненийравен 2.© Веденяпин Е.Н. 2013Обсуждение полученных результатов (продолжение)

Слайд 37Следовательно, только два вектора из трех


являются линейно независимыми, например,


Значит, базис

образа оператора состоит из

2 векторов..

ВЫВОД. Оператор , имея дефект, равный 1, переводит векторы из пространства R3 (dim R=3) в подпространство R2 (dim R=2).

Замечание. Для любого линейного отображения справедлива формула

© Веденяпин Е.Н. 2013

Обсуждение полученных результатов (окончание)

Следовательно, только два вектора из трехявляются линейно независимыми, например,Значит, базис образа оператора

Слайд 38 6. Собственные вектора и собственные числа оператора
Рассматриваемые вопросы:

6.1. Изменение

матрицы оператора при переходе к новому базису
6.2. Характеристический многочлен и

характеристическое уравнение
6.3. Теорема Гамильтона-Кэли
6.4. Собственный вектор и собственное число оператора

© Веденяпин Е.Н. 2013

 6. Собственные вектора и собственные числа оператора Рассматриваемые вопросы:6.1. Изменение матрицы оператора при переходе к новому базису6.2.

Слайд 396.1. Изменение матрицы оператора при переходе к новому базису 
6.1.1. Связь

между координатами векторов в разных базисах

Пусть в пространстве Rn

заданы два базиса


Связь между базисами задается невырожденной матрицей перехода


Пусть имеются два вектора хRn, уRn.

Связь между координатами векторов в старом и новом базисах

© Веденяпин Е.Н. 2013

6.1. Изменение матрицы оператора при переходе к новому базису 6.1.1. Связь между координатами векторов в разных базисах Пусть

Слайд 40© Веденяпин Е.Н. 2013
Переход к новому базису
Пусть задан оператор линейного

преобразования .

Матрица оператора в старом базисе будет Р.

Пусть

у –это образ х. В старом базисе


Тогда в новом базисе


Выразим у’ через x’
© Веденяпин Е.Н. 2013Переход к новому базисуПусть задан оператор линейного преобразования .Матрица оператора в старом

Слайд 41© Веденяпин Е.Н. 2013
Преобразующая матрица
Обозначим матрицу оператора в

новом базисе через


Получим


Матрица А’ называется преобразующей матрицей.

Замечание. Матрицы А и

А’ описывают действие одного и того же оператора в разных базисах.
© Веденяпин Е.Н. 2013Преобразующая матрицаОбозначим матрицу оператора в новом базисе черезПолучимМатрица А’ называется преобразующей матрицей.Замечание.

Слайд 42© Веденяпин Е.Н. 2013
6.1.2. Подобие матриц линейного оператора
Матрицы А и

А’ подобны, то есть


Действительно,



ВЫВОД. Определитель матрицы линейного оператора

не зависит от выбора базиса в пространстве Rn.
© Веденяпин Е.Н. 20136.1.2. Подобие матриц линейного оператораМатрицы А и А’ подобны, то естьДействительно,ВЫВОД. Определитель матрицы линейного

Слайд 43© Веденяпин Е.Н. 2013
6.1.3. Примеры линейных операторов
Пример 1. Если

то оператор

является линейным и называется нулевым оператором .

Поскольку

для любого базиса


то матрицей нулевого оператора является нулевая матрица
© Веденяпин Е.Н. 20136.1.3. Примеры линейных операторовПример 1. Еслито оператор является линейным и называется нулевым

Слайд 44© Веденяпин Е.Н. 2013
Пример 2 линейного оператора
Если для каждого вектора

хRn


то оператор является линейным и называется тождественным оператором .



Матрицей тождественного оператора является единичная матрица
© Веденяпин Е.Н. 2013Пример 2 линейного оператораЕсли для каждого вектора хRnто оператор является линейным и называется тождественным

Слайд 456.2. Характеристический многочлен и характеристическое уравнение 
6.2.1. Характеристический многочлен

Рассмотрим квадратную

матрицу






Как было показано (п. 8.1.2), все матрицы, подобные матрице А,

то есть все матрицы вида

где С – любая квадратная невырожденная матрица порядка n, имеют одинаковые определители.

© Веденяпин Е.Н. 2013

6.2. Характеристический многочлен и характеристическое уравнение 6.2.1. Характеристический многочлен Рассмотрим квадратную матрицуКак было показано (п. 8.1.2), все матрицы,

Слайд 46© Веденяпин Е.Н. 2013
Характеристический многочлен
Наряду с матрицей А рассмотрим матрицу







Определитель

этой матрицы


представляет собой многочлен степени n относительно .

Многочлен () называется

характеристическим многочленом матрицы А.
© Веденяпин Е.Н. 2013Характеристический многочленНаряду с матрицей А рассмотрим матрицуОпределитель этой матрицыпредставляет собой многочлен степени n относительно

Слайд 47© Веденяпин Е.Н. 2013
6.2.2. Характеристические многочлены подобных матриц
Все подобные матрицы

имеют один и тот же характеристический многочлен, то есть


где


Действительно,

© Веденяпин Е.Н. 20136.2.2. Характеристические многочлены подобных матрицВсе подобные матрицы имеют один и тот же характеристический многочлен,

Слайд 48© Веденяпин Е.Н. 2013
6.2.2. Характеристическое уравнение и характеристические числа
Алгебраическое уравнение

степени n относительно 


называется характеристическим уравнением матрицы А.

Корни характеристического уравнения

называются характеристическими числами (собственными значениями).
© Веденяпин Е.Н. 20136.2.2. Характеристическое уравнение и характеристические числаАлгебраическое уравнение степени n относительно называется характеристическим уравнением матрицы

Слайд 49© Веденяпин Е.Н. 2013
Общий вид характеристического уравнения
Характеристическое уравнение имеет вид




Здесь

k – след k-ого порядка матрицы А.

© Веденяпин Е.Н. 2013Общий вид характеристического уравненияХарактеристическое уравнение имеет видЗдесь k – след k-ого порядка матрицы А.

Слайд 50© Веденяпин Е.Н. 2013
След k-ого порядка матрицы
След k-ого порядка матрицы

А – это сумма всевозможных главных миноров k-ого порядка








Замечание. Для

каждого k существует



главных миноров.
© Веденяпин Е.Н. 2013След k-ого порядка матрицыСлед k-ого порядка матрицы А – это сумма всевозможных главных миноров

Слайд 51© Веденяпин Е.Н. 2013
6.2.3. Число корней характеристического уравнения
Характеристическое уравнение имеет

n корней (с учетом кратности).


Сумма корней характеристического многочлена равна следу

первого порядка матрицы А



Произведение корней характеристического многочлена равно следу n-го порядка матрицы А (то есть ее определителю)
© Веденяпин Е.Н. 20136.2.3. Число корней характеристического уравненияХарактеристическое уравнение имеет n корней (с учетом кратности).Сумма корней характеристического

Слайд 52© Веденяпин Е.Н. 2013
6.2.4. Метод Фаддеева для нахождения коэффициентов k
Одним

из методов вычисления коэффициентов k (k=1, 2, …, n) характеристического

уравнения является метод Фаддеева.

Пусть оператор задан матрицей А. Тогда схема вычисления коэффициентов имеет вид
© Веденяпин Е.Н. 20136.2.4. Метод Фаддеева для нахождения коэффициентов kОдним из методов вычисления коэффициентов k (k=1, 2,

Слайд 53© Веденяпин Е.Н. 2013
6.2.5. Пример нахождения собственных значений
Найти собственные значения

линейного оператора , заданного матрицей






Характеристическое уравнение имеет вид



Найдем коэффициенты

k с помощью метода Фаддеева.
© Веденяпин Е.Н. 20136.2.5. Пример нахождения собственных значенийНайти собственные значения линейного оператора , заданного матрицейХарактеристическое уравнение

Слайд 54© Веденяпин Е.Н. 2013
Вычисление коэффициентов методом Фаддеева

© Веденяпин Е.Н. 2013Вычисление коэффициентов методом Фаддеева

Слайд 55© Веденяпин Е.Н. 2013
Решение характеристического уравнения
Получили характеристическое уравнение



Преобразуем к виду



Собственные

числа линейного оператора

© Веденяпин Е.Н. 2013Решение характеристического уравненияПолучили характеристическое уравнениеПреобразуем к видуСобственные числа линейного оператора

Слайд 566.3. Теорема Гамильтона-Кэли 
6.3.1. Формулировка теоремы Гамильтона - Кэли

Каждая квадратная матрица

является корнем своего характеристического многочлена.
© Веденяпин Е.Н. 2013

6.3. Теорема Гамильтона-Кэли 6.3.1. Формулировка теоремы Гамильтона - КэлиКаждая квадратная матрица является корнем своего характеристического многочлена.© Веденяпин Е.Н.

Слайд 57© Веденяпин Е.Н. 2013
Гамильтон и Кэли
Уильям Роуэн ГАМИЛЬТОН
(1805 – 1865)
Артур


КЭЛИ
(1821 – 1895)

© Веденяпин Е.Н. 2013Гамильтон и КэлиУильям Роуэн ГАМИЛЬТОН(1805 – 1865)Артур КЭЛИ(1821 – 1895)

Слайд 58© Веденяпин Е.Н. 2013
6.3.2. Пример
Линейный оператор задан матрицей




Найти

характеристический многочлен () и показать, что он равен нулю.


Составим матрицу

© Веденяпин Е.Н. 20136.3.2. ПримерЛинейный оператор задан матрицейНайти характеристический многочлен () и показать, что он

Слайд 59© Веденяпин Е.Н. 2013
Пример (окончание)
Характеристический многочлен имеет вид




Тогда в соответствии с

теоремой Гамильтона-Кэли

© Веденяпин Е.Н. 2013Пример (окончание)Характеристический многочлен имеет видТогда в соответствии с теоремой Гамильтона-Кэли

Слайд 606.4. Собственный вектор и собственное число оператора
6.4.1. Определение собственного вектора

линейного оператора

Пусть в пространстве Rn задан линейный оператор .

Ненулевой

вектор хRn, удовлетворяющий условию


называется собственным вектором оператора , а соответствующее число  называется собственным значением оператора .

Замечание. Образом собственного вектора х является коллинеарный ему вектор х.

© Веденяпин Е.Н. 2013

6.4. Собственный вектор и собственное число оператора6.4.1. Определение собственного вектора линейного оператораПусть в пространстве Rn задан линейный

Слайд 61© Веденяпин Е.Н. 2013
6.4.2. Первое свойство собственных векторов
Каждому собственному вектору

соответствует единственное собственное значение.

Действительно, предположим противное: пусть собственному вектору х

соответствуют два собственных значения 1 и 2.

Тогда


Отсюда


Поскольку по условию х0, то 1=2.
© Веденяпин Е.Н. 20136.4.2. Первое свойство собственных векторовКаждому собственному вектору соответствует единственное собственное значение.Действительно, предположим противное: пусть

Слайд 62© Веденяпин Е.Н. 2013
6.4.3. Второе свойство собственных векторов
Если х1 и

х2 – собственные векторы оператора с одним и тем

же собственным значением , то их сумма х1+х2 также является собственным вектором оператора с тем же собственным значением .

Действительно, так как


то
© Веденяпин Е.Н. 20136.4.3. Второе свойство собственных векторовЕсли х1 и х2 – собственные векторы оператора с

Слайд 63© Веденяпин Е.Н. 2013
6.4.3. Третье свойство собственных векторов
Если х –

собственный вектор оператора с собственным значением , любой вектор

х также является собственным вектором оператора ы с тем же собственным значением .

Действительно,



ВЫВОД 1. Каждому собственному значению  соответствует бесчисленное множество коллинеарных собственных векторов.

ВЫВОД 2. Из свойств 2 и 3 следует, что множество собственных векторов линейного оператора , соответствующих одному и тому же собственному значению, образует пространство, являющееся подпространством пространства Rn.
© Веденяпин Е.Н. 20136.4.3. Третье свойство собственных векторовЕсли х – собственный вектор оператора с собственным значением

Слайд 64© Веденяпин Е.Н. 2013
6.4.4. Теорема о существовании собственных векторов
В комплексном

линейном пространстве Rn каждый линейный оператор имеет, по

крайней мере, один собственный вектор.

Доказательство

Пусть – линейный оператор, заданный в пространстве Rn, а х – собственный вектор этого оператора с собственным значением .

Выберем произвольный базис


и обозначим координаты вектора х через (х1, х2, …, хn).
© Веденяпин Е.Н. 20136.4.4. Теорема о существовании собственных векторовВ комплексном линейном пространстве Rn каждый линейный оператор

Слайд 65© Веденяпин Е.Н. 2013
Доказательство (продолжение)
Если А – матрица оператора

в базисе


то в матричной форме получаем

или


В координатной форме

© Веденяпин Е.Н. 2013Доказательство (продолжение)Если А – матрица оператора в базисето в матричной форме получаемилиВ

Слайд 66© Веденяпин Е.Н. 2013
Доказательство (окончание)
Для отыскания собственного вектора необходимо найти нетривиальное

решение полученной системы уравнений.

Нетривиальное решение существует тогда и только тогда,

когда определитель системы уравнений равен нулю, то есть


Следовательно, собственное значение оператора является его характеристическим числом, которое всегда существует.

Подставляя это число в систему уравнений, находим нетривиальное решение , которое определяет искомый собственный вектор.
© Веденяпин Е.Н. 2013Доказательство (окончание)Для отыскания собственного вектора необходимо найти нетривиальное решение полученной системы уравнений.Нетривиальное решение существует

Слайд 67© Веденяпин Е.Н. 2013
6.4.5. Пример нахождения собственных векторов
Найти собственные векторы

линейного оператора , заданного матрицей






Составим характеристическое уравнение

© Веденяпин Е.Н. 20136.4.5. Пример нахождения собственных векторовНайти собственные векторы линейного оператора , заданного матрицейСоставим характеристическое

Слайд 68© Веденяпин Е.Н. 2013
Пример (продолжение)
Раскрывая определитель, получаем


Корни характеристического уравнения (собственные значения)


Для

нахождения собственных векторов оператора подставим найденные корни в систему

уравнений
© Веденяпин Е.Н. 2013Пример (продолжение)Раскрывая определитель, получаемКорни характеристического уравнения (собственные значения)Для нахождения собственных векторов оператора подставим

Слайд 69© Веденяпин Е.Н. 2013
Пример (продолжение)
Подставляя корни 1=2=1, получаем систему уравнений





Ранг матрицы

системы уравнений равен 1.

Получаем однородную систему трех линейных уравнений,

из которых только одно (любое) линейно независимое.

Общее решение системы
© Веденяпин Е.Н. 2013Пример (продолжение)Подставляя корни 1=2=1, получаем систему уравненийРанг матрицы системы уравнений равен 1. Получаем однородную

Слайд 70© Веденяпин Е.Н. 2013
Пример (продолжение)
Найдем два линейно независимых решения






Собственные векторы, соответствующие

собственным значениям 1=2=1, имеют вид

© Веденяпин Е.Н. 2013Пример (продолжение)Найдем два линейно независимых решенияСобственные векторы, соответствующие собственным значениям 1=2=1, имеют вид

Слайд 71© Веденяпин Е.Н. 2013
Пример (продолжение)
При 3=4 имеем




Ранг матрицы системы равен 2.

Получаем

однородную систему трех линейных уравнений, из которых два линейно независимые.

Общее

решение системы уравнений
© Веденяпин Е.Н. 2013Пример (продолжение)При 3=4 имеемРанг матрицы системы равен 2.Получаем однородную систему трех линейных уравнений, из

Слайд 72© Веденяпин Е.Н. 2013
Пример (окончание)
Собственный вектор, соответствующий собственному значению 3=4, равен

© Веденяпин Е.Н. 2013Пример (окончание)Собственный вектор, соответствующий собственному значению 3=4, равен

Слайд 73© Веденяпин Е.Н. 2013
6.4.6. Теорема о линейно независимых собственных векторах
Пусть

собственные значения 1, 2, 3, …, n линейного оператора яя

попарно различны.

Тогда соответствующие им собственные векторы



линейно независимы.
© Веденяпин Е.Н. 20136.4.6. Теорема о линейно независимых собственных векторахПусть собственные значения 1, 2, 3, …, n

Слайд 74© Веденяпин Е.Н. 2013
Следствие
Если все собственные значения 1, 2, 3,

…, n линейного оператора яя попарно различны, то соответствующие им

собственные векторы образуют базис в пространстве Rn.
© Веденяпин Е.Н. 2013СледствиеЕсли все собственные значения 1, 2, 3, …, n линейного оператора яя попарно различны,

Слайд 75© Веденяпин Е.Н. 2013
6.4.7. Теорема о базисе, составленном из линейно

независимых собственных векторах
Если в качестве базиса пространства Rn выбрать n

линейно независимых собственных векторов, то оператору в этом базисе соответствует диагональная матрица
© Веденяпин Е.Н. 20136.4.7. Теорема о базисе, составленном из линейно независимых собственных векторахЕсли в качестве базиса пространства

Слайд 76© Веденяпин Е.Н. 2013
Оператор простой структуры
Линейный оператор яя в пространстве

Rn. называется оператором простой структуры, если он имеет n линейно

независимых собственных векторов.

Операторы простой структуры, и только они, имеют диагональные матрицы в некотором базисе.

Этот базис может быть составлен лишь из собственных векторов оператора .

Действие любого оператора простой структуры всегда сводится к растяжению (сжатию) координат вектора в данном базисе.
© Веденяпин Е.Н. 2013Оператор простой структурыЛинейный оператор яя в пространстве Rn. называется оператором простой структуры, если он

Слайд 77 7. Квадратичные формы
Рассматриваемые вопросы:

7.1. Понятие квадратичной формы
7.2. Линейное преобразование переменных

в квадратичной форме
7.3. Ортогональные преобразования
7.4. Ортогональное преобразование квадратичной формы
7.5. Положительно

определенные квадратичные формы

© Веденяпин Е.Н. 2013

 7. Квадратичные формыРассматриваемые вопросы:7.1. Понятие квадратичной формы7.2. Линейное преобразование переменных в квадратичной форме7.3. Ортогональные преобразования7.4. Ортогональное преобразование

Слайд 787.1. Понятие квадратичной формы 
7.1.1. Определение квадратичной формы

Квадратичной формой от n

неизвестных х1, х2, х3, …, xn называется алгебраическая сумма, каждый

член которой является либо квадратом одного из неизвестных, либо произведением двух различных неизвестных.

Общий вид квадратичной формы

© Веденяпин Е.Н. 2013

7.1. Понятие квадратичной формы 7.1.1. Определение квадратичной формыКвадратичной формой от n неизвестных х1, х2, х3, …, xn называется

Слайд 79© Веденяпин Е.Н. 2013
Матрица квадратичной формы (треугольная форма)
Коэффициенты aij в

данной записи образуют треугольную матрицу









Замечание. Данная форма записи неудобна для

использования, поскольку матрица квадратичной формы несимметрична.
© Веденяпин Е.Н. 2013Матрица квадратичной формы (треугольная форма)Коэффициенты aij в данной записи образуют треугольную матрицуЗамечание. Данная форма

Слайд 80© Веденяпин Е.Н. 2013
7.1.2. Правильная запись квадратичной формы
Запишем квадратичную форму

f(х1, х2, х3, …, xn) в виде






Замечание. Коэффициенты cij матрицы

квадратичной формы в данной записи симметричны (cij= cji).

Такая запись квадратичной формы называется правильной.
© Веденяпин Е.Н. 20137.1.2. Правильная запись квадратичной формыЗапишем квадратичную форму f(х1, х2, х3, …, xn) в видеЗамечание.

Слайд 81© Веденяпин Е.Н. 2013
Матрица квадратичной формы (правильная форма)
Симметричная матрица С

называется матрицей квадратичной формы.

© Веденяпин Е.Н. 2013Матрица квадратичной формы (правильная форма)Симметричная матрица С называется матрицей квадратичной формы.

Слайд 82© Веденяпин Е.Н. 2013
7.1.3. Матричная запись квадратичной формы
Квадратичную форму






можно записать

более компактно, если использовать матричные обозначения

© Веденяпин Е.Н. 20137.1.3. Матричная запись квадратичной формыКвадратичную формуможно записать более компактно, если использовать матричные обозначения

Слайд 83В матричной записи квадратичная форма принимает вид


где




С – симметричная квадратная

матрица порядка n.

Коэффициенты cii (i=1, 2, …, n) – это

коэффициенты при x2i.

Коэффициенты cij (i, j=1, 2, …, n; ij) – это коэффициенты, равные половине коэффициентов при xixj.

© Веденяпин Е.Н. 2013

Матричная запись

В матричной записи квадратичная форма принимает видгдеС – симметричная квадратная матрица порядка n.Коэффициенты cii (i=1, 2, …,

Слайд 84© Веденяпин Е.Н. 2013
7.1.4. Запись квадратичной формы с помощью скалярного

произведения
Квадратичную форму f(х1, х2, х3, …, xn) можно представить также

в виде скалярного произведения векторов.

Введем вектор



Тогда квадратичную форму можно представить в виде скалярного произведения
© Веденяпин Е.Н. 20137.1.4. Запись квадратичной формы с помощью скалярного произведенияКвадратичную форму f(х1, х2, х3, …, xn)

Слайд 85© Веденяпин Е.Н. 2013
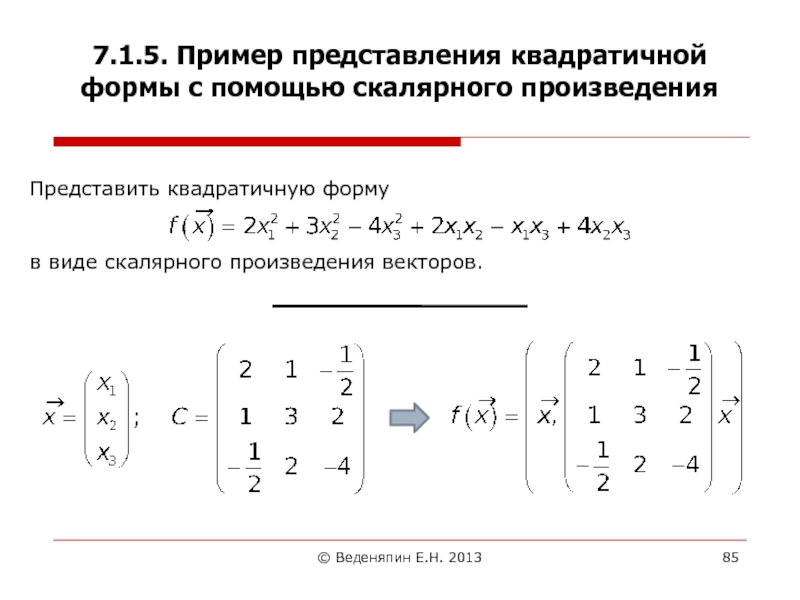
7.1.5. Пример представления квадратичной формы с помощью

скалярного произведения
Представить квадратичную форму


в виде скалярного произведения векторов.

© Веденяпин Е.Н. 20137.1.5. Пример представления квадратичной формы с помощью скалярного произведенияПредставить квадратичную формув виде скалярного произведения

Слайд 867.2. Линейное преобразование переменных в квадратичной форме 
7.2.1. Линейное преобразование переменных

Пусть

в квадратичной форме


выполнено линейное преобразование переменных х1, х2, х3, …,

xn



с матрицей

© Веденяпин Е.Н. 2013

7.2. Линейное преобразование переменных в квадратичной форме 7.2.1. Линейное преобразование переменныхПусть в квадратичной формевыполнено линейное преобразование переменных х1,

Слайд 87В результате получена квадратичная форма f(у1, у2, у3, …, уn),

зависящая от новых переменных



Квадратичная форма f(у1, у2, у3, …, уn

) имеет правильную запись.

Действительно,



Следовательно, матрица ВТСВ симметрична, а, значит, симметрична и квадратичная форма f(у1, у2, у3, …, уn ), то есть она имеет правильную запись.

© Веденяпин Е.Н. 2013

Линейное преобразование переменных (окончание)

В результате получена квадратичная форма f(у1, у2, у3, …, уn), зависящая от новых переменныхКвадратичная форма f(у1, у2,

Слайд 88© Веденяпин Е.Н. 2013
7.2.2. Пример преобразования переменных квадратичной формы
Осуществить над

квадратичной формой


линейное преобразование, заданное матрицей





Переменные х1, х2, …, хn преобразуются

в переменные у1, у2, …, уn.

Связь между переменными выражается уравнением
© Веденяпин Е.Н. 20137.2.2. Пример преобразования переменных квадратичной формыОсуществить над квадратичной формойлинейное преобразование, заданное матрицейПеременные х1, х2,

Слайд 89© Веденяпин Е.Н. 2013
Пример преобразования переменных (окончание)
Переменные х1, х2, …,

хn преобразуются в переменные у1, у2, …, уn.

Связь между переменными

выражается уравнением



Отсюда


В квадратичной форме вместо переменных х1 и х2 подставляем их выражение через переменные у1 и у2. Получаем
© Веденяпин Е.Н. 2013Пример преобразования переменных (окончание)Переменные х1, х2, …, хn преобразуются в переменные у1, у2,

Слайд 90© Веденяпин Е.Н. 2013
7.2.3. Канонический вид квадратичной формы
Квадратичная форма имеет

канонический вид, если матрица С диагональна.

Замечание. Квадратичная форма в

каноническом виде содержит только квадраты переменных
© Веденяпин Е.Н. 20137.2.3. Канонический вид квадратичной формыКвадратичная форма имеет канонический вид, если матрица С диагональна. Замечание.

Слайд 91© Веденяпин Е.Н. 2013
7.2.4. Нормальный вид квадратичной формы
Нормальным видом квадратичной

формы называется квадратичная форма в каноническом виде, если коэффициенты при

квадратах переменных равны +1.

Пусть


Положим




Получим
© Веденяпин Е.Н. 20137.2.4. Нормальный вид квадратичной формыНормальным видом квадратичной формы называется квадратичная форма в каноническом виде,

Слайд 92© Веденяпин Е.Н. 2013
7.2.5. Теорема о приведении квадратичной формы к

каноническому виду
Всякая квадратичная форма может быть некоторым невырожденным линейным преобразованием

к каноническому виду
© Веденяпин Е.Н. 20137.2.5. Теорема о приведении квадратичной формы к каноническому видуВсякая квадратичная форма может быть некоторым

Слайд 93© Веденяпин Е.Н. 2013
Пример приведения квадратичной формы к каноническому виду
Привести

квадратичную форму



к каноническому виду.


Коэффициент при х220. Сгруппируем все члены, содержащие

х2
© Веденяпин Е.Н. 2013Пример приведения квадратичной формы к каноническому видуПривести квадратичную формук каноническому виду.Коэффициент при х220. Сгруппируем

Слайд 94© Веденяпин Е.Н. 2013
Пример приведения к каноническому виду (продолжение)
Дополним это выражение

до полного квадрата членами, не содержащими х2, и, чтобы квадратичная

форма не изменилась, вычтем добавленные члены






Введем новую переменную


Тогда
© Веденяпин Е.Н. 2013Пример приведения к каноническому виду (продолжение)Дополним это выражение до полного квадрата членами, не содержащими

Слайд 95© Веденяпин Е.Н. 2013
Пример приведения к каноническому виду (продолжение)
К квадратичной форме

W вновь применим метод выделения полного квадрата. Для этого соберем

члены, содержащие х1:



Дополним это выражение до полного квадрата членами, не содержащими х1, и, чтобы квадратичная форма не изменилась, вычтем добавленные члены
© Веденяпин Е.Н. 2013Пример приведения к каноническому виду (продолжение)К квадратичной форме W вновь применим метод выделения полного

Слайд 96© Веденяпин Е.Н. 2013
Пример приведения к каноническому виду (продолжение)
Положим


Тогда исходная квадратичная

форма f(x) принимает вид



Обозначим


Получаем исходную квадратичную форму в каноническом виде

© Веденяпин Е.Н. 2013Пример приведения к каноническому виду (продолжение)ПоложимТогда исходная квадратичная форма f(x) принимает видОбозначимПолучаем исходную квадратичную

Слайд 97© Веденяпин Е.Н. 2013
Пример приведения к каноническому виду (окончание)
Линейные преобразования переменных






Преобразования

переменных в матричной форме

© Веденяпин Е.Н. 2013Пример приведения к каноническому виду (окончание)Линейные преобразования переменныхПреобразования переменных в матричной форме

Слайд 98© Веденяпин Е.Н. 2013
7.2.6. Ранг квадратичной формы
Ранг квадратичной формы –

это ранг матрицы С квадратичной формы.

Замечание 1. Из теоремы о

приведении квадратичной формы к каноническому виду следует, что для данной симметрической матрицы С существует такая невырожденная матрица В, что


где D – диагональная матрица.

Замечание 2. Приведение квадратичной формы к каноническому виду может осуществляться бесконечным множеством способов. Поэтому матрицы В и D определяются неоднозначно. Однако число ненулевых элементов матрицы D однозначно определено и равно рангу матрицы С.
© Веденяпин Е.Н. 20137.2.6. Ранг квадратичной формыРанг квадратичной формы – это ранг матрицы С квадратичной формы.Замечание 1.

Слайд 997.3. Ортогональные преобразования
7.3.1. Ортогональная матрица

Рассмотрим свойства матрицы перехода от одного

ортонормированного базиса к другому ортонормированному базису в пространстве Еn. Введем

понятие ортогональной матрицы.

Матрица Т с вещественными элементами называется ортогональной, если

то есть

© Веденяпин Е.Н. 2013

7.3. Ортогональные преобразования7.3.1. Ортогональная матрицаРассмотрим свойства матрицы перехода от одного ортонормированного базиса к другому ортонормированному базису в

Слайд 100© Веденяпин Е.Н. 2013
Определитель ортогональной матрицы
Из определения ортогональной матрицы следует,

что ортогональная матрица всегда невырожденная, так как

© Веденяпин Е.Н. 2013Определитель ортогональной матрицыИз определения ортогональной матрицы следует, что ортогональная матрица всегда невырожденная, так как

Слайд 101© Веденяпин Е.Н. 2013
7.3.2. Первое свойство ортогональной матрицы
Матрица, обратная ортогональной,

также является ортогональной.

Доказательство

Пусть Т – ортогональная матрица, то есть


Тогда


то есть


Следовательно,

матрица Т – ортогональная.
© Веденяпин Е.Н. 20137.3.2. Первое свойство ортогональной матрицыМатрица, обратная ортогональной, также является ортогональной.ДоказательствоПусть Т – ортогональная матрица,

Слайд 102© Веденяпин Е.Н. 2013
7.3.3. Второе свойство ортогональной матрицы
Матрица


ортогональна тогда

и только тогда, когда ее элементы удовлетворяют равенству

© Веденяпин Е.Н. 20137.3.3. Второе свойство ортогональной матрицыМатрица ортогональна тогда и только тогда, когда ее элементы удовлетворяют

Слайд 103© Веденяпин Е.Н. 2013
7.3.4. Ортогональное преобразование
Линейное преобразование


с ортогональной матрицей Т

называется ортогональным.

Замечание. Так как определитель ортогональной матрицы


то ортогональное преобразование всегда

является невырожденным.
© Веденяпин Е.Н. 20137.3.4. Ортогональное преобразованиеЛинейное преобразованиес ортогональной матрицей Т называется ортогональным.Замечание. Так как определитель ортогональной матрицыто

Слайд 104© Веденяпин Е.Н. 2013
Теорема об ортогональном преобразовании
Ортогональное преобразование не изменяет

скалярного произведения векторов.

Доказательство

Рассмотрим линейный оператор , соответствующий матрице Т, и

два произвольных вектора хRn и уRn.

Их образы будут


Тогда
© Веденяпин Е.Н. 2013Теорема об ортогональном преобразованииОртогональное преобразование не изменяет скалярного произведения векторов.ДоказательствоРассмотрим линейный оператор , соответствующий

Слайд 105© Веденяпин Е.Н. 2013
7.3.5. Следствия из теоремы об ортогональном преобразовании
Следствие

1. Ортогональное преобразование не меняет норм векторов и углов между

векторами.

Следствие 2. Ортогональное преобразование переводит ортонормированный базис в ортонормированный.

Следствие 3. Матрица Т перехода от одного ортонормированного базиса к другому ортонормированному базису является ортогональной.

Следствие 4. Матрица Т, приводящая симметричную матрицу А к диагональному виду, является ортогональной.
© Веденяпин Е.Н. 20137.3.5. Следствия из теоремы об ортогональном преобразованииСледствие 1. Ортогональное преобразование не меняет норм векторов

Слайд 1067.4. Ортогональное преобразование квадратичной формы
7.4.1. Теорема о приведении действительной квадратичной

формы к главным осям

Всякая действительная квадратичная форма некоторым ортогональным преобразованием

неизвестных может быть приведена к каноническому виду.

© Веденяпин Е.Н. 2013

7.4. Ортогональное преобразование квадратичной формы7.4.1. Теорема о приведении действительной квадратичной формы к главным осямВсякая действительная квадратичная форма

Слайд 107© Веденяпин Е.Н. 2013
Следствие
Ортогональное преобразование, приводящее квадратичную форму к каноническому

виду, определяется неоднозначно.

Однако каково бы ни было ортогональное преобразование,

приводящее к каноническому виду квадратичную форму, коэффициенты этого канонического вида равны собственным числам матрицы С.

Каждое собственное число повторяется столько раз, какова его кратность как корня характеристического уравнения.
© Веденяпин Е.Н. 2013СледствиеОртогональное преобразование, приводящее квадратичную форму к каноническому виду, определяется неоднозначно. Однако каково бы ни

Слайд 108© Веденяпин Е.Н. 2013
7.4.2. Пример приведения квадратичной формы к каноническому

виду
Квадратичную форму


привести к каноническому виду.


Матрица квадратичной формы (правильная запись)

© Веденяпин Е.Н. 20137.4.2. Пример приведения квадратичной формы к каноническому видуКвадратичную формупривести к каноническому виду.Матрица квадратичной формы

Слайд 109© Веденяпин Е.Н. 2013
Пример (продолжение)
Характеристическое уравнение имеет вид







Корни характеристического уравнения


Канонический вид

квадратичной формы

© Веденяпин Е.Н. 2013Пример (продолжение)Характеристическое уравнение имеет видКорни характеристического уравненияКанонический вид квадратичной формы

Слайд 110© Веденяпин Е.Н. 2013
Пример (продолжение)
Найдем ортогональное преобразование, осуществляющее приведение f(x) к

каноническому виду.

Решая уравнение


найдем собственные векторы

© Веденяпин Е.Н. 2013Пример (продолжение)Найдем ортогональное преобразование, осуществляющее приведение f(x) к каноническому виду.Решая уравнениенайдем собственные векторы

Слайд 111© Веденяпин Е.Н. 2013
Пример (продолжение)
Преобразуя данную систему векторов в ортонормированную систему,

получим

© Веденяпин Е.Н. 2013Пример (продолжение)Преобразуя данную систему векторов в ортонормированную систему, получим

Слайд 112© Веденяпин Е.Н. 2013
Пример (продолжение)
Данная система векторов определяет ортогональную матрицу


преобразования переменных


в

переменные


Действительно, Х=ТY, откуда

© Веденяпин Е.Н. 2013Пример (продолжение)Данная система векторов определяет ортогональную матрицупреобразования переменныхв переменныеДействительно, Х=ТY, откуда

Слайд 113© Веденяпин Е.Н. 2013
Пример (окончание)
Получаем ортогональное преобразование

© Веденяпин Е.Н. 2013Пример (окончание)Получаем ортогональное преобразование

Слайд 1147.5. Положительно определенные квадратичные формы
9.5.1. Определение положительно определенной квадратичной формы

Квадратичная

форма называется положительно определенной, если все ее значения при вещественных

значениях переменных, не равных одновременно нулю, положительны.

Очевидно, что квадратичная форма



положительно определена.

© Веденяпин Е.Н. 2013

7.5. Положительно определенные квадратичные формы9.5.1. Определение положительно определенной квадратичной формыКвадратичная форма называется положительно определенной, если все ее

Слайд 115© Веденяпин Е.Н. 2013
Отрицательно определенная квадратичная форма
Квадратичная форма называется отрицательно

определенной, если все ее значения отрицательны, за исключением ненулевого значения

при ненулевых значениях переменных.

Квадратичная форма называется положительно (отрицательно) полуопределенной, если она не принимает отрицательных (положительных) значений.

Квадратичные формы, принимающие как положительные, так и отрицательные значения, называются неопределенными.
© Веденяпин Е.Н. 2013Отрицательно определенная квадратичная формаКвадратичная форма называется отрицательно определенной, если все ее значения отрицательны, за

Слайд 116© Веденяпин Е.Н. 2013
Примеры
Пример 1. При n=1 квадратичная форма


либо положительно

определена (при a11>0), либо отрицательно определена (при a11

формы появляются при n≥2.
© Веденяпин Е.Н. 2013ПримерыПример 1. При n=1 квадратичная формалибо положительно определена (при a11>0), либо отрицательно определена (при

Слайд 117© Веденяпин Е.Н. 2013
7.5.2. Критерий Сильвестра
Для того чтобы квадратичная форма





была

положительно определена, необходимо и достаточно выполнение следующих условий:

© Веденяпин Е.Н. 20137.5.2. Критерий СильвестраДля того чтобы квадратичная формабыла положительно определена, необходимо и достаточно выполнение следующих

Слайд 118© Веденяпин Е.Н. 2013
Джеймс Джозеф СИЛЬВЕСТР
Джеймс Джозеф СИЛЬВЕСТР
(1814 – 1897)

© Веденяпин Е.Н. 2013Джеймс Джозеф СИЛЬВЕСТРДжеймс Джозеф СИЛЬВЕСТР(1814 – 1897)

Слайд 119© Веденяпин Е.Н. 2013
7.5.3. Условие отрицательной определенности квадратичной формы
Для того

чтобы квадратичная форма


была отрицательно определена, необходимо и достаточно чтобы



была положительно

определенной, а значит, чтобы все главные миноры матрицы





были положительны.
© Веденяпин Е.Н. 20137.5.3. Условие отрицательной определенности квадратичной формыДля того чтобы квадратичная формабыла отрицательно определена, необходимо и

Слайд 120© Веденяпин Е.Н. 2013
Условие отрицательной определенности
Это означает, что






ВЫВОД. Знаки главных

миноров матрицы C чередуются, начиная со знака минус.

© Веденяпин Е.Н. 2013Условие отрицательной определенностиЭто означает, чтоВЫВОД. Знаки главных миноров матрицы C чередуются, начиная со знака

Слайд 121© Веденяпин Е.Н. 2013
7.5.4. Примеры проверки положительной определенности
Пример 1. Вычислить,

является ли квадратичная форма



положительно (отрицательно) определенной или неопределенной.


Матрица квадратичной формы

имеет вид
© Веденяпин Е.Н. 20137.5.4. Примеры проверки положительной определенностиПример 1. Вычислить, является ли квадратичная формаположительно (отрицательно) определенной или

Слайд 122© Веденяпин Е.Н. 2013
Пример 1 (окончание)
Вычислим главные миноры матрицы С











ВЫВОД. Квадратичная

форма положительно определена.

© Веденяпин Е.Н. 2013Пример 1 (окончание)Вычислим главные миноры матрицы СВЫВОД. Квадратичная форма положительно определена.

Слайд 123© Веденяпин Е.Н. 2013
Пример 2.
Вычислить, является ли квадратичная форма



положительно (отрицательно)

определенной или неопределенной.


Матрица квадратичной формы имеет вид

© Веденяпин Е.Н. 2013Пример 2.Вычислить, является ли квадратичная формаположительно (отрицательно) определенной или неопределенной.Матрица квадратичной формы имеет вид

Слайд 124© Веденяпин Е.Н. 2013
Пример 2 (окончание)
Вычислим главные миноры матрицы С











ВЫВОД. Квадратичная

форма является неопределенной.

© Веденяпин Е.Н. 2013Пример 2 (окончание)Вычислим главные миноры матрицы СВЫВОД. Квадратичная форма является неопределенной.

Слайд 125© Веденяпин Е.Н. 2013
7.5.5. Теорема об инерции квадратичных форм
Число положительных

и число отрицательных квадратов в нормальном виде, к которому приводится

квадратичная форма невырожденными линейными преобразованиями, не зависит от выбора этих преобразований.
© Веденяпин Е.Н. 20137.5.5. Теорема об инерции квадратичных формЧисло положительных и число отрицательных квадратов в нормальном виде,

Слайд 126© Веденяпин Е.Н. 2013
СПАСИБО ЗА ВНИМАНИЕ!

© Веденяпин Е.Н. 2013СПАСИБО ЗА ВНИМАНИЕ!

Похожие презентации

Особенная часть трудового права Особенная часть трудового права 306
МЕХАНИЧЕСКИЕ ПОВРЕЖДЕНИЯ МЕХАНИЧЕСКИЕ ПОВРЕЖДЕНИЯ 382
Жизнь империи в 1775—1796 годах Жизнь империи в 1775—1796 годах 278
Приемы работы с текстом при подготовке части С в ГИА и ЕГЭ Приемы работы с текстом при подготовке части С в ГИА и ЕГЭ 403
Тема 1. Математическая логика Тема 1. Математическая логика 243
Какие бывают водоёмы? Какие бывают водоёмы? 433
Отчёт о водном туристском походе 1 категории сложности по республике Чувашии, Отчёт о водном туристском походе 1 категории сложности по республике Чувашии, 188
Программы для работы со звуком Программы для работы со звуком 306
Разработка инвестиционной программы развития ООО Погода в доме Автор: студент Разработка инвестиционной программы развития ООО Погода в доме Автор: студент 255
ЗЕМЛИ И КНЯЖЕСТВА УДЕЛЬНОЙ РУСИ ЗЕМЛИ И КНЯЖЕСТВА УДЕЛЬНОЙ РУСИ 218
Психические свойства личности: способности Психические свойства личности: способности 276
Труд - право или обязанность Труд - право или обязанность 245
МАУК МЦБ муниципального района Туймазинский район Городская модельная МАУК МЦБ муниципального района Туймазинский район Городская модельная 229
BTL+03+Gifts BTL+03+Gifts 177
Многие звезды украшали русское небо восемнадцатого столетия. Звездою первой Многие звезды украшали русское небо восемнадцатого столетия. Звездою первой 207
лекция 5.ppt лекция 5.ppt 225
Les cafés parisiens Les cafés parisiens 188
Рождество: история и традиции Рождество: история и традиции 227
Авиационные катастрофы, произошедшие по вине наземных служб, за период Авиационные катастрофы, произошедшие по вине наземных служб, за период 331
Дыхание внешнее, транспорт Дыхание внешнее, транспорт 287

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика