Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические вентили
Содержание
- 1. Логические вентили
- 2. Цели и задачиЗнакомство с основными элементами цифровых
- 3. Базовые логические функцииНЕ (NOT) И (AND)ИЛИ (OR)
- 4. Вентиль «НЕ»Определение: операция НЕ выполняется над одной
- 5. Вентиль «И»Определение: результат операции И, выполняемой над
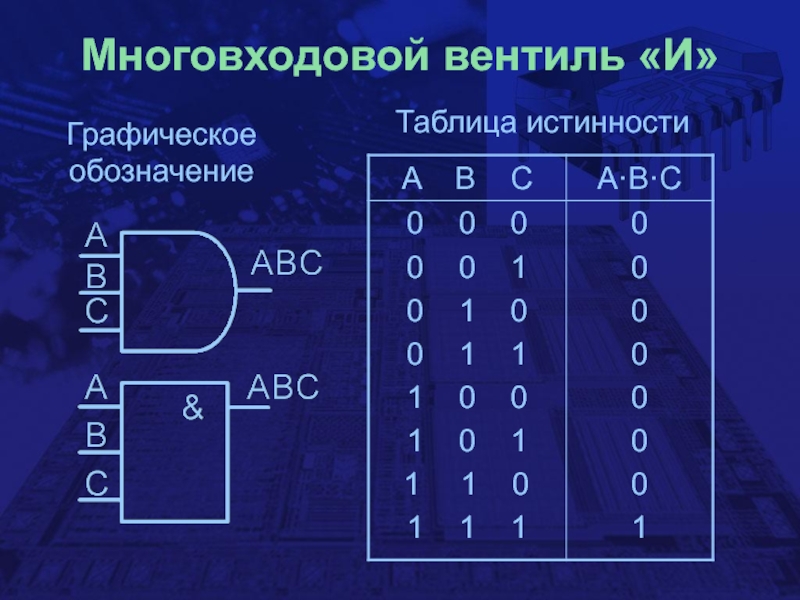
- 6. Многовходовой вентиль «И»Графическое обозначениеТаблица истинности
- 7. Вентиль «ИЛИ»Определение: результат операции ИЛИ, выполняемой над
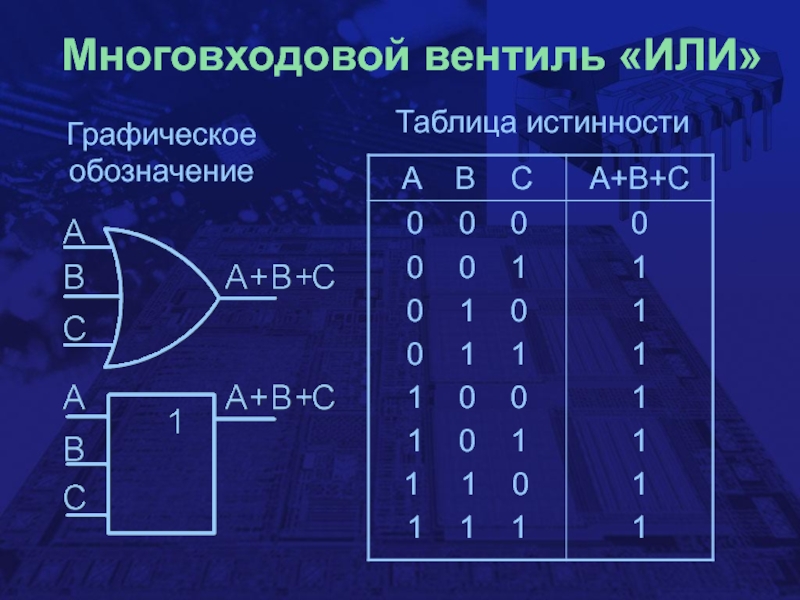
- 8. Многовходовой вентиль «ИЛИ»Графическое обозначениеТаблица истинности
- 9. Упрощенные определенияЕсли хотя бы один из входов
- 10. Булева алгебраРазработана математиком Булем в ХIХ веке.Использовалась
- 11. Основные булевы тождестваA·1 = AA·0 = 0A·A
- 12. Основные булевы тождества для нескольких переменныхA·B·1 =
- 13. Основные правила булевой алгебрыЗакон коммутативности:A · B
- 14. Основные правила булевой алгебрыЗакон дистрибутивности:A (B +
- 15. Положительная и отрицательная логикаКак изменятся таблицы истинности операций «И», «ИЛИ», «НЕ» для положительной и отрицательной логик?
- 16. Дуальные функцииВ положительной логике: f = A
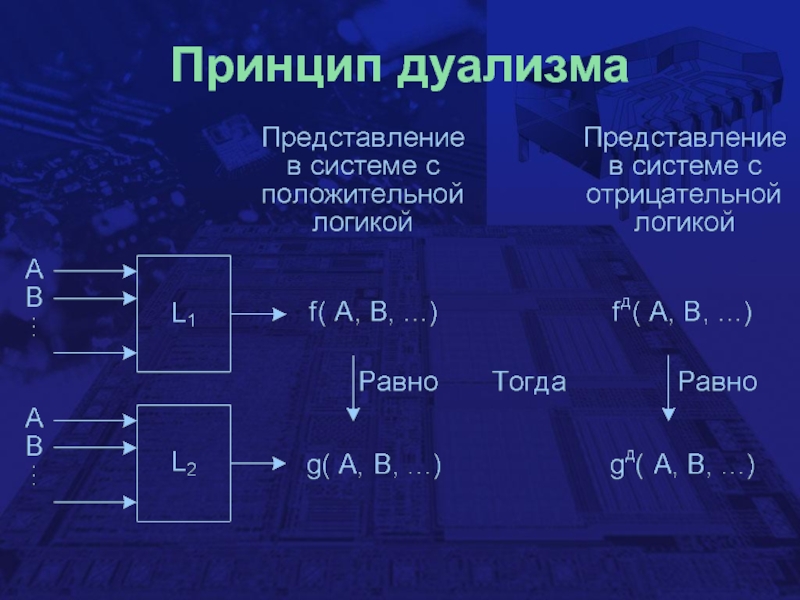
- 17. Принцип дуализмаЕсли есть доказанное равенство:f (A,B,C,…,·,+,0,1) =
- 18. Принцип дуализма
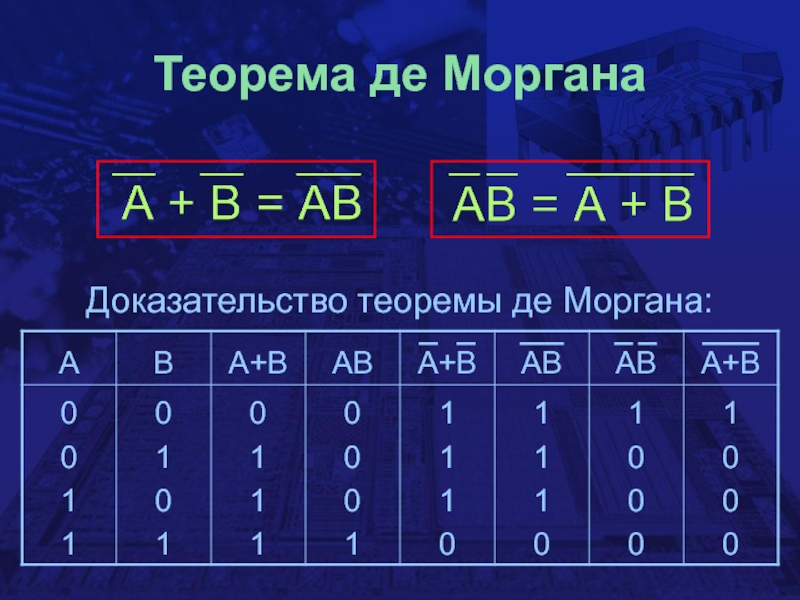
- 19. Теорема де МорганаДоказательство теоремы де Моргана:
- 20. Теорема де Моргана для 3-х и более переменных
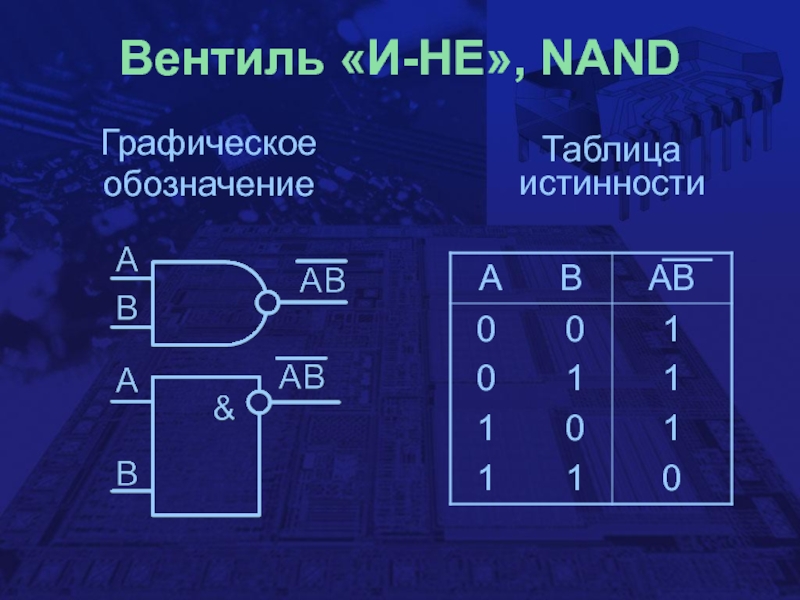
- 21. Вентиль «И-НЕ», NANDГрафическое обозначениеТаблица истинности
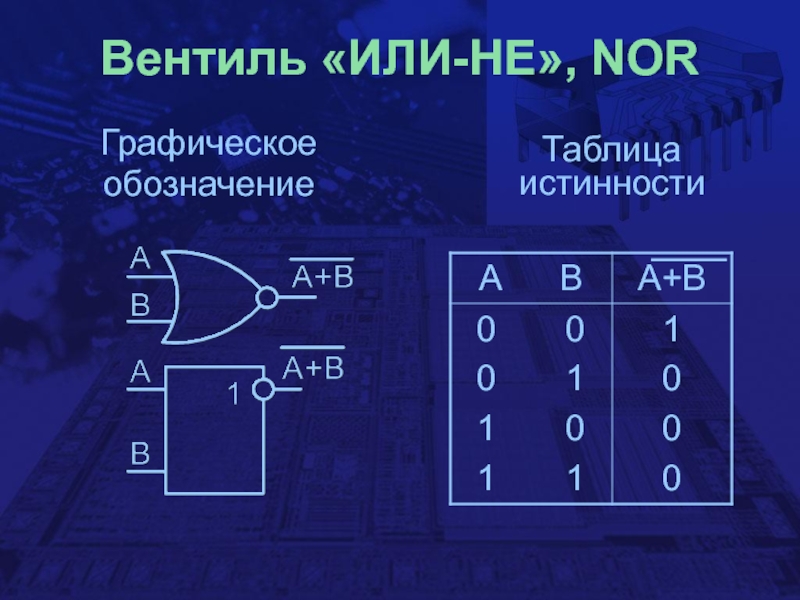
- 22. Вентиль «ИЛИ-НЕ», NOR Графическое обозначениеТаблица истинности
- 23. Универсальные вентили «И-НЕ», «ИЛИ-НЕ»
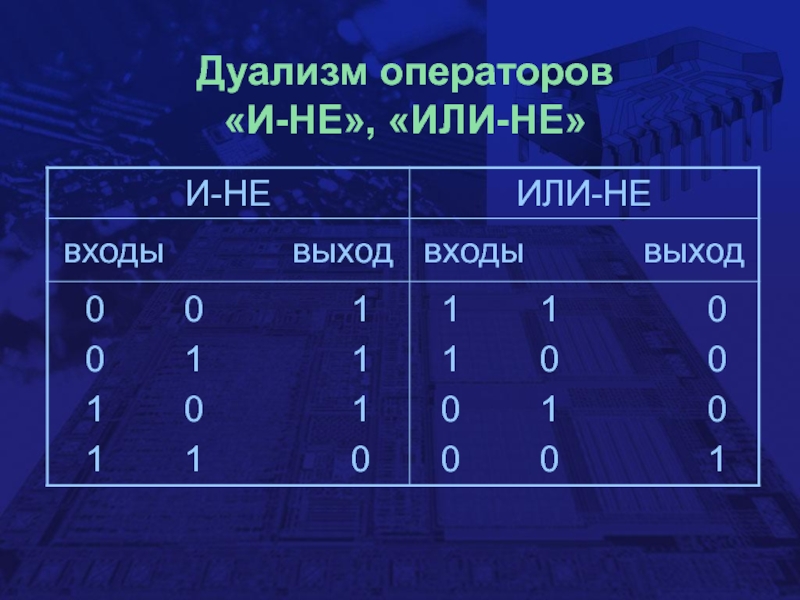
- 24. Дуализм операторов «И-НЕ», «ИЛИ-НЕ»
- 25. Вентиль «Исключающее ИЛИ»Определение: результат операции исключающее ИЛИ
- 26. Вентиль «Исключающее ИЛИ-НЕ»Определение: результат операции исключающее ИЛИ-НЕ
- 27. Коммутативные функцииF1 – операция ИF6 – операция
- 28. Итоги:В ходе лекции изучены:Базовые логические функции и
- 29. Скачать презентанцию
Цели и задачиЗнакомство с основными элементами цифровых схем – логическими вентилями.Рассмотрим различные типы логических вентилей.Знакомство с базовыми функциями булевой алгебры
Слайды и текст этой презентации
Слайд 4Вентиль «НЕ»
Определение: операция НЕ выполняется над одной переменной, и ее
результатом является логическое значение, противоположное исходному. Если А = 1,
то НЕ А = 0, а если А = 0, то НЕ А = 1.Графическое
обозначение
Таблица истинности
Слайд 5Вентиль «И»
Определение: результат операции И, выполняемой над переменными А и
В, равен 1, если А=1 «и» В=1; иначе результат равен
0.Графическое
обозначение
Таблица истинности
Слайд 7Вентиль «ИЛИ»
Определение: результат операции ИЛИ, выполняемой над переменными А и
В, равен 1, если А=1 «или» В=1, либо они обе
равны 1; иначе результат равен 0.Графическое
обозначение
Таблица истинности
Слайд 9Упрощенные определения
Если хотя бы один из входов вентиля «И» равен
0, то выход этого вентиля будет также равен 0, иначе
1.Если хотя бы один из входов вентиля «ИЛИ» равен 1, то выход этого вентиля будет также равен 1, иначе 0.
Слайд 10Булева алгебра
Разработана математиком Булем в ХIХ веке.
Использовалась для определения истинности
или ложности утверждений.
В цифровых схемах используется также, т.к. оперирует с
двузначными сигналами.
Слайд 11Основные булевы тождества
A·1 = A
A·0 = 0
A·A = A
A +
1 = 1
A + 0 = A
A + A =
AA·A = 0
A+A = 1
A = A
Доказательство:
Слайд 12Основные булевы тождества для нескольких переменных
A·B·1 = A·B
A·B·0 = 0
A·B·A
= A·B
A·B·A = 0
A+B+1 = 1
A+B+0 = A+B
A+B+A = A+B
A+B+A
= 1
Слайд 13Основные правила булевой алгебры
Закон коммутативности:
A · B = B ·
A
A + B = B + A
Закон ассоциативности:
ABС = A(BС)
= (AB)СA+B+С = A+(B+С) = (A+B)+С
Слайд 14Основные правила булевой алгебры
Закон дистрибутивности:
A (B + С) = AB
+ АС
A+(BС) = (A+B)(А+С)
!!! К арифметическому сложению Закон дистрибутивности
неприменим:A+(BС) ≠ (A+B)(А+С)
Слайд 15Положительная и отрицательная логика
Как изменятся таблицы истинности операций «И», «ИЛИ»,
«НЕ» для положительной и отрицательной логик?
Слайд 16Дуальные функции
В положительной логике:
f = A + BC
В отрицательной
логике:
f = A(B + C)
f = f (A, B,
C, …, ·, +, ,0, 1)fд = f (A, B, C, …, +, ·, ,1, 0)
Слайд 17Принцип дуализма
Если есть доказанное равенство:
f (A,B,C,…,·,+,0,1) = g (A,B,C,…,·,+,0,1)
Тогда справедливо
и дуальное ему равенство:
fд (A,B,C,…,·,+,0,1) = gд (A,B,C,…,·,+,0,1)
Чтобы получить дуальное
равенство необходимо заменить:«И» на «ИЛИ», «ИЛИ» на «И»
«0» на «1», «1» на «0»
Слайд 25Вентиль «Исключающее ИЛИ»
Определение: результат операции исключающее ИЛИ (Exclusive OR), выполняемой
над двумя переменными А и В, равен 0, если А=В,
иначе результат равен 1.Графическое обозначение
Таблица истинности
A⊕В = AB + AB
Слайд 26Вентиль «Исключающее ИЛИ-НЕ»
Определение: результат операции исключающее ИЛИ-НЕ (Exclusive NOR), выполняемой
над двумя переменными А и В, равен 1, если А=В,
иначе результат равен 0.Графическое обозначение
Таблица истинности
(A⊕В) = AB + AB
Слайд 27Коммутативные функции
F1 – операция И
F6 – операция исключающее ИЛИ
F7 –
операция ИЛИ
F8 – операция ИЛИ-НЕ
F9 – операция исключающее ИЛИ-НЕ
F14 –
операция И-НЕ
Слайд 28Итоги:
В ходе лекции изучены:
Базовые логические функции и вентили: И, ИЛИ,
НЕ
Основные тождества и правила булевой алгебры.
Положительная и отрицательная логика.
Принцип дуализма
логических функций и правило де Моргана.Универсальные вентили: И-НЕ, ИЛИ-НЕ
Функции «Исключающего ИЛИ» и «Исключающего ИЛИ-НЕ»
Полный набор логических функция для двух переменных.
