Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Структура и программная реализация цифровых фильтров и регуляторов
Содержание
- 1. Структура и программная реализация цифровых фильтров и регуляторов
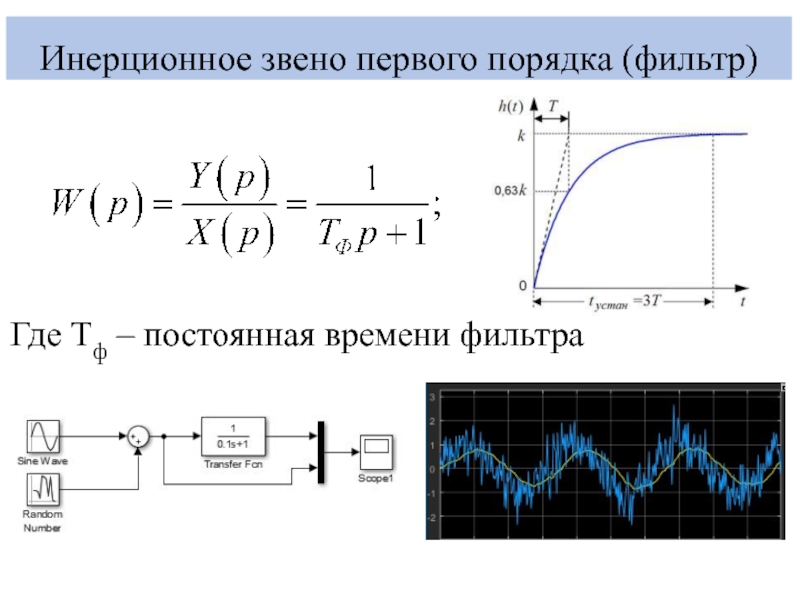
- 2. Инерционное звено первого порядка (фильтр)Где Тф – постоянная времени фильтра
- 3. Пример разработки и отладки программы инерционного звена
- 4. Пример разработки и отладки программы инерционного звена первого порядка (фильтра)
- 5. Пример разработки и отладки программы инерционного звена первого порядка (фильтра) void Filter_Init(){ ky1=_IQdiv(Th,Th+_IQ(1)); kx0=_IQdiv(_IQ(1),Th+_IQ(1));} void Filter_Execute(){ y=_IQmpy(kx0,x)+_IQmpy(ky1,y);}Пусть, тогда программный код:
- 6. Пример разработки и отладки программы инерционного звена
- 7. Пример разработки и отладки программы инерционного звена
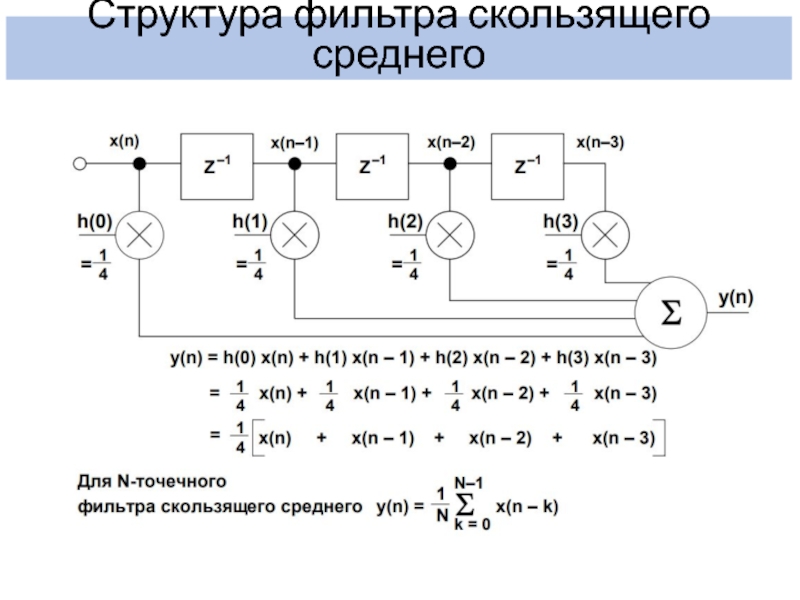
- 8. Структура фильтра скользящего среднего
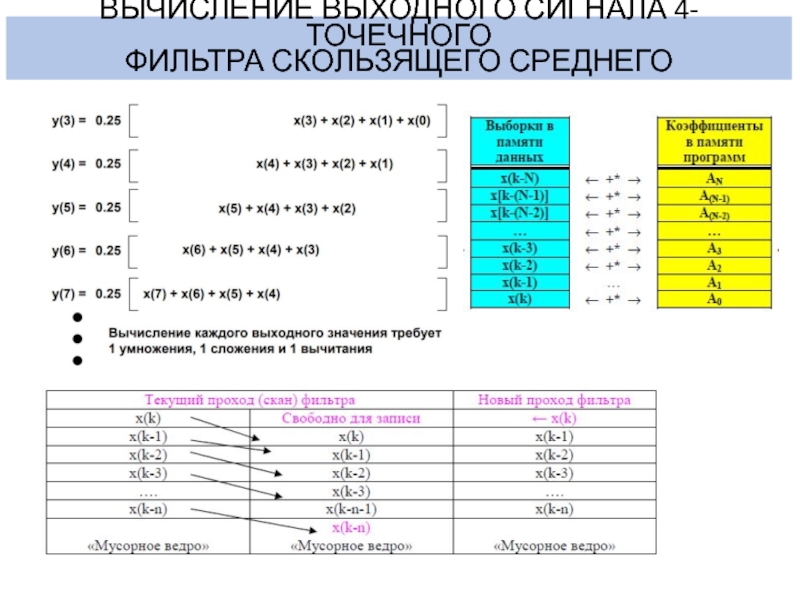
- 9. ВЫЧИСЛЕНИЕ ВЫХОДНОГО СИГНАЛА 4-ТОЧЕЧНОГОФИЛЬТРА СКОЛЬЗЯЩЕГО СРЕДНЕГО
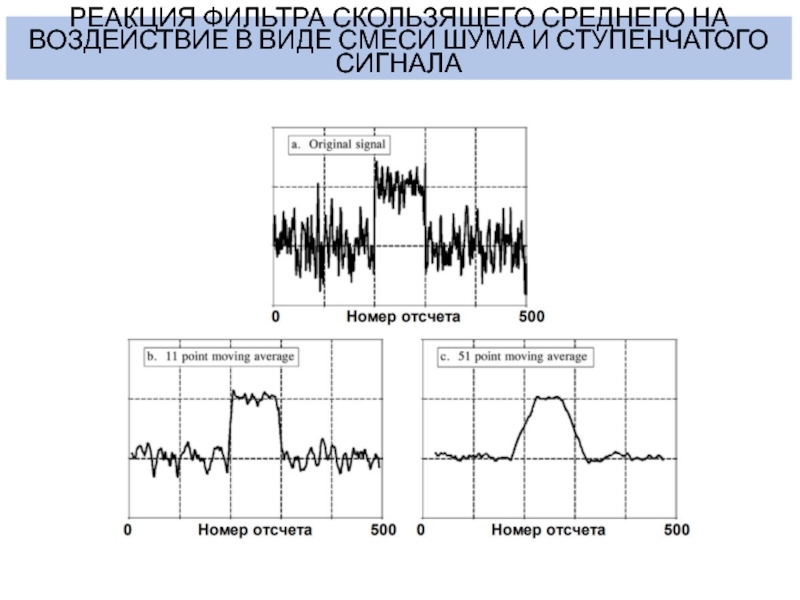
- 10. РЕАКЦИЯ ФИЛЬТРА СКОЛЬЗЯЩЕГО СРЕДНЕГО НА ВОЗДЕЙСТВИЕ В ВИДЕ СМЕСИ ШУМА И СТУПЕНЧАТОГО СИГНАЛА
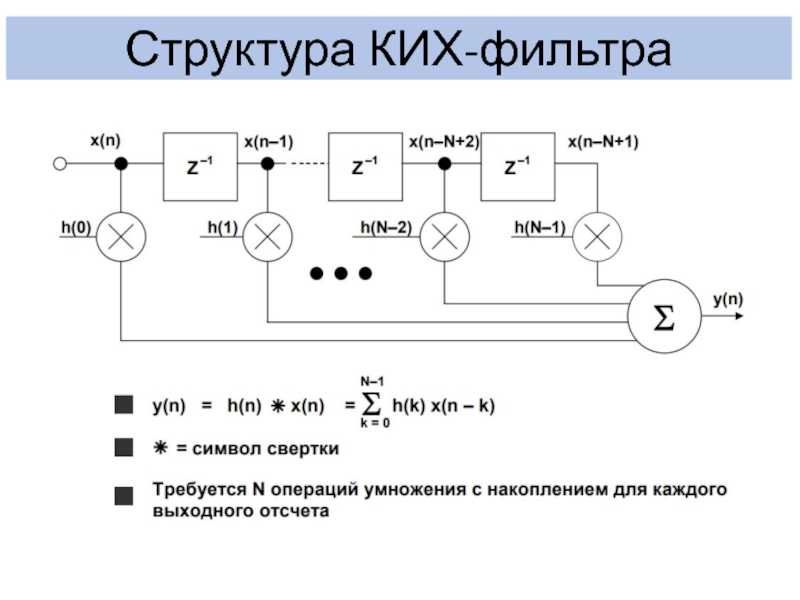
- 11. Структура КИХ-фильтра
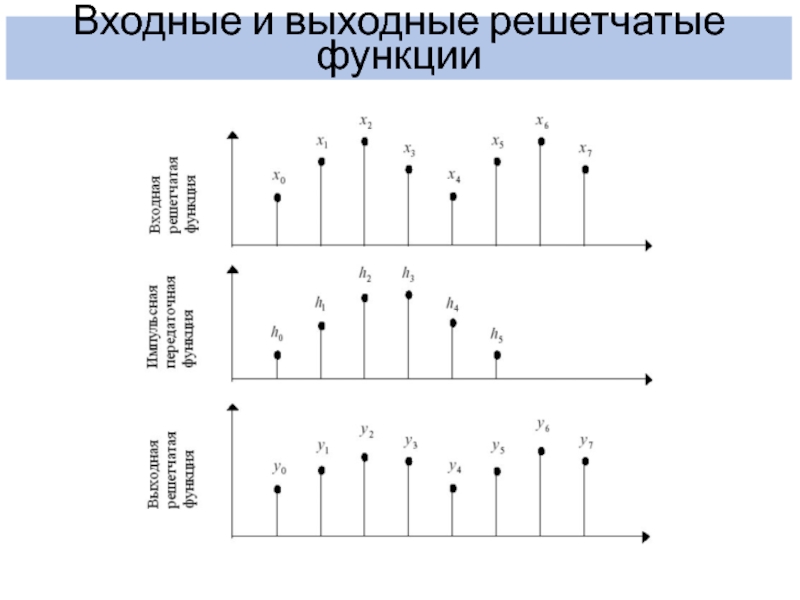
- 12. Входные и выходные решетчатые функции
- 13. ХАРАКТЕРИСТИКИ КИХ-ФИЛЬТРОВВыходное управляющее воздействие (результат работы фильтра)
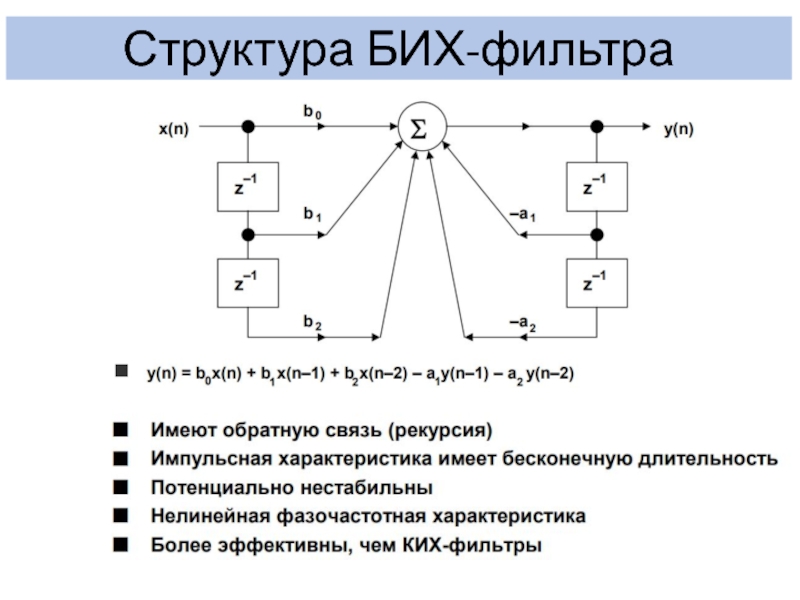
- 14. Структура БИХ-фильтра
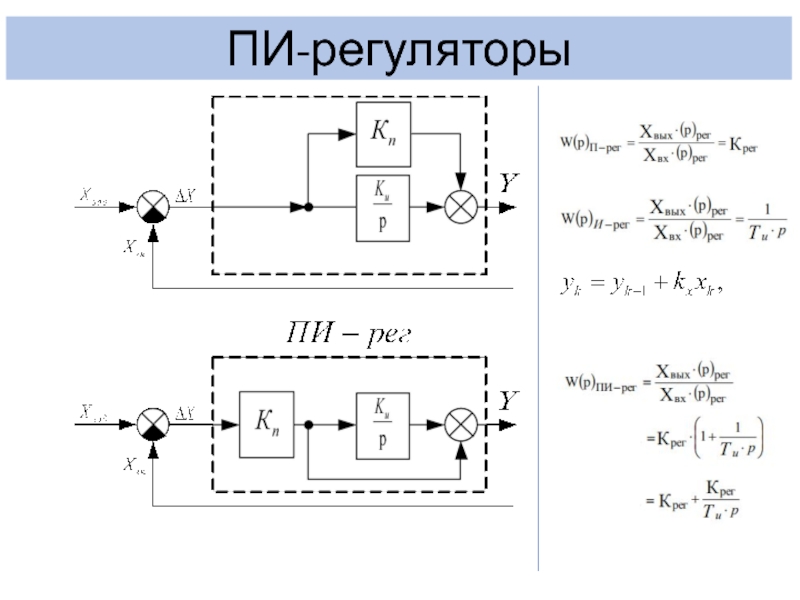
- 15. ПИ-регуляторы
- 16. Программная реализация ПИ-регулятора
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 5Пример разработки и отладки программы инерционного звена первого порядка (фильтра)
void
Filter_Init()
{
ky1=_IQdiv(Th,Th+_IQ(1));
kx0=_IQdiv(_IQ(1),Th+_IQ(1));
}
void Filter_Execute()
{
y=_IQmpy(kx0,x)+_IQmpy(ky1,y);
}
Пусть
, тогда программный код:
Слайд 6Пример разработки и отладки программы инерционного звена первого порядка (фильтра)
Можно
принять допущение и упростить формулы:
Приблизительно равен yk-1
Слайд 7Пример разработки и отладки программы инерционного звена первого порядка (фильтра)
Упрощенное
выражение фильтра
Это выражение имеет интуитивно-понятный смысл:
На данном шаге расчета отфильтрованное
значение (yk) равно тому же самому, чему было равно в прошлый раз (yk-1) плюс коррекция, которая пропорциональна разнице между входом фильтра и его выходным значением. Чем отношение h/Tф больше, тем коррекция сильнее, соответственно фильтр работает «быстрее» и фильтрует слабее.Программная реализация также проста и делается одной строкой:
output = output + _IQmpy(kf,(input-output));
Где kf – коэффициент фильтра, равный h/Tф : отношению частоты вызова функции фильтра h к желаемой постоянной времени Tф.
Слайд 10РЕАКЦИЯ ФИЛЬТРА СКОЛЬЗЯЩЕГО СРЕДНЕГО НА ВОЗДЕЙСТВИЕ В ВИДЕ СМЕСИ ШУМА
И СТУПЕНЧАТОГО СИГНАЛА
Слайд 13ХАРАКТЕРИСТИКИ КИХ-ФИЛЬТРОВ
Выходное управляющее воздействие (результат работы фильтра) представляет собой сумму
произведений величин, сохраненных в линии задержки, на соответствующие коэффициенты. Заметьте,
что число коэффициентов в фильтре всегда на единицу больше, чем порядок фильтра. Это связано с тем, что текущая выборка x(n), которая представляет собой входное воздействие, всегда участвует в процессе вычислений.Если предположить, что буфер выборок вначале пуст, то выходное значение y0 будет рассчитываться только на основе входной выборки x0, выходное значение y1 уже на основе двух выборок x0 и x1 и т.д. Начиная с шестой выборки x5, все предыдущие выборки будут участвовать в расчете выходной переменной фильтра, т.е. буфер выборок окажется полностью заполненным.