Слайд 2Магнитные явления были известны еще в древнем мире. Компас был
изобретен более 4500 лет тому назад.
Он появился в Европе приблизительно
в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле
.
Слайд 3Первыми экспериментами, показавшими, что между электрическими и магнитными явлениями имеется
глубокая связь, были опыты датского физика Х. Эрстеда (1820 г.). Эти
опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся повернуть стрелку
Слайд 4В 1820 году французский физик А. Ампер установил закон взаимодействия
токов.
Проводники с током оказывают силовое действие друг на друга
не непосредственно, а через окружающие их магнитные поля.
Все свойства магнитной силы можно описать, если ввести понятие магнитного поля.
Это поле характеризуется магнитной индукцией В.
Слайд 5Тогда полная электромагнитная сила, действующая на заряд q:
Эту силу называют
силой Лоренца. Она состоит из электрической и магнитной составляющих.
Магнитное
поле действует на движущейся электрический заряд с силой
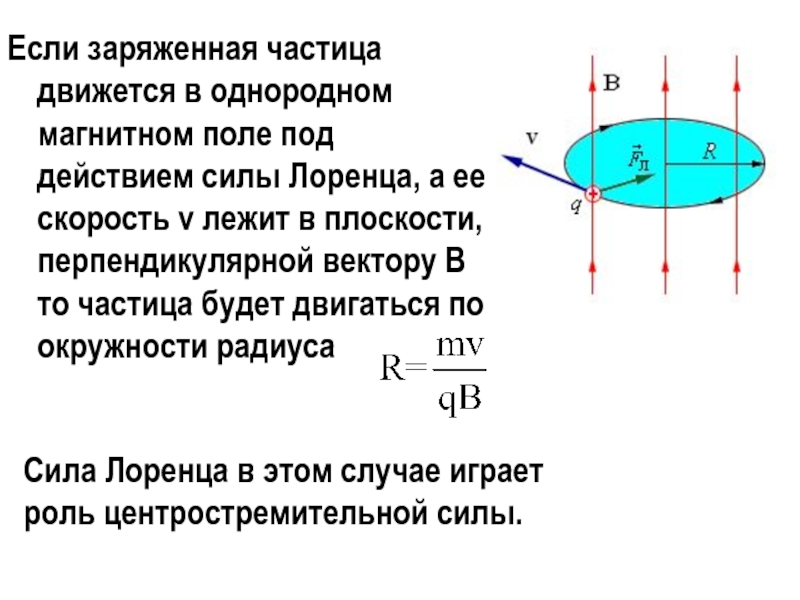
Слайд 6Если заряженная частица движется в однородном магнитном поле под действием
силы Лоренца, а ее скорость v лежит в плоскости, перпендикулярной
вектору B то частица будет двигаться по окружности радиуса
Сила Лоренца в этом случае играет роль центростремительной силы.
Слайд 7Период обращения частицы в однородном магнитном поле равен
Это выражение
показывает, что для заряженных частиц заданной массы m период обращения
не зависит от скорости v и радиуса траектории R. Угловая скорость движения заряженной частицы по круговой траектории:
Называется циклотронной частотой.
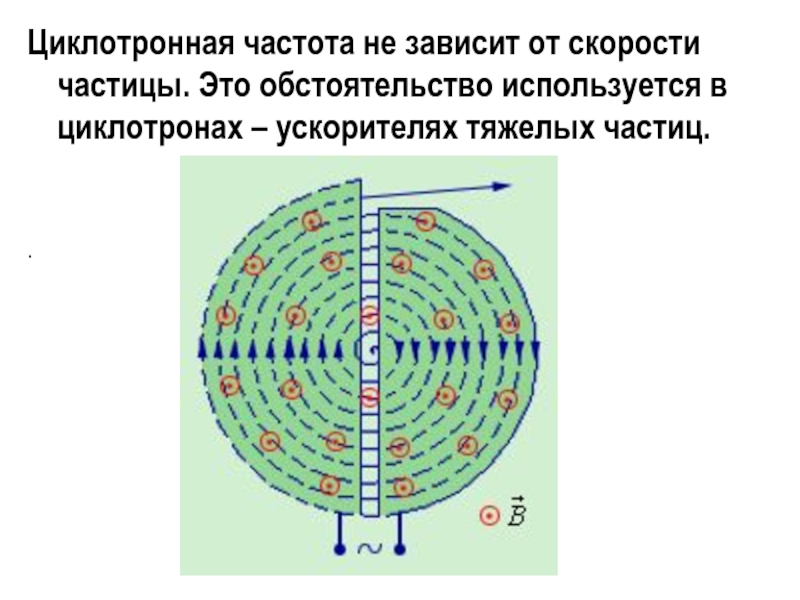
Слайд 8Циклотронная частота не зависит от скорости частицы. Это обстоятельство используется
в циклотронах – ускорителях тяжелых частиц.
.
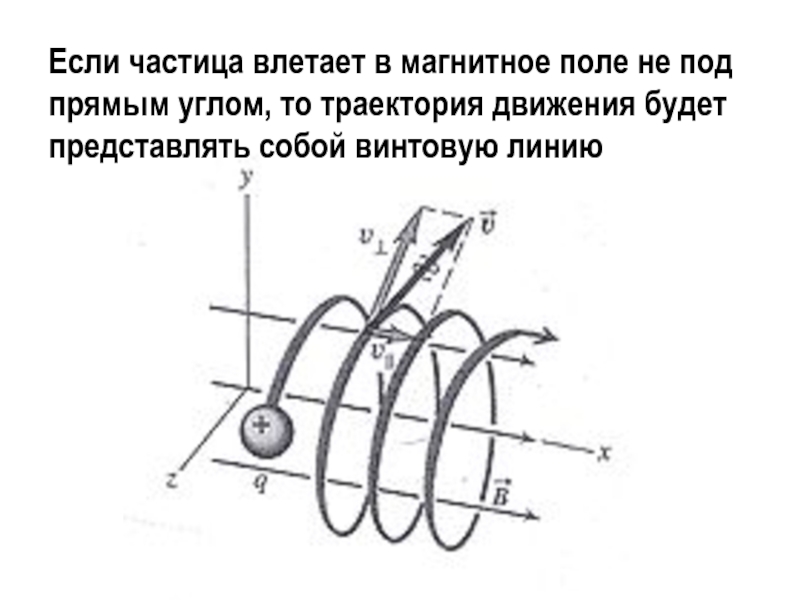
Слайд 9Если частица влетает в магнитное поле не под прямым углом,
то траектория движения будет представлять собой винтовую линию
Слайд 10 Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное
поле возникает в пространстве, окружающем проводники с током, подобно тому,
как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).
.
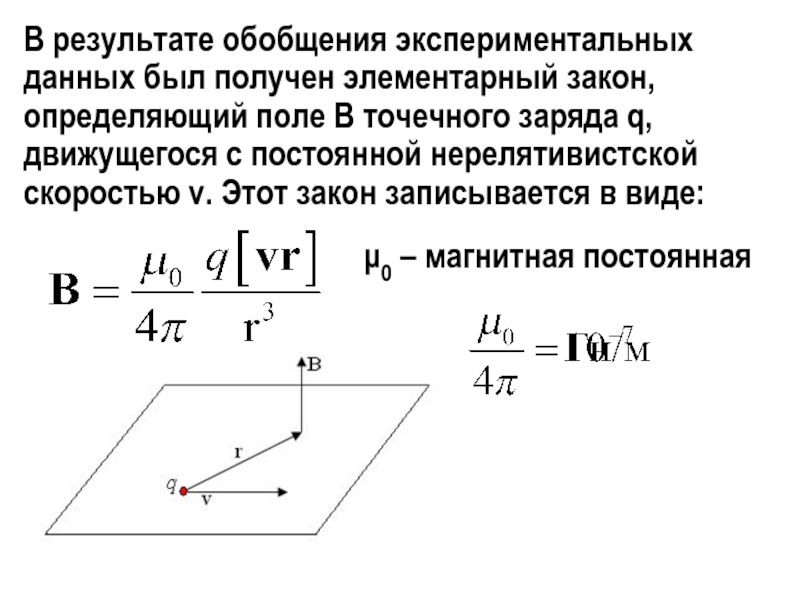
Слайд 11В результате обобщения экспериментальных данных был получен элементарный закон, определяющий
поле В точечного заряда q, движущегося с постоянной нерелятивистской скоростью
v. Этот закон записывается в виде:
μ0 – магнитная постоянная
Слайд 12 Магнитное поле постоянных токов различной конфигурации изучалось
экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они
пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции: магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом или током в отдельности.
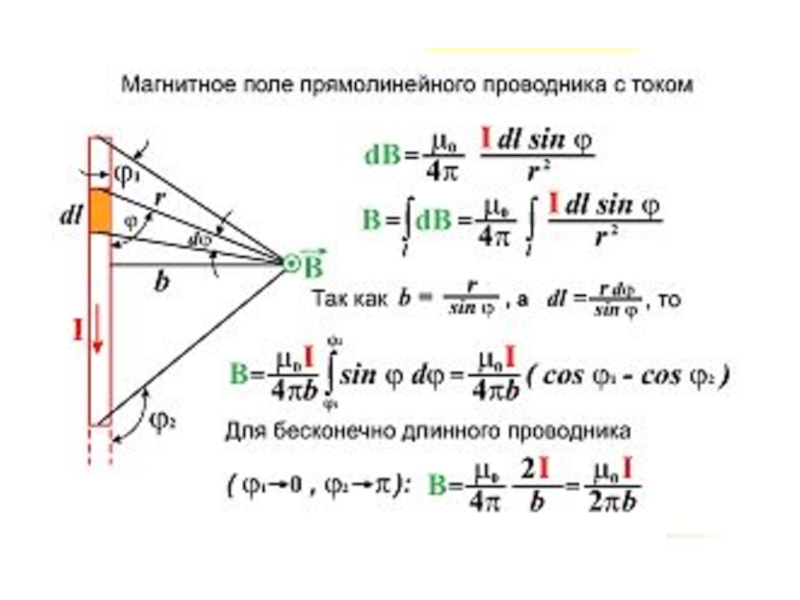
Слайд 13Закон Био-Савара-Лапласа
Элементарный заряд q равен ρdV, где dV
– элементарный объем, ρ – объемная плотность заряда, являющегося носителем
тока, учтем также, что ρv=j плотность тока. Тогда магнитное поле, создаваемое таким зарядом равно:
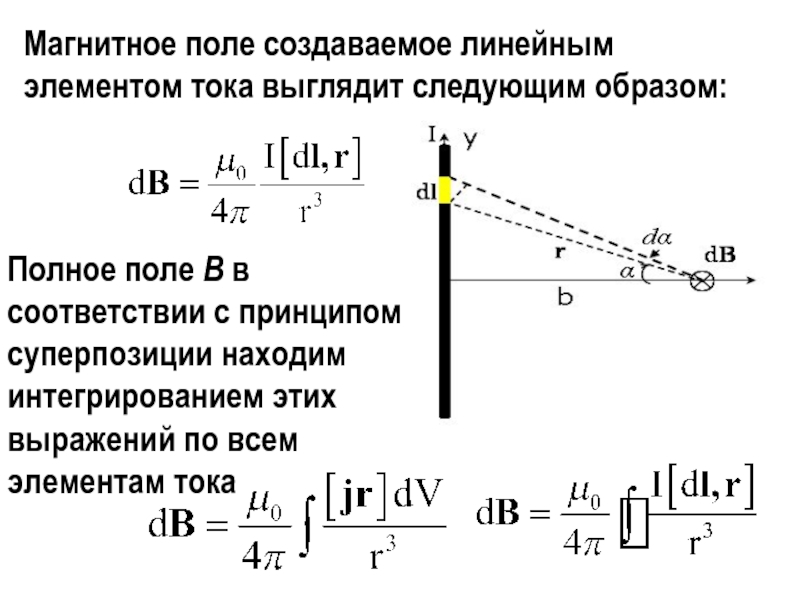
Слайд 14Магнитное поле создаваемое линейным элементом тока выглядит следующим образом:
Полное
поле В в соответствии с принципом суперпозиции находим интегрированием этих
выражений по всем элементам тока
Слайд 16 Как и любое другое векторное поле, поле В
может быть представлено наглядно с помощью силовых линий вектора В.
Их проводят так, чтобы касательная к этим линиям в каждой точке совпадала с направлением вектора В, а густота линий была бы пропорциональна модулю вектора В в данном месте.
Слайд 17Магнитное поле обладает, как и электрическое поле, двумя важнейшими свойствами
– поток и циркуляция вектора В. Поток вектора В сквозь
любую замкнутую поверхность равен нулю:
Равенство потока вектора В нулю также является следствием того, что в природе не существует магнитных зарядов на которых начинались бы или заканчивались линии магнитной индукции В.
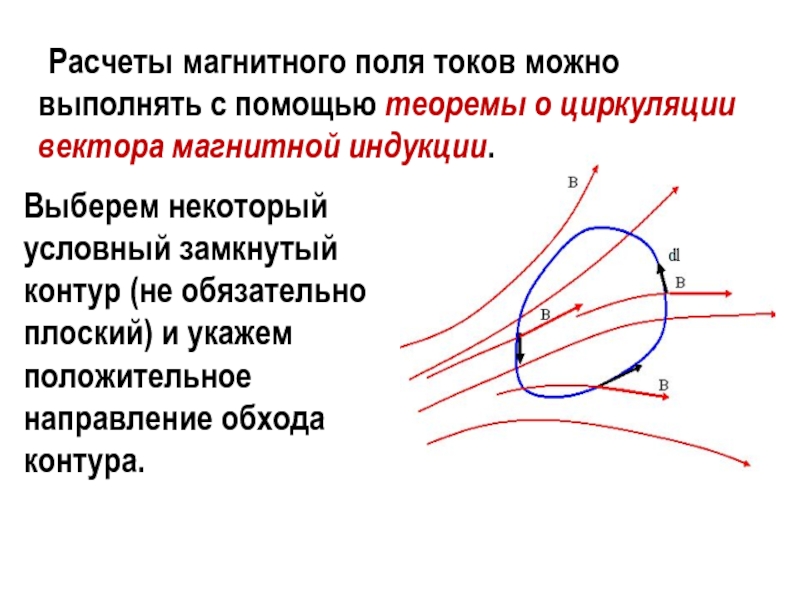
Слайд 18 Расчеты магнитного поля токов можно выполнять с
помощью теоремы о циркуляции вектора магнитной индукции.
Выберем некоторый условный замкнутый
контур (не обязательно плоский) и укажем положительное направление обхода контура.
Слайд 19 Теорема о циркуляция вектора В: циркуляция вектора
В по произвольному контуру равна произведению μ0 на алгебраическую сумму
токов, охватываемых контуром:
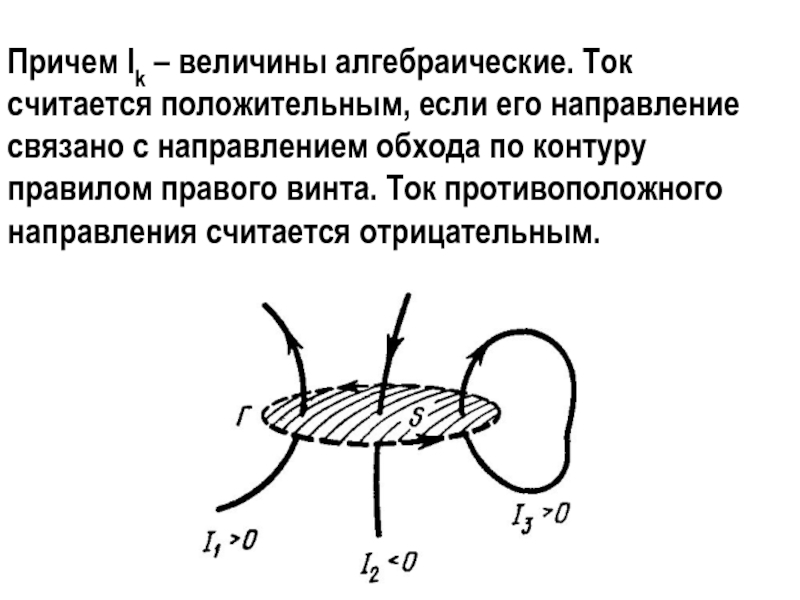
Слайд 20Причем Ik – величины алгебраические. Ток считается положительным, если его
направление связано с направлением обхода по контуру правилом правого винта.
Ток противоположного направления считается отрицательным.
Слайд 21 Каждый носитель тока испытывает действие магнитной силы.
Действие этой силы передается проводнику, по которому движутся заряды. В
результате магнитное поле действует с определенной силой на сам проводник с током.
Слайд 22Пусть объемная плотность заряда, являющегося носителем тока равна ρ. Выделим
мысленно элемент объема dV проводника. В нем находится заряд –
носитель тока, равный ρdV.
Тогда сила, действующая на элемент dV проводника, может быть записана в виде:
Слайд 23Закон Ампера
Если ток течет по тонкому проводнику, то так как
получим
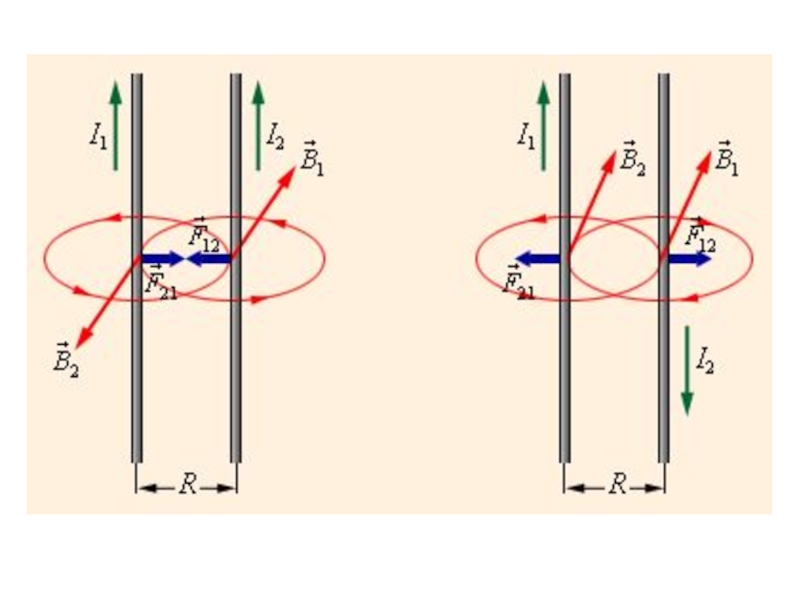
Слайд 25Между проводниками возникают силы притяжения или отталкивания, обусловленные магнитным взаимодействием
токов.
Токи, одинаково направленные, притягиваются, а противоположно направленные – отталкиваются.
Слайд 26Результирующая сила Ампера, которая действует на контур с током в
магнитном поле, определяется интегрированием по данному контуру с током:
В однородном
магнитном поле результирующая сила Ампера равна нулю.
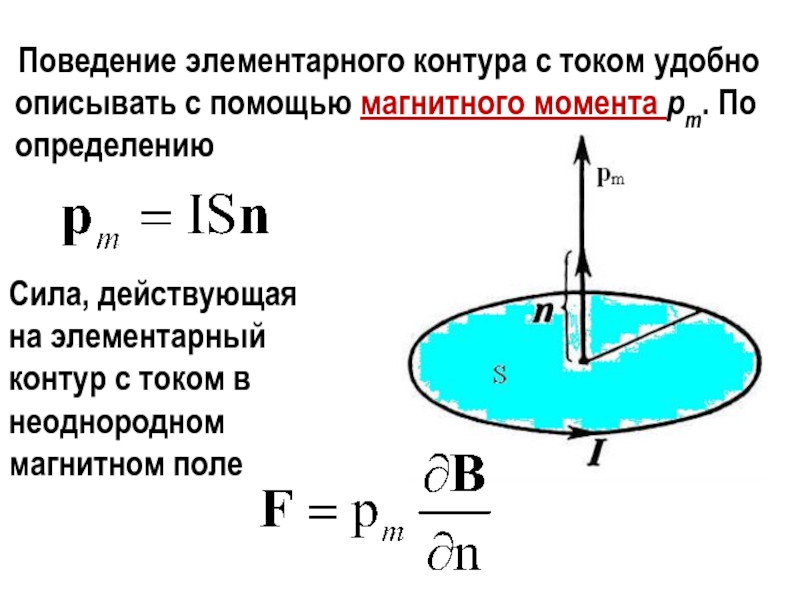
Слайд 27 Поведение элементарного контура с током удобно описывать с
помощью магнитного момента pm. По определению
Сила, действующая на элементарный
контур с током в неоднородном магнитном поле
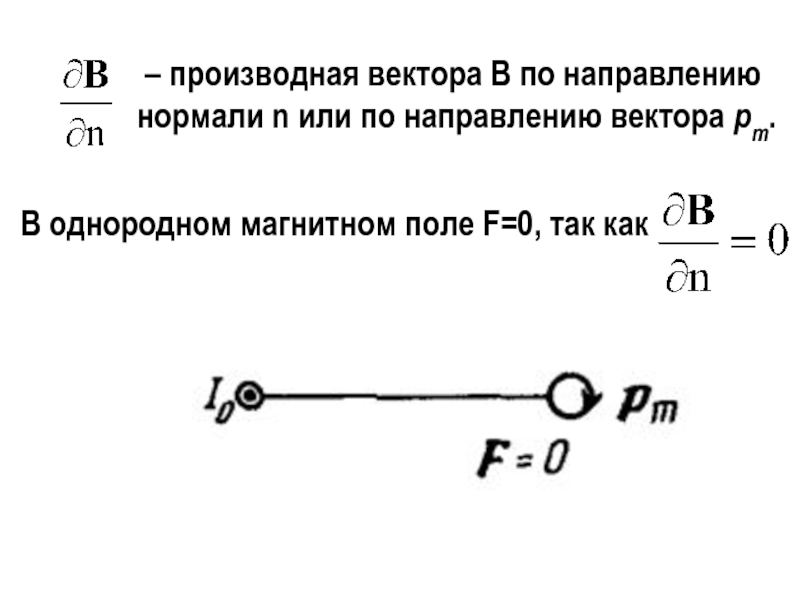
Слайд 28 – производная вектора В по направлению нормали n или
по направлению вектора pm.
В однородном магнитном поле F=0, так
как
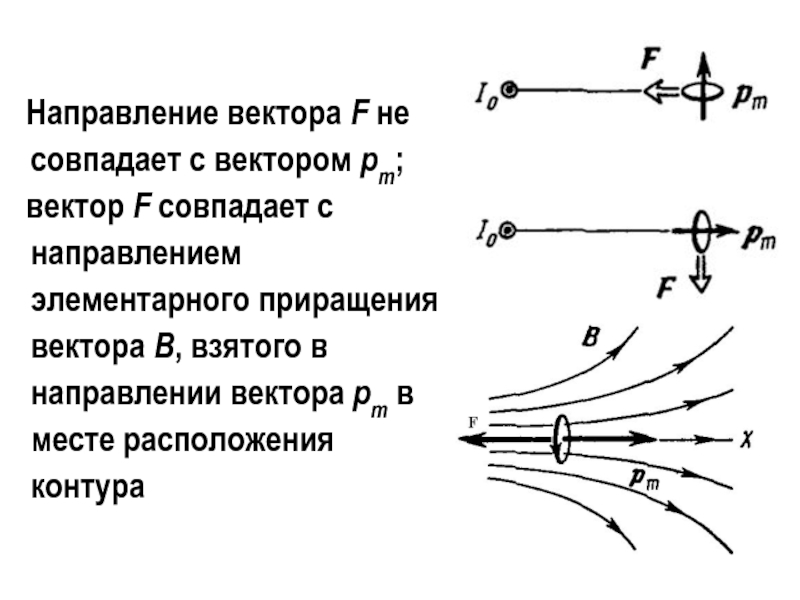
вектора F не совпадает с вектором pm;
вектор F совпадает с направлением элементарного приращения вектора B, взятого в направлении вектора pm в месте расположения контура
Слайд 30 Найдем момент сил (вращательный момент), действующий на
контур с током в однородном магнитном поле.
Учтем, что если результирующая сил равна нулю, то момент сил не зависит от выбора точки, относительно которой он вычисляется.
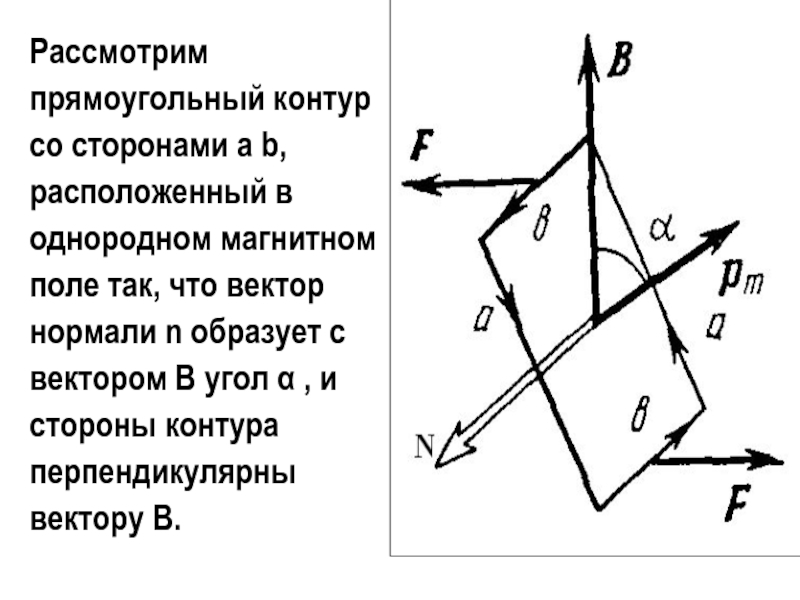
Слайд 31Рассмотрим прямоугольный контур со сторонами a b, расположенный в однородном
магнитном поле так, что вектор нормали n образует с вектором
В угол , и стороны контура перпендикулярны вектору В.
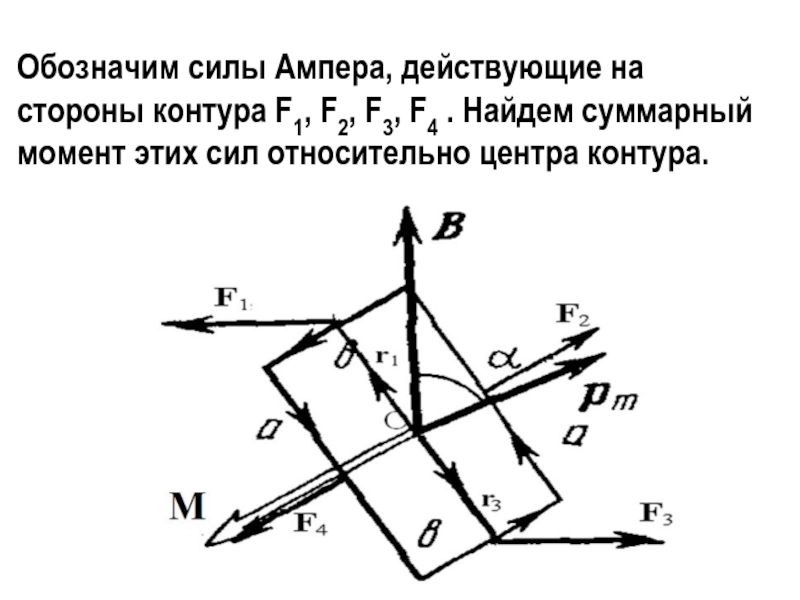
Слайд 32Обозначим силы Ампера, действующие на стороны контура F1, F2, F3,
F4 . Найдем суммарный момент этих сил относительно центра контура.
Слайд 33Линии действия сил F2,F4 проходят через точку О, следовательно, моменты
этих сил равны нулю.
Две другие силы: F1 и F3
и радиус-векторы точек их приложения r1 и r3 лежат в плоскости, образованной векторами B и n . Каждая из сил F1, F3 перпендикулярна вектору В, а радиус-векторы r1, r3 перпендикулярны вектору n. Поэтому силы F1, F3 образуют с радиус-векторами r1, r3 тот же угол , что и вектор B с нормалью n. Момент этих сил M равен
M=[r1,F1]+[r2,F2]
Слайд 34Слагаемые в этой сумме направлены в одну сторону. По формуле
(для силы Ампера) обе силы равны F1=F2=IaB, кроме того, r1=r2=a/2.
Поэтому слагаемые одинаковы по величине и равны
M=IBabsinα=IBSsinα
Слайд 35Можно записать величину момента сил Ампера, действующих на этот контур
Векторы
pm, B, M составляют правую тройку векторов, поэтому в общем
виде получаем:
Слайд 36Момент сил Ампера обращается в нуль при = 0
и = .
В остальных случаях вращающий момент, действующий
на контур с током, стремится развернуть контур так, чтобы направление магнитного момента контура совпало с направлением магнитной индукции внешнего поля, т.е. к состоянию = 0.
Поэтому при = 0 контур оказывается в устойчивом равновесии, а при = – в неустойчивом.
Слайд 37Контрольные вопросы
Закон Био-Савара-Лапласа
Поток вектора магнитной индукции. Следствие из определения потока.
Теорема
о циркуляции вектора магнитной индукции
Сила Ампера
Магнитный момент. Момент силы Ампера.