Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Магнитное поле в вакууме Основные уравнения магнитного поля Уравнения
Содержание
- 1. Магнитное поле в вакууме Основные уравнения магнитного поля Уравнения
- 2. Магнитное поле в вакуумеОсновные уравнения магнитного поляТеорема
- 3. Магнитное поле в вакуумеПрименение теоремы о циркуляции
- 4. Магнитное поле в вакуумеПрименение теоремы о циркуляции
- 5. Магнитное поле в вакуумеВектор-потенциалПо закону Био-Савара….ОтсюдаПо аналогии суравнение для вектор-потенциалаA – вектор-потенциал магнитного поляO
- 6. Магнитное поле в вакуумеМагнитный дипольМагнитный диполь –
- 7. Магнитное поле в вакуумеМагнитный дипольВзаимодействие диполя с
- 8. Магнитное поле в вакуумеПрецессия магнитного диполя. Магнитный
- 9. Магнитное поле в вакуумеПрецессия магнитного диполя. Магнитный
- 10. Магнитное поле в вакуумеПрецессия магнитного диполя. Магнитный
- 11. Магнитное поле в вакуумеРабота по перемещению контура
- 12. Магнитное поле в вакуумеДавление магнитного поля“прямоугольный” соленоидобъемная
- 13. Электромагнитная индукцияЗакон электромагнитной индукции. Правило Ленца– магнитный
- 14. Электромагнитная индукцияЗакон электромагнитной индукции. Правило ЛенцаСпособы возбуждения
- 15. Электромагнитная индукцияПрирода электромагнитной индукцииВозбуждение ЭДС в контуре
- 16. Электромагнитная индукцияПрирода электромагнитной индукцииВозбуждение ЭДС в контуре
- 17. Электромагнитная индукцияПрирода электромагнитной индукцииО единой природе ЭДС
- 18. Электромагнитная индукцияЯвление самоиндукцииЯвление самоиндукции – при изменении
- 19. Электромагнитная индукцияЯвление самоиндукцииИндуктивность соленоида– плотность намотки– поток через один виток– полный поток
- 20. Электромагнитная индукцияВзаимная индукцияikТак как– взаимная индуктивность контуров
- 21. Электромагнитная индукцияМагнитная энергия токовikКонтуры неподвижны. A –
- 22. Электромагнитная индукцияМагнитная энергия токовТаким образом. . .
- 23. Электромагнитная индукцияЭнергетический метод определения силСистема токов в
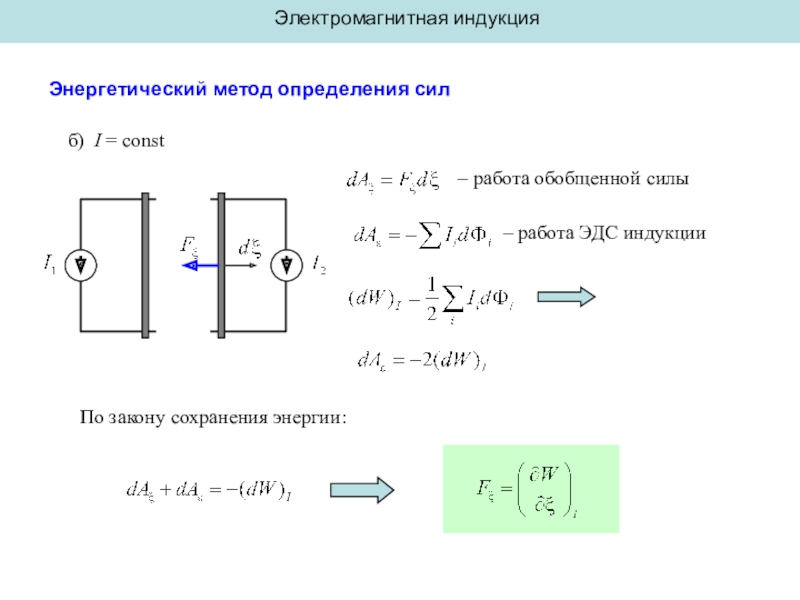
- 24. Электромагнитная индукцияЭнергетический метод определения силб) I =
- 25. Электромагнитная индукцияЭнергетический метод определения силПример: давление магнитного поля на стенку соленоида
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Магнитное поле в вакууме
Основные уравнения магнитного поля
Уравнения магнитостатики:
Теорема Гаусса для
вектора B
теорема Гаусса для B (интегральная форма)Слайд 2Магнитное поле в вакууме
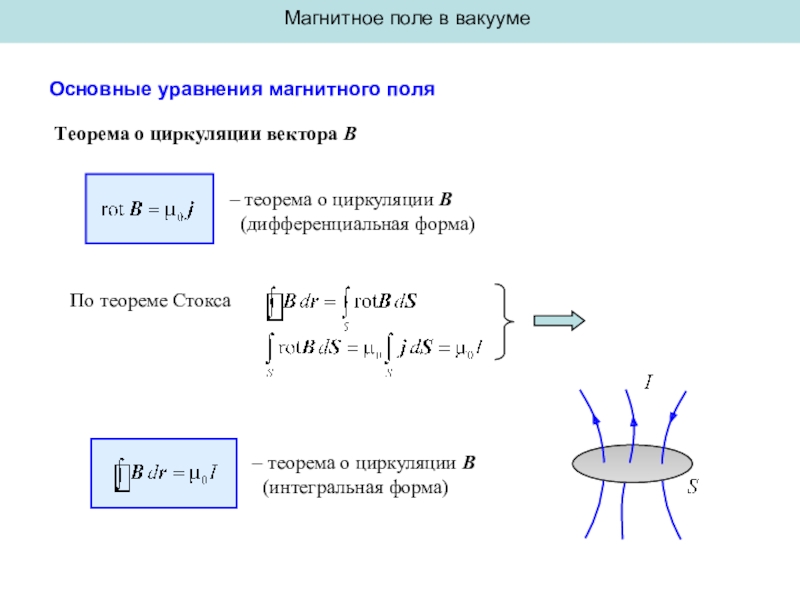
Основные уравнения магнитного поля
Теорема о циркуляции вектора
B
– теорема о циркуляции B
(дифференциальная форма)
По теореме Стокса
– теорема
о циркуляции B
(интегральная форма)Слайд 3Магнитное поле в вакууме
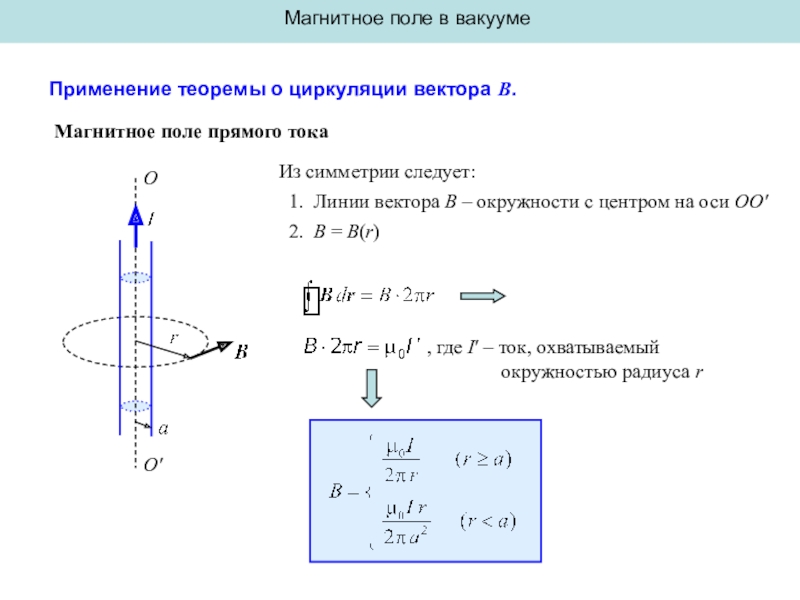
Применение теоремы о циркуляции вектора B.
Магнитное поле
прямого тока
O'
O
Из симметрии следует:
1. Линии вектора B – окружности
с центром на оси OO'
2. B = B(r), где I – ток, охватываемый
окружностью радиуса r
Слайд 4Магнитное поле в вакууме
Применение теоремы о циркуляции вектора B
Магнитное поле
соленоида
z
Из симметрии следует:
1. B z
2. B
= B(r), вне соленоида B = 0, где n – плотность намотки (N/L),
I – ток в проводе
nI – число ампервитков
Слайд 5Магнитное поле в вакууме
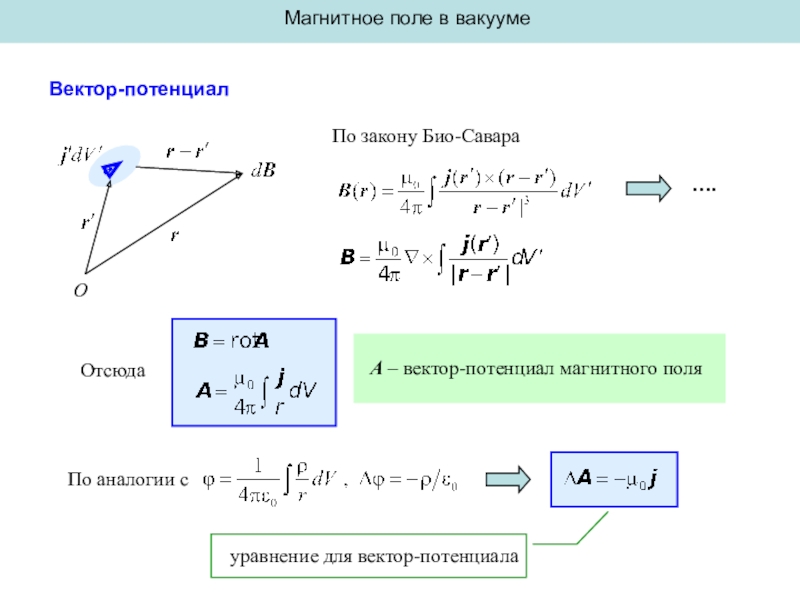
Вектор-потенциал
По закону Био-Савара
….
Отсюда
По аналогии с
уравнение для вектор-потенциала
A
– вектор-потенциал магнитного поля
O
Слайд 6Магнитное поле в вакууме
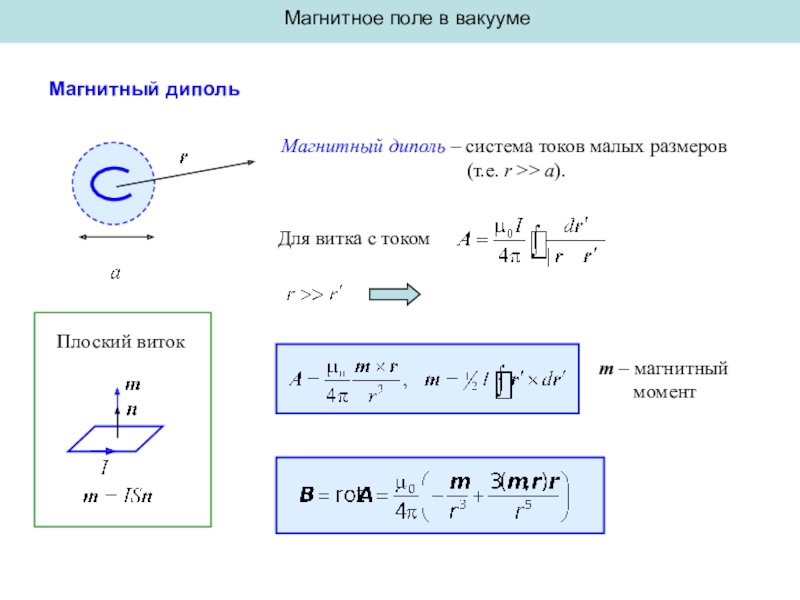
Магнитный диполь
Магнитный диполь – система токов малых
размеров
(т.е. r >> a).Для витка с током
m – магнитный
момент
Плоский виток
Слайд 7Магнитное поле в вакууме
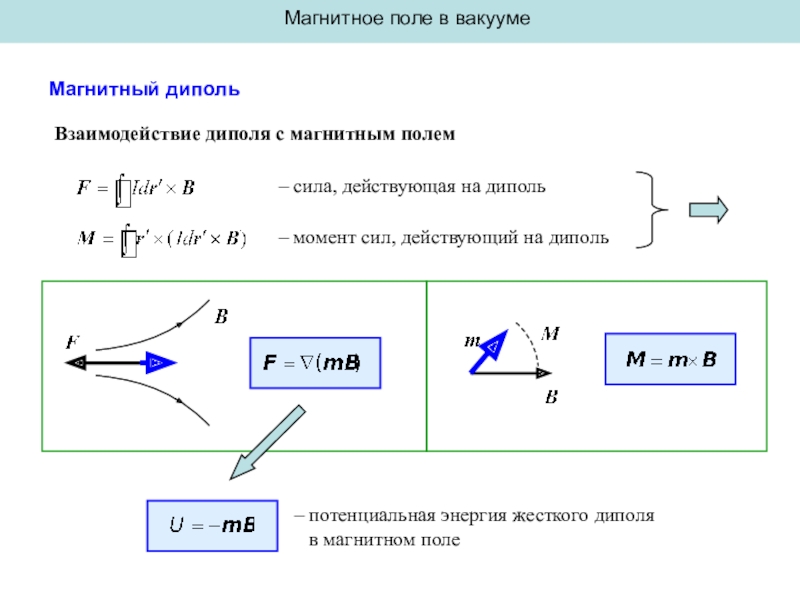
Магнитный диполь
Взаимодействие диполя с магнитным полем
–
сила, действующая на диполь
– момент сил, действующий на диполь
– потенциальная
энергия жесткого диполя
в магнитном поле Слайд 8Магнитное поле в вакууме
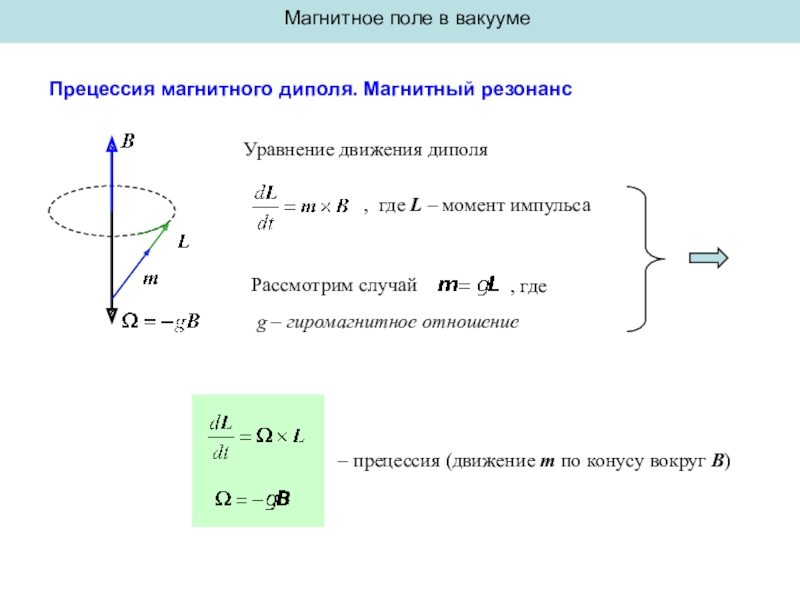
Прецессия магнитного диполя. Магнитный резонанс
Уравнение движения диполя
Рассмотрим
случай
, где L – момент импульса
, где
– прецессия (движение m
по конусу вокруг B)g – гиромагнитное отношение
Слайд 9Магнитное поле в вакууме
Прецессия магнитного диполя. Магнитный резонанс
Составные системы (атомы,
молекулы)
, m прецессирует вокруг L
В среднем
– прецессия , L
вокруг B(в слабых полях)
Гиромагнитное отношение g сложной системы позволяет судить об ее “устройстве”.
Слайд 10Магнитное поле в вакууме
Прецессия магнитного диполя. Магнитный резонанс
Магнитный резонанс
B0 –
постоянное магнитное поле
B – слабое вращающееся поперечное
магнитное полеПри = возникает резонанс –
происходит переворачивание m и поглощение энергии генератора B
Из измеренных и B0 находится g
Применение магнитного резонанса
ЭПР (электронный парамагнитный резонанс) – резонанс магнитных моментов атомов и молекул:
анализ химического состава вещества
ЯМР (ядерный магнитный резонанс) – резонанс магнитных моментов ядер:
прецизионное измерение B,
анализ строения молекул
Слайд 11Магнитное поле в вакууме
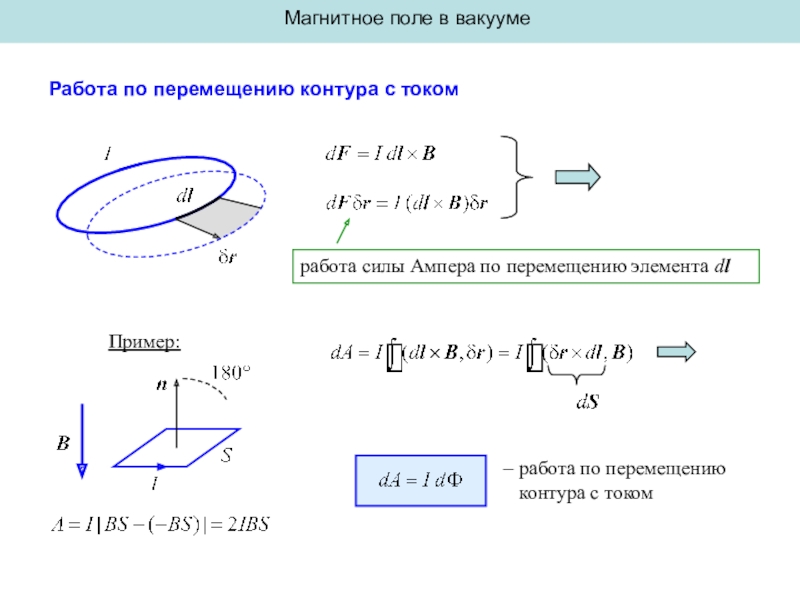
Работа по перемещению контура с током
работа силы
Ампера по перемещению элемента dl
– работа по перемещению
контура
с токомПример:
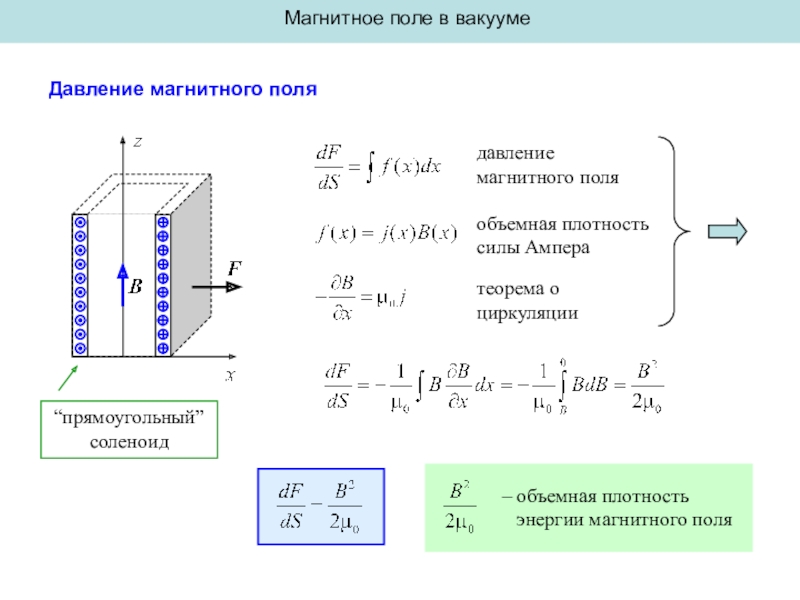
Слайд 12Магнитное поле в вакууме
Давление магнитного поля
“прямоугольный” соленоид
объемная плотность силы Ампера
теорема
о циркуляции
давление магнитного поля
– объемная плотность
энергии магнитного поля
Слайд 13Электромагнитная индукция
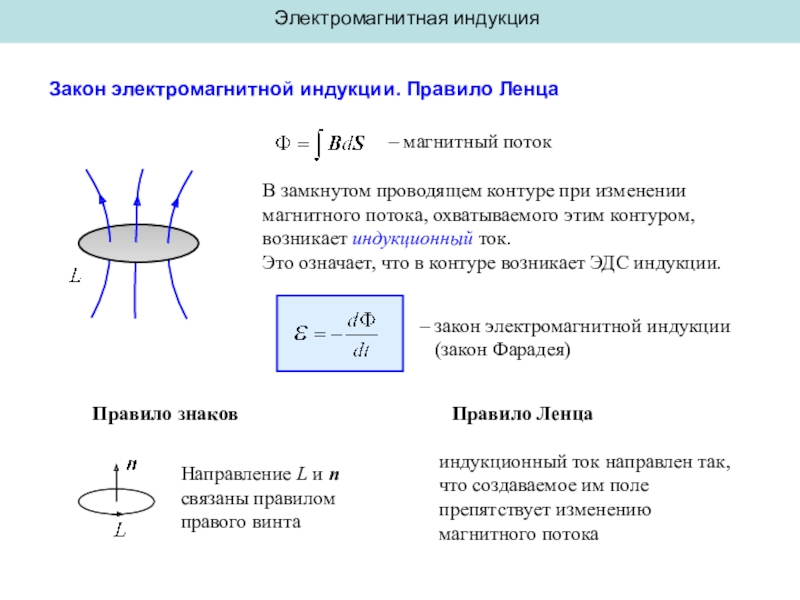
Закон электромагнитной индукции. Правило Ленца
– магнитный поток
В замкнутом проводящем
контуре при изменении магнитного потока, охватываемого этим контуром, возникает индукционный
ток. Это означает, что в контуре возникает ЭДС индукции.– закон электромагнитной индукции
(закон Фарадея)
Правило знаков
Направление L и n
связаны правилом
правого винта
Правило Ленца
индукционный ток направлен так, что создаваемое им поле препятствует изменению
магнитного потока
Слайд 14Электромагнитная индукция
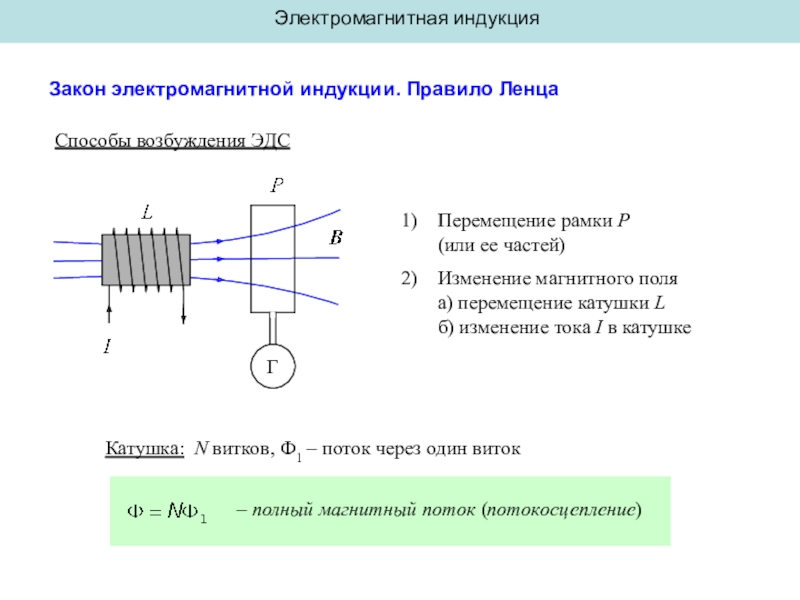
Закон электромагнитной индукции. Правило Ленца
Способы возбуждения ЭДС
Г
Перемещение рамки Р
(или
ее частей)
Изменение магнитного поля
а) перемещение катушки L
б) изменение тока I
в катушкеКатушка: N витков, Ф1 – поток через один виток
– полный магнитный поток (потокосцепление)
Слайд 15Электромагнитная индукция
Природа электромагнитной индукции
Возбуждение ЭДС в контуре при его движении
в постоянном магнитном поле
v – скорость элемента контура dl и
электронов
проводимостиСторонняя сила – магнитная составляющая силы Лоренца
Слайд 16Электромагнитная индукция
Природа электромагнитной индукции
Возбуждение ЭДС в контуре в переменном магнитном
поле
Сторонняя сила – электрическое (вихревое) поле, поскольку магнитная составляющая силы
Лоренца отсутствует (контур покоится).– потенциальное электрическое поле
– вихревое электрическое поле
В общем случае
Слайд 17Электромагнитная индукция
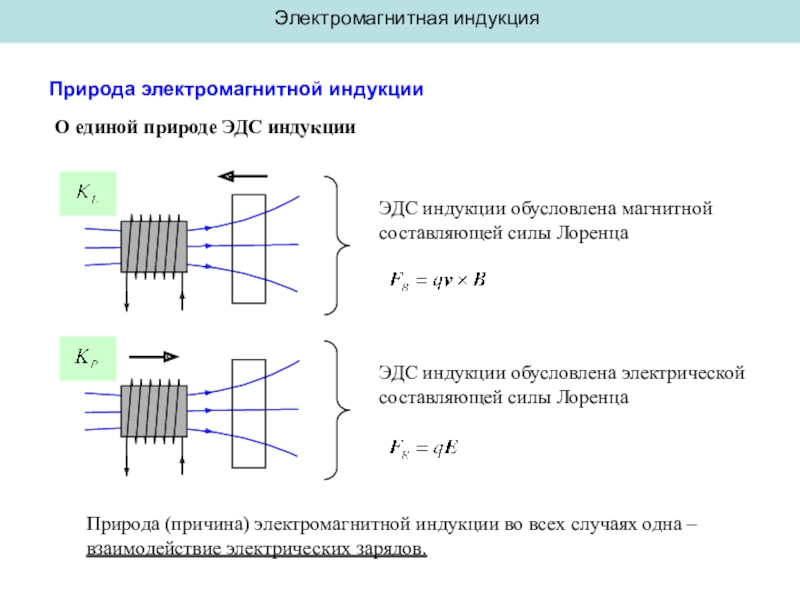
Природа электромагнитной индукции
О единой природе ЭДС индукции
ЭДС индукции обусловлена
магнитной составляющей силы Лоренца
ЭДС индукции обусловлена электрической составляющей силы Лоренца
Природа
(причина) электромагнитной индукции во всех случаях одна –
взаимодействие электрических зарядов.Слайд 18Электромагнитная индукция
Явление самоиндукции
Явление самоиндукции – при изменении тока в контуре
возникает ЭДС (само)индукции в этом же контуре.
Так как
L
– индуктивность контура (L > 0)При изменении тока ЭДС самоиндукции
Слайд 19Электромагнитная индукция
Явление самоиндукции
Индуктивность соленоида
– плотность намотки
– поток через один виток
–
полный поток
Слайд 20Электромагнитная индукция
Взаимная индукция
i
k
Так как
– взаимная индуктивность контуров
(коэффициент взаимной
индукции)
Благодаря взаимной индукции контуры электрически связанны между собой.
Теорема взаимности:
Слайд 21Электромагнитная индукция
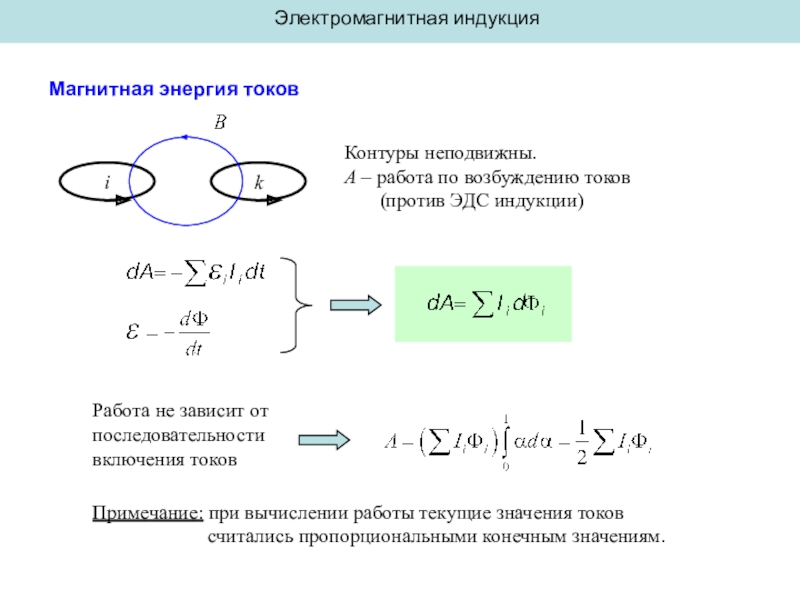
Магнитная энергия токов
i
k
Контуры неподвижны.
A – работа по возбуждению токов
(против ЭДС индукции)
Работа не зависит от последовательности
включения токовПримечание: при вычислении работы текущие значения токов
считались пропорциональными конечным значениям.
Слайд 22Электромагнитная индукция
Магнитная энергия токов
Таким образом
. . . . . .
Соленоид:
w
– объемная плотность
энергии магнитного поля
Слайд 23Электромагнитная индукция
Энергетический метод определения сил
Система токов в вакууме (все сопротивления
= 0)
а) Ф = const
– (обобщенная) сила магнитного
взаимодействия
–
(обобщенная) координата– работа обобщенной силы
По закону сохранения энергии: