Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая логика в задании №18 (ЕГЭ)
Содержание
- 1. Математическая логика в задании №18 (ЕГЭ)
- 2. Основные понятия математической логики в задании №18&Дел>,
- 3. ДизъюнкцияОтрицаниеКонъюнкцияАлгоритм решенияВведение&Дел>,
- 4. Алгоритм решенияВведение&Дел>,
- 5. Алгоритм решенияВведение&Дел>,
- 6. Алгоритм решенияВведение&Дел>,
- 7. Алгоритм решенияВведение&Дел>,
- 8. Задание с битовыми операциямиВведение&Дел>,
- 9. Задание с битовыми операциямиВведение&Дел>,
- 10. Задание с битовыми операциямиВведение&Дел>,
- 11. Задания на делимостьВведение&Дел>,
- 12. Задания на делимостьВведение&Дел>,
- 13. Задания на делимостьВведение&Дел>,
- 14. Задания на делимостьВведение&Дел>,
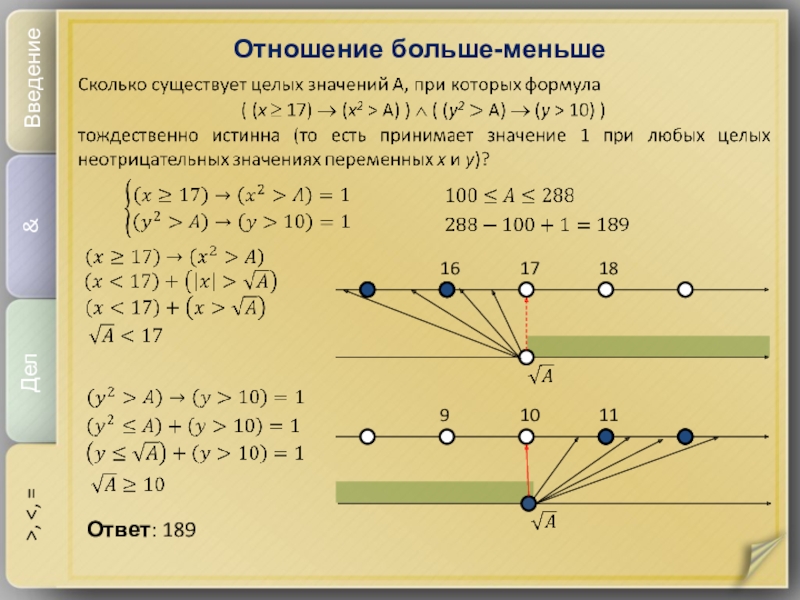
- 15. Отношение больше-меньшеВведение&Дел>,
- 16. Список литературыhttps://vk.com/club180658320Е.А. Мирончик. Метод отображения — видимая часть
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Дизъюнкция
Отрицание
Конъюнкция
Алгоритм решения
Введение
&
Дел
>,
Упростить выражение (Не ЛОЖЬ = ИСТИНА)
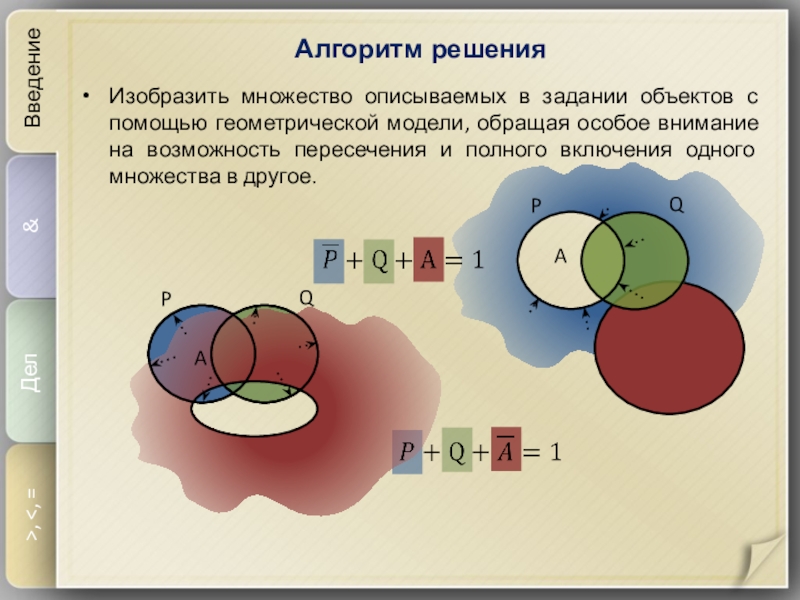
Слайд 4Алгоритм решения
Введение
&
Дел
>,
помощью геометрической модели, обращая особое внимание на возможность пересечения и
полного включения одного множества в другое.P
Q
P
Q
A
A
Слайд 5Алгоритм решения
Введение
&
Дел
>,
операции через простые.
В двоичном представлении числа x есть единица
в четвертом разряде.В двоичном представлении числа x есть хотя бы одна единица, совпадающая с единицами числа 6.
ДЕЛ(x, 2)
Число x кратно 2
ДЕЛ(x, 4)
Число x кратно 4
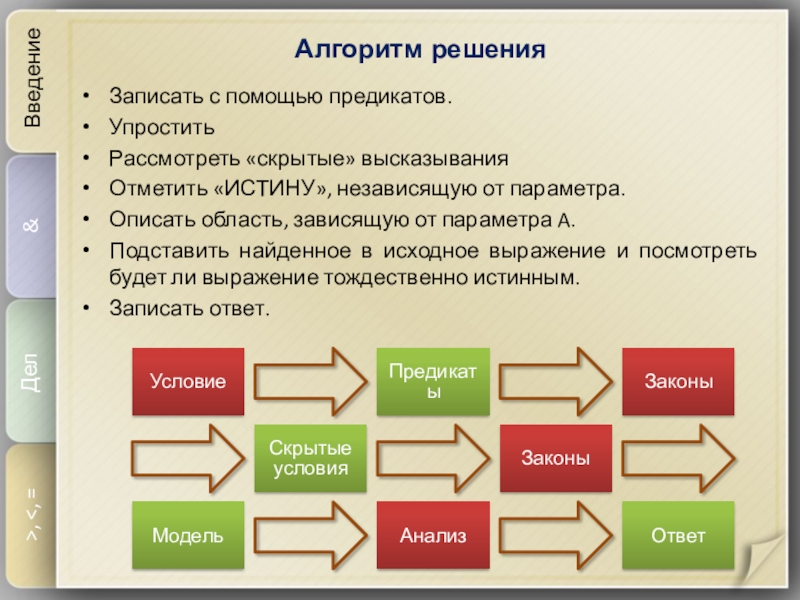
Слайд 6Алгоритм решения
Введение
&
Дел
>,
помощью геометрической модели, обращая особое внимание на возможность пересечения и
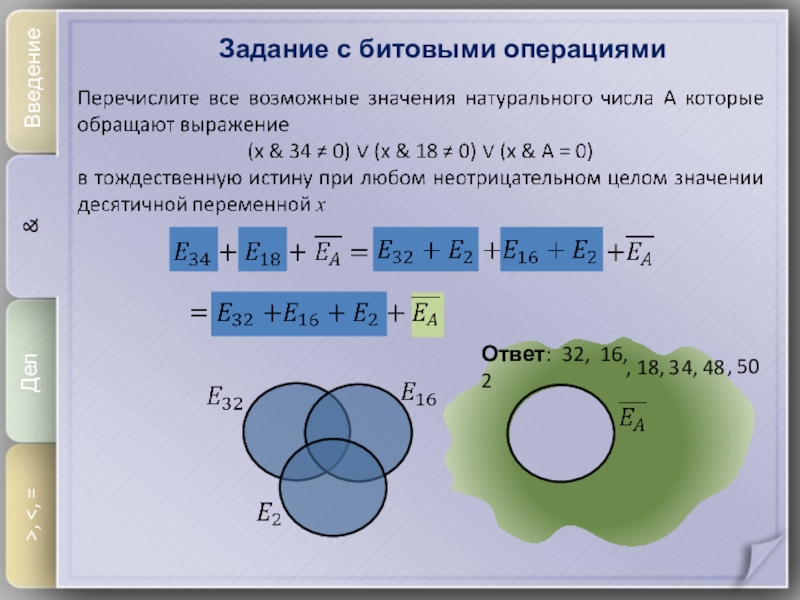
полного включения одного множества в другое.Слайд 7Алгоритм решения
Введение
&
Дел
>,
независящую от параметра.
Описать область, зависящую от параметра A.
Подставить найденное в
исходное выражение и посмотреть будет ли выражение тождественно истинным. Записать ответ.
Слайд 11Задания на делимость
Введение
&
Дел
>,
взаимно простых чисел, то оно делится и на их произведение.
Если
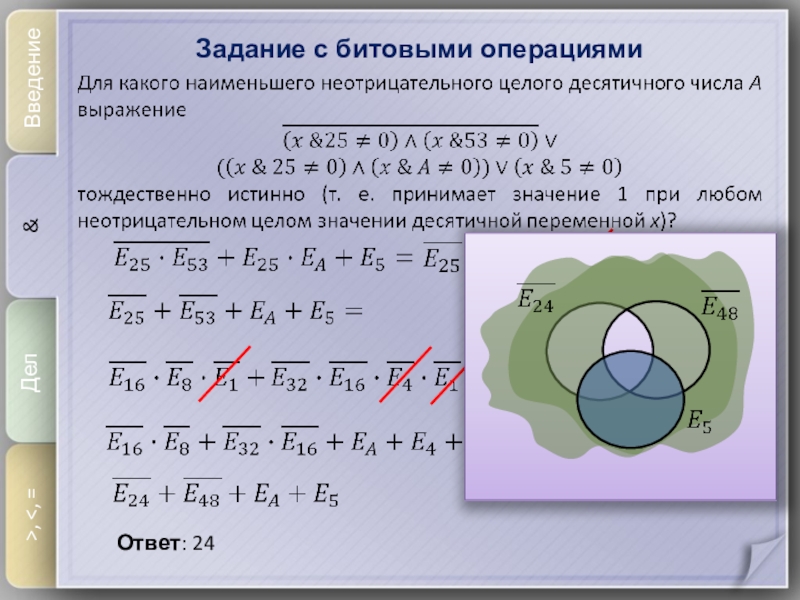
число делится на произведение взаимно простых чисел, то оно делится и на каждое из них. Слайд 12Задания на делимость
Введение
&
Дел
>,
число n делится без остатка на натуральное число m». Для
какого наименьшего натурального числа А формула(ДЕЛ(x, 15) ¬ДЕЛ(x, 21)) (¬ДЕЛ(x, A) ¬ДЕЛ(x, 15))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 7
Слайд 13Задания на делимость
Введение
&
Дел
>,
число n делится без остатка на натуральное число m». Для
какого наибольшего натурального числа А формула(ДЕЛ(x, 40) ДЕЛ(x, 32)) ДЕЛ(x, A)
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 8
Слайд 14Задания на делимость
Введение
&
Дел
>,
число n делится без остатка на натуральное число m». Для
какого наименьшего натурального числа А формулаДЕЛ(x, 2520) ¬ДЕЛ(x, 5940) (¬ДЕЛ(x, A)
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 56
Слайд 16Список литературы
https://vk.com/club180658320
Е.А. Мирончик. Метод отображения — видимая часть айсберга // Информатика, № 10,
2019, с. 43-52.
Е.А. Мирончик. Графы и системы логических уравнений // Информатика, № 8, 2016,
с. 35-39.Е.А. Мирончик. Люблю ЕГЭ за B15, или Ещё раз про метод отображения // Информатика, № 8, 2014, с. 26-32.
Е.А. Мирончик. Метод отображения // Информатика, № 10, 2013, с. 18-26.
Е.А. Мирончик. Алгебра предикатов и построение геометрических моделей на ЕГЭ по информатике // Информатика, № 3, 2019, с. 40-47.