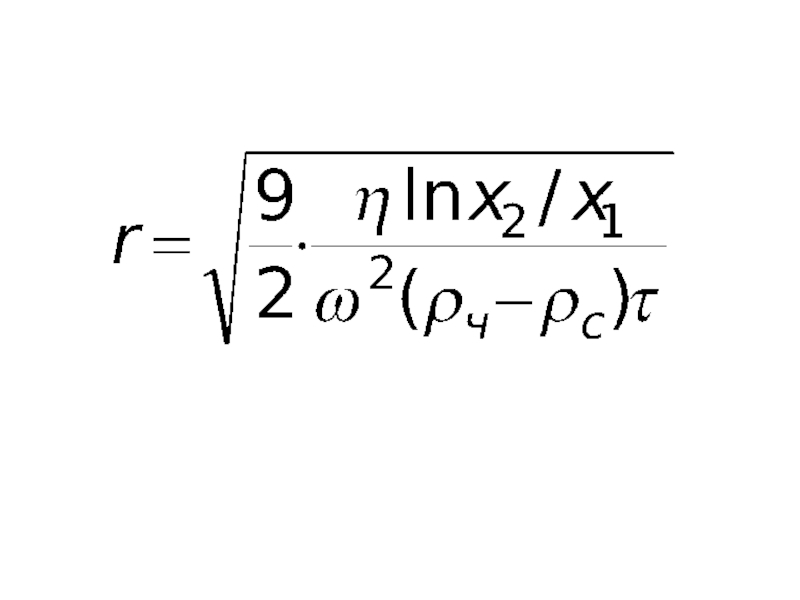Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
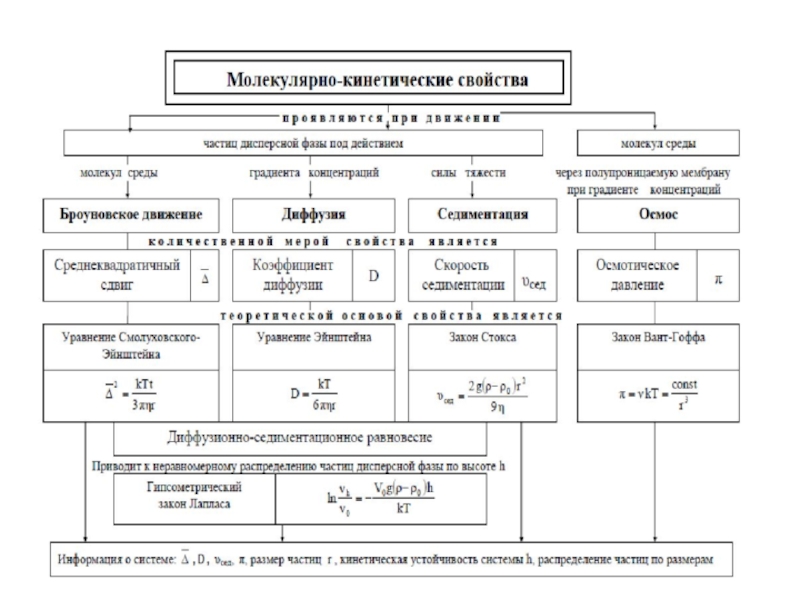
Молекулярно-кинетические свойства дисперсных систем
Содержание
- 1. Молекулярно-кинетические свойства дисперсных систем
- 2. Коллоидные частицы по размерам занимают промежуточное положение
- 3. Ро́берт Бро́ун (англ. Robert Brown, 1773—1858) — британский (шотландский) ботаник конца
- 4. Броуновское движение – непрерывное беспорядочное
- 5. Броуновское движение можно наблюдать при помощи микроскопа.
- 6. В результате хаотического движения
- 7. Диффузия описывается первым законом Фика коэффициент диффузии
- 8. Слайд 8
- 9. Молекулярно-кинетические свойства коллоидов …Диффузия ‒ самопроизвольный процесс
- 10. Слайд 10
- 11. Теория броуновского движения была разработана А.Эйнштейном и
- 12. Мариан Смолуховский (1872–1917) Впервые в 1904 году дал строгое объяснение броуновского движения
- 13. Альберт Эйнштейн (1879-1955) В 1905 году создал
- 14. Альберт Эйнштейн (1879 ‒ 1955)
- 15. Слайд 15
- 16. По уравнению Эйнштейна - Смолуховского зная размеры
- 17. Слайд 17
- 18. Слайд 18
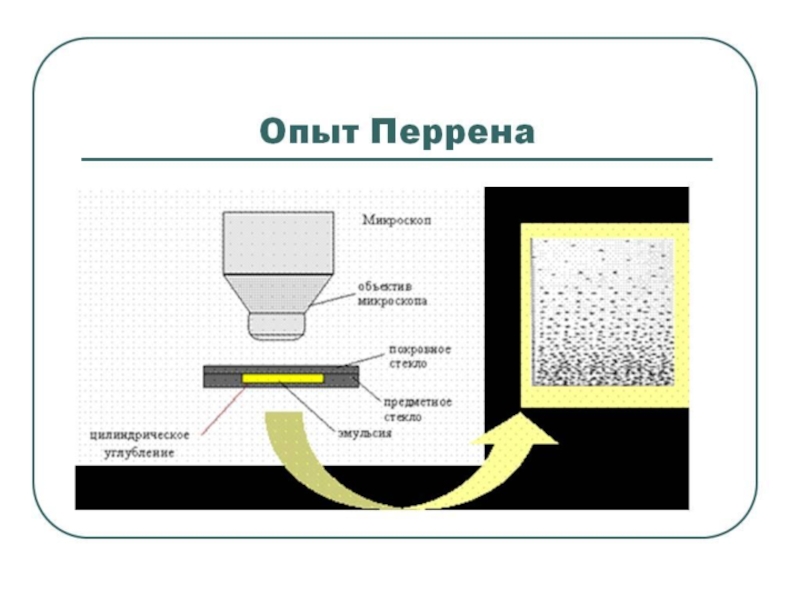
- 19. Жан Батист Перрен (1870 - 1942) В
- 20. Рисунки траекторий броуновских частиц из книги Ж. Перрена «Атомы», опубликованной в 1920 г. в Париже
- 21. Слайд 21
- 22. Слайд 22
- 23. Участие частиц дисперсной фазы в броуновском движении
- 24. Слайд 24
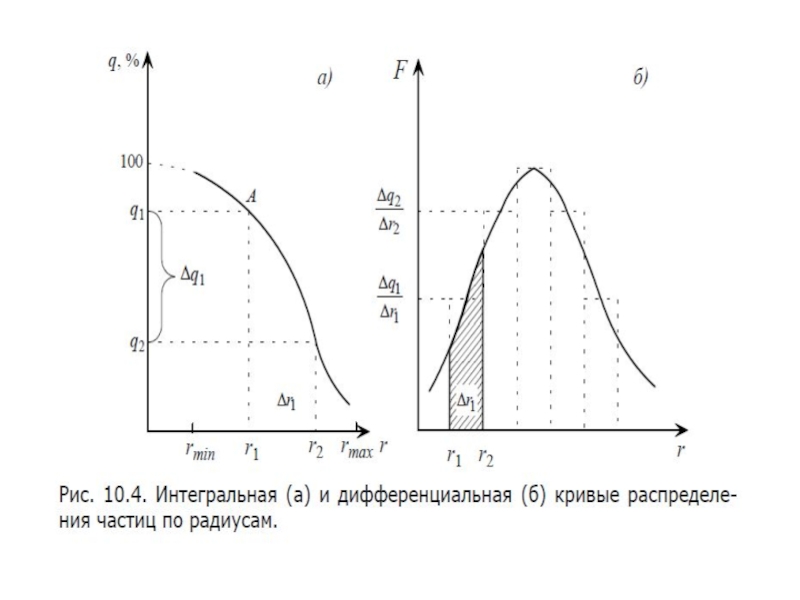
- 25. Распределение броуновских частиц в слоях на разной высоте
- 26. Распределение частиц при равновесии в монодисперсной системе
- 27. Слайд 27
- 28. Коллоидные растворы золота полученные Майклом Фарадеем
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
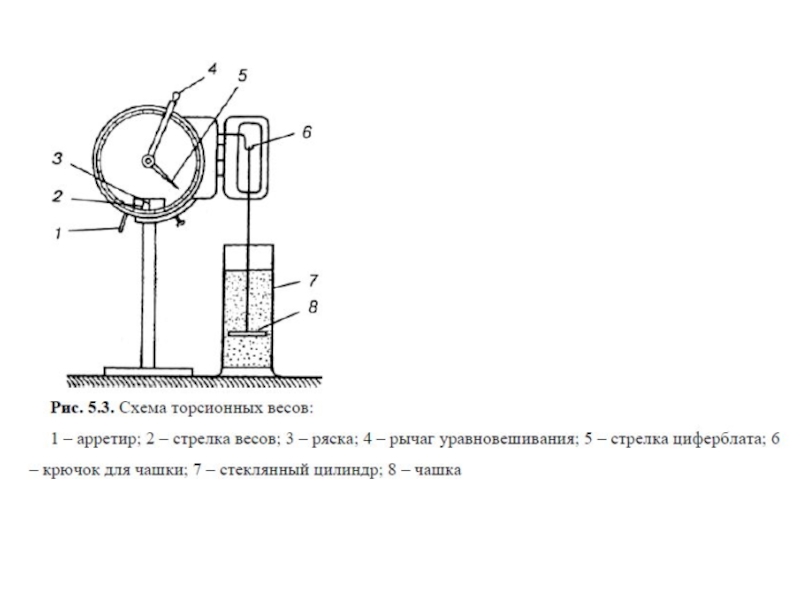
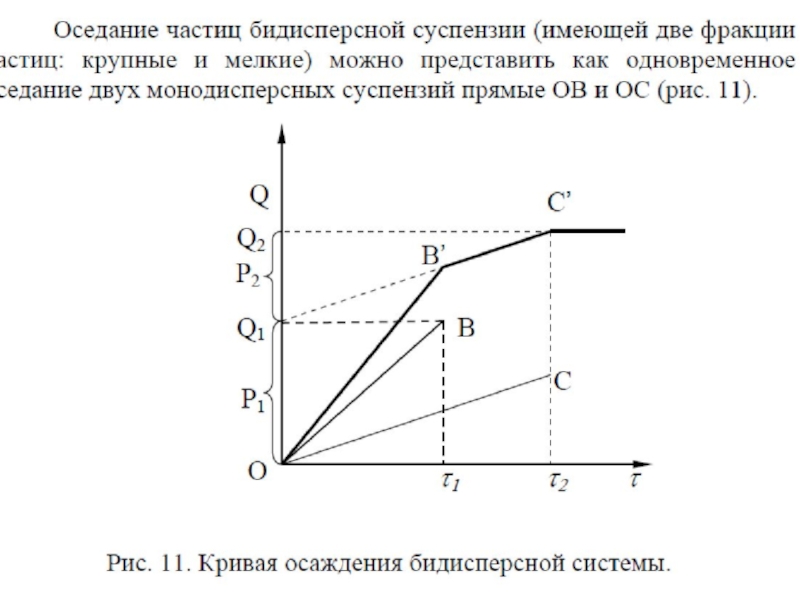
- 42. В 1923 г. Т.Сведберг и Г Ринде
- 43. Слайд 43
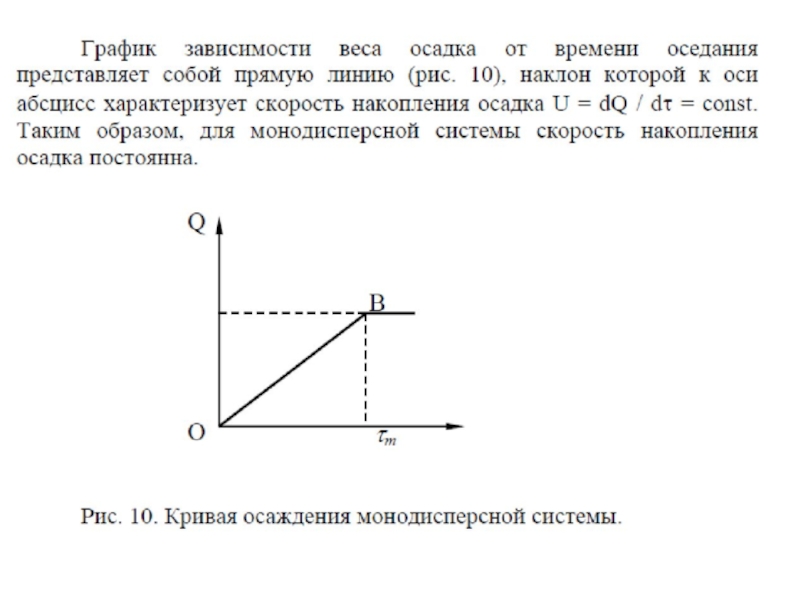
- 44. Время оседания в центробежном поле рассчитывается по формуле:Скорость оседания:
- 45. Слайд 45
- 46. С точки зрения термодинамики осмос обусловлен ростом
- 47. Молекулярно-кинетические свойства коллоидов …Осмос ‒ самопроизвольный процесс
- 48. Слайд 48
- 49. В коллоидных растворах также должно наблюдаться явление
- 50. Величина аналогичная молярной массе в истинных растворах
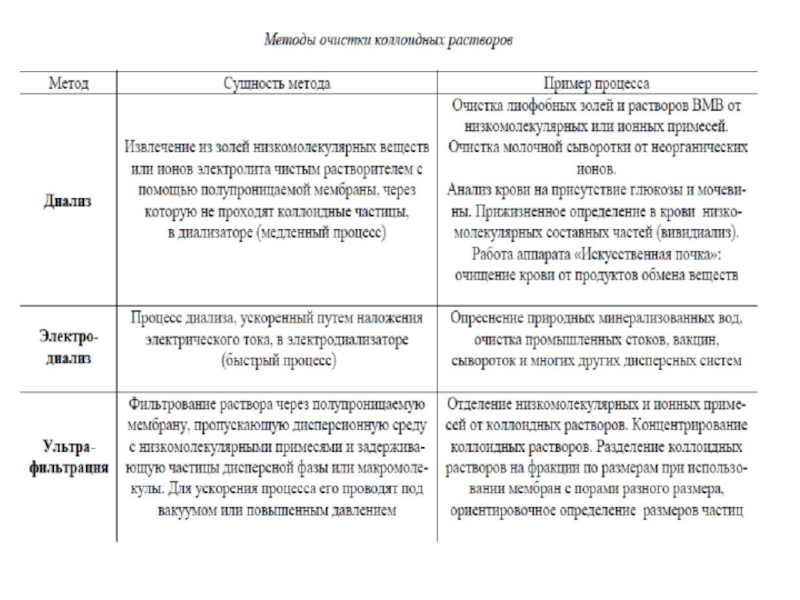
- 51. Некоторые молекулярно-кинетические свойства коллоидных систем используют для
- 52. Слайд 52
- 53. Слайд 53
- 54. Слайд 54
- 55. Слайд 55
- 56. Скачать презентанцию
Коллоидные частицы по размерам занимают промежуточное положение между грубодисперсными частицами и молекулами. Они доступны для наблюдения, и в то же время настолько малы, что участвуют в тепловом
Слайды и текст этой презентации
Слайд 2 Коллоидные частицы по размерам занимают промежуточное положение между грубодисперсными частицами
и молекулами.
наблюдения, и в то же время настолько малы, что участвуют в тепловом движении. Для них справедливо основное положение молекулярно-кинетической теории:
Слайд 3Ро́берт Бро́ун (англ. Robert Brown, 1773—1858) — британский (шотландский) ботаник конца XVIII — первой половины
XIX века, морфолог и систематик растений, первооткрыватель «броуновского движения»
В 1827 году Броун обнаружил с помощью микроскопа движение мелких частиц - спор папоротника, взвешенных в воде. Более крупные частицы находились в колебательном движении.Колебания и перемещения частиц ускорялись с уменьшением размера частиц, повышением температуры и не были связаны с какими-либо внешними условиями.
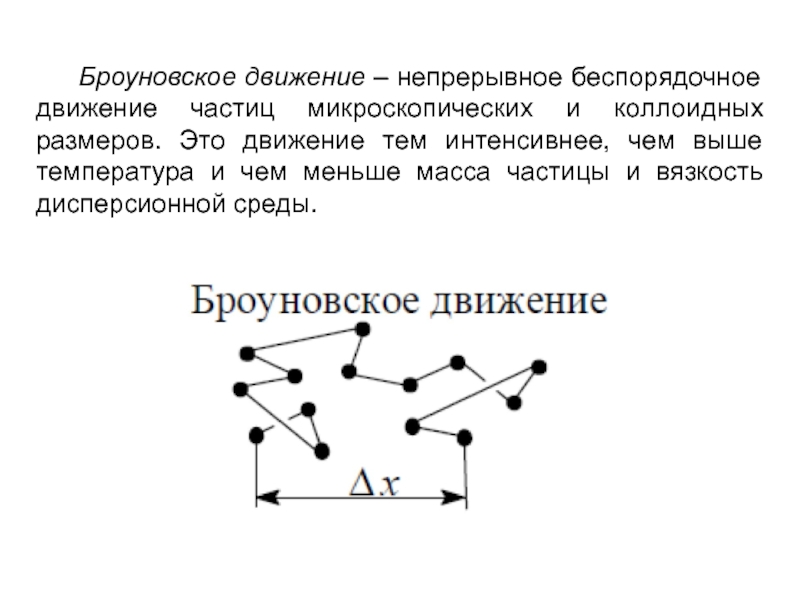
Слайд 4 Броуновское движение – непрерывное беспорядочное движение частиц микроскопических
и коллоидных размеров. Это движение тем интенсивнее, чем выше температура
и чем меньше масса частицы и вязкость дисперсионной среды.
Слайд 5Броуновское движение можно наблюдать при помощи микроскопа. Частица перемещается из-за
различного числа одновременных ударов неодинаковой силы молекулами дисперсионной среды
Слайд 6 В результате хаотического движения частиц дисперсной фазы
наблюдается диффузия (от лат diffusio – распространение) (выравнивание их концентраций
в разных частях системы), приводящая к тому при различных концентрациях возникает поток вещества из области с большей концентрацией в область с меньшей.Диффузия происходит самопроиз-вольно так как сопровождается увели-чением энтропии системы
Слайд 9Молекулярно-кинетические свойства коллоидов …
Диффузия ‒ самопроизвольный процесс выравнивания концентрации частиц
за счёт их теплового движения.
1-й закон Фика: скорость диффузии прямо
пропорциональна площади, через которую происходит диффузия, и градиенту концентрацииС
S
X
t = 0
t
dm/dt ‒ масса вещества, продиффундировавшего за ∞ малое время через площадь S;
dc/dx ‒ градиент концентрации или падение концентрации на ∞ малом отрезке х.
Слайд 11Теория броуновского движения была разработана А.Эйнштейном и М.Смолуховским. Первая работа
Эйнштейна посвященная количественной теории броуновского движения "О движении взвешенных в
покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты" была опубликована в 17 томе Анналов физики за 1905 г. В этом же томе были опубликованы еще две основополагающие статьи Эйнштейна посвященные квантовой теории фотоэффекта и теории относительности.Выдающийся немецкий физик Макс Борн назвал этот том "одной из самых замечательных книг в научной литературе. Она содержит три статьи Эйнштейна, каждая из которых имеет дело с различным предметом, и каждая является сегодня признанным шедевром, началом новой области физики". Остается добавить, что Эйнштейну в это время было 26 лет.
Слайд 12Мариан Смолуховский (1872–1917)
Впервые в 1904 году дал строгое объяснение броуновского
движения
Слайд 13Альберт Эйнштейн
(1879-1955)
В 1905 году создал
первую количественную теорию броуновского
движения.
С помощью статистических методов он вывел формулу для среднего значения
квадрата смещения броуновской частицы:где B - подвижность частицы, которая
обратно пропорциональна вязкости среды и размеру частицы,
t – время наблюдения, Т – температура жидкости.
< r 2 > = 6kTBt
Слайд 16 По уравнению Эйнштейна - Смолуховского зная размеры частицы и экспериментально
определив величину среднего сдвига можно рассчитать постоянную Больцмана или число
Авогадро
Слайд 19
Жан Батист Перрен
(1870 - 1942)
В 1906 году начал проводить опыты,
подтвердившие теорию Эйнштейна.
Подводя итоги в 1912 году, он заявил:
«Атомная теория восторжествовала. Некогда многочисленные, её противники повержены и один за другим отрекаются от своих взглядов, в течение столь долгого времени считавшихся обоснованными и полезными». В 1926 г. Перрен получил Нобелевскую премию
за работу по «дискретной природе материи»
Слайд 20Рисунки траекторий броуновских частиц из книги Ж. Перрена «Атомы», опубликованной в 1920 г.
в Париже
Слайд 23Участие частиц дисперсной фазы в броуновском движении отражается на их
седиментационной способности. При оседании частиц в гравитационном поле увеличивается их
концентрация в нижних слоях, в результате чего возникает диффузионный поток частиц из области с большей концетрацией в область с меньшей концентрационной плотностью частиц. Этот поток направлен вверх противоположно седиментационному потоку. Если частицы достаточно малы (10-7 – 10-9м) то может наступить диффузионно-седиментационное равновесие, которое характеризуется постоянным во времени распределением числа частиц в единице объема вдоль столба дисперсионной среды. Наибольшая концентрация частиц на дне сосуда наименьшая в верхней части.Именно диффузионно-седиментационным равновесием объясняется устойчивость многих коллоидных растворов.
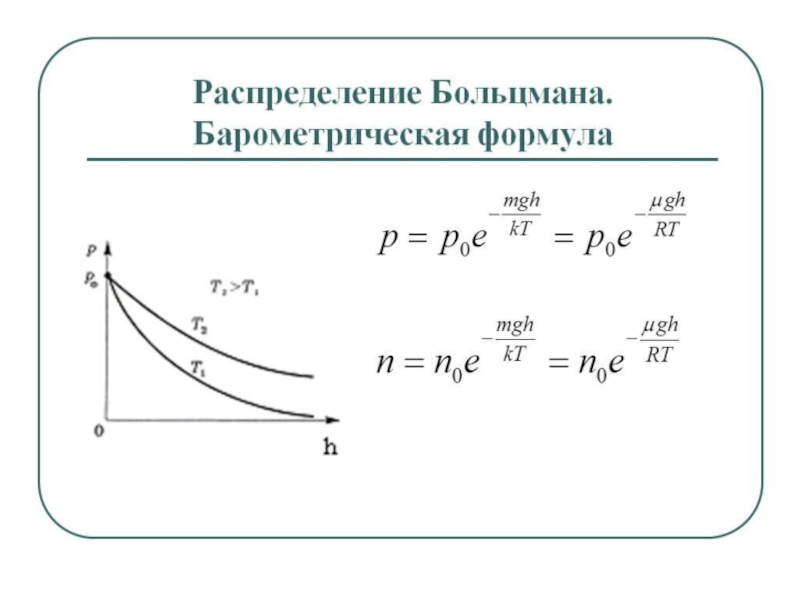
Слайд 26Распределение частиц при равновесии в монодисперсной системе описывается гипсометрической формулой
– уравнением Лапласа – Перрена
или в экспоненциальной форме
Слайд 41
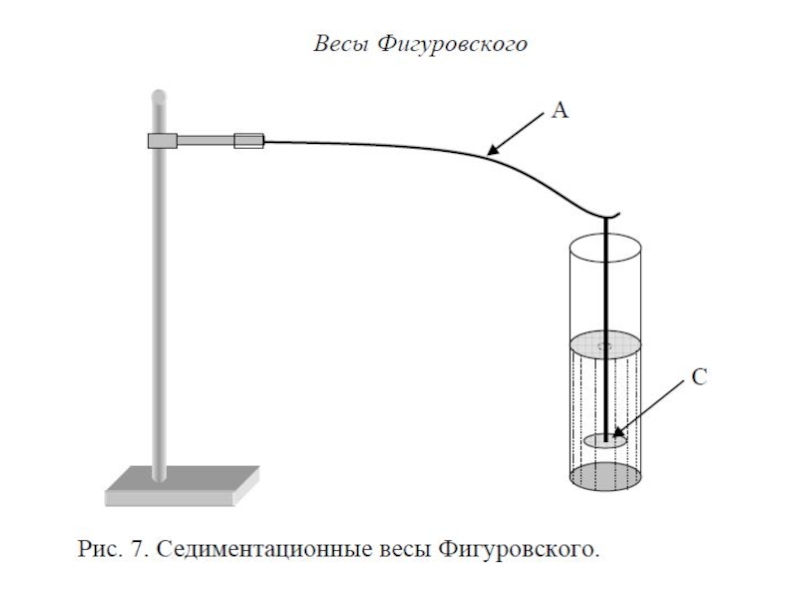
Ультрацентрифуга
Под действием силы тяжести оседают только
крупные частицы. Коллоидные частицы оседают чрезвычайно медленно. Так, частицы кварца (r=110-7 м) проходят путь в 1 см за 86 ч. Поэтому для ускорения седиментации заменяют гравитационное поле центробежным, применяя ультрацентрифуги, дающие мощное силовое поле. Ускорения, создаваемые ультрацентрифугой, достигают 105 g, а число оборотов - 75 тыс. об/мин. При таких ускорениях та же частица кварца проходит путь в 1 см за 3 с.
Слайд 42В 1923 г. Т.Сведберг и Г Ринде сконструировали ультрацентрифугу для
проведения анализа золей. Эта центрифуга, делая 10000 оборотов в минуту,
создавала ускорение превышающее ускорение силы тяжести в 5000 раз.Метод ультрацентрифугирования позволил выделять высокодисперсные частицы, измерять их массы, а также молекулярные массы макромолекул полимеров.
Радиус сферической частицы, оседающей в центробежном поле, определяют по формуле
Слайд 46 С точки зрения термодинамики осмос обусловлен ростом энтропии при смешении
растворов. С кинетической точки зрения тем, что со стороны раствора
с меньшей концентрацией в мембрану ударяет и проходит через нее большее число молекул растворителя чем со стороны раствора с большей концентрацией.Для уравновешивания этого потока к раствору с большей концентрацией необходимо приложить дополнительное давление.
Слайд 47Молекулярно-кинетические свойства коллоидов …
Осмос ‒ самопроизвольный процесс перехода растворителя через
мембрану из раствора с меньшей концентрацией в раствор с большей,
в результате чего возникает осмотическое давление.π = сdRT ‒ закон Вант-Гоффа.
сd ‒ частичная концентрация.
Слайд 49В коллоидных растворах также должно наблюдаться явление осмоса.
Рассмотрим можно ли
применять в этом случае уравнение Вант – Гоффа. Для этвета
на этот вопрос необходимо уточнить, что можно считать концентрацией дисперсной фазы в дисперсных системах.Введем понятие концентрационной плотности частиц дисперсной фазы
.
Слайд 50Величина аналогичная молярной массе в истинных растворах (масса 1 моля
частиц) для коллоидных растворов будет вычисляться по формуле:
Значения
Значениия
М очень велики, по сравнению с молярной массой истинных растворов. Они имеют порядок 107 г/моль.
Слайд 51Некоторые молекулярно-кинетические свойства коллоидных систем используют для очистки золей от
электролитов и молекулярных примесей, которыми полученные золи часто бывают загрязнены.
Наиболее распространенными методами очистки коллоидных систем являются диализ, электродиализ и ультрафильтрация, основанные на свойстве некоторых материалов – т.н. полупроницаемых мембран (коллодия, пергамента, целлофана и т.п.) – пропускать ионы и молекулы небольших размеров и задерживать коллоидные частицы.
