Математические методы и модели в экономике

Содержание

1. Математические методы и модели в экономике
2. Сложности моделирования в экономикеСложность объекта моделирования;Многокритериальность практических задач;Человеческий фактор.
3. Этапы построения моделиПредварительный анализ объекта;Формулировка (построение) задачи;Построение модели;Нахождение численного решения;Анализ модели на чувствительность.
4. Пример 1Фабрика производит краску: I – для
5. Слайд 5
6. Задача следующего вида:
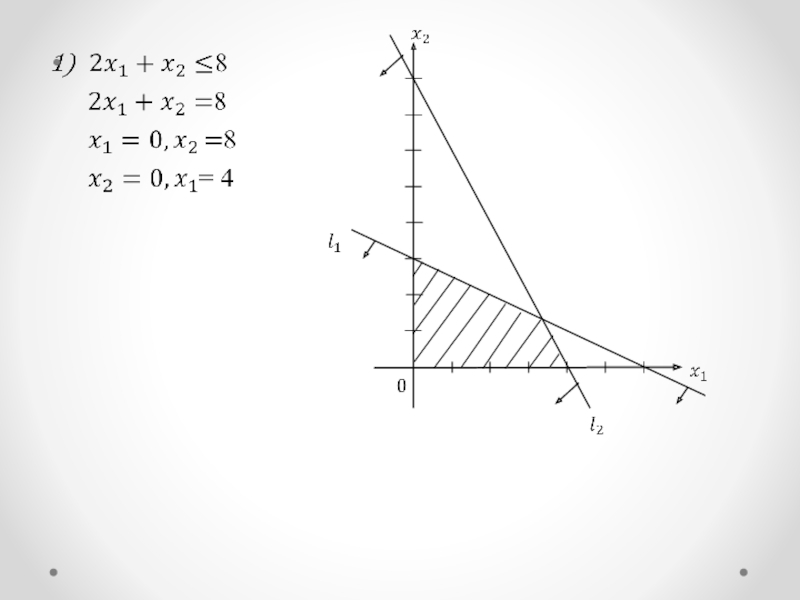
7. Графическое решение задачи ЛП
8. Слайд 8
9. CDFAEBОбласть допустимых решений
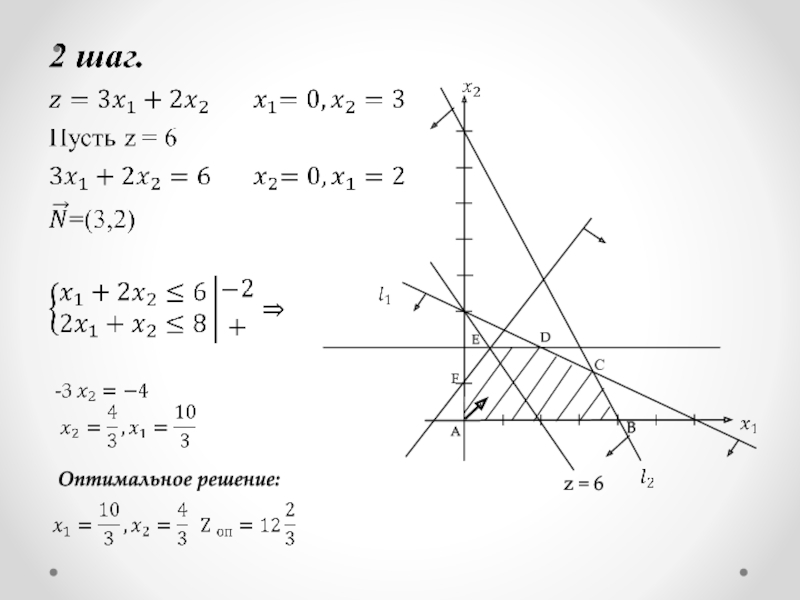
10. CDFAz = 6EОптимальное решение:B
11. Опр. Множество точек называется выпуклым, если для
12. Слайд 12
13. Стандартная форма задачи ЛПВ стандартной форме задачи
14. Слайд 14
15. Слайд 15
16. Слайд 16
17. Слайд 17
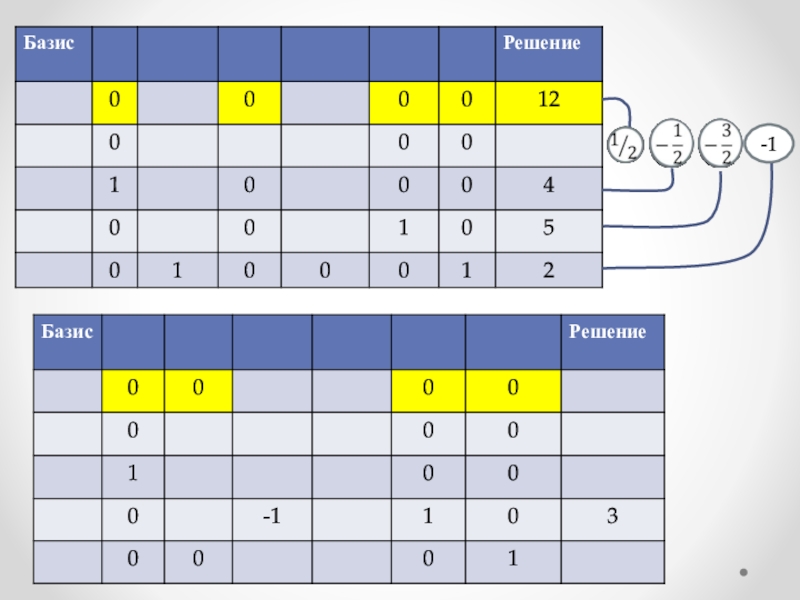
18. Шаг 3. Находим базисное решение используя метод
19. 3-11
20. -1
21. Скачать презентанцию

Сложности моделирования в экономикеСложность объекта моделирования;Многокритериальность практических задач;Человеческий фактор.

Главная
Разное
Математические методы и модели в экономике

Слайды и текст этой презентации

Слайд 1Математические методы и модели в экономике
Доктор экономических наук, профессор
Шмидт Юрий

Давыдович

Слайд 2Сложности моделирования в экономике
Сложность объекта моделирования;
Многокритериальность практических задач;
Человеческий фактор.

Сложности моделирования в экономикеСложность объекта моделирования;Многокритериальность практических задач;Человеческий фактор.

Слайд 3Этапы построения модели
Предварительный анализ объекта;
Формулировка (построение) задачи;
Построение модели;
Нахождение численного решения;
Анализ

модели на чувствительность.

Этапы построения моделиПредварительный анализ объекта;Формулировка (построение) задачи;Построение модели;Нахождение численного решения;Анализ модели на чувствительность.

Слайд 4Пример 1
Фабрика производит краску: I – для наружных работ, II

– для внутренних работ.

Расходы исходных продуктов А и В представлены

в таблице

Дополнительные условия рынка: суточный спрос на краску II никогда не превышает спроса на краску I, более чем на 1 т. Кроме того, спрос на краску II никогда не превышает 2 т в сутки.
Какое количество краски каждого вида должна производить фабрика, чтобы прибыль была максимальной?

Пример 1Фабрика производит краску: I – для наружных работ, II – для внутренних работ.Расходы исходных продуктов А

Слайд 5

Слайд 6Задача следующего вида:

Слайд 7Графическое решение задачи ЛП

Слайд 8

Слайд 9C
D
F
A
E
B
Область допустимых решений

Слайд 10C
D
F
A
z = 6
E
Оптимальное решение:
B

Слайд 11Опр. Множество точек называется выпуклым, если для любых двух точек

этого множества отрезок, соединяющий эти точки, полностью принадлежит множеству.

Теор 1.

Множество всех допустимых решений системы ограничений задачи ЛП является выпуклым.

Теор 2. Если существует оптимальное
решение задачи ЛП то оно достигается
в угловой точке множества допустимых
решений.

Теоретические основы симплекс-метода (алгебраический метод) решения задачи ЛП

Опр. Множество точек называется выпуклым, если для любых двух точек этого множества отрезок, соединяющий эти точки, полностью

Слайд 12

Слайд 13Стандартная форма задачи ЛП
В стандартной форме задачи ЛП:
все ограничения записываются

в виде равенств с неотрицательной правой частью;
значения всех переменных неотрицательны;
целевая

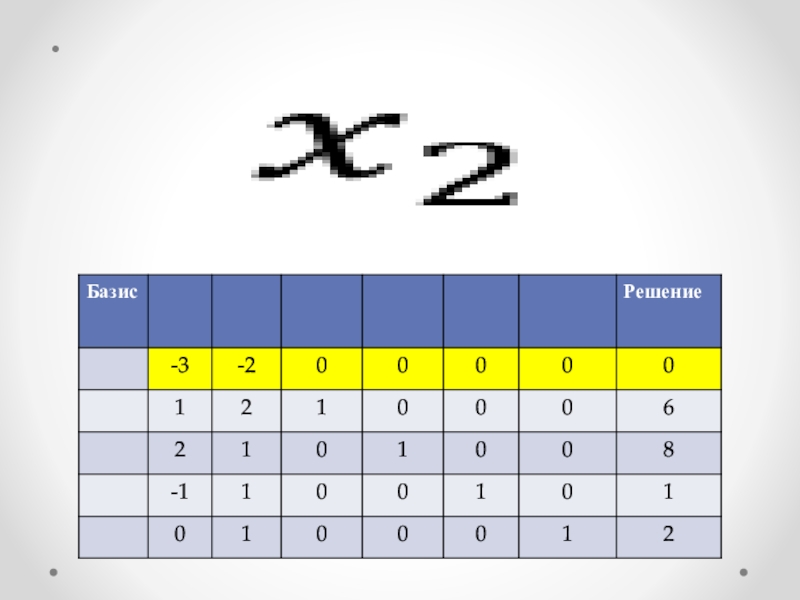
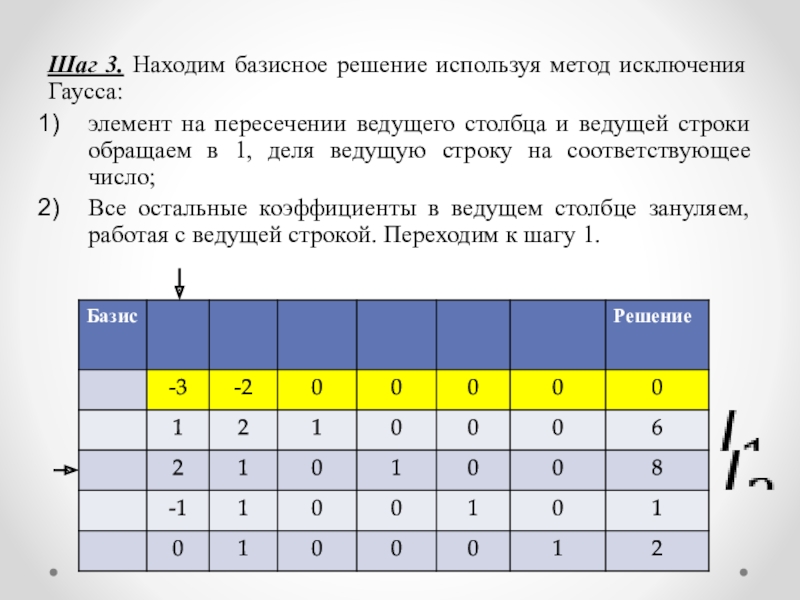
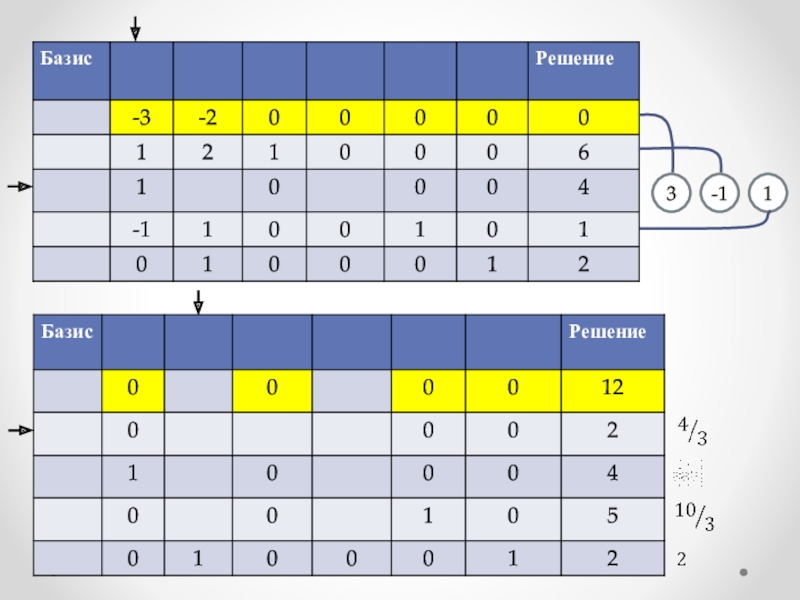
функция подлежит максимизации.

Стандартная форма задачи ЛПВ стандартной форме задачи ЛП:все ограничения записываются в виде равенств с неотрицательной правой частью;значения

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18Шаг 3. Находим базисное решение используя метод исключения Гаусса:
элемент на

пересечении ведущего столбца и ведущей строки обращаем в 1, деля

ведущую строку на соответствующее число;
Все остальные коэффициенты в ведущем столбце зануляем, работая с ведущей строкой. Переходим к шагу 1.

Шаг 3. Находим базисное решение используя метод исключения Гаусса:элемент на пересечении ведущего столбца и ведущей строки обращаем

Слайд 193
-1
1

Слайд 20-1

Скачать презентацию

Разделы презентаций

Математические методы и модели в экономике

Содержание

Слайды и текст этой презентации

Слайд 1Математические методы и модели в экономике
Доктор экономических наук, профессор
Шмидт Юрий

Давыдович

Слайд 2Сложности моделирования в экономике
Сложность объекта моделирования;
Многокритериальность практических задач;
Человеческий фактор.

Слайд 3Этапы построения модели
Предварительный анализ объекта;
Формулировка (построение) задачи;
Построение модели;
Нахождение численного решения;
Анализ

модели на чувствительность.

Слайд 4Пример 1
Фабрика производит краску: I – для наружных работ, II

– для внутренних работ.

Расходы исходных продуктов А и В представлены

Слайд 5

Слайд 6Задача следующего вида:

Слайд 7Графическое решение задачи ЛП

Слайд 8

Слайд 9C
D
F
A
E
B
Область допустимых решений

Слайд 10C
D
F
A
z = 6
E
Оптимальное решение:
B

Слайд 11Опр. Множество точек называется выпуклым, если для любых двух точек

этого множества отрезок, соединяющий эти точки, полностью принадлежит множеству.

Теор 1.

Слайд 12

Слайд 13Стандартная форма задачи ЛП
В стандартной форме задачи ЛП:
все ограничения записываются

в виде равенств с неотрицательной правой частью;
значения всех переменных неотрицательны;
целевая

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18Шаг 3. Находим базисное решение используя метод исключения Гаусса:
элемент на

пересечении ведущего столбца и ведущей строки обращаем в 1, деля

Слайд 193
-1
1

Слайд 20-1

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Математические методы и модели в экономике

Содержание

Слайды и текст этой презентации

Слайд 1Математические методы и модели в экономикеДоктор экономических наук, профессорШмидт Юрий

Давыдович

Слайд 2Сложности моделирования в экономикеСложность объекта моделирования;Многокритериальность практических задач;Человеческий фактор.

Слайд 3Этапы построения моделиПредварительный анализ объекта;Формулировка (построение) задачи;Построение модели;Нахождение численного решения;Анализ

модели на чувствительность.

Слайд 4Пример 1Фабрика производит краску: I – для наружных работ, II

– для внутренних работ.Расходы исходных продуктов А и В представлены

Слайд 5

Слайд 6Задача следующего вида:

Слайд 7Графическое решение задачи ЛП

Слайд 8

Слайд 9CDFAEBОбласть допустимых решений

Слайд 10CDFAz = 6EОптимальное решение:B

Слайд 11Опр. Множество точек называется выпуклым, если для любых двух точек

этого множества отрезок, соединяющий эти точки, полностью принадлежит множеству.Теор 1.

Слайд 12

Слайд 13Стандартная форма задачи ЛПВ стандартной форме задачи ЛП:все ограничения записываются

в виде равенств с неотрицательной правой частью;значения всех переменных неотрицательны;целевая

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18Шаг 3. Находим базисное решение используя метод исключения Гаусса:элемент на

пересечении ведущего столбца и ведущей строки обращаем в 1, деля

Слайд 193-11

Слайд 20-1

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Математические методы и модели в экономике
Доктор экономических наук, профессор
Шмидт Юрий

Слайд 2Сложности моделирования в экономике
Сложность объекта моделирования;
Многокритериальность практических задач;
Человеческий фактор.

Слайд 3Этапы построения модели
Предварительный анализ объекта;
Формулировка (построение) задачи;
Построение модели;
Нахождение численного решения;
Анализ

Слайд 4Пример 1
Фабрика производит краску: I – для наружных работ, II

– для внутренних работ.

Расходы исходных продуктов А и В представлены

Слайд 9C
D
F
A
E
B
Область допустимых решений

Слайд 10C
D
F
A
z = 6
E
Оптимальное решение:
B

этого множества отрезок, соединяющий эти точки, полностью принадлежит множеству.

Теор 1.

Слайд 13Стандартная форма задачи ЛП
В стандартной форме задачи ЛП:
все ограничения записываются

в виде равенств с неотрицательной правой частью;
значения всех переменных неотрицательны;
целевая

Слайд 18Шаг 3. Находим базисное решение используя метод исключения Гаусса:
элемент на

Слайд 193
-1
1