Математические методы. Оптимизация на графах

Методы теории графов находят широкое применение в экономике, в частности,

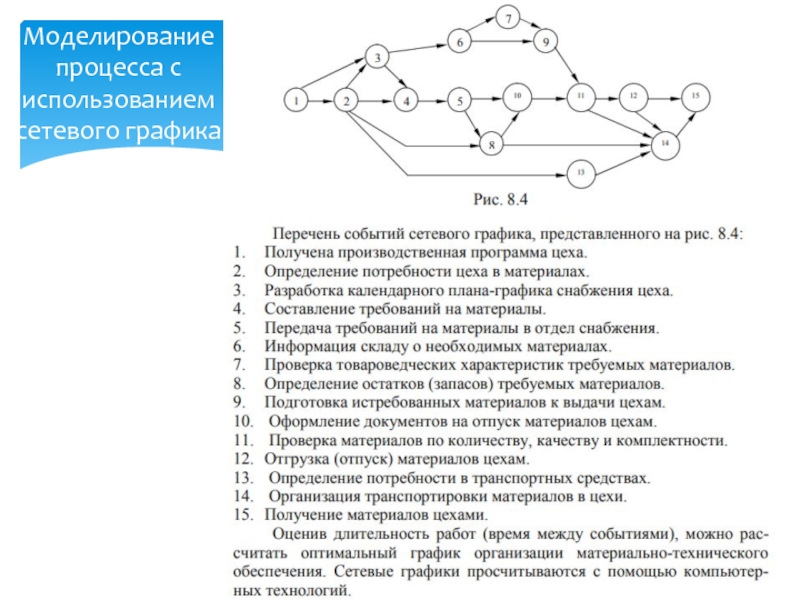
в виде системы сетевого планирования и управления.
При помощи сетевого планирования и управления достигается рациональное использование материальных ресурсов, осуществляется надежное и ритмичное материально-техническое обеспечение.

Графы для принятия решений

дуги графа.
На рисунке представлен фрагмент сетевого графика с указанием

основных параметров.

Пример

находящихся на критическом пути, ранние сроки равны поздним, а поэтому

отсутствует резерв.
Длительность критического пути определяет длительность всего процесса.
На основании рассчитанного сетевого графика составляется план-график поставок – материальные ресурсы должны быть поставлены в период между ранними и поздними сроками данного события, т. е. к началу следующей работы.

Выводы по анализу

В таблице приведены длительности переправы в каждый порт. Требуется построить

сетевой график, определить ранние и поздние сроки событий, а также критический путь в соответствии с данными, указанными в таблице.

Самостоятельный расчет

называемый топологический анализ, или анализ связности, оперирующий понятиями комплекса, симплекса;

q – связности и экцентрисета.
Этот анализ определяет связность подсистем в системе.
Симплициальный комплекс – обобщение понятия планарного графа,
отражающее многомерную природу рассматриваемого бинарного отношения между элементами системы. В общем виде систему можно представить в виде множества пар элементов, связанных некоторым отношением R.
Тип отношения может быть различным: соответствие, подобие, сходство, различие и т.п.:
S = {( x, y ) : x ∈ X , y ∈ Y , xRy}.

Методы изучения структуры систем

информации о том, как каждый отдельный симплекс входит в комплекс.

Для оценки степени интегрированности каждого симплекса в структуре всего комплекса используют понятие эксцентриситета.

Эксцентриситет

2) ЕСС является мерой гибкости вершин к изменениям в системе.та