Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические неожиданности «Софизм» и «Парадокс»
Содержание
- 1. Математические неожиданности «Софизм» и «Парадокс»
- 2. Цель:Найти математические задачи, приводящие к парадоксам.Исследовать решение
- 3. Задачи: дать определение понятием «софизм» и «парадокс»
- 4. Методы исследования:Сбор информации, обработка данных, наблюдение, сравнение, анализ, обобщение.
- 5. «Софизм» и «Парадокс»
- 6. СофизмЛожное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным.
- 7. ПарадоксЭто нечто необычное и удивительное, то, что расходится с привычными ожиданиями, здравым смыслом и жизненным опытом.
- 8. Их отличие С софизмом их различает то, что парадокс - не преднамеренно полученный противоречивый результат.
- 9. Классификация математических неожиданностейАлгебраические Геометрические Арифметические Логические
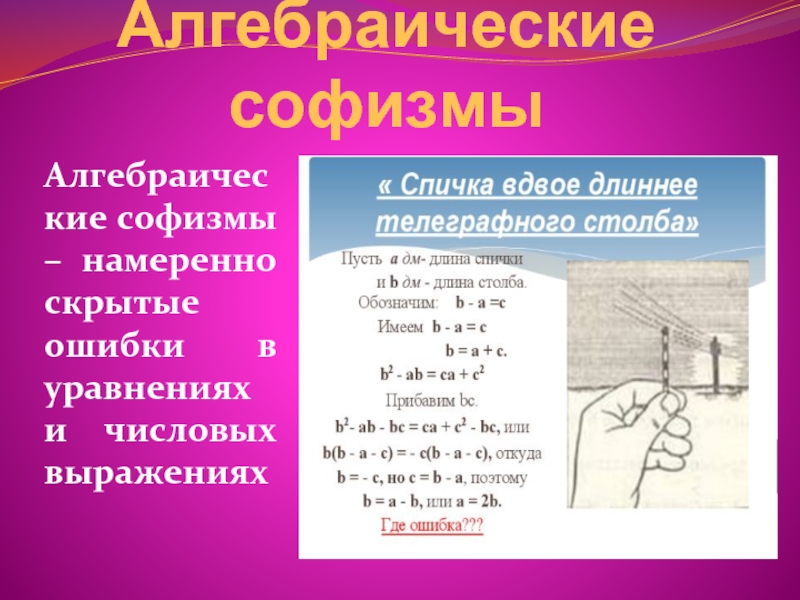
- 10. Алгебраические софизмыАлгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях
- 11. Арифметические софизмыАрифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
- 12. Геометрические софизмыГеометрические софизмы – это умозаключения, обосновывающие какую-нибудь заведомую нелепость, связанную с геометрическими фигурами ми.
- 13. Логичесике софизмыЧем больше учишься, тем больше знаешь.Чем
- 14. Многообразие парадоксов
- 15. Парадокс парикмахера В одной деревне жил единственный парикмахер-мужчина.
- 16. Основные типы геометрических парадоксов
- 17. Невозможный треугольник
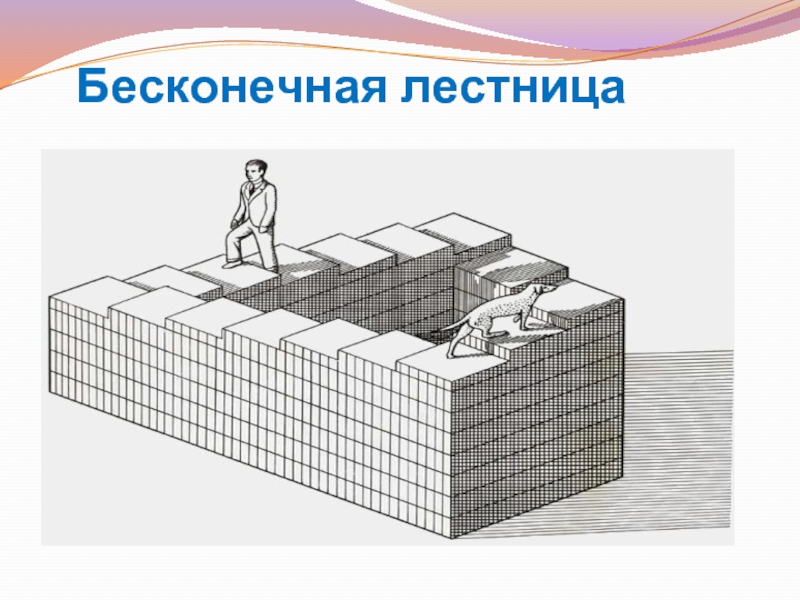
- 18. Бесконечная лестница
- 19. Космическая вилка
- 20. Сумасшедший ящик
- 21. Имп-Арт - искусство парадоксальных картин
- 22. Имп-Арт - искусство парадоксальных картин
- 23. Имп-Арт - искусство парадоксальных картин
- 24. Выводы:Итак, в процессе работы:я узнала, что называется
- 25. Спасибо за внимание!
- 26. Скачать презентанцию
Цель:Найти математические задачи, приводящие к парадоксам.Исследовать решение этих задач.Найти, где скрыты ошибки, подготовить презентацию по этой теме для использования на уроках математики.
Слайды и текст этой презентации
Слайд 2Цель:
Найти математические задачи, приводящие к парадоксам.
Исследовать решение этих задач.
Найти, где
Слайд 3Задачи:
дать определение понятием «софизм» и «парадокс» , узнать ,в
чем их отличие;
классифицировать математические неожиданности;
научиться находить ошибки в готовых
решениях, математических задач;
подготовить презентацию .
Слайд 4Методы исследования:
Сбор информации, обработка данных, наблюдение, сравнение, анализ, обобщение.
Слайд 6Софизм
Ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется
правильным.
Слайд 7Парадокс
Это нечто необычное и удивительное, то, что расходится с привычными
ожиданиями, здравым смыслом и жизненным опытом.
Слайд 8Их отличие
С софизмом их различает то, что парадокс -
не преднамеренно полученный противоречивый результат.
Слайд 9Классификация математических неожиданностей
Алгебраические
Геометрические
Арифметические
Логические
Слайд 10Алгебраические софизмы
Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и
числовых выражениях
Слайд 11Арифметические софизмы
Арифметические софизмы – это числовые выражения, имеющие неточность или
ошибку, не заметную с первого взгляда.
Слайд 12Геометрические софизмы
Геометрические софизмы – это умозаключения, обосновывающие какую-нибудь заведомую нелепость,
связанную с геометрическими фигурами ми.
Слайд 13Логичесике софизмы
Чем больше учишься, тем больше знаешь.
Чем больше знаешь, тем
больше забываешь.
Чем больше забываешь, тем меньше знаешь.
Чем меньше знаешь, тем
меньше забываешь.Но чем меньше забываешь, тем больше знаешь.
Так для чего учиться?
Слайд 15Парадокс парикмахера
В одной деревне жил единственный парикмахер-мужчина. Здесь был издан
указ: "Парикмахер имеет право брить тех и только тех жителей
деревни, которые не бреются сами". Спрашивается, может ли парикмахер брить сам себя?Слайд 24Выводы:
Итак, в процессе работы:
я узнала, что называется "софизмом "и "парадоксом",
и в чём их отличия;
проклассифицировала софизмы в соответствии с разделами
математики, к которым они принадлежат;рассмотрела четыре основных вида геометрических парадоксов, которые вызвали у меня особый интерес, так как нашли своё отражение в имп-арт – искусстве парадоксальных картин.
Теги