Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математический анализ
Содержание
- 1. Математический анализ
- 2. Понятие функцииОпределение.Если для каждого значения переменной x,
- 3. Графический способ задания функцииОпределение.Графиком функции
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
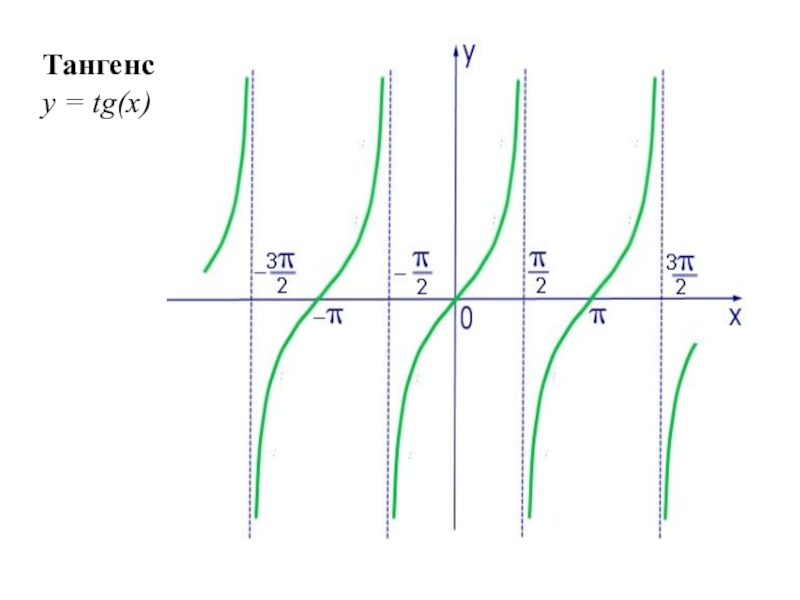
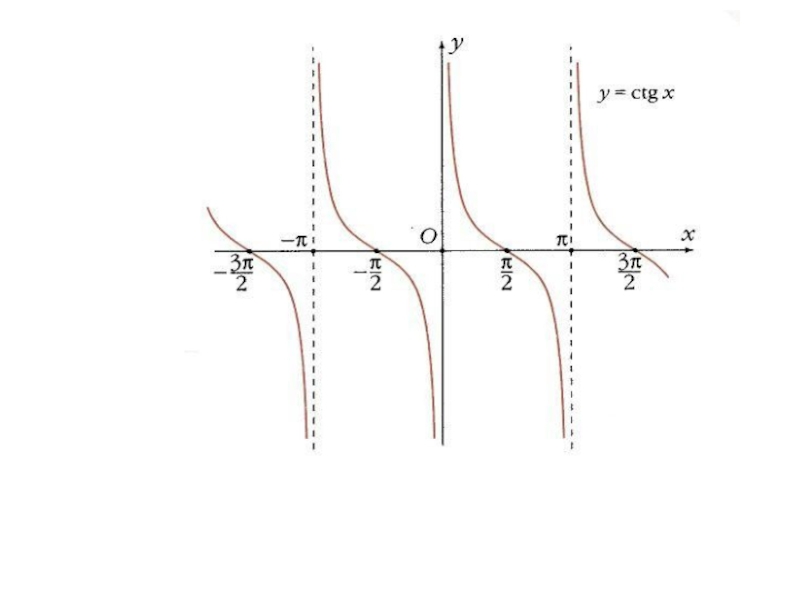
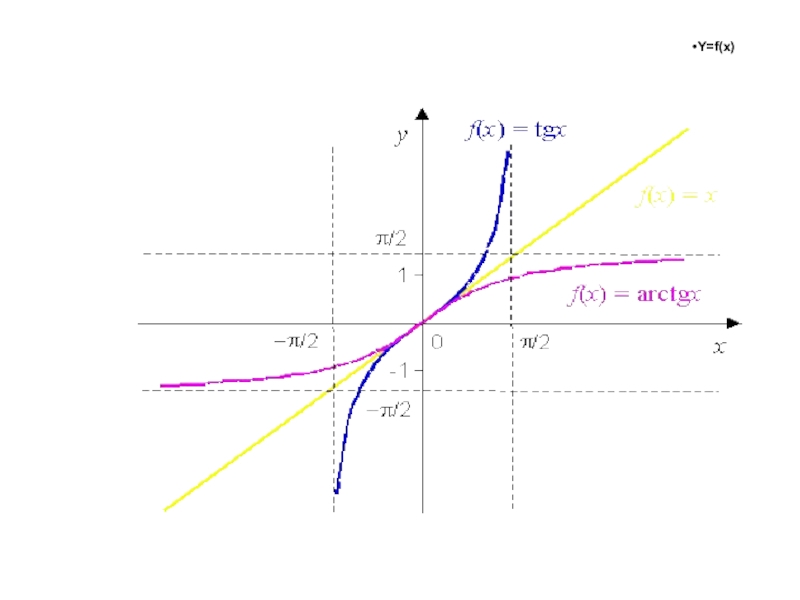
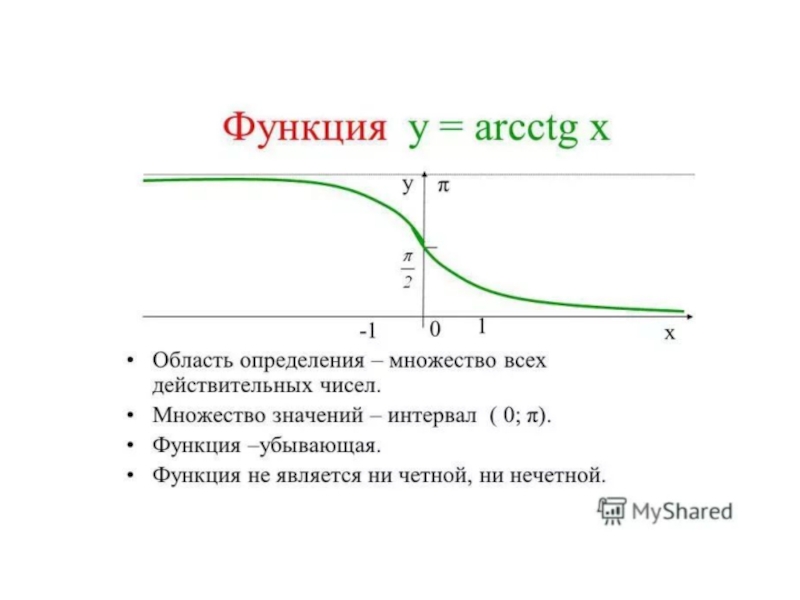
- 26. Тангенсy = tg(x)
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
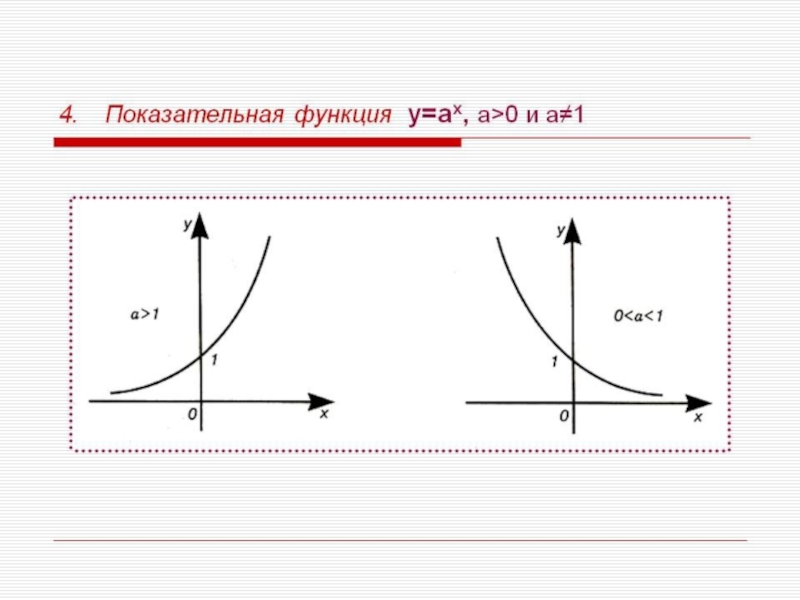
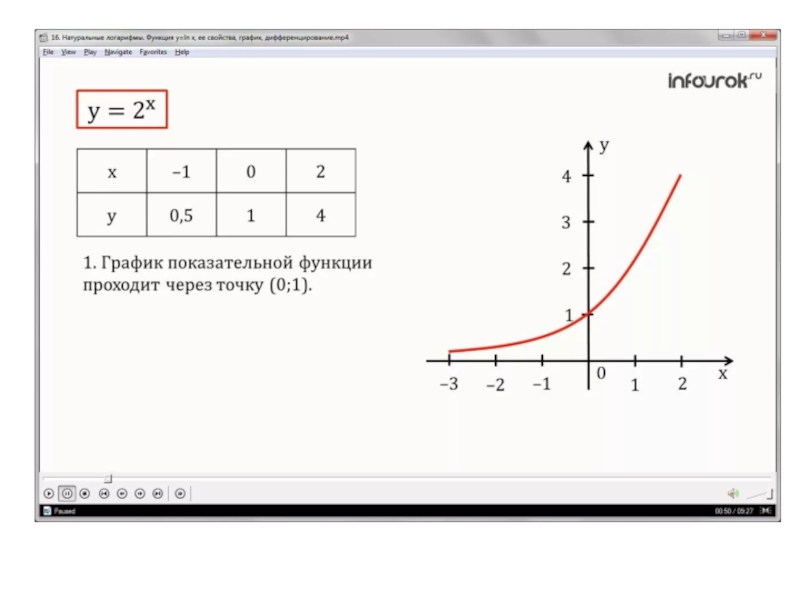
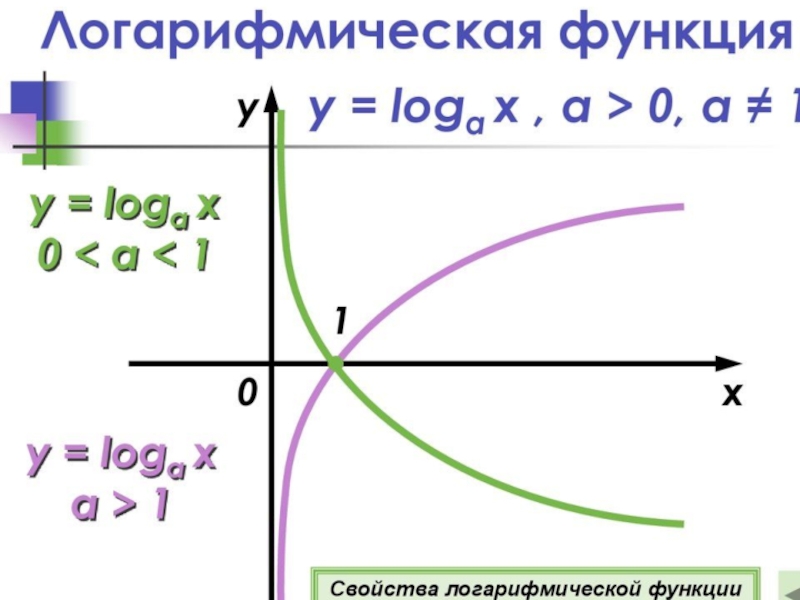
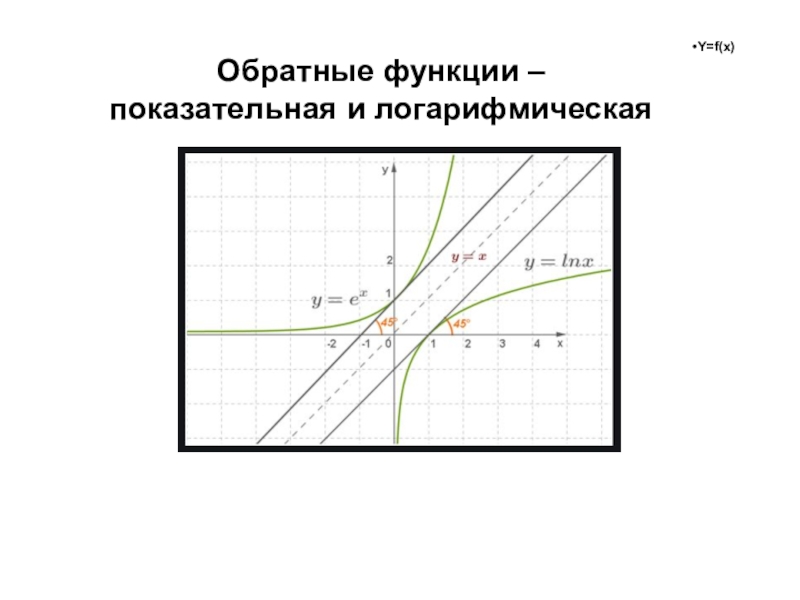
- 31. Обратные функции – показательная и логарифмическая
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
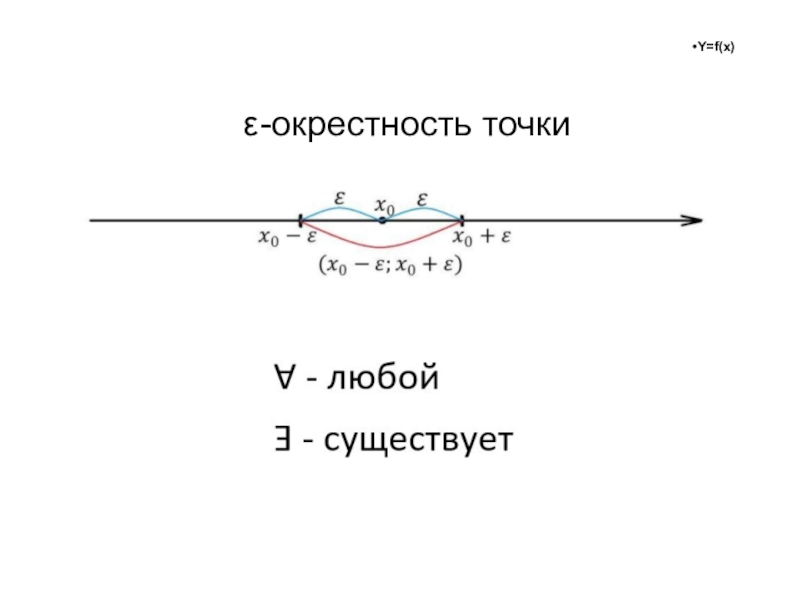
- 38. ε-окрестность точки
- 39. Число b называется пределом функции f(x) при
- 40. Слайд 40
- 41. Предел функции.Пример.хy0121234-1-окрестность-окрестность Для произвольной
- 42. Частный случай предела.Определение.Функция f(x) называется бесконечно малой
- 43. Предел функции на бесконечностиПредел функции приОпределение.Предел функции
- 44.
- 45. Предел функцииОдносторонние пределы.1. Правосторонний предел в точке.Определение.
- 46. Утверждение.1. Если существует
- 47.
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. Слайд 52
- 53. Слайд 53
- 54. Скачать презентанцию
Понятие функцииОпределение.Если для каждого значения переменной x, принадлежащей числовому множеству D по некоторому правилу ( по формуле) задается единственное значение y из числового множества М, то говорят, что задана функция Y=f(x)f
Слайды и текст этой презентации
Слайд 1Математический анализ
Числовые функции и их свойства
Элементарные функции
Предел функции в точке
и на бесконечности
Слайд 2Понятие функции
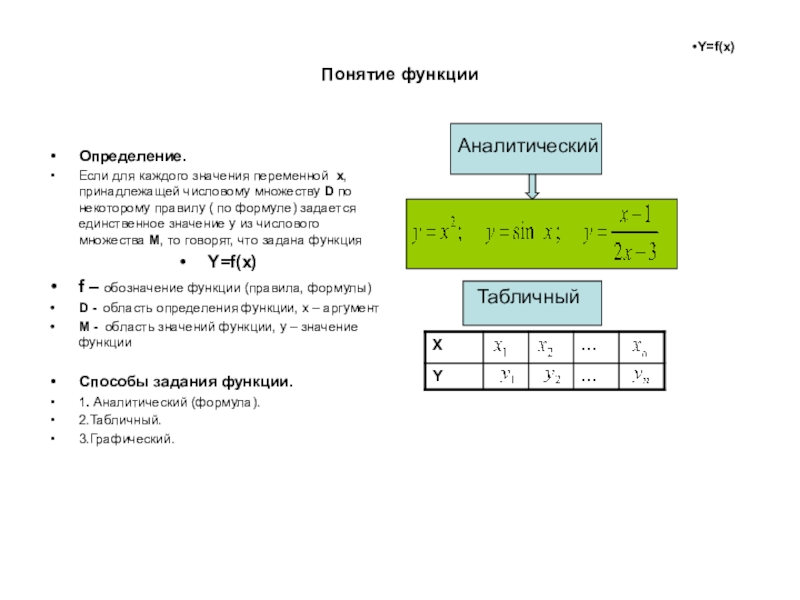
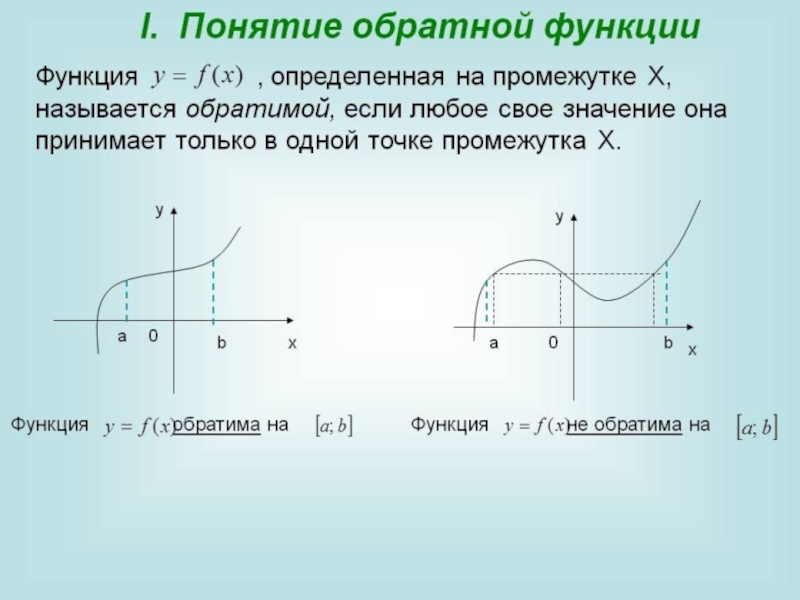
Определение.
Если для каждого значения переменной x, принадлежащей числовому множеству
D по некоторому правилу ( по формуле) задается единственное значение
y из числового множества М, то говорят, что задана функцияY=f(x)
f – обозначение функции (правила, формулы)
D - область определения функции, х – аргумент
М - область значений функции, y – значение функции
Способы задания функции.
1. Аналитический (формула).
2.Табличный.
3.Графический.
Аналитический
Табличный
Слайд 3Графический способ задания функции
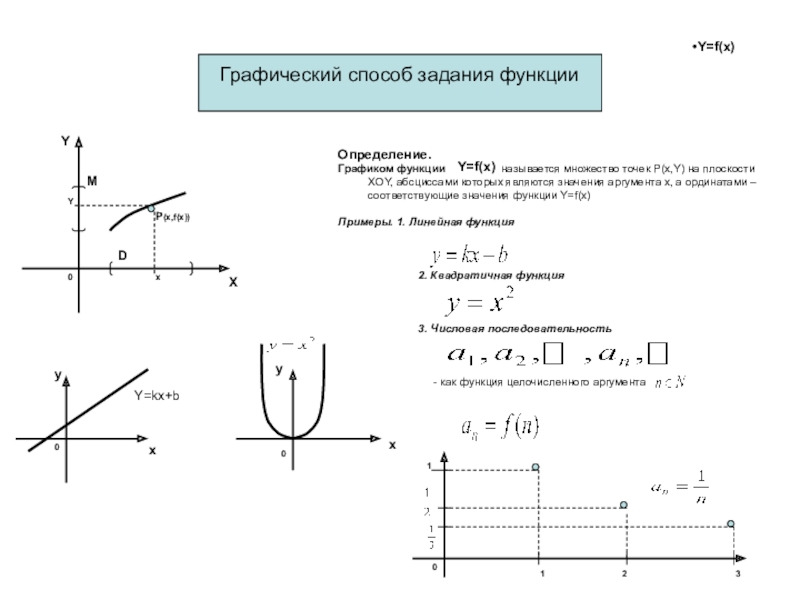
Определение.
Графиком функции
называется множество точек P(x,Y) на плоскости XOY,
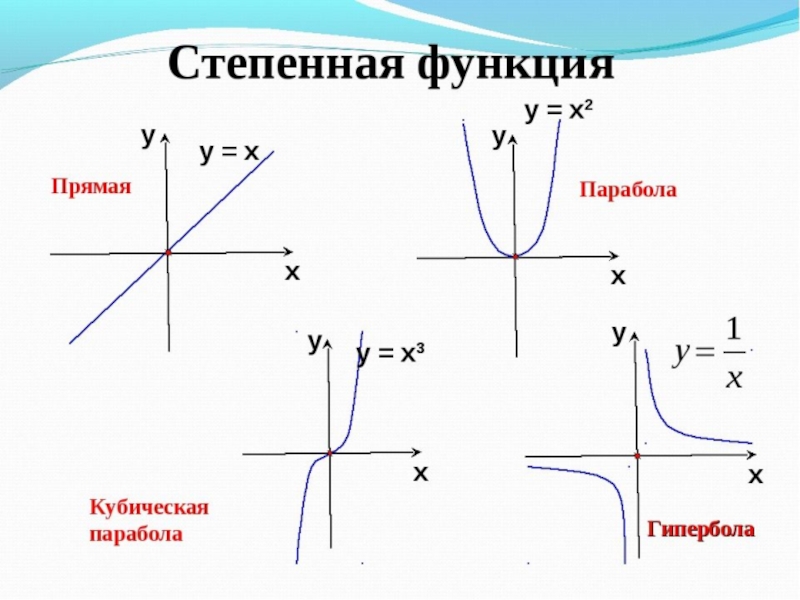
абсциссами которых являются значения аргумента х, а ординатами – соответствующие значения функции Y=f(x)Примеры. 1. Линейная функция
2. Квадратичная функция
3. Числовая последовательность
- как функция целочисленного аргумента
Y=f(x)
0
X
Y
x
Y
P(x,f(x))
0
х
y
Y=kx+b
0
x
y
0
1
2
1
3
D
M
Слайд 39Число b называется пределом функции f(x) при
, если
для любой
-окрестности точки b существует такая -окрестность точки a,
что для всех х из -окрестности
значения будут принадлежать -окрестности.
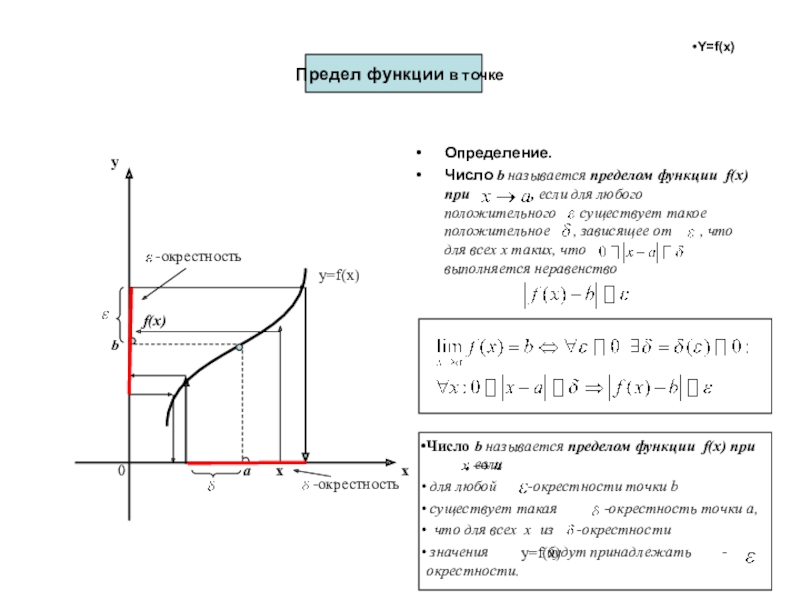
Предел функции в точке
Определение.
Число b называется пределом функции f(x) при , если для любого положительного существует такое положительное , зависящее от , что для всех х таких, что выполняется неравенство
х
y
0
a
b
-окрестность
-окрестность
х
f(x)
y=f(x)
y=f(x)
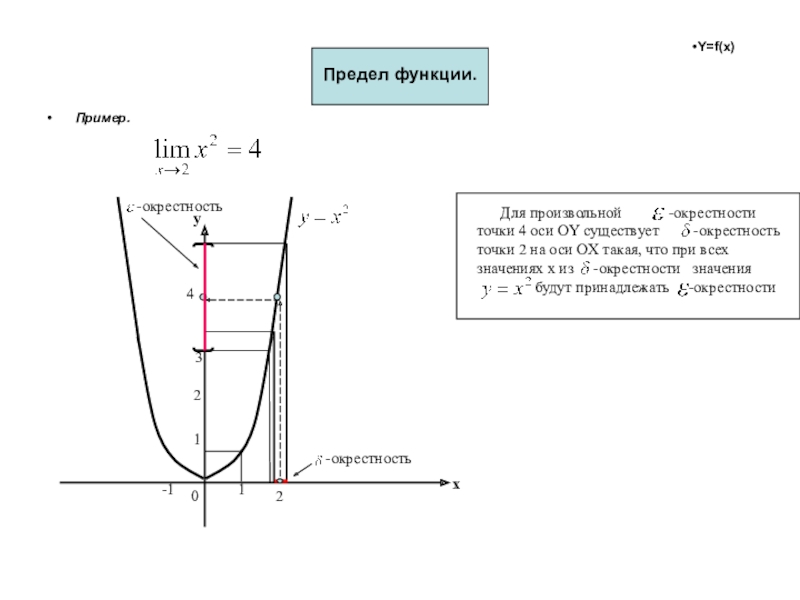
Слайд 41Предел функции.
Пример.
х
y
0
1
2
1
2
3
4
-1
-окрестность
-окрестность
Для произвольной
-окрестности
точки 4 оси OY существует
-окрестностьточки 2 на оси OX такая, что при всех
значениях х из -окрестности значения
будут принадлежать -окрестности
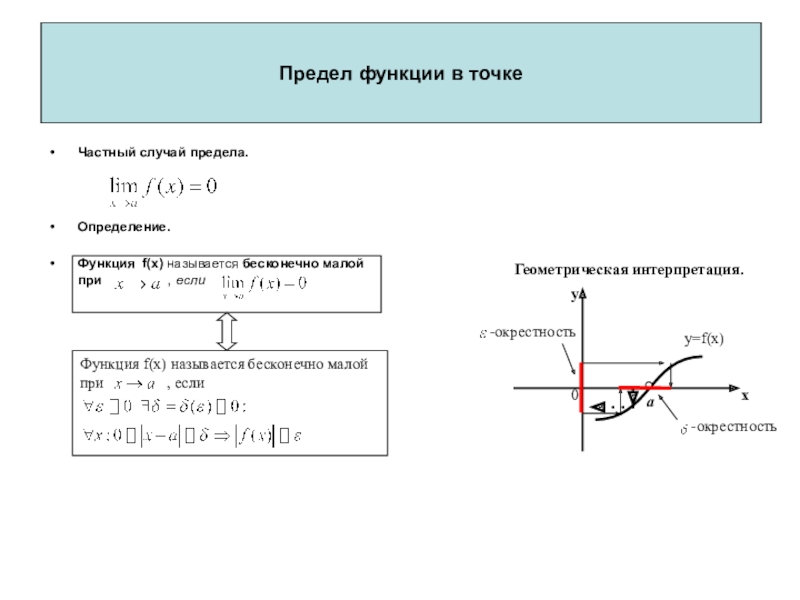
Слайд 42Частный случай предела.
Определение.
Функция f(x) называется бесконечно малой при
, если
Функция f(x) называется бесконечно малой
при , если
Геометрическая интерпретация.
0
х
y
a
-окрестность
-окрестность
Предел функции в точке
y=f(x)
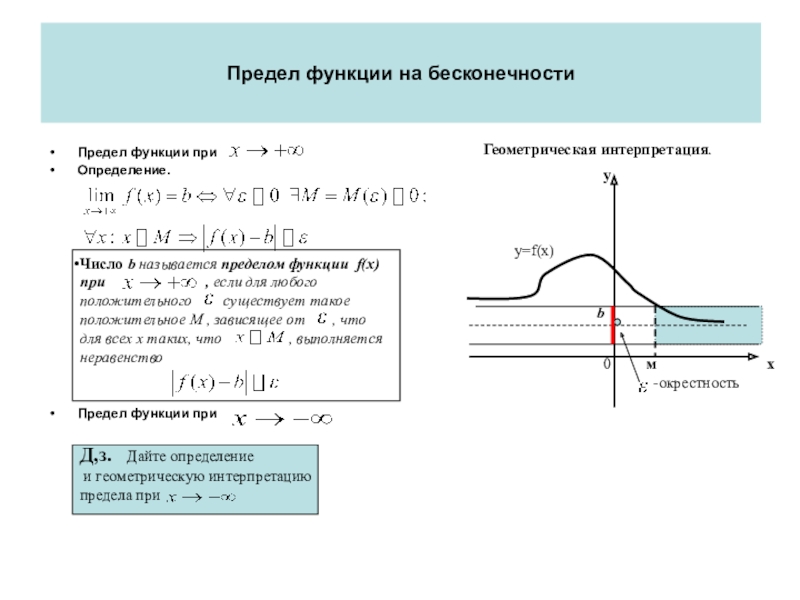
Слайд 43Предел функции на бесконечности
Предел функции при
Определение.
Предел функции при
Число b называется
пределом функции f(x) при
, если для любого положительного существует такое положительное М , зависящее от , что для всех х таких, что , выполняется неравенствоД,з. Дайте определение
и геометрическую интерпретацию
предела при
0
х
y
y=f(x)
м
-окрестность
b
Геометрическая интерпретация.
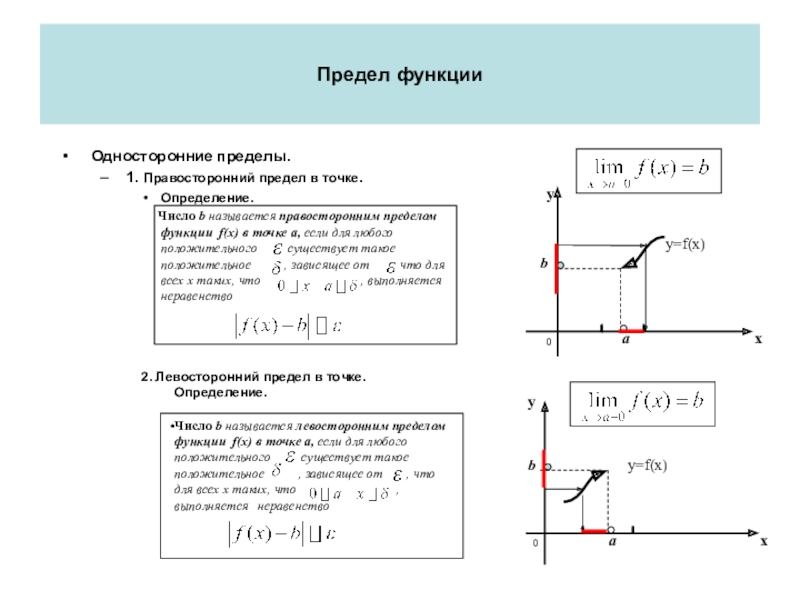
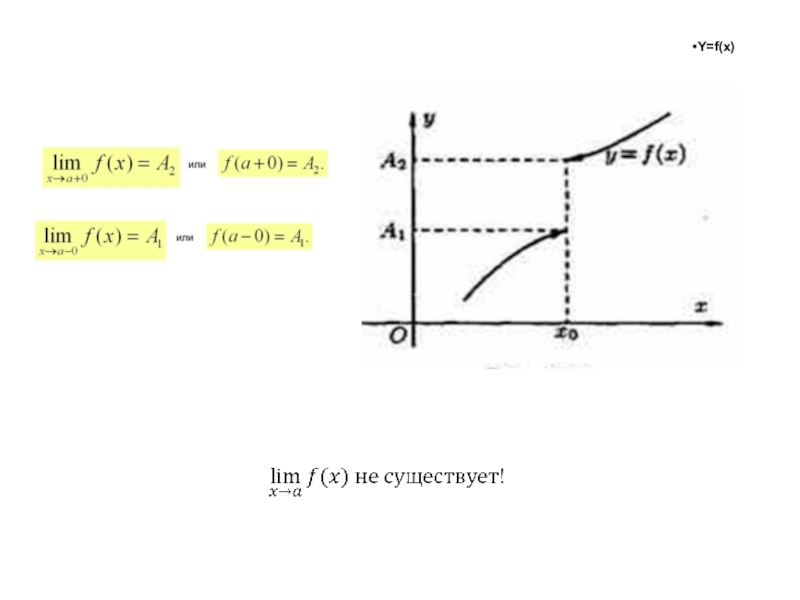
Слайд 45Предел функции
Односторонние пределы.
1. Правосторонний предел в точке.
Определение.
Число
b называется правосторонним пределом функции f(x) в точке a,
если для любого положительного существует такое положительное , зависящее от , что для всех х таких, что , выполняется неравенство2. Левосторонний предел в точке.
Определение.
Число b называется левосторонним пределом функции f(x) в точке a, если для любого положительного существует такое положительное , зависящее от , что для всех х таких, что , выполняется неравенство
0
х
y
a
b
y=f(x)
0
y
х
b
a
y=f(x)
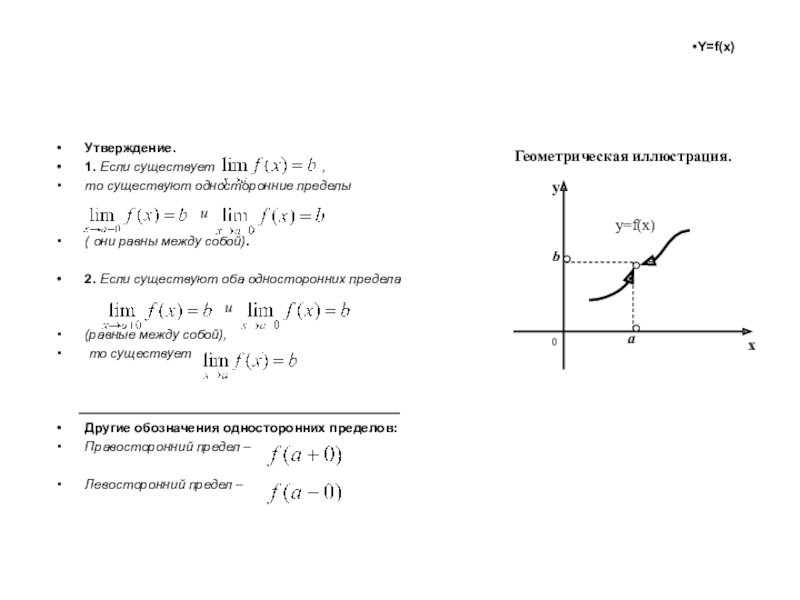
Слайд 46Утверждение.
1. Если существует
,
то существуют односторонние
пределы( они равны между собой).
2. Если существуют оба односторонних предела
(равные между собой),
то существует
Другие обозначения односторонних пределов:
Правосторонний предел –
Левосторонний предел –
и
и
Геометрическая иллюстрация.
0
х
y
a
b
y=f(x)
