Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Содержание
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
- 2. Ротатабельные Планы второго порядкаРотатабельным называют планирование, для
- 3. Ротатабельные Планы второго порядкаБокс и Хантер предложили
- 4. Ротатабельные Планы второго порядка
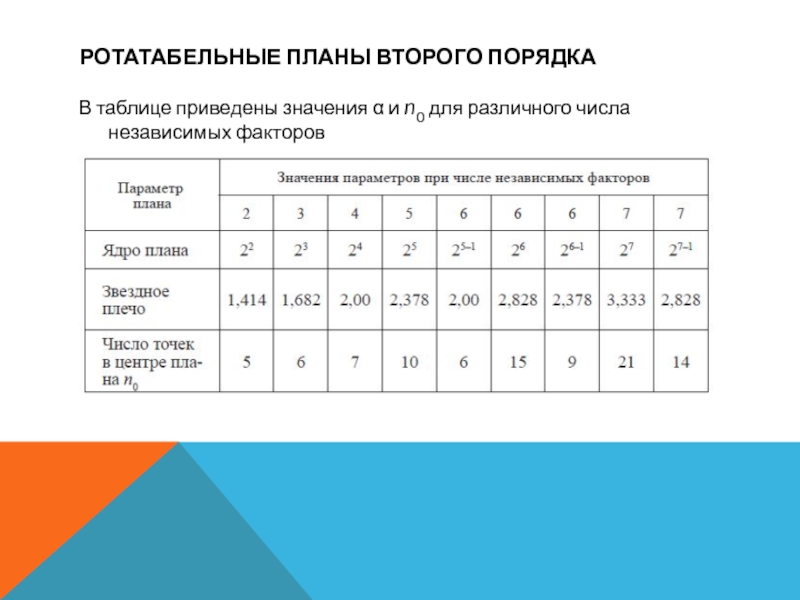
- 5. Ротатабельные Планы второго порядкаВ таблице приведены значения и n0 для различного числа независимых факторов
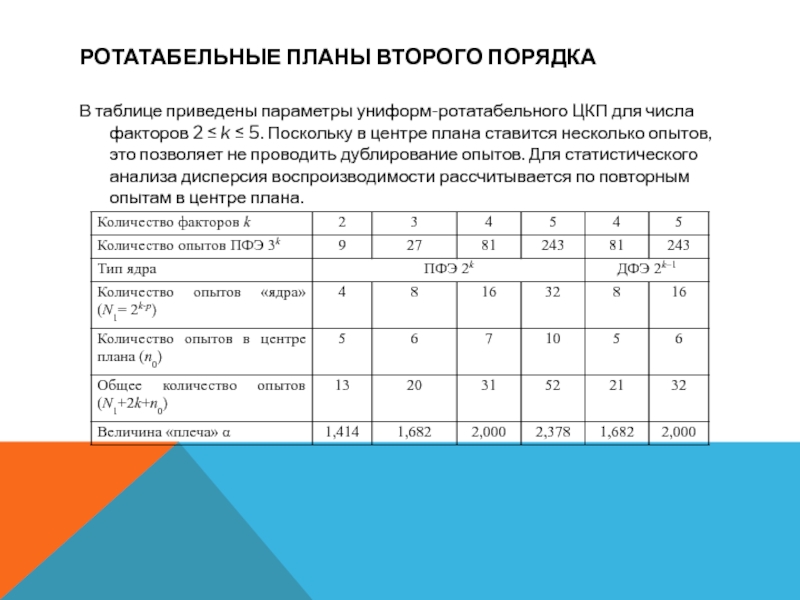
- 6. Ротатабельные Планы второго порядкаВ таблице приведены параметры
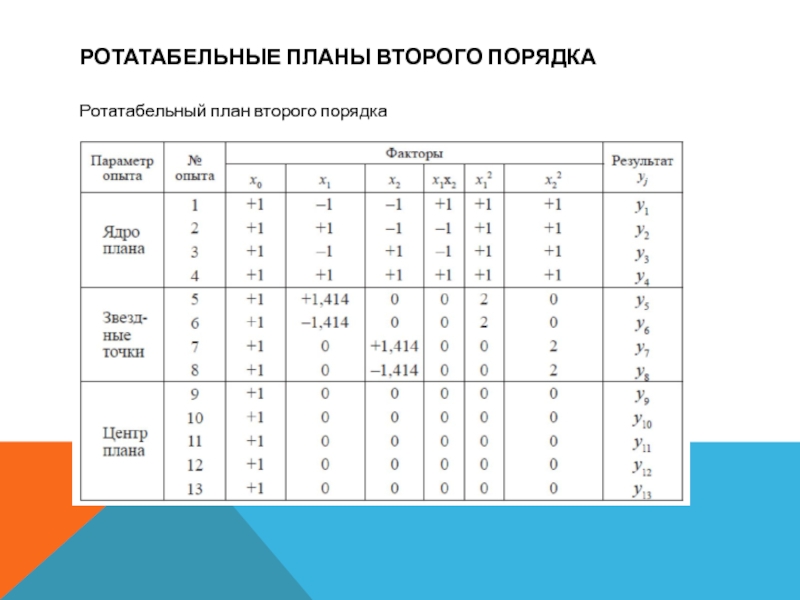
- 7. Ротатабельные Планы второго порядкаРотатабельный план второго порядка
- 8. Ротатабельные Планы второго порядка
- 9. Ротатабельные Планы второго порядка
- 10. Ротатабельные Планы второго порядка
- 11. Ротатабельные Планы второго порядкаМатрица ротатабельного планирования неортогональна,
- 12. Ротатабельные Планы второго порядкаПо опытам в центре
- 13. Ротатабельные Планы второго порядкаПроверяют адекватность по F-критериюУравнение адекватно, если F
- 14. Используемая литература1. Математическое моделирование металлургических процессов в
- 15. Скачать презентанцию
Ротатабельные Планы второго порядкаРотатабельным называют планирование, для которого дисперсия отклика (выходного параметра) y, предсказанного уравнением регрессии, постоянна для всех точек, находящихся на равном расстоянии от центра эксперимента. Экспериментатору заранее не известно,
Слайды и текст этой презентации
Слайд 2Ротатабельные Планы второго порядка
Ротатабельным называют планирование, для которого дисперсия отклика
Слайд 3Ротатабельные Планы второго порядка
Бокс и Хантер предложили ротатабельные планы второго
порядка. Для того чтобы композиционный план был ротатабельным, величину звездного
плеча выбирают из условияили в общем случае
где k – число факторов; р – дробность реплики (для ПФЭ р = 0, для полуреплики р = 1, для четвертьреплики р = 2 и т.д.). Число точек в центре плана n0 увеличивают.
Слайд 5Ротатабельные Планы второго порядка
В таблице приведены значения и n0
для различного числа независимых факторов
Слайд 6Ротатабельные Планы второго порядка
В таблице приведены параметры униформ-ротатабельного ЦКП для
числа факторов 2 ≤ k ≤ 5. Поскольку в центре
плана ставится несколько опытов, это позволяет не проводить дублирование опытов. Для статистического анализа дисперсия воспроизводимости рассчитывается по повторным опытам в центре плана.Слайд 11Ротатабельные Планы второго порядка
Матрица ротатабельного планирования неортогональна, следовательно, если какой-либо
из квадратичных эффектов оказался незначимым, то после его исключения коэффициенты
уравнения регрессии необходимо пересчитать заново.При использовании ротатабельных планов второго порядка дисперсию воспроизводимости можно определить по опытам в центре плана.
При проверке адекватности уравнения регрессии, полученного по ротатабельному плану второго порядка, поступают следующим образом.
Находят остаточную сумму квадратов
с числом степеней свободы
Слайд 12Ротатабельные Планы второго порядка
По опытам в центре плана определяют сумму
квадратов воспроизводимости
с числом степеней свободы m2= n0–1.
Далее находят сумму квадратов,
характеризующих неадекватность число степеней свободы которой равно