Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое моделирование
Содержание
- 1. Математическое моделирование
- 2. Основные положенияНаука — сфера человеческой деятельности, направленной
- 3. Основные положенияКак получить достоверные знания?- пассивно-созерцательная теория
- 4. Основные положенияНастоящая революция в методологии научных исследований
- 5. ЭкспериментЭксперимент может проводиться с целью:— определить, какие
- 6. ЭкспериментТеория эксперимента — наука, занимающаяся вопросами правильной
- 7. Эксперимент Исследование машины или процесса начинается с разработки
- 8. ЭкспериментМатематическая модель процесса представляет собой аналитическое описание
- 9. Эксперимент
- 10. Эксперимент
- 11. Эксперимент
- 12. Практическое занятие №1ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОЙ ОТНОСИТЕЛЬНОЙ ОШИБКИ ФУНКЦИИДля
- 13. Практическое занятие №1 маятник №1Примем длину нити
- 14. Практическое занятие №1 маятник №1Таблица 1 Результаты 50 измерений
- 15. Практическое занятие №1 маятник №2Уменьшите длину маятника
- 16. Практическое занятие №1 маятник №3Уменьшите длину маятника
- 17. Практическое занятие №1 маятник №4Уменьшите длину маятника
- 18. Погрешности результатов измерений
- 19. Погрешности результатов измерений
- 20. Погрешности результатов измерений Систематической называется погрешность, которая при
- 21. Погрешности результатов измеренийСлучайной называется погрешность, обусловленная действием
- 22. Погрешности результатов измерений Рис. Пример данных, иллюстрирующий различие
- 23. Погрешности результатов измеренийинструментальные (приборные или аппаратурные) погрешности
- 24. Погрешности результатов измеренийметодические погрешности – это погрешности,
- 25. Погрешности результатов измеренийсубъективные погрешности, обусловленные особенностями исследователя.Следует
- 26. Законы распределения вероятностей случайных величинСлучайные величины бывают
- 27. Законы распределения вероятностей случайных величинИсследователь при постановке
- 28. Законы распределения вероятностей случайных величинДля дискретных случайных
- 29. Законы распределения вероятностей случайных величин2. В графической
- 30. Полигон и гистограмма
- 31. Практическое занятие №1Построить полигон распределения времени колебаний
- 32. Практическое занятие №1Таблица Построение полигона распределения времени
- 33. Практическое занятие №1Построить точечную ломаную диаграмму - полигон
- 34. Список литературыБойко Н. Г. Основы научных исследований.
- 35. Скачать презентанцию
Основные положенияНаука — сфера человеческой деятельности, направленной на выработку и систематизацию достоверных знаний о действительности [1].Цель научного исследования — выявление новых закономерностей того или иного процесса (получение неизвестных до этого зависимостей
Слайды и текст этой презентации
Слайд 2Основные положения
Наука — сфера человеческой деятельности, направленной на выработку и
систематизацию достоверных знаний о действительности [1].
новых закономерностей того или иного процесса (получение неизвестных до этого зависимостей между величинами, характеризующие исследуемый процесс), в конечном итоге - получение новых знаний о действительности.Слайд 3Основные положения
Как получить достоверные знания?
- пассивно-созерцательная теория Дидро [2] (главное
это ощущения);
идеализм Гегеля (истина существует сама
по себе - высший разум,
космос);агностицизм Д. Юма и И. Канта (замена знания верой );
скептицизм (наши чувства нас обманывают и доверять им нельзя. Рассказывают шутливую историю о Пирроне. Когда он умер, на его могиле, якобы, его оппоненты поставили эпитафию: «Умер ли ты, Пиррон? -"Не знаю!"»
Известная фраза Рене Декарта - Cogito, ergo sum (я мыслю, значит я существую)
Слайд 4Основные положения
Настоящая революция в методологии научных исследований произошла лишь тогда,
когда роль критерия истинности знания безоговорочно была отдана практике.
Можно выделить
три основных этапа познания:— сбор эмпирической информации об объекте исследования;
— систематизация и анализ информации, разработка теории;
— проверка теории на практике.
Достоверными могут считаться лишь знания, которые подтверждаются практикой.
Слайд 5Эксперимент
Эксперимент может проводиться с целью:
— определить, какие величины и насколько
влияют на исследуемый объект (процесс) — такой эксперимент называется отсеивающим;
—
установить зависимости между входными и выходнымивеличинами, характеризующими исследуемый объект (процесс) —
такие зависимости называются эмпирическими;
— проверить (подтвердить или опровергнуть) результаты теоретических исследований — установить адекватность (соответствие) теоретических положений и моделей действительности;
— выполнить оптимизацию исследуемого объекта (процесса),
т.е. найти такие значения параметров, при которых объект функционирует наилучшим образом.
Слайд 6Эксперимент
Теория эксперимента — наука, занимающаяся вопросами правильной организации экспериментальных исследований
— включает три основных направления:
1. Моделирование и подобие — определяет,
как должен проводиться эксперимент, какие величины, характеризующие исследуемый объект или процесс, должны измеряться при экспериментальных исследованиях, и как обрабатывать результаты исследований, чтобы полученные закономерности были справедливы как для данного объекта (процесса), так и для группы ему подобных.2. Планирование эксперимента — совокупность методов и процедур, применение которых при организации и проведении эксперимента позволяет получить искомые зависимости с минимальными временными и материальными затратами.
3. Статистическая обработка экспериментальных данных — совокупность методик, позволяющих получить достоверные результаты на основе данных, содержащих погрешности.
Слайд 7Эксперимент
Исследование машины или процесса начинается с разработки физической модели, а
затем, на ее основании, строится математическая модель.
Производится решение математической
модели и анализ полученных результатов. Проверяется адекватность, т.е. соответствие этой модели действительной картине процесса.
Физическая модель процесса или системы представляет собой ее абстрагированное символическое описание.
Для примера рассмотрим на рис. 1 МАТЕМАТИЧЕСКИЙ МАЯТНИК (тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела).
Слайд 8Эксперимент
Математическая модель процесса представляет собой аналитическое описание связей между отдельными
элементами физической модели.
В положении равновесия, когда маятник висит по отвесу,
сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести Fτ = –mg sin φ (рис. 1). Рисунок 1.
Математический маятник. φ – угловое отклонение маятника от положения равновесия, x = lφ – смещение маятника по дуге
Слайд 12Практическое занятие №1
ОПРЕДЕЛЕНИЕ ПРЕДЕЛЬНОЙ ОТНОСИТЕЛЬНОЙ ОШИБКИ ФУНКЦИИ
Для выполнения работы используются:
1.
Измерительная линейка с пределом измерений до 1000 мм, с допустимой инструментальной
погрешностью 0,2 мм.2. Электронный секундомер с ценой деления 0,01 с. Инструментальная погрешность секундомера мала и ее можно не учитывать при измерениях.
Слайд 13Практическое занятие №1
маятник №1
Примем длину нити маятника около 500 мм.
Отклонив маятник на угол 15-20 градусов от положения равновесия, отпустим
его и, по прошествии нескольких колебаний, в момент прохождения маятником крайнего положения включим секундомер. Остановим его при прохождении того же крайнего положения. Указанные измерения провести n = 50 раз, данные занести в таблицу 1. Вычисления производить в электронной таблице Microsoft Office Excel.t1
t2
T=t1+t2
Слайд 15Практическое занятие №1
маятник №2
Уменьшите длину маятника до 450 мм. Провести
измерения один раз.
Таблица 2 Результаты 1 измерения
Слайд 16Практическое занятие №1
маятник №3
Уменьшите длину маятника до 400 мм. Провести
измерения пять раз.
Таблица 3 Результаты 5 измерений
Слайд 17Практическое занятие №1
маятник №4
Уменьшите длину маятника до 350 мм. Провести
измерения пятнадцать раз.
Таблица 4 Результаты 15 измерений
Слайд 20Погрешности результатов измерений
Систематической называется погрешность, которая при повторных экспериментах остается
постоянной или изменяется закономерно. Наличие систематических погрешностей может быть обнаружено
путем анализа условий измерения одного и того же значения измеряемой величины разными методами или приборами. Систематические погрешности нельзя уменьшить увеличением числа параллельных опытов. Должны устраняться вызывающие их причины. Общим методом выявления причин систематических погрешностей является калибровка (поверка), которая представляет собой поверку прибора во всем диапазоне измеряемой величины с помощью известного эталона.Слайд 21Погрешности результатов измерений
Случайной называется погрешность, обусловленная действием ряда причин, меняющихся
случайным образом от эксперимента к эксперименту. Значение этой погрешности не
может быть определено в каждом эксперименте и на нее невозможно оказать влияние. К случайным относятся непостоянные погрешности, причины возникновения которых неизвестны. Таким образом, случайные погрешности представляют собой беспорядочные флуктуации показаний прибора относительно истинного значения измеряемой величины. Для исследования случайных погрешностей, возникающих при проведении эксперимента, широко используются математическая статистика и теория вероятностей.Слайд 22Погрешности результатов измерений
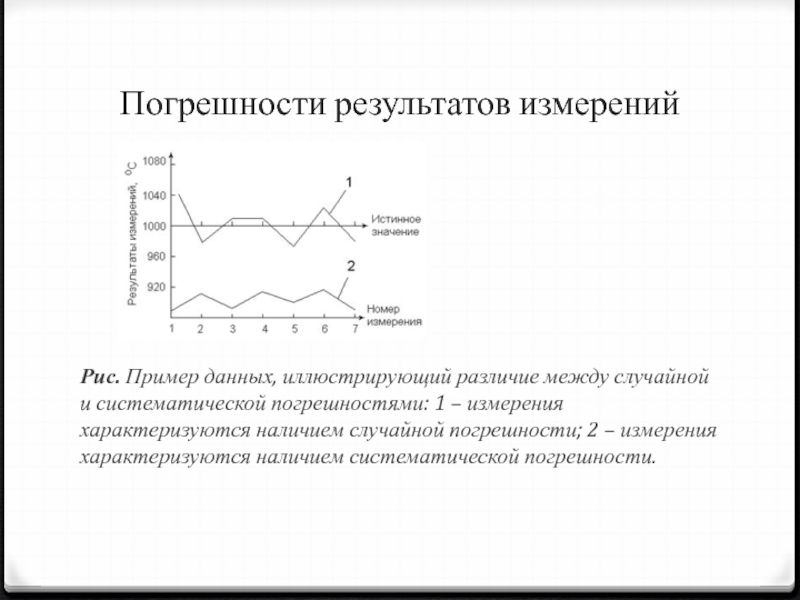
Рис. Пример данных, иллюстрирующий различие между случайной и
систематической погрешностями: 1 – измерения характеризуются наличием случайной погрешности; 2
– измерения характеризуются наличием систематической погрешности.Слайд 23Погрешности результатов измерений
инструментальные (приборные или аппаратурные) погрешности средств измерений называются
такие, которые принадлежат данному средству измерений, они могут быть определены
при его испытаниях и занесены в его паспорт. Принято различать основную погрешность средств измерений, т.е. погрешность в условиях, принятых за нормальные, и дополнительную погрешность, вызванную отклонением влияющих параметров за пределы области нормальных значений (вибрации, влажности среды, инерцией и т.п.);Слайд 24Погрешности результатов измерений
методические погрешности – это погрешности, которые не могут
быть приписаны данному прибору, не смогут быть указаны в его
паспорте, т.е. связаны не с самим прибором, а с методикой проведения измерений. Очень часто причиной возникновения методической погрешности является то, что организуя измерения, измеряют или вынуждены измерять не ту величину, которую в принципе требуется измерять, а некоторую другую, близкую, но не равную ей.Отличительной особенностью методических погрешностей является то, что они могут быть определены лишь путем создания математической модели исследуемого объекта и не смогут быть найдены сколь угодно тщательным исследованием лишь самого измерительного прибора.
Слайд 25Погрешности результатов измерений
субъективные погрешности, обусловленные особенностями исследователя.
Следует иметь ввиду, что
полностью исключить систематические погрешности невозможно, так как методы и средства,
с помощью которых обнаруживаются и оцениваются систематические погрешности, сами имеют свои погрешности.Грубые погрешности (промахи) возникают вследствие непредвиденного изменения условий эксперимента, качества измерений, поломок прибора, неправильной записи в рабочих журналах, механических ударах прибора, неправильном отчете показаний прибора, отключении источника питания и т.п. Результат, содержащий грубую ошибку, резко отличается по величине от остальных измерений. Такие результаты должны быть исключены из рассмотрения до математической обработки результатов эксперимента.
Слайд 26Законы распределения вероятностей случайных величин
Случайные величины бывают дискретными и непрерывными.
Дискретные
величины способны принимать лишь ограниченное число значений, известных заранее, например
количество успешных опытов или каких-либо объектов, выражаемое целым числом, лежащем в заданном интервале.Непрерывные величины могут принимать любое значение в некотором интервале. В большинстве случаев результаты опытов являются непрерывными случайными величинами.
Предположим, какая-либо случайная величина измеряется бесконечное число раз. Полученное в результате множество, которое
содержит в себе любые значения величины, которые можно получить
при реальном эксперименте, называется гипотетической генеральной совокупностью.
Слайд 27Законы распределения вероятностей случайных величин
Исследователь при постановке опытов делает конечное,
обычно небольшое, количество измерений. Их можно рассматривать как случайную выборку
из гипотетической генеральной совокупности.Задача обработки сводится к определению по данным выборки показателей, оценивающих параметры генеральной совокупности.
Для правильного решения этой задачи необходимо знать закон распределения вероятностей случайной величины — зависимость, связывающую значения случайной величины и вероятность появления этих значений.
Слайд 28Законы распределения вероятностей случайных величин
Для дискретных случайных величин закон распределения
вероятностей
может быть задан:
1. В табличной форме:
где xi – значения случайной
величины X (заглавными литерами принято обозначать сами случайные величины, а прописными — их значения); Pi – вероятность, с которой случайная величина примет соответствующее значение.Слайд 29Законы распределения вероятностей случайных величин
2. В графической форме — в
виде полигона распределения
вероятностей или гистограммы. Отличие заключается в том, что
в полигоне по оси ординат откладывается вероятность Pi, а в гистограмме — плотность распределения вероятностей — отношение вероятности к величине интервала Δx между значениями: pi =Pi /Δx
Тогда вероятность Pi = piΔx есть площадь соответствующего
столбца.
3. В аналитической форме — в виде некоторой функции, отражающей зависимость вероятности от значения случайной величины.
Слайд 31Практическое занятие №1
Построить полигон распределения времени колебаний для маятника № 1.
Для
этого в таблице Excel скопировать столбец с ti и сделать
его сортировку по-возрастанию. Определить границы полигона по наименьшему и наибольшему значению периода колебаний, округляя их до 0,5 с. Сформировать новый столбец с шагом 0,5 с и в соседние столбцы записать середины интервалов и количество попаданий текущего периода колебаний в каждый интервал (пример табл.).Слайд 32Практическое занятие №1
Таблица Построение полигона распределения времени колебаний маятника
В случае,
когда ti совпадает с границами интервалов, распределить их поровну между
ними.Слайд 34Список литературы
Бойко Н. Г. Основы научных исследований. Курс лекций //Н.
Г. Бойко, О. В. Федоров - Донецк : ДонНТУ, 2007.
– 76 с.Философия о познаваемости мира, человека и его бытия. Код доступа: http://poisk-istini.com/literatura/osnovy-filosofii-strjukovskij/filosofiya-o-poznavaemosti-mira-cheloveka-i-ego-bitiya
Открытый колледж. Физика. Код доступа: https://physics.ru/

![Математическое моделирование Основные положенияНаука — сфера человеческой деятельности, направленной на выработку и систематизацию Основные положенияНаука — сфера человеческой деятельности, направленной на выработку и систематизацию достоверных знаний о действительности [1].Цель научного](/img/thumbs/d2e2224c5bea45e6d9a7a47a6cbe7213-800x.jpg)
![Математическое моделирование Основные положенияКак получить достоверные знания?- пассивно-созерцательная теория Дидро [2] (главное это Основные положенияКак получить достоверные знания?- пассивно-созерцательная теория Дидро [2] (главное это ощущения);идеализм Гегеля (истина существует самапо себе](/img/tmb/4/343941/a2a84c576a0b97f0da807e4c84b81e73-800x.jpg)












































![Звуки [ Г ], [ Г ' ]](/img/tmb/7/641721/126d2193ce288c820a428ffd0ebbf728-800x.jpg)


