некотором интервале и равновероятны.
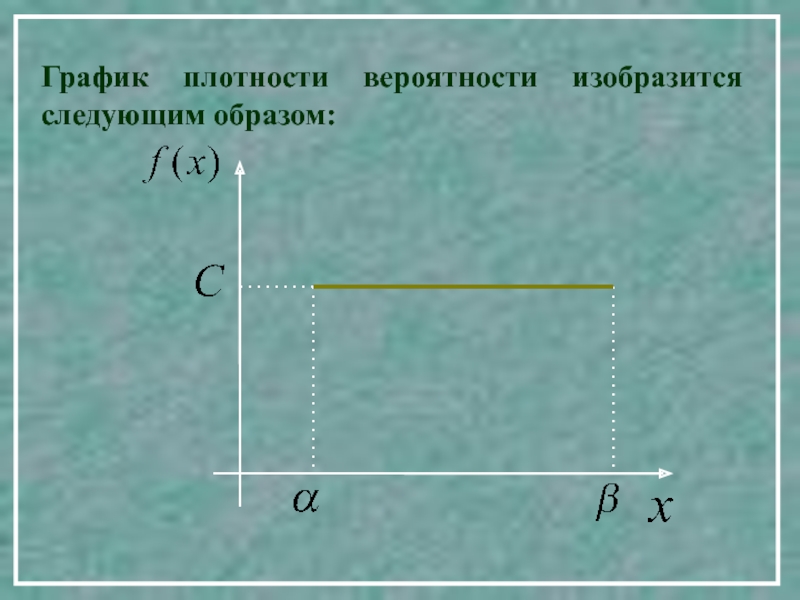
Плотность вероятности такой случайной величины будет иметь
вид:Где с - некоторая постоянная.
20. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ





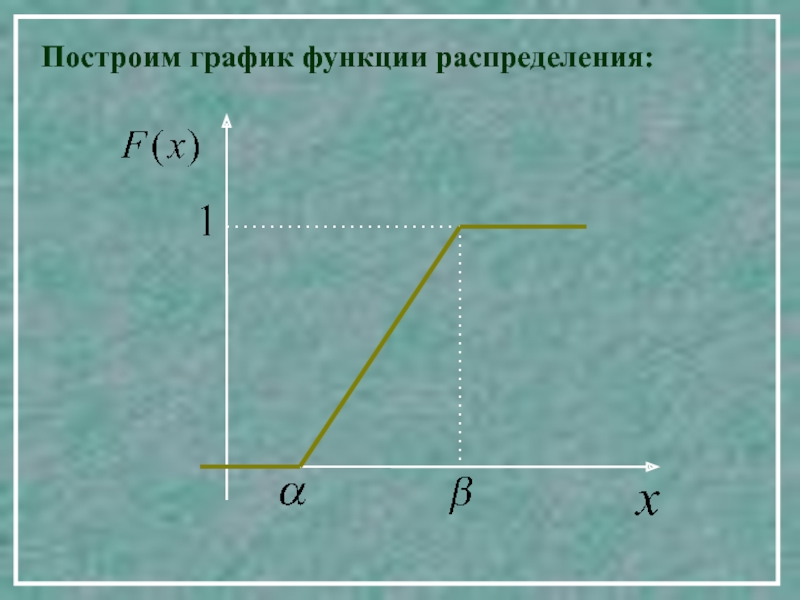


![Рассмотрим непрерывную случайную величину Х, возможные значения которой лежат в Пусть случайная величина Х равномерно распределена на участке [0;100]. Найти вероятности: Р(0 Пусть случайная величина Х равномерно распределена на участке [0;100]. Найти вероятности: Р(0](/img/thumbs/5ffb38222b66704fff579d7052eafd96-800x.jpg)