Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое моделирование Понятие математической модели Методы определения
Содержание
- 1. Математическое моделирование Понятие математической модели Методы определения
- 2. Понятие математической моделиМатематической моделью объекта называют его
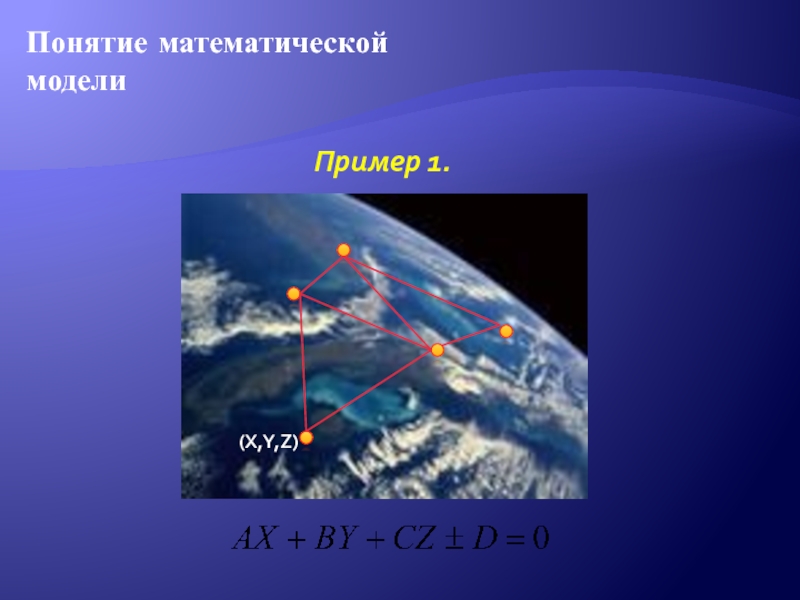
- 3. Понятие математической моделиПример 1.(X,Y,Z)
- 4. Понятие математической моделиПри изучении сложных объектов приходится
- 5. Понятие математической моделиПример 2.Пусть требуется составить математическую
- 6. Методы определения математических моделейВ математических
- 7. Методы определения математических моделейАксиоматический
- 8. Методы определения математических моделейКонструктивный метод
- 9. Представления математических моделейАналитическая формаАлгоритмическая формаЦифровая формаГрафическая форма
- 10. Представления математических моделейАналитическая формаЗапись модели
- 11. Представления математических моделейПример . Пусть
- 12. Представления математических моделейАналитическая формаМатематические модели,
- 13. Представления математических моделейАлгоритмическая формаМодель представляется
- 14. Представления математических моделейЦифровая формаЭто упорядоченный
- 15. Представления математических моделейГрафическая формаГрафическая форма
- 16. Эквивалентная схема по своим свойствам эквивалентна некоторому
- 17. Представления математических моделейДиаграмма (рисунок, фигура) - это один из способов изображения зависимости между объектами.ГрафикГистограмма
- 18. Представления математических моделейЯзык графов широко
- 19. Множество точек графа называют множеством вершин, а
- 20. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Понятие математической модели
Математической моделью объекта называют его описание математическими средствами,
позволяющее выводить суждение о некоторых свойствах объекта при помощи формальных
процедур.Изоморфизм – сходство форм при качественном различии явлений
В наиболее общем виде математическая модель объекта представляется уравнением
F(X, Y)= const
где X, Y - векторы управляемых и неуправляемых параметров модели.
Слайд 4Понятие математической модели
При изучении сложных объектов приходится учитывать большое число
взаимосвязанных факторов, при этом реально доступная информация может иметь любую
степень детерминированности, быть плохо формализуемой, поступать в произвольной форме и эволюционировать во времени. При математическом моделировании факторы отображаются в виде математических конструкций - таких, как параметры состояния объекта и среды, ограничения на область совместного и согласованного изменения этих параметров и т.д.Формализация предполагает построение некоторой структуры с целью логического описания и понимания формализуемого объекта
Слайд 5Понятие математической модели
Пример 2.
Пусть требуется составить
математическую модель направления АВ.
Решение:
Предположим,
что направление наблюдается в теодолит и его положение в пространстве
может быть определено зенитным расстоянием Z, горизонтальным направлением А.Тогда математическая модель направления определяется орт вектором в системе координат, у которой:
· ось ОХ имеет направление в "точку нуля" на горизонтальном
круге,
· ось OY перпендикулярна оси ОХ и направлена вправо,
· ось OZ совпадает с осью вращения инструмента и направлена в зенит.
Слайд 6 Методы определения математических моделей
В математических моделях осуществляется упрощенное,
приближённое и абстрактное описание объектов моделирования. Это происходит в результате
замены моделируемых объектов, математическими объектами (числами, векторами, множествами, функциями и т.д.)Два метода определения математических моделей: Аксиоматический Конструктивный
Слайд 7 Методы определения математических моделей
Аксиоматический метод
При использовании аксиоматического
метода осуществляется переход из предметной области к абстрактной модели с
объектами произвольной природы, отношениями и операциями, которая определяется непротиворечивым набором правил (аксиом).Непротиворечивость системы аксиом (совместимость) - это свойство, состоящее в том, что из такой системы аксиом нельзя вывести противоречия, т. е. двух предложений, одно из которых является отрицанием другого.
Основной недостаток аксиоматического метода состоит в том, что он лишь формирует утверждение о существовании модели и не определяет пути реализации.
Слайд 8 Методы определения математических моделей
Конструктивный метод связывает утверждение о
существовании модели с возможностью её построения. В связи с этим
конструктивное определение модели неоднозначно и зависит от способа построения модели. Построение конструктивной модели, удовлетворяющей некоторой системе аксиом, доказывает непротиворечивость аксиоматического определения.При конструктивном определении модели очень часто пользуются уже известными моделями. Например, алгебра матриц, аналитическая геометрия и т. д.
Слайд 9 Представления математических моделей
Аналитическая форма
Алгоритмическая форма
Цифровая форма
Графическая форма
Слайд 10 Представления математических моделей
Аналитическая форма
Запись модели выполняется в виде
явных, неявных, параметрических функций, интегральных и дифференциальных уравнений или других
аналитических выражений, связывающих управляемые и неуправляемые переменные и цель моделирования.Математические модели, представленные в аналитической форме, можно преобразовывать в соответствии с правилами и законами математики, получать решение и делать выводы, основанные на аналитических преобразованиях.
Слайд 11 Представления математических моделей
Пример .
Пусть заданы два направления АВ
и CD,
для которых получены математические
модели:
направление АВ => r1
(x1,y1,z1) направление АС => r2 (x2,y2,z2) Требуется составить математическую модель для определения угла между этими направлениями. Решение: Воспользуемся формулой для определения скалярного произведения двух векторов
где φ - угол между векторами r1 и r2
из которого найдём:
Слайд 12 Представления математических моделей
Аналитическая форма
Математические модели, представленные в аналитической
форме, позволяют выявить наиболее общие закономерности, присущие объекту моделирования.
Достоинством
математических моделей в аналитической форме служит высокая степень общности и значимости результатов моделирования. Недостатком - высокая чувствительность к степени сложности объекта моделирования, так как сложные объекты аналитически представляются грубо и неточно.
.
Среди моделей представленных в аналитической форме выделяют модели в инвариантной форме.
Инвариантность модели определяется относительно какой-либо совокупности преобразований
Слайд 13 Представления математических моделей
Алгоритмическая форма
Модель представляется в форме алгоритма,
т.е. в виде точного предписания последовательности некоторой системы операций над
исходными данными с целью получения результата.Для определения модели в алгоритмической форме необходимо указать:
1. множество исходных данных,
2. множество возможных
результатов,
3. множество промежуточных
результатов (может
отсутствовать),
4. критерий начала выполнения
алгоритма,
5. критерий окончания
выполнения алгоритма,
6. правила выполнения
алгоритма,
7. правила извлечения
результата
Слайд 14 Представления математических моделей
Цифровая форма
Это упорядоченный набор чисел и
алгоритм, который данному набору чисел ставит в соответствие функцию F,
представляющую исходный объект в соответствии с критериями качества моделирования.Примером цифровой модели служит цифровая модель рельефа, состоящая из последовательности отметок точек, отделённых друг от друга конечными интервалами, и алгоритмов аппроксимации этой информации.
Слайд 15 Представления математических моделей
Графическая форма
Графическая форма модели - это
её представление на некотором графическом языке, например, на языке эквивалентных
схем, диаграмм, языке графов и т. д.Слайд 16Эквивалентная схема по своим свойствам эквивалентна некоторому реальному устройству и
наглядно отражает сущность процессов в нём.
Примером может служить блок -
схема программы или блок - схема конструкции какого-либо объекта. Она представляет графическое изображение набора операционных элементов модели, характеризующихся определённой математической зависимостью между переменными на выходе и входе. Поэтому математическое описание эквивалентной схемы тождественно математическому описанию моделируемого объекта. Представления математических моделей
Слайд 17 Представления математических моделей
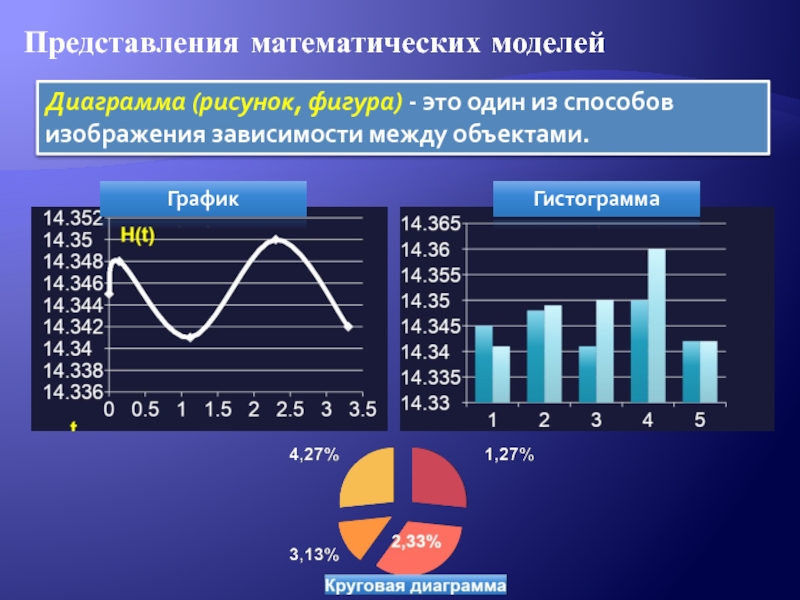
Диаграмма (рисунок, фигура) - это один
из способов изображения зависимости между объектами.
График
Гистограмма
Слайд 18 Представления математических моделей
Язык графов широко используется при создании
и описании различных математических моделей систем в экономике, биологии и
т. д.Объект моделирования рассматривается как множество элементарных объектов, между которыми имеются некоторые зависимости. Элементарные объекты интерпретируются как точки, а связи (зависимости) между ними - как линии. Объект, состоящий из двух множеств (множества точек и множества линий), которые между собой находятся в некотором отношении, называют графом.
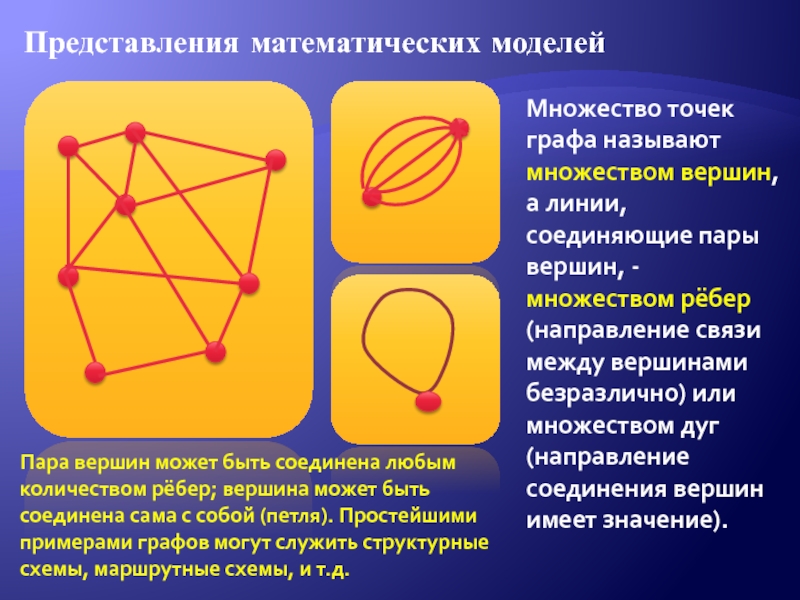
Слайд 19Множество точек графа называют множеством вершин, а линии, соединяющие пары
вершин, - множеством рёбер (направление связи между вершинами безразлично) или
множеством дуг (направление соединения вершин имеет значение). Представления математических моделей
Пара вершин может быть соединена любым количеством рёбер; вершина может быть соединена сама с собой (петля). Простейшими примерами графов могут служить структурные схемы, маршрутные схемы, и т.д.