Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика
Содержание
- 1. Математика
- 2. Содержание РАЗДЕЛ 1. Элементы линейной (задача 3)РАЗДЕЛ 2. Элементы математического анализа (задачи 4-5)
- 3. Раздел 1. Элементы линейной алгебры§ 1. Матрицы.
- 4. ОПРЕДЕЛЕНИЕ. Матрицей называется прямоугольная таблица из m
- 5. Пример
- 6. ВИДЫ МАТРИЦ
- 7. 4) Квадратная матрица называется единичной, если ее
- 8. 6) Квадратная матрица называется диагональной, если элементы,
- 9. Действия над матрицамиРавенство матрицСложение (вычитание) матрицСумма и
- 10. Умножение матрицы на числоНайти значение выражения:При умножении
- 11. Умножение матрицПроизведение матриц A * B определено
- 12. Слайд 12
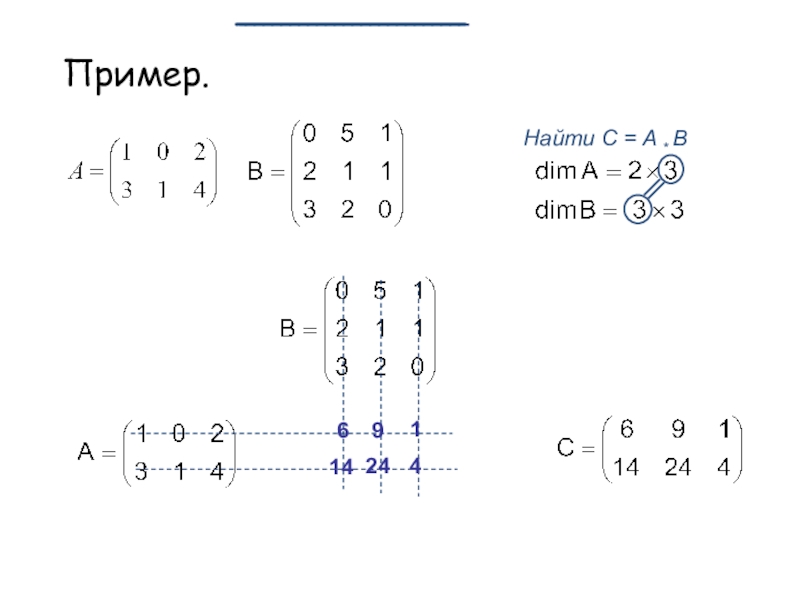
- 13. Пример.Найти С = A * B69114244
- 14. Пример Найти произведение матриц АВ и проверить, перестановочны ли матрицы Решение:
- 15. 2) Определитель 2 - го порядка.§ 2.
- 16. a11a22a33+a12a23a31+ a13a21a32-- ( a13a22a31+ a21a12a33+ a32a23a11 «+»«-»3) Определитель 3 - го порядка. Правило треугольников. )
- 17. Метод треугольника применим только для определителей 3 порядкаПример.
- 18. Свойства определителя произвольного порядка:1. Определитель
- 19. 7. Значение определителя не изменится, если к
- 20. §3. Обратная матрицаТеорема. Обратная матрица существует и
- 21. Где - алгебраическое
- 22. Найти обратную матрицу к матрице А
- 23. В результате, обратная матрица имеет вид:
- 24. §4.1. Метод обратной матрицы решения систем линейных
- 25. Тогда систему можно записать так:Найдем решение системы в матричном виде:
- 26. Метод обратной матрицы решения систем линейных уравненийРешить систему методом обратной матрицы.-0,52-5
- 27. §4.2. Метод Крамера.Рассмотрим систему из трех уравнений
- 28. Теорема (правило Крамера).Тогда, если
- 29. Пример: Решить систему уравнений по формулам Крамера. значит система имеет единственное решение, определяемое формулами Крамера
- 30. Рассмотрим систему линейных уравненийгде числа а11, а12,…а33
- 31. Метод Гаусса решения систем линейных уравненийСледующие действия
- 32. Пример: Решить систему уравнений методом Гаусса. Расширенная
- 33. Матрица приведена к треугольному виду, ей соответствует
- 34. Скачать презентанцию
Содержание РАЗДЕЛ 1. Элементы линейной (задача 3)РАЗДЕЛ 2. Элементы математического анализа (задачи 4-5)
Слайды и текст этой презентации
Слайд 1Математика
Контрольная работа (домашняя) по методичке 15876 (с.27), задачи 3,4,5(а,б,в)
Практикумы
«Алгебра» и «Матем.анализ»
Слайд 2Содержание
РАЗДЕЛ 1. Элементы линейной (задача 3)
РАЗДЕЛ 2. Элементы математического
анализа (задачи 4-5)
Слайд 3Раздел 1. Элементы линейной алгебры
§ 1. Матрицы. Операции над ними.
§
2. Определители.
§3. Обратная матрица
§ 4. Решение СЛАУ.
Слайд 4ОПРЕДЕЛЕНИЕ. Матрицей называется прямоугольная таблица из m строк и n
столбцов, содержащая числа или иные математические выражения.
Матрицы обозначаются заглавными буквами
латинского алфавита, элементы матрицы – теми же маленькими буквами.Размерность матрицы обозначается:
количество строк
количество столбцов
Главная диагональ
Побочная диагональ
§ 1. Матрицы. Операции над ними.
Слайд 74) Квадратная матрица называется единичной, если ее элементы, расположенные на
главной диагонали, равны единице, остальные – нулю (обозначается буквой Е):
5) Если все элементы матрицы равны нулю, то она называется нулевой матрицей и обозначается символом 0.
Слайд 86) Квадратная матрица называется диагональной, если элементы, стоящие вне главной
диагонали равны нулю
7) Квадратная матрица называется треугольной, если элементы, стоящие
ниже (выше) главной диагонали равны нулю:
Слайд 9Действия над матрицами
Равенство матриц
Сложение (вычитание) матриц
Сумма и разность матриц существуют
только для матриц одинакового размера, при этом соответствующие элементы матриц
складываются или вычитаются.Матрицы равны, если они имеют одинаковую размерность и их соответствующие элементы равны.
Транспонирование матрицы
Операция получения из данной матрицы транспонированной заменой каждой строки столбцом с тем же номером
Слайд 10Умножение матрицы на число
Найти значение выражения:
При умножении матрицы A на
число k получается матрица того же размера, при этом каждый
элемент матрицы A умножается на k.Решение:
Слайд 11Умножение матриц
Произведение матриц A * B определено только тогда, когда
число столбцов матрицы А равно числу строк матрицы В, в
противном случае произведение не существует.Пример 1.
Пример 2.
Слайд 152) Определитель 2 - го порядка.
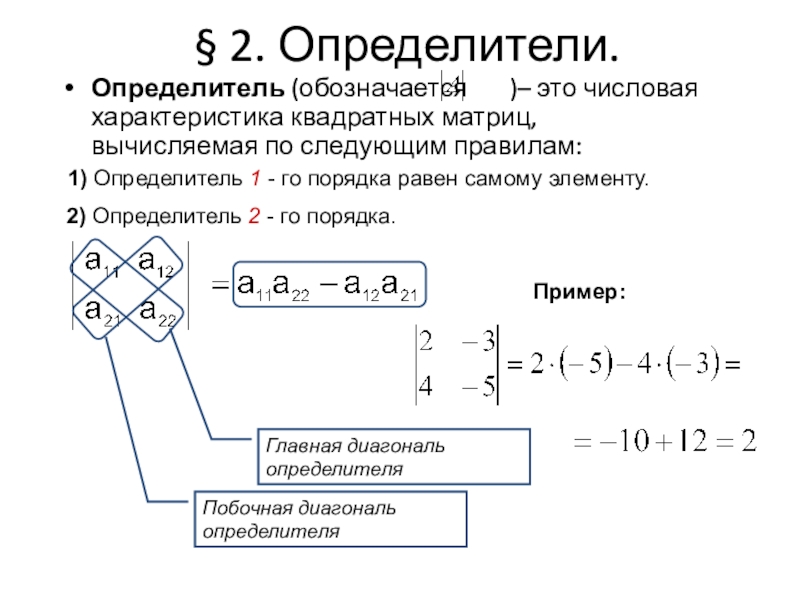
§ 2. Определители.
Определитель (обозначается
)– это числовая характеристика квадратных матриц, вычисляемая по
следующим правилам:1) Определитель 1 - го порядка равен самому элементу.
Пример:
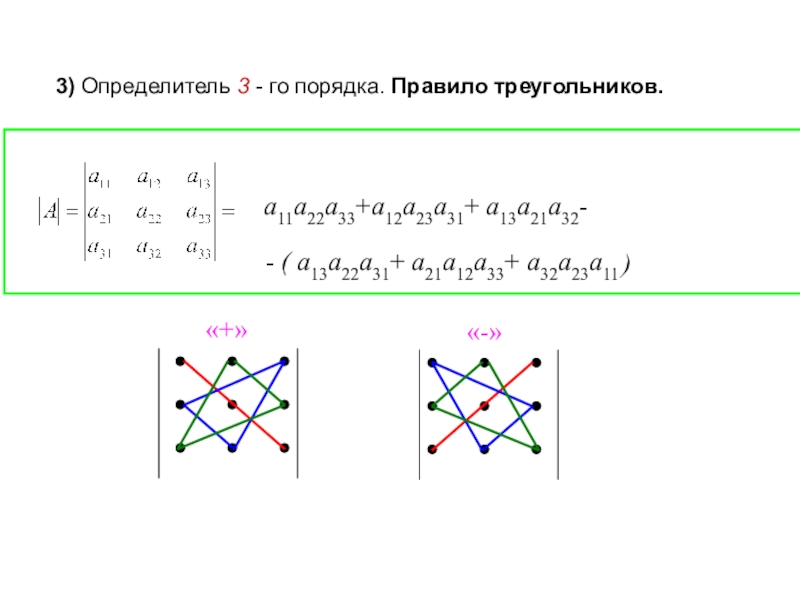
Слайд 16a11a22a33+a12a23a31+ a13a21a32-
- ( a13a22a31+ a21a12a33+ a32a23a11
«+»
«-»
3) Определитель 3 -
го порядка. Правило треугольников.
)
Слайд 18 Свойства определителя произвольного порядка:
1. Определитель матрицы А равен
определителю транспонированной матрицы, т.е.
2. Если все элементы некоторой
строки матрицы А равны 0, то определитель равен 0.3. Общий множитель всех элементов строки определителя можно вынести за знак этого определителя.
4. Если в определителе поменять местами две строки, то он изменит знак на противоположный.
5. Если определитель имеет две равные строки, то он равен 0.
Слайд 197. Значение определителя не изменится, если к элементам его некоторой
строки прибавить соответствующие элементы другой строки, умноженные на одно и
то же число k.6. Если элементы двух строк определителя пропорциональны, то определитель равен 0.
Слайд 20§3. Обратная матрица
Теорема. Обратная матрица существует и единственна тогда и
только тогда, когда .
Определение.
Квадратная матрица А-1 называется обратной матрицей по отношению к квадратной матрице A n - ного порядка, если выполняется условие:АА-1=А-1А=Е,
где A, А-1, Е – одного порядка.
Слайд 21Где - алгебраическое дополнение элемента ai
j
вычисляется по формуле
Mi j - минор элемента ai
j - это oпределитель, который получается из определителя n - го порядка путем вычеркивания i - й строки и j - го столбца, т.е. строки и столбца, на пересечении которых стоит элемент ai j
Слайд 24§4.1. Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы
рассмотрим на примере решения квадратной системы 3 порядка.
Запишем эту
систему в матричном виде. Обозначим:Основная матрица системы
Матрица - столбец неизвестных
Матрица - столбец свободных членов
Слайд 26Метод обратной матрицы решения систем линейных уравнений
Решить систему методом обратной
матрицы.
-0,5
2
-5
Слайд 27§4.2. Метод Крамера.
Рассмотрим систему из трех уравнений с тремя неизвестными:
Δ-
главный определитель системы. Рассмотрим вспомогательные определители, которые получаются из главного
определителя, заменой соответствующего столбца столбцом свободных членов:
Слайд 28Теорема (правило Крамера).
Тогда, если
, система линейных уравнение имеет единственное решение, определяемое по формулам
Крамера:Пусть - определитель матрицы системы А,
-определитель, полученный из заменой j - го столбца столбцом свободных членов В.
Или в общем случае, для системы из n уравнений с n неизвестными:
Слайд 29Пример: Решить систему уравнений
по формулам Крамера.
значит система
имеет единственное решение, определяемое формулами Крамера
Слайд 30Рассмотрим систему линейных уравнений
где числа а11, а12,…а33 – коэффициенты системы,
b1,
b2,b3 - свободные члены системы,
х1, х2,х3 - неизвестные.
Расширенная матрица системы
Слайд 31Метод Гаусса решения систем линейных уравнений
Следующие действия над расширенной матрицей
системы называются элементарными преобразованиями.
Умножение или деление элементов строк на
одно и то же число, не равное нулю Перестановка местами двух строк
Прибавление к элементам строки элементов другой строки, умноженных на произвольный множитель.
Суть метода: с помощью элементарных преобразований над строками расширенная матрица приводится к треугольному виду.
Слайд 32Пример: Решить систему уравнений
методом Гаусса.
Расширенная матрица системы
имеет вид:
Переставим строки (для удобства):
От третьей строки отнимем первую, умноженную
на 4:к третьей строке прибавим
вторую, умноженную на 6
Слайд 33Матрица приведена к треугольному виду, ей соответствует преобразованная система уравнений:
Находим
решение этой системы, начиная с последнего уравнения:
третью строку разделим на
(-11)
