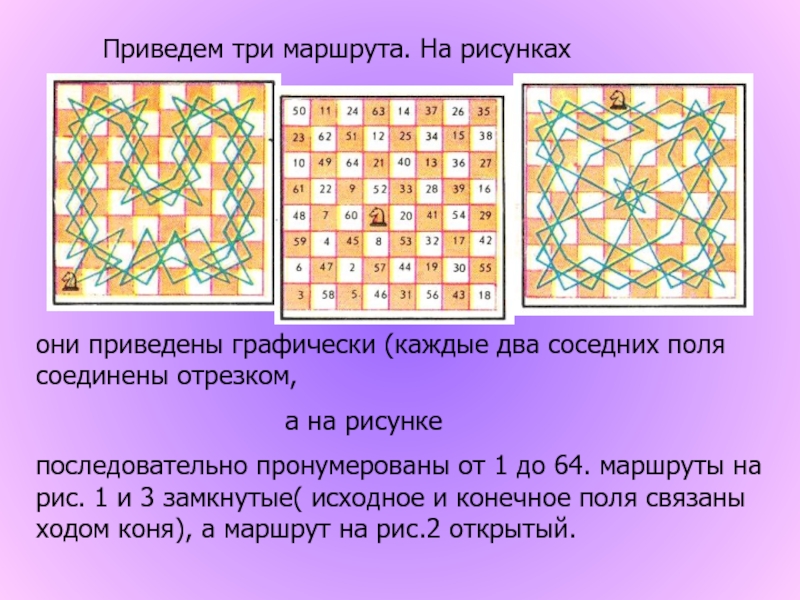
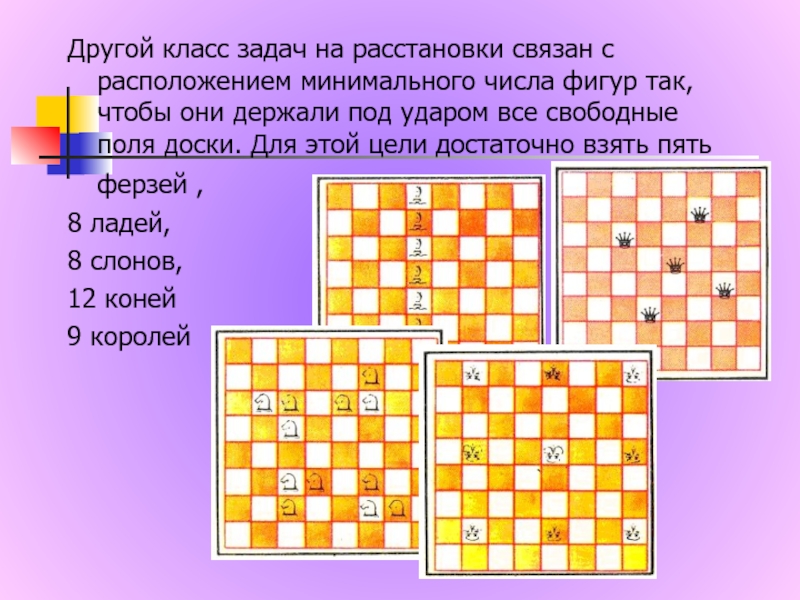
интересных математических задач. Не случайно шахматные термины можно встретить в
литературе по комбинаторике , теории графов, кибернетике, теории игр, программированию . Расскажем о нескольких математических задачах на шахматной доске.Задача 1.
Обойти конем все поля доски,
посетив каждое из них по од-
ному разу.
Этой задачей занимался Л.Эйлер