Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Матрицы
Содержание
- 1. Матрицы
- 2. Определители и матрицы1.Теоретическая часть2.Задачи3.Решения задач
- 3. Определители и матрицы1.Виды матриц2.Операции над матрицами3.Обратная матрица4.Решение матричных уравнений5.Ранг матрицыОглавление
- 4. 1. Виды матриц
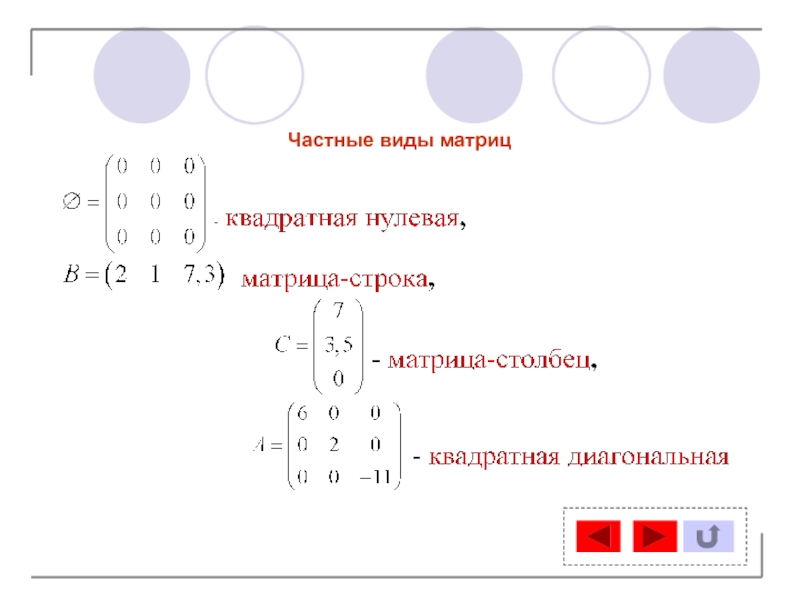
- 5. Частные виды матриц
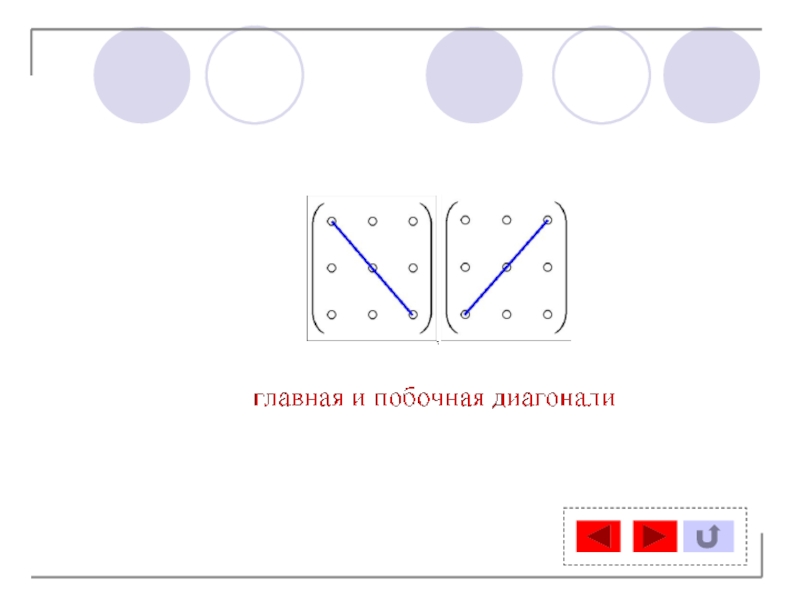
- 6. Слайд 6
- 7. Слайд 7
- 8. 2. Операции на матрицами
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. 3. Обратная матрица
- 14. Определители и матрицыОглавление
- 15. Слайд 15
- 16. Слайд 16
- 17. 4. Решение матричных уравнений
- 18. Слайд 18
- 19. 4. Ранг матрицы
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Задача №:
- 26. Задача 1Ответ:Просмотр решения
- 27. Задача 2Ответ:Просмотр решенияНайдите
- 28. Задача 3Ответ:Просмотр решенияНайдите 3А+2В, если
- 29. Задача 4Ответ:Просмотр решения
- 30. Задача 5Ответ:Просмотр решенияНайдите С = АВ, если
- 31. Задача 6Ответ:Просмотр решенияНайдите С = АВ, если
- 32. Найдите АВ и ВА, если Задача 7Ответ:Просмотр решения
- 33. Найдите все матрицы, перестановочные с матрицей Задача 8Ответ:Просмотр решения
- 34. Найдите матрицу, обратную для матрицы Задача 9Ответ:Просмотр решения
- 35. Задача 10Ответ:Просмотр решенияМетодом присоединенной матрицы найдите матрицу, обратную к матрице
- 36. Задача 11Ответ:Просмотр решенияМетодом элементарных преобразований строк найдите матрицу, обратную к матрице
- 37. Решите матричное уравнение , где Задача 12Ответ:Просмотр решения
- 38. Задача 13Ответ:Просмотр решенияРешите матричное уравнение , где
- 39. Задача 14Ответ: 2Просмотр решенияНайдите ранг матрицы
- 40. методом элементарных преобразований.Задача 15Ответ: 2Просмотр решенияНайдите ранг матрицы
- 41. Задача 16Ответ: 4Просмотр решенияНайдите ранг матрицы
- 42. Определители и матрицыРешение задачи №:Оглавление
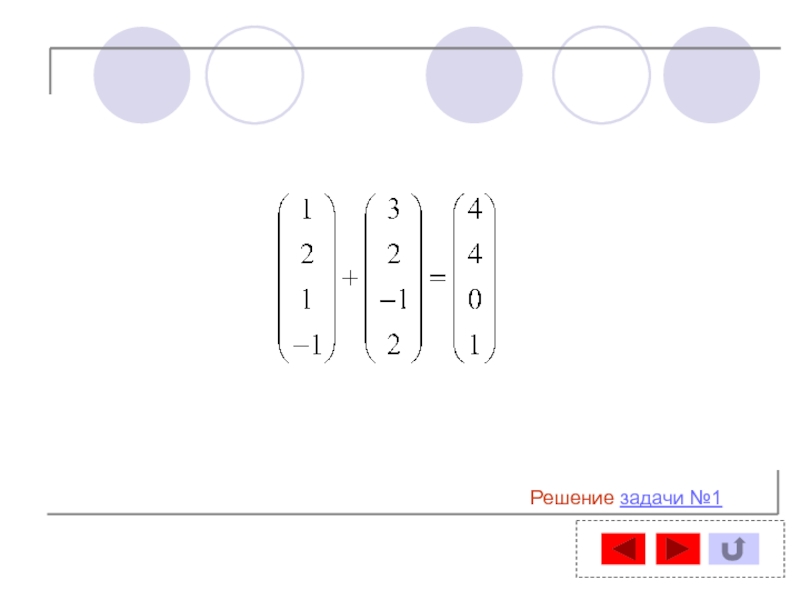
- 43. Решение задачи №1
- 44. Решение задачи №2
- 45. Решение задачи №3
- 46. Решение задачи №4Размерность матрицы А (23), размерность
- 47. Решение задачи №5
- 48. Решение задачи №6( размерность матрицы C )
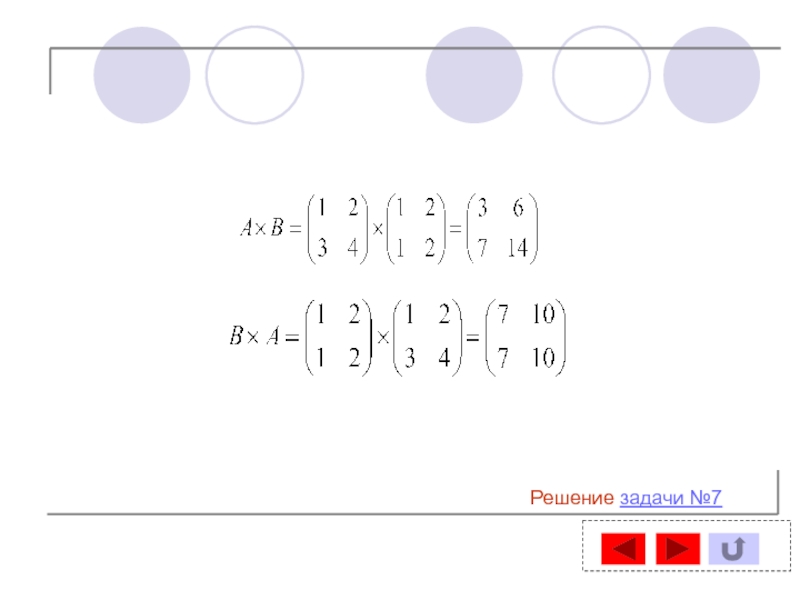
- 49. Решение задачи №7
- 50. Решение задачи №8Запишем вторую матрицу в виде
- 51. Решение задачи №9Проверка:
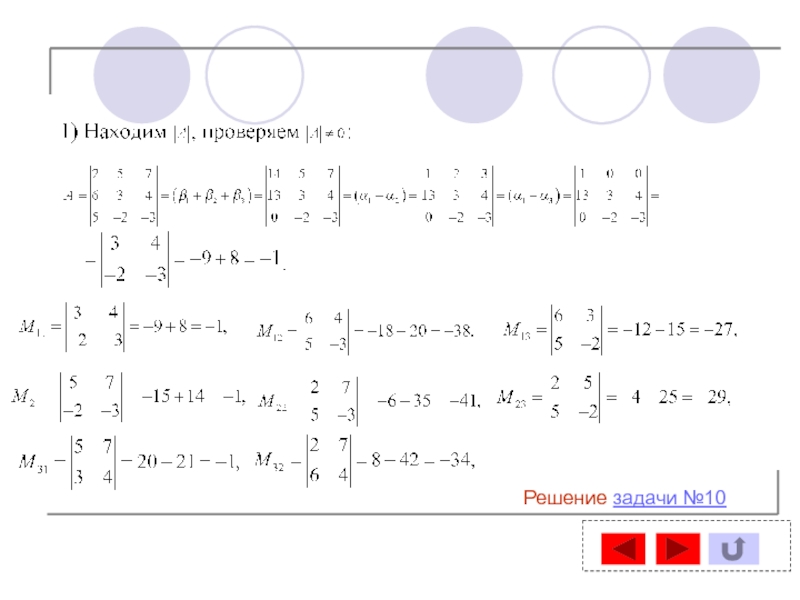
- 52. Решение задачи №10
- 53. Решение задачи №10
- 54. Решение задачи №10
- 55. Решение задачи №11Составляем и преобразуем вспомогательную матрицу :
- 56. Решение задачи №12Вычислим , значит, матрица A
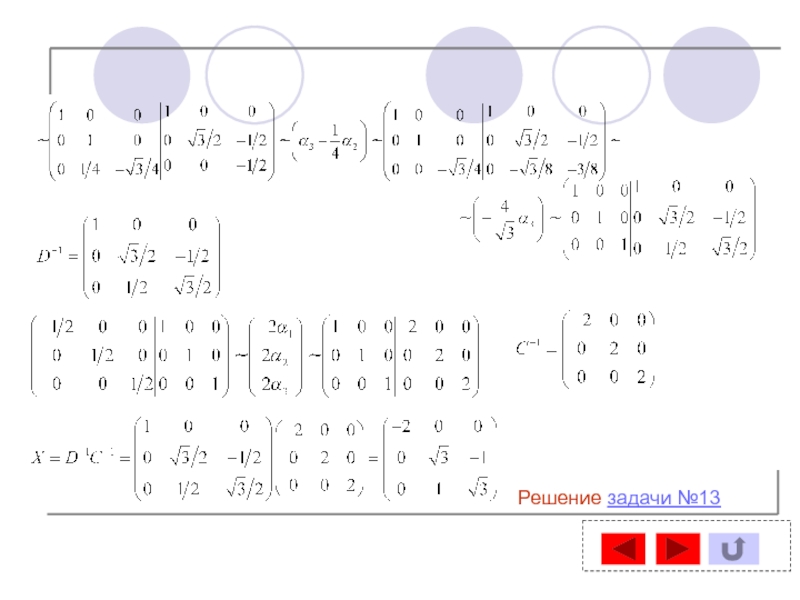
- 57. Решение задачи №13Вычислим и
- 58. Решение задачи №13
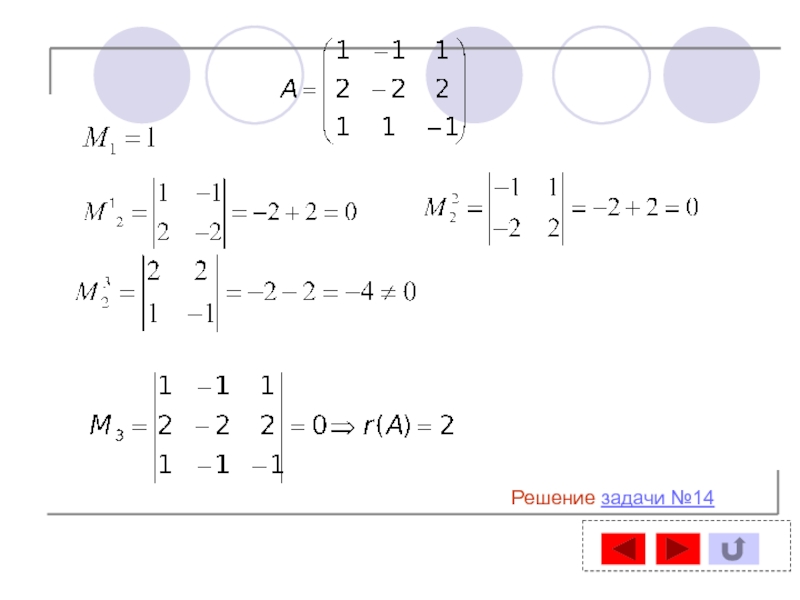
- 59. Решение задачи №14
- 60. Решение задачи №15rang A = 2.
- 61. Решение задачи №16 В левом верхнем углу
- 62. Скачать презентанцию
Определители и матрицы1.Теоретическая часть2.Задачи3.Решения задач
Слайды и текст этой презентации
Слайд 3Определители и матрицы
1.Виды матриц
2.Операции над матрицами
3.Обратная матрица
4.Решение матричных уравнений
5.Ранг матрицы
Оглавление
Слайд 35Задача 10
Ответ:
Просмотр решения
Методом присоединенной матрицы найдите матрицу,
обратную к матрице
Слайд 36Задача 11
Ответ:
Просмотр решения
Методом элементарных преобразований строк найдите
матрицу, обратную к
матрице
Слайд 46Решение задачи №4
Размерность матрицы А (23), размерность матрицы В (32),
число столбцов матрицы А совпадает с числом строк матрицы В,
в результате получится матрица С, размерность которой (22).
Слайд 50Решение задачи №8
Запишем вторую матрицу в виде
и найдем
произведения
и
:
где a и m – произвольные
числа.
Слайд 56Решение задачи №12
Вычислим
, значит, матрица A – невырожденная.
Построим
матрицу A–1 , обратную матрице A, (любым из двух способов)
:1.Метод присоединенной матрицы:
2.Метод элементарных преобразований строк:
Записываем решение матричного уравнения:
Слайд 61Решение задачи №16
В левом верхнем углу матрицы стоит определитель
треугольного вида, который равен произведению элементов,
стоящих на его
главной диагонали , значит ранг матрицы равен четырем. 
