Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
Содержание
- 1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 2. Матрица:Размерность матрицы: Элемент матрицы:
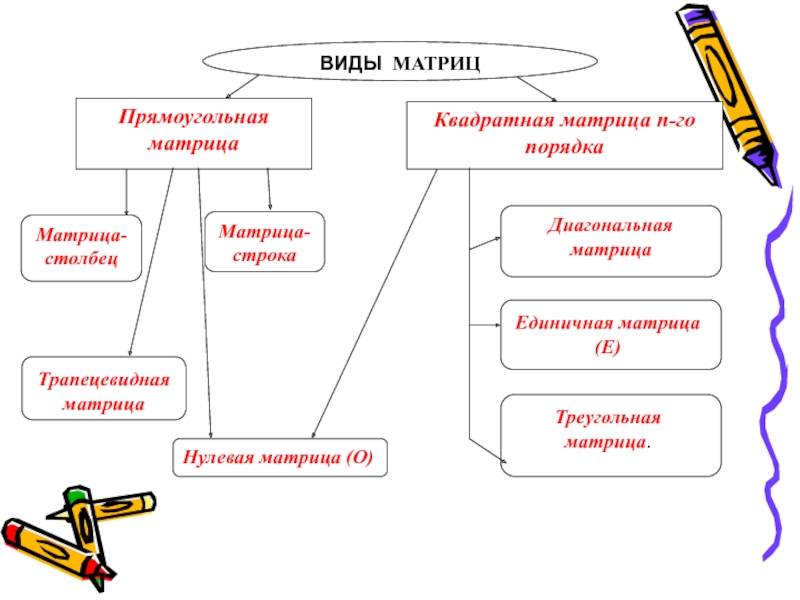
- 3. Квадратная матрица n-го порядкаПрямоугольная матрицаВИДЫ МАТРИЦМатрица-столбецМатрица-строкаНулевая матрица (О) Диагональная матрица Трапецевидная матрицаЕдиничная матрица (Е)Треугольная матрица.
- 4. Слайд 4
- 5. Слайд 5
- 6. ДЕЙСТВИЯ НАД МАТРИЦАМИ:умножение матрицы на
- 7. Умножение матрицы на действительное число∙А = А
- 8. А + В = С (А –
- 9. Слайд 9
- 10. Умножение матрицА В = С где
- 11. Слайд 11
- 12. Формула и схема вычисления элемента c11
- 13. Слайд 13
- 14. А A A
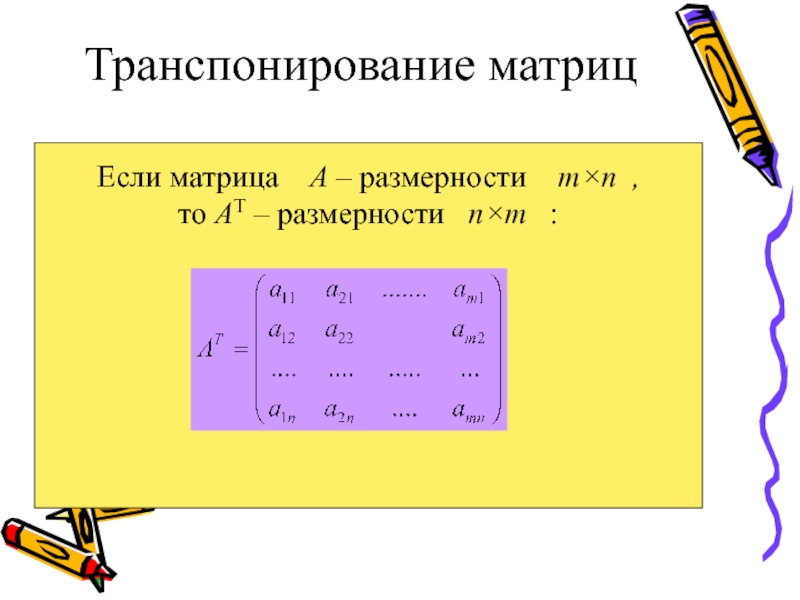
- 15. Если матрица A – размерности
- 16. Спасибо за внимание!!! =)
- 17. Скачать презентанцию
Матрица:Размерность матрицы: Элемент матрицы:
Слайды и текст этой презентации
Слайд 3Квадратная матрица n-го порядка
Прямоугольная матрица
ВИДЫ МАТРИЦ
Матрица-столбец
Матрица-строка
Нулевая матрица (О)
Диагональная матрица
Слайд 6ДЕЙСТВИЯ НАД МАТРИЦАМИ:
умножение матрицы на действительное число;
сложение и
вычитание матриц;
умножение матрицы на матрицу;
возведение матрицы в степень;
транспонирование.
Слайд 7Умножение матрицы на действительное число
∙А = А ∙ = С
где
А – матрица произвольной размерности
И
Слайд 8А + В = С
(А – В = С),
где
А, В – матрицы одинаковой размерности и
Сложение (вычитание) матриц
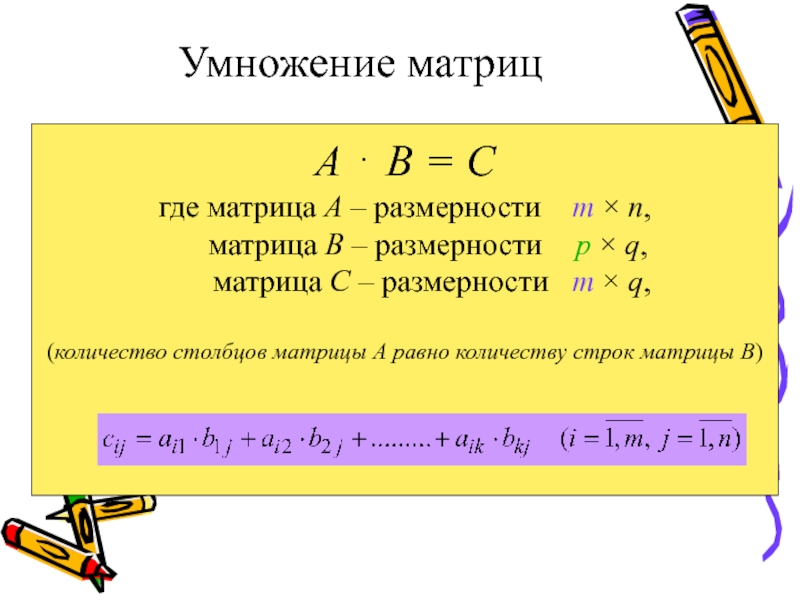
Слайд 10Умножение матриц
А В = С
где матрица А –
размерности m n, матрица В
– размерности p q,матрица С – размерности m q,
(количество столбцов матрицы А равно количеству строк матрицы В)
и
Слайд 14А A A = Ak
,
где А – квадратная матрица,
в частности А A
=A2,
А A A = A3 Возведение матриц
в степень