Слайд 2Основные сведения
о матрицах
Слайд 3Понятие матрицы
Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m
строк и n столбцов.
Обозначение матриц: A, B, C, X, …
Числа,
составляющие матрицу, называются элементами матрицы.
Обозначение элементов:
где i – номер строки, j – номер столбца
Слайд 4Запись матриц
В общем виде
В сокращенной форме
Слайд 6Виды матриц
Определение: Матрица любого размера называется нулевой или нуль-матрицей, если
все ее элементы равны нулю.
Обозначение: О
Пример:
Слайд 7Виды матриц
Матрица, размерности:
1×n называется матрицей-строкой или вектором-строкой
m×1 называется матрицей-столбцом или
вектором-столбцом
Слайд 8Виды матриц
Матрица размерности n×n называется квадратной порядка n
Пример
- квадратная
матрица второго порядка
Слайд 9Диагональ матрицы
Элементы матрицы, у которых номер столбца равен номеру строки
(i=j), называются диагональными и составляют главную диагональ матрицы.
Сумма элементов главной
диагонали квадратной матрицы называется её следом. Обозначается trA.
Слайд 10Виды квадратных матриц
Квадратная матрица, у которой все недиагональные элементы равны
нулю, называется диагональной матрицей.
Пример:
- диагональная матрица
второго порядка
Слайд 11Виды квадратных матриц
Если у диагональной матрицы порядка n все диагональные
элементы равны 1, матрица называется единичной порядка n.
Обозначение En
Пример
- единичная
матрица
третьего порядка
Слайд 14Операции над матрицами
Умножение матрицы на число
Сложение матриц
Вычитание матриц
Умножение матриц
Возведение в
степень
Транспонирование матрицы
Слайд 15Умножение матрицы на число
Выполнимо для любых матриц и любых чисел
Производится
поэлементно
Правило:
Пример:
Слайд 16Сложение матриц
Выполнимо только для матриц одинаковой размерности
Производится поэлементно
Правило:
Пример:
Слайд 17Вычитание матриц
Выполнимо только для матриц одинаковой размерности
Производится поэлементно
Правило:
или
Пример:
Слайд 18Умножение матриц
Выполнимо если число столбцов первого множителя равно числу строк
второго
Правило:
Примеры:
Слайд 19Возведение в степень
Выполнимо для квадратных матриц
Правила:
Пример:
Слайд 20Транспонирование
Выполнимо для любой матрицы
Обозначение: АТ или А'
Правило: поменять строки на
столбцы с сохранением порядка.
Пример:
Слайд 22Определитель матрицы
Любой квадратной матрице ставится в соответствие по определенному закону
некоторое число, называемое определителем или детерминантом.
Обозначение:
det A или |А|
или ∆А или ∆n или ∆
Определитель матрицы – это число.
Определитель существует только для квадратных матриц.
Слайд 23Определитель первого порядка
Определяется по формуле:
при А=(а11) ∆1=а11
Пример:
А=(-5) ∆1=
∆А = - 5
Слайд 24Определитель второго порядка
Определяется формулой:
Пример:
Слайд 25Определитель третьего порядка
Определяется формулой
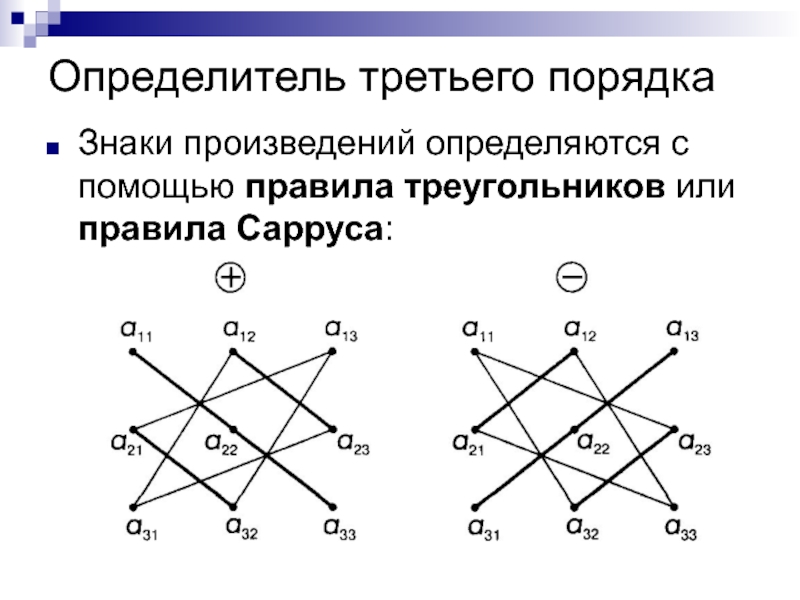
Слайд 26Определитель третьего порядка
Знаки произведений определяются с помощью правила треугольников или
правила Сарруса:
Слайд 27Определитель n-го порядка
Определителем матрицы А n-го порядка называется алгебраическая сумма
n! произведений n-го порядка элементов этой матрицы, причем в каждое
произведение входит по одному элементу из каждой строки и каждого столбца данной матрицы
Слайд 28Минор
Рассмотрим квадратную матрицу Аn
Минором называется определитель (n-1)-го порядка, полученный
вычеркиваем из матрицы А i-й строки и j-го столбца.
Пример:
Слайд 29Алгебраическое дополнение
Алгебраическим дополнением называется минор , взятый
со знаком , т.е.
Пример
Матрица, составленная из алгебраических дополнений элементов
матрицы А, называется присоединенной матрицей и обозначается
Слайд 30Теорема Лапласа
Определитель равен сумме произведений элементов любой строки (столбца) на
их алгебраические дополнения:
- разложение определителя по элементам i-й строки
Используется для
вычисления определителей порядка выше третьего.
Слайд 31Теорема Лапласа (пример)
Вычислить
Решение:
Слайд 32Свойства определителей
При транспонировании ∆ не меняется.
При перестановке двух строк ∆
меняет знак.
∆=0 если:
содержит нулевую строку (столбец);
содержит две одинаковые строки;
содержит две
пропорциональные строки.
Если все элементы строки умножить на число λ, то ∆ увеличится в λ раз; общий множитель строки можно вынести за знак ∆.
Если к элементам строки прибавить элементы другой строки, умноженной на число ≠0, то ∆ не меняется.
Слайд 33Свойства определителей
Определитель треугольной матрицы равен произведению ее диагональных элементов.
Определитель диагональной
матрицы равен произведению ее диагональных элементов
Слайд 34Способы вычисления определителей
Перебором всевозможных произведений (по определению);
Разложением по строке или
столбцу (по теореме Лапласа);
С использованием свойств определителей;
Сочетание способов.
Слайд 35Обратная матрица
Обозначение: А-1–обратная для матрицы А
Определение: Матрицей А-1, обратной к
данной квадратной матрице А, называется такая, что выполняется равенство:
А-1∙А
= А∙ А-1 = Е.
Пример: -обратна матрице ,
т.к.
Слайд 36Обратимость матрицы
Если определитель квадратной матрицы равен нулю (∆А=0), матрица называется
вырожденной.
Если определитель отличен от нуля (∆А≠0), матрица называется невырожденной.
Критерий
обратимости матрицы:
А имеет обратную ↔ А – невырожденная
Обратную матрицу можно найти по формуле:
Слайд 37Алгоритм нахождения
обратной матрицы
Вычислить ∆А. Если ∆А=0, то А-1 не
существует.
Если ∆А≠0, найти алгебраические дополнения всех элементов. Составить
Транспонировать матрицу
Выполнить умножение
на
Выполнить проверку равенства А-1∙А = Е.
Слайд 38Нахождение обратной матрицы (пример)
Найти матрицу, обратную к
Решение:
1. ∆А =
-1∙1 - 2∙0 = -1 ≠0 → А-1 существует.
2.
Итак,
3.
Слайд 39Нахождение обратной матрицы (пример)
4.
5. Проверка:
Ответ:
Слайд 40Ранг матрицы
Определение: Рангом матрицы называется наивысший порядок отличных от нуля
миноров этой матрицы.
Обозначение: rang A или r(A).
Ранг матрицы показывает число
ее линейно независимых строк (столбцов).
Слайд 41Основные свойства ранга
Ранг матрицы не превосходит меньшего из ее размеров:
для Аm×n r(A) ≤ min {m, n};
Ранг матрицы равен нулю
только для нулевой матрицы:
r(A)=0 ↔ A=O;
Ранг квадратной матрицы равен ее порядку только для невырожденной матрицы:
для Аn r(A)=n ↔ А – невырожденная;
Ранг матрицы не меняется при элементарных преобразованиях над её строками (столбцами).