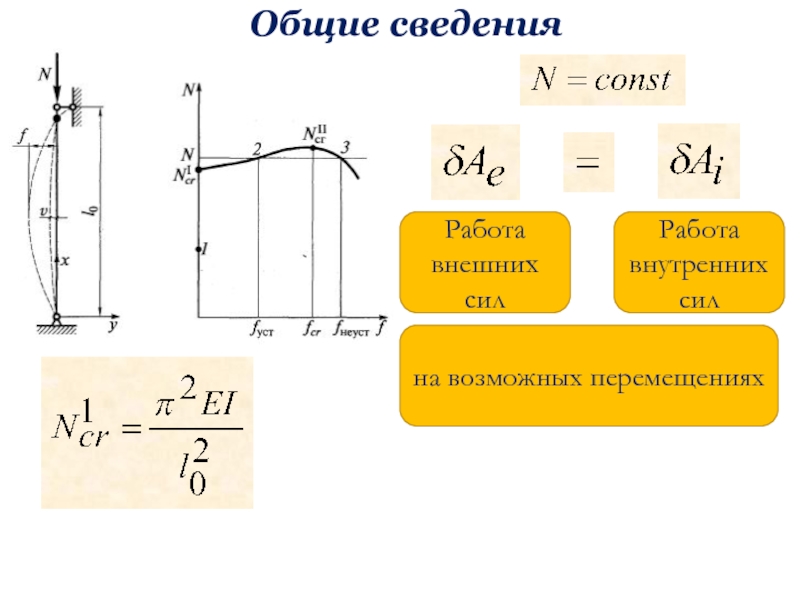
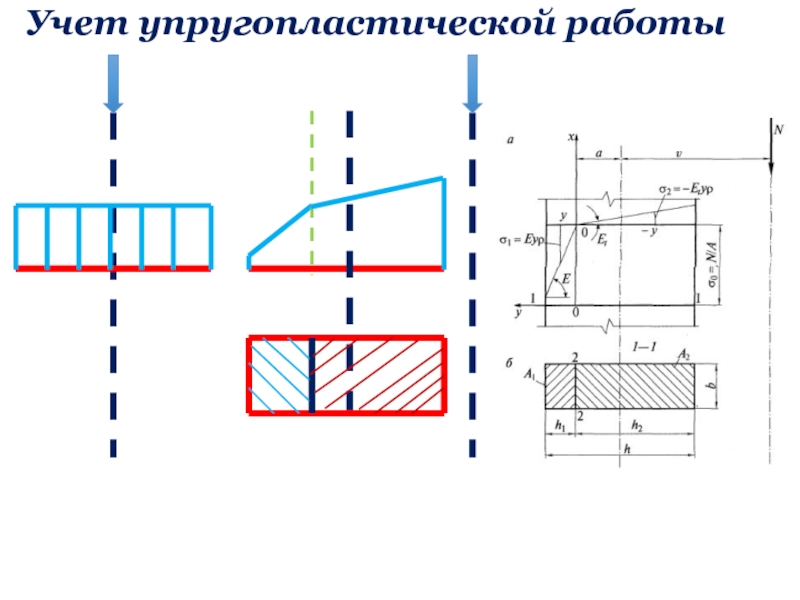
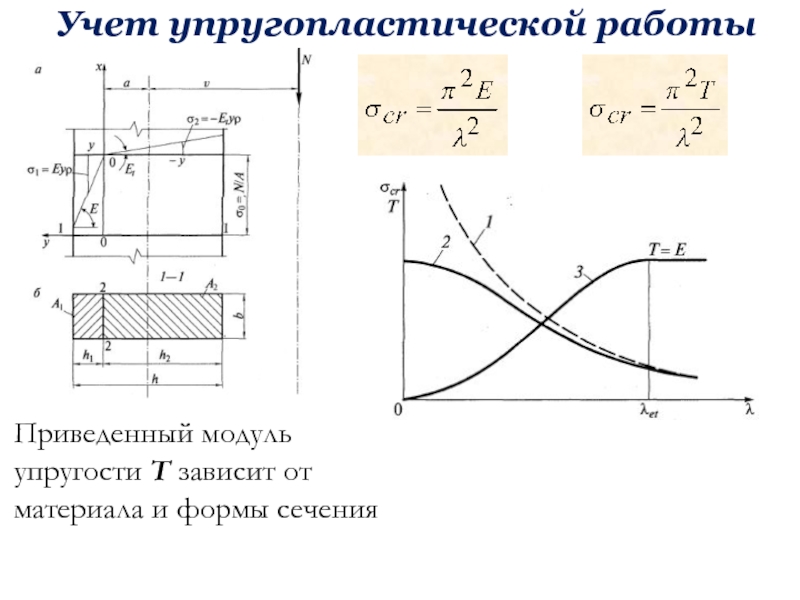
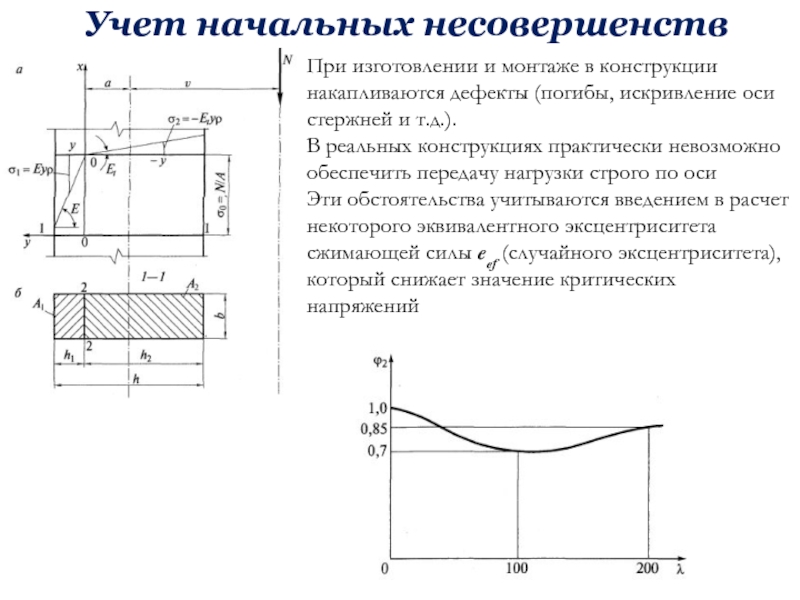
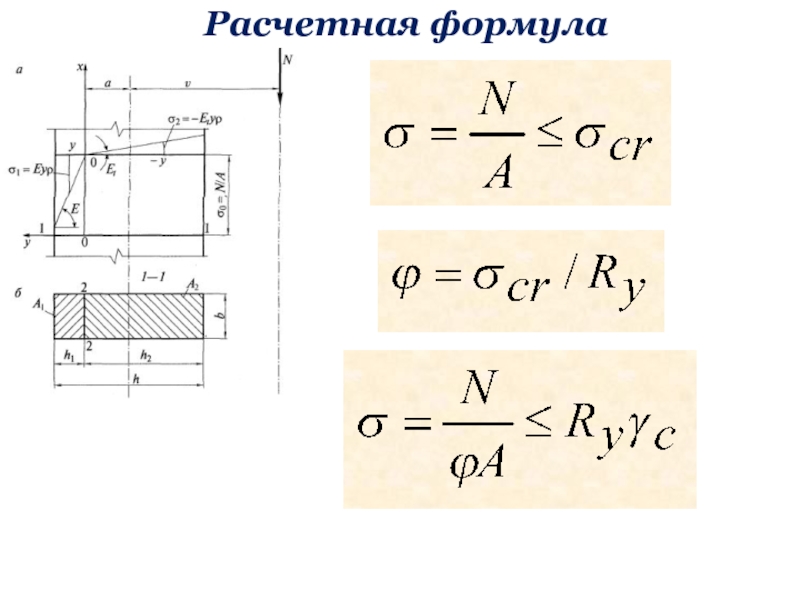
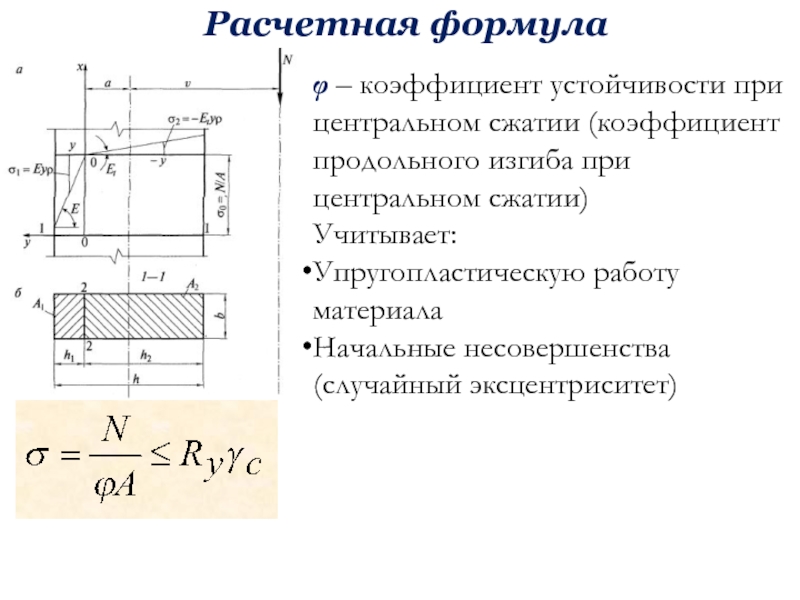
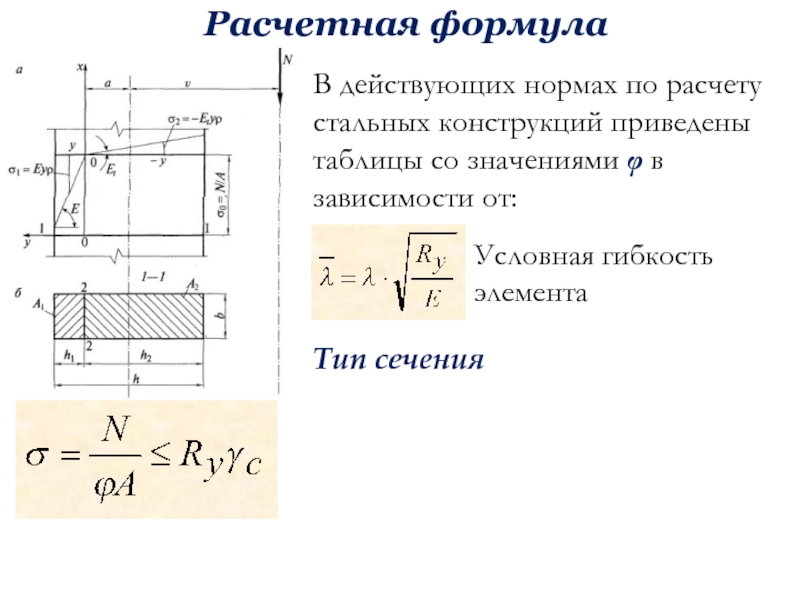
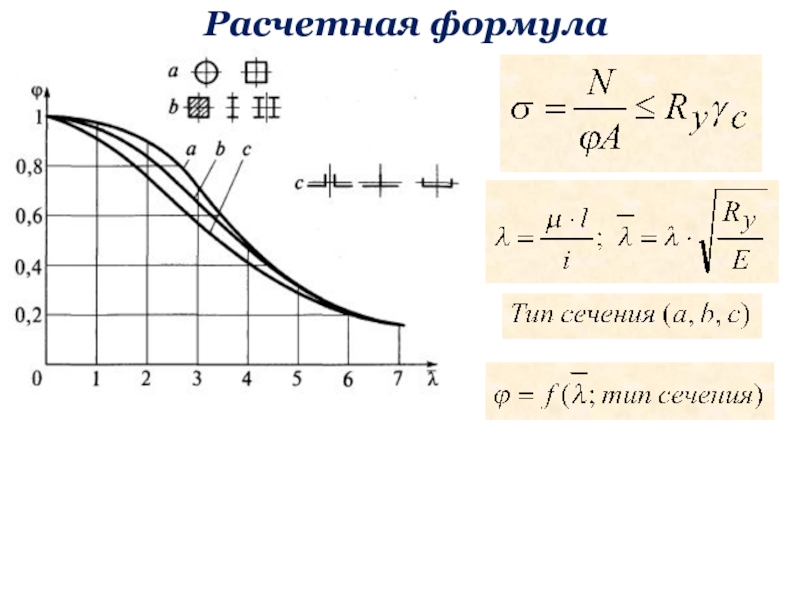
бюджетное образовательное учреждение высшего образования «Уфимский государственный нефтяной технический университет»
Архитектурно-строительный
институтКафедра Строительные конструкции
Порываев Илья Аркадьевич – к.т.н. доцент



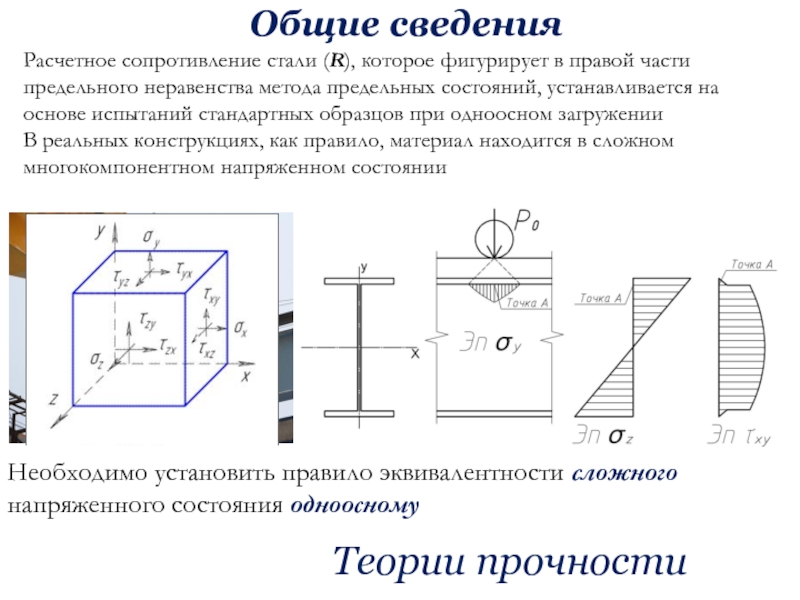

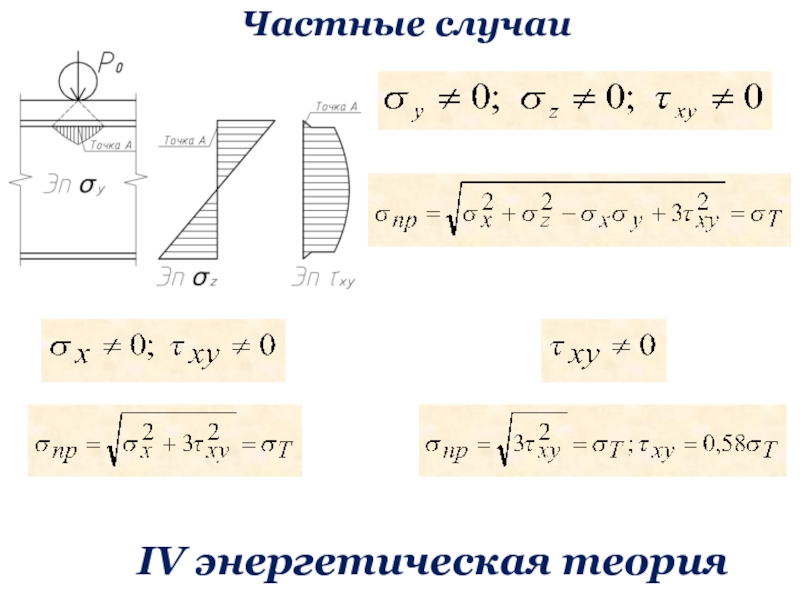


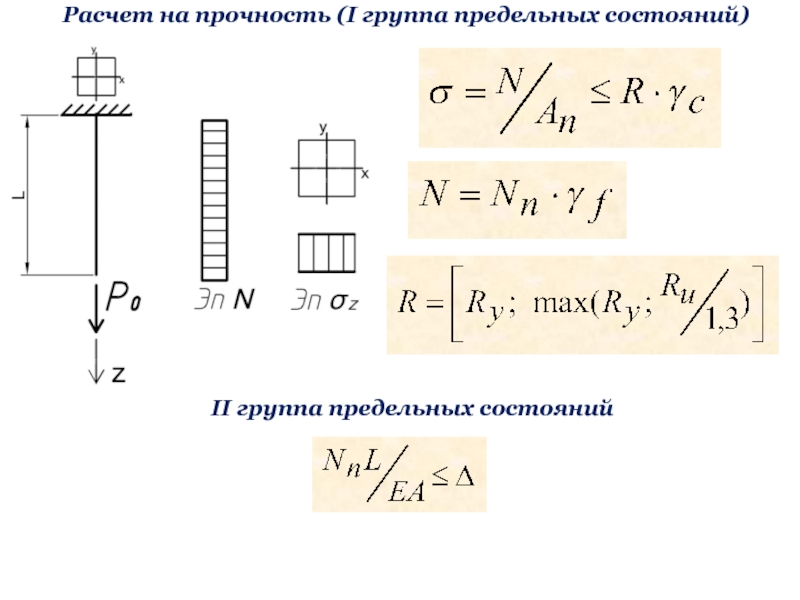


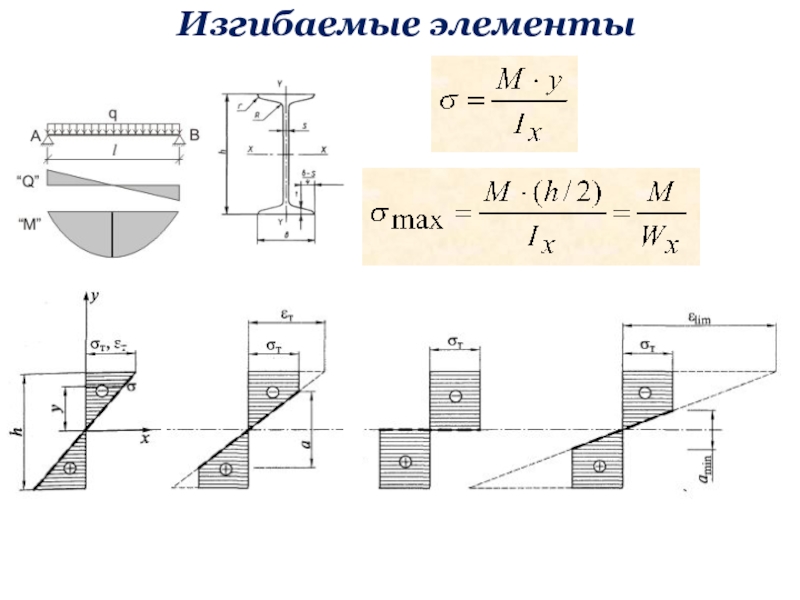
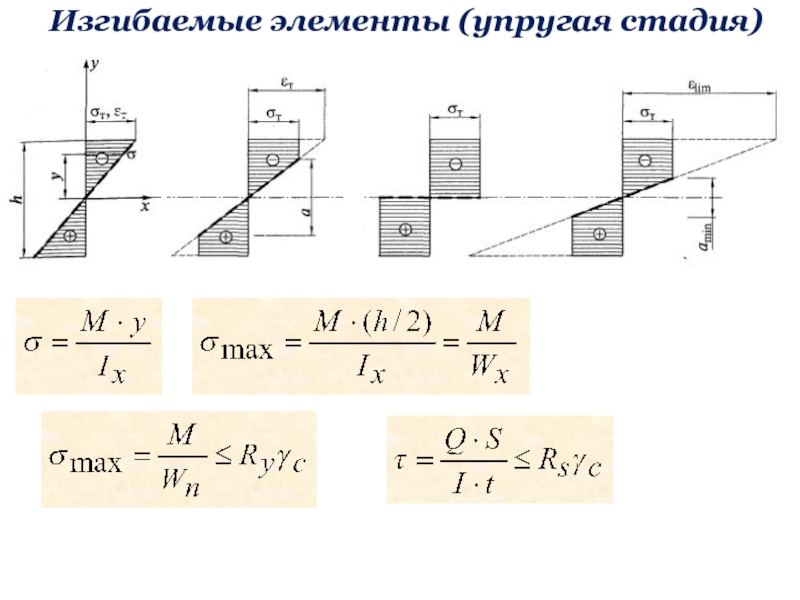
![Металлические конструкции, включая сварку Часть 1 Элементы и соединения Изгибаемые элементы (II группа предельных состояний)[f] – предельно допускаемый прогиб балки, Изгибаемые элементы (II группа предельных состояний)[f] – предельно допускаемый прогиб балки, который выражается в долях от пролета](/img/thumbs/9b28c73c698ac7e36b338e398d71f88e-800x.jpg)