Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод аналіза ієрархій Зміст лекції
Содержание
- 1. Метод аналіза ієрархій Зміст лекції
- 2. Лекція4. Метод аналіза ієрархій
- 3. Розглядається підхід до прийняття рішень в ситуаціях,
- 4. Теоретико-системные основы математического моделирования (с) Н.М. Светлов, 2006/20 Приклад багатокритеріального експертного оцінювання альтернатив
- 5. Приклад багатокритеріального експертного оцінювання альтернатив Приклад. Мартін
- 6. Приклад багатокритеріального експертного оцінювання альтернатив Приклад. Мартін
- 7. Приклад багатокритеріального експертного оцінювання альтернатив Задача має
- 8. Приклад багатокритеріального експертного оцінювання альтернатив Завдання на
- 9. 2. Багатокритеріальне експертне оцінювання альтернатив Приклад розширеної ієрархії прийняття рішень.Теорія Прийняття рішень © ЄА. Лавров, 2014-2019/100
- 10. 2.Багатокритеріальне експертне оцінювання
- 11. 2.Багатокритеріальне експертне оцінювання
- 12. 2.Багатокритеріальне експертне оцінювання
- 13. 2.Багатокритеріальне експертне оцінювання
- 14. Приклад багатокритеріального експертного оцінювання альтернатив Завдання на
- 15. 2.Багатокритеріальне експертне оцінювання
- 16. 2.Багатокритеріальне експертне оцінювання альтернатив.
- 17. 3.Cпособи визначення вагових коефіцієнтівТеорія Прийняття рішень © ЄА. Лавров, 2014-2019/14
- 18. 3.Cпособи визначення вагових коефіцієнтів
- 19. 3.Cпособи визначення вагових коефіцієнтів
- 20. 3.Cпособи визначення вагових
- 21. 3.Cпособи визначення вагових
- 22. 3.Cпособи визначення вагових
- 23. 3.Cпособи визначення вагових
- 24. 3.Cпособи визначення вагових
- 25. 3.Cпособи визначення вагових
- 26. 4.Узгодженість матриць порівняньТеорія Прийняття рішень © ЄА. Лавров, 2014-2019/100
- 27. 4.Узгодженість матриць
- 28. 4.Узгодженість матриць
- 29. 4.Узгодженість матриць
- 30. 4.Узгодженість матриць
- 31. 4.Узгодженість матриць
- 32. 4.Узгодженість матриць
- 33. 4.Узгодженість матриць
- 34. 4.Узгодженість матриць
- 35. 4.Узгодженість матриць
- 36. 4.Узгодженість матриць
- 37. 4.Узгодженість матриць
- 38. 4.Узгодженість матриць
- 39. 4.Узгодженість матриць
- 40. 4.Узгодженість матриць
- 41. 5. Рішення задач методомАналіза ієрархій в ExcelТеорія Прийняття рішень © ЄА. Лавров, 2014-2019/100
- 42. 5. Рішення задач методомАналіза ієрархій в ExcelТеорія Прийняття рішень © ЄА. Лавров, 2014-2019/100
- 43. 5.Рішення задач методом Аналіза ієрархій в Excel
- 44. 5. Завдання на сам. роботуТеорія Прийняття рішень © ЄА. Лавров, 2014-2019/100
- 45. Теорія Прийняття рішень © ЄА. Лавров, 2014-2019/100
- 46. Теорія Прийняття рішень © ЄА. Лавров, 2014-2019/100
- 47. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Лекція4. Метод аналіза ієрархій
Зміст лекції:
Приклад багатокритеріального експертного оцінювання альтернатив
Багатокритеріальне експертне оцінювання альтернатив Приклад розширеної ієрархії прийняття рішень.
Cпособи визначення вагових коефіцієнтів в методі аналіза ієрархій
Узгодженість матриць порівнянь
Рішення задач методом Аналіза ієрархій в Excel
Завдання на сам. роботу.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/100
Слайд 3Розглядається підхід до прийняття рішень в ситуаціях, коли, наприклад,
для
ідей, почуттів, емоцій
визначаються деякі кількісні показники,
що забезпечують числову
шкалу переваг для можливих альтернативних рішень.Цей підхід відомий як
метод аналізу ієрархій.
Перед тим як викласти деталі даного методу, розглянемо приклад, що демонструє спосіб, за допомогою якого оцінюються різні альтернативні рішення.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 4Теоретико-системные основы математического моделирования
(с) Н.М. Светлов, 2006
/20
Приклад багатокритеріального експертного
оцінювання альтернатив
Слайд 5Приклад багатокритеріального експертного оцінювання альтернатив
Приклад. Мартін Ганс - випускник-відмінник середньої
школи, який
отримав повну стипендію від трьох університетів: А, В і
С.Для того
щоб вибрати університет, Альтернативи
Мартін сформулював два основних
критерії:
місцезнаходження університету
та його академічна репутація.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 6Приклад багатокритеріального експертного оцінювання альтернатив
Приклад. Мартін Ганс - випускник-відмінник середньої
школи, який
отримав повну стипендію від трьох університетів: А, В і
С. Для тогощоб вибрати університет, Мартін сформулював два основних
критерії: місцезнаходження університету та його академічна репутація.
Будучи відмінним учнем, він оцінює академічну репутацію університету в п'ять разів вище ніж його місцезнаходження. Це призводить до того, що репутації університету приписується вага приблизно 83%,
а місцезнохожденню- 17%.
Далі Мартін використовує системний аналіз для оцінки університетів з точки зору їх місцезнаходження та репутації.
Проведений аналіз дає такі оцінки..
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
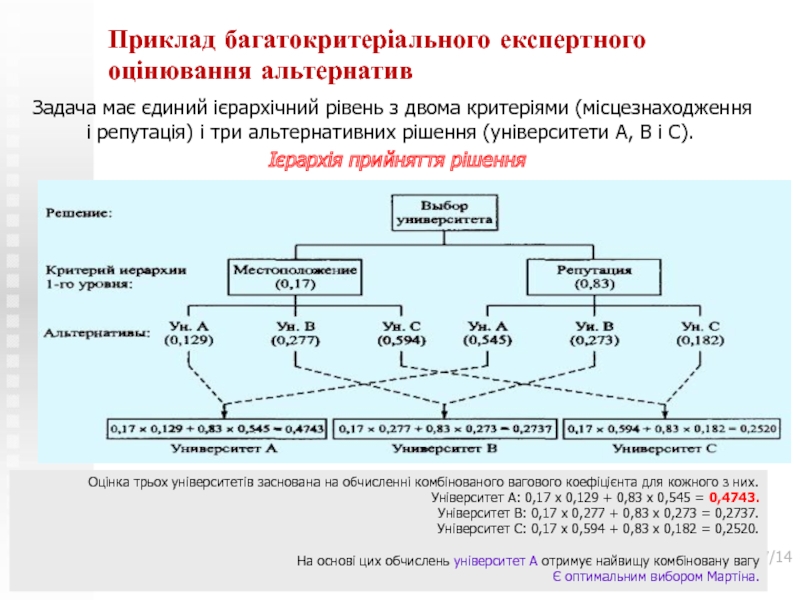
Слайд 7Приклад багатокритеріального експертного оцінювання альтернатив
Задача має єдиний ієрархічний рівень з
двома критеріями (місцезнаходження і репутація) і три альтернативних рішення (університети
А, В і С).Ієрархія прийняття рішення
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Оцінка трьох університетів заснована на обчисленні комбінованого вагового коефіцієнта для кожного з них.
Університет А: 0,17 х 0,129 + 0,83 х 0,545 = 0,4743.
Університет В: 0,17 х 0,277 + 0,83 х 0,273 = 0,2737.
Університет С: 0,17 х 0,594 + 0,83 х 0,182 = 0,2520.
На основі цих обчислень університет А отримує найвищу комбіновану вагу
Є оптимальним вибором Мартіна.
Слайд 8Приклад багатокритеріального експертного оцінювання альтернатив
Завдання на самост. Роботу. 1.
1.Скласти задачу
вибору альтернативи
(вибір
покупки
Теми наук. Роботи
Наук керівника
Місця роботи
Місця відпочику
Інше)
2. Задати дані
3.
Вірішити задачу вибору_________________________________
Виконується в Конспекті
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
.
Слайд 9
2. Багатокритеріальне експертне оцінювання альтернатив Приклад розширеної ієрархії прийняття рішень.
Теорія
Прийняття рішень
© ЄА. Лавров, 2014-2019
/100
Слайд 10
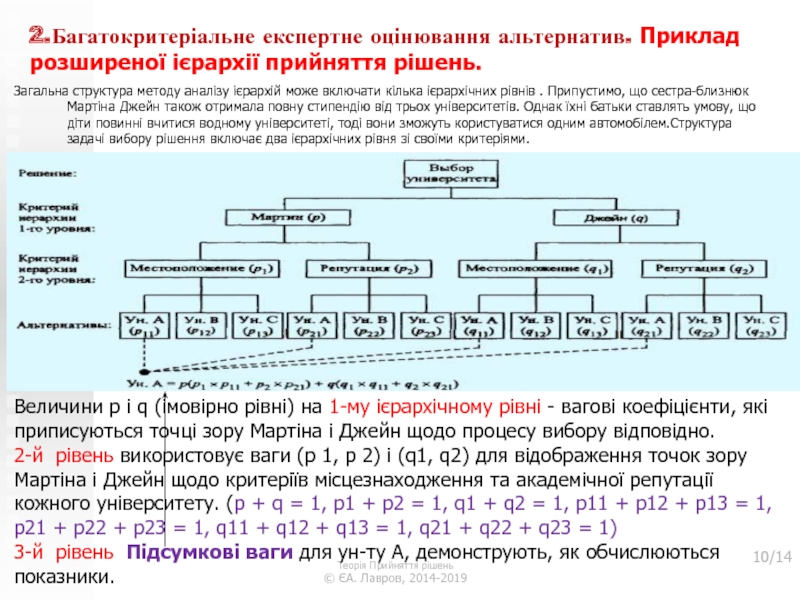
2.Багатокритеріальне експертне оцінювання альтернатив. Приклад розширеної ієрархії прийняття рішень.
Загальна структура
методу аналізу ієрархій може включати кілька ієрархічних рівнів . Припустимо,
що сестра-близнюк Мартіна Джейн також отримала повну стипендію від трьох університетів. Однак їхні батьки ставлять умову, що діти повинні вчитися водному університеті, тоді вони зможуть користуватися одним автомобілем.Структура задачі вибору рішення включає два ієрархічних рівня зі своїми критеріями.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Величини р і q (імовірно рівні) на 1-му ієрархічному рівні - вагові коефіцієнти, які приписуються точці зору Мартіна і Джейн щодо процесу вибору відповідно.
2-й рівень використовує ваги (р 1, р 2) і (q1, q2) для відображення точок зору Мартіна і Джейн щодо критеріїв місцезнаходження та академічної репутації кожного університету. (p + q = 1, p1 + p2 = 1, q1 + q2 = 1, p11 + p12 + p13 = 1, p21 + p22 + p23 = 1, q11 + q12 + q13 = 1, q21 + q22 + q23 = 1)
3-й рівень Підсумкові ваги для ун-ту А, демонструють, як обчислюються показники.
Слайд 11
2.Багатокритеріальне експертне оцінювання альтернатив. Приклад розширеної ієрархії прийняття рішень.Завдання.
Завдання 1
Нехай для задачі вибору університету Мартіном і Джейн встановлені наступні
значення вагових коефіцієнтівТеорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Завдання на сам. Роботу 2. Нехай для задачі вибору університету Мартіном і Джейн встановлені наступні значення вагових коефіцієнтів
р=0,5, q=0,5,
p1=0,17, p2=0,83,
p11=0,129, p12=0,277, p13=0,594,
p21=0,545, p22=0,273, p23=0,182,
q1=0,3, q2=0,7,
q11=0,2, q12=0,3, q13=0,5,
q21=0,5, q22=0,2, q23=0,3,
Задача- вибрати університет
Слайд 12
2.Багатокритеріальне експертне оцінювання альтернатив. Приклад розширеної ієрархії прийняття рішень.
Завдання 1
Нехай для задачі вибору університету Мартіном і Джейн встановлені наступні
значення вагових коефіцієнтівТеорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Рішення
Університет А: p(p1*p11+p2*p21)+q(q1*q11+q2*q21) = 0,5(0,17*0,129+0,83*0,545)+0,5(0,3*0,2+0,7*0,5) = 0,44214
Університет B: p(p1*p12+p2*p22)+q(q1*q12+q2*q22) = 0,5(0,17*0,277+0,83*0,273)+0,5(0,3*0,3+0,7*0,2) = 0,25184
Університет C: p(p1*p13+p2*p23)+q(q1*q13+q2*q23) = 0,5(0,17*0,594+0,83*0,182)+0,5(0,3*0,5+0,7*0,3) = 0,30602___________________________________________
Університет А отримує найвищу комбіновану вагу і, отже, є оптимальним вибором.
Слайд 13
2.Багатокритеріальне експертне оцінювання альтернатив. Приклад розширеної ієрархії прийняття рішень.Завдання.
Завдання 1
Нехай для задачі вибору університету Мартіном і Джейн встановлені наступні
значення вагових коефіцієнтівТеорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Завдання на сам. Роботу 2 Продовження
. р=0,5, q=0,5,
p1=0,17, p2=0,83,
p11=0,129, p12=0,277, p13=0,594,
p21=0,545, p22=0,273, p23=0,182,
q1=0,3, q2=0,7,
q11=0,2, q12=0,3, q13=0,5,
q21=0,5, q22=0,2, q23=0,3,
Для кожного показника p1, p2,…..
Дати змістовний опис його Сутності.
Слайд 14Приклад багатокритеріального експертного оцінювання альтернатив
Завдання на самост. Роботу. 3
(аналог задачі
2,
але – з врахуванням вимог 2-х учасників)
1.Скласти задачу вибору
альтернативи(вибір
покупки
Місця відпочику
Інше)
2. Задати дані
3. Вірішити задачу вибору
_________________________________
Виконується в Конспекті
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
.
Слайд 15
2.Багатокритеріальне експертне оцінювання альтернатив.
?
Які Складності і проблеми підходу?
Теорія Прийняття
рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 16
2.Багатокритеріальне експертне оцінювання альтернатив.
Теорія Прийняття рішень
© ЄА. Лавров,
2014-2019
/14
Складність методу аналізу ієрархій-
у визначенні
відносних вагових коефіцієнтів для оцінки альтернатив
Слайд 17
3.Cпособи визначення вагових коефіцієнтів
Теорія Прийняття рішень
© ЄА. Лавров,
2014-2019
/14
Слайд 18
3.Cпособи визначення вагових коефіцієнтів
Теорія Прийняття рішень
© ЄА. Лавров,
2014-2019
/14
Якщо задано n критеріїв на заданому рівні ієрархії,
Створюється матриця
А розмірності n,( називається матрицею парних порівнянь)
відображає судження ОПР , щодо важливості різних критеріїв.
Парне порівняння виконується таким чином, що
критерій в рядку i (i = 1, 2, ..., n)
оцінюється щодо кожного
з критеріїв,
представлених n стовпцями.
Позначимо через aij елемент матриці А, що знаходиться на перетині i-го рядка і j-го стовпця.
Відповідно до методу аналізу ієрархій для опису згаданих оцінок використовуються цілі числа від 1 до 9.
При цьому: aij = 1 означає, що i-й і j-й критерії однаково важливі, aij = 5 відображає думку, що i-й критерій значно важливіше, ніж j-й, aij = 9 вказує, що i-й критерій надзвичайно важливіше j-го.
Слайд 19
3.Cпособи визначення вагових коефіцієнтів
Теорія Прийняття рішень
© ЄА.
Лавров, 2014-2019
/14
Позначимо через aij елемент матриці А,
що знаходиться на
перетиніi-го рядка і j-го стовпця.
Відповідно до методу аналізу ієрархій для опису оцінок використовуються цілі числа від 1 до 9.
При цьому:
aij= 1 означає, що i-й і j-й критерії однаково важливі,
aij= 5 відображає думку, що i-й критерій значно важливіше, ніж j-й,
aij= 9 вказує, що i-й критерій надзвичайно важливіше j-го.
Слайд 20
3.Cпособи визначення
вагових коефіцієнтів
Теорія Прийняття рішень
© ЄА.
Лавров, 2014-2019
/14
Інші проміжні значення між 1 і 9
інтерпретуються аналогічно.
Узгодженість таких позначень забезпечується наступною умовою:
якщо aij = k, то автоматично aji = 1 / k. Крім того,
всі діагональні елементи aij матриці А
повинні бути рівні 1, так як вони виражають оцінку критеріїв щодо самих себе.
Слайд 21
3.Cпособи визначення
вагових коефіцієнтів Приклад.
Покажемо, як визначається матриця порівняння
А для задачі вибору Мартіна із 1-го прикладу лекції .
Головний
ієрархічний рівень(критерії академічної репутації університету та місцезнаходження)
З точки зору Мартіна, академічна репутація університету значно важливіше його місцезнаходження.
Отже, він приписує елементу (2, 1) матриці А значення 5, тобто a21 = 5.
Це автоматично передбачає, що a12 = 1/5.
Позначивши через R і L критерії репутації університету та його місцезнаходження, можна записати матрицю порівняння наступним чином.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 22
3.Cпособи визначення
вагових коефіцієнтів Приклад.
Відносні ваги критеріїв R і
L можуть бути визначені шляхом ділення елементів кожного стовпця на
суму елементів цього ж стовпця.Отже, для нормалізації матриці А ділимо елементи першого стовпця на величину 1 + 5 = 6,
елементи другого - на величину 1 + 1/5 = 1,2.
Шукані відносні ваги wR и wL критеріїв обчислюються тепер у вигляді середніх значень елементів відповідних рядків нормализованої матриці А. Отже,
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 23
3.Cпособи визначення
вагових коефіцієнтів Приклад.
Результат обчислень
wR = 0,83 та
wL = 0,17.
Стовпці матриці N однакові, що має місце лише у випадку, коли ОПР проявляє ідеальну узгодженість у визначенні елементів матриці А.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 24
3.Cпособи визначення
вагових коефіцієнтів
Теорія Прийняття рішень
© ЄА.
Лавров, 2014-2019
/14
Відносні ваги альтернативних рішень, відповідних університетам А, В і
С, обчислюються в межах кожного критерію R і L з використанням двох матриць порівняння.Елементи матриць АR і АL визначені на основі суджень Мартіна, що стосуються "ступеня реалізованості критерію" у кожному з 3 університетів.
Слайд 25
3.Cпособи визначення
вагових коефіцієнтів
Величини (wRA, wRB, wRC) = (0,545,
0,273, 0,182) дають ваги для університетів А, В і С
з точки зору академічної репутаціїАналогічно величини (wLA, wLB, wLC) = (0,129, 0,277, 0,594) є відносними вагами, що стосуються місцезнаходження університетів.
Величини (wRA, wRB, wRC) = (0,545, 0,273, 0,182) дають відповідні ваги для університетів А, В і С з точки зору академічної репутації. Аналогічно величини (wLA, wLB, wLC) = (0,129, 0,277, 0,594) є відносними вагами, що стосуються місцезнаходження університетів.
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
При діленні елементів кожного стовпця матриць АR і АL на суму елементів цих же стовпців отримуємо нормалізовані матриці.
Слайд 27
4.Узгодженість матриць порівнянь
.
Величини (wRA, wRB, wRC) = (0,545, 0,273,
0,182) дають відповідні ваги для університетів А, В і С
з точки зору академічної репутації. Аналогічно величини (wLA, wLB, wLC) = (0,129, 0,277, 0,594) є відносними вагами, що стосуються місцезнаходження університетів.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
У попередньому прикладі відзначали, що всі стовпці нормалізованих матриць N і NR ідентичні, а стовпці матриці NLтакими не є.
Однакові стовпці вказують на те, що результуючі відносні ваги зберігають одне і те ж значення незалежно від того, як виконується порівняння.
В цьому випадку говорять, що
вихідні матриці порівняння
А і АR, є узгодженими.
Отже, матриця АL не є такою.
Слайд 28
4.Узгодженість матриць порівнянь
Узгодженість означає, що рішення буде узгоджене з
визначенням парних порівнянь критеріїв або альтернатив.
З математичної точки зору
узгодженість матриці А означає, що aijajk = aik для всіх i, j та k
Наприклад, в матриці AR із прикладу(див. вище)
a13 = 3 та a12a23 = 3
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 29
4.Узгодженість матриць порівнянь
Величини (wRA, wRB, wRC) = (0,545, 0,273,
0,182) дають відповідні ваги для університетів А, В і С
з точки зору академічної репутації. Аналогічно величини (wLA, wLB, wLC) = (0,129, 0,277, 0,594) є відносними вагами, що стосуються місцезнаходження університетів.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Властивість узгодженості вимагає лінійної залежності стовпців (і рядків) матриці А.
Зокрема, стовпці будь-якої матриці порівнянь
розмірністю 2x2 є залежними
така матриця завжди є узгодженою.
Не всі матриці порівнянь є узгодженими.
Приймаючи до уваги, що такі матриці будуються на основі людських суджень,
можна очікувати деяку ступінь неузгодженості.
Слайд 30
4.Узгодженість матриць порівнянь
Теорія Прийняття рішень
© ЄА. Лавров,
2014-2019
/14
Щоб з'ясувати, чи є рівень узгодженості "допустимим", необхідно визначити відповідну
кількісну міру для матриці порівнянь А.У прикладі ми бачили, що ідеально узгоджена матриця А породжує нормализовану матрицю N, в якій всі стовпці однакові
Слайд 31
4.Узгодженість матриць порівнянь
Величини (wRA, wRB, wRC) = (0,545, 0,273,
0,182) дають відповідні ваги для університетів А, В і С
з точки зору академічної репутації. Аналогічно величини (wLA, wLB, wLC) = (0,129, 0,277, 0,594) є відносними вагами, що стосуються місцезнаходження університетів.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
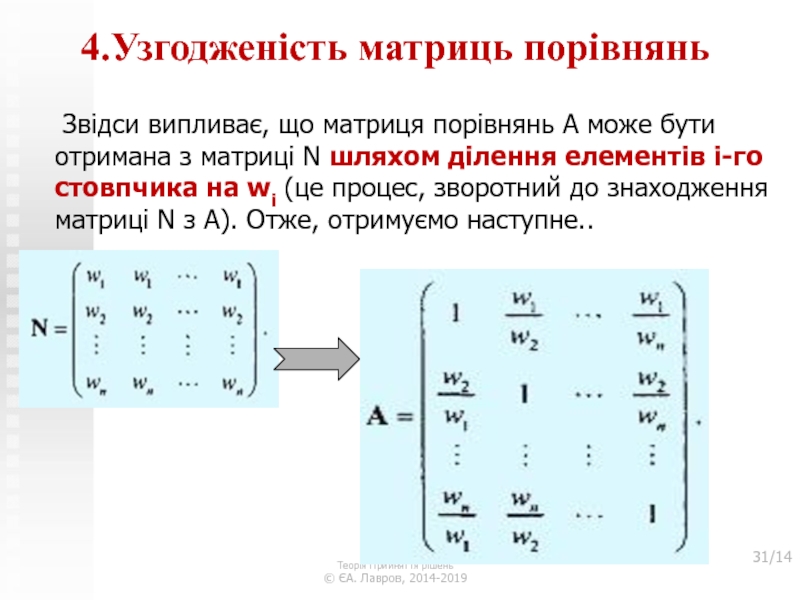
Звідси випливає, що матриця порівнянь А може бути отримана з матриці N шляхом ділення елементів i-го стовпчика на wi (це процес, зворотний до знаходження матриці N з А). Отже, отримуємо наступне..
Слайд 32
4.Узгодженість матриць порівнянь
Величини (wRA, wRB, wRC) = (0,545, 0,273,
0,182) дають відповідні ваги для університетів А, В і С
з точки зору академічної репутації. Аналогічно величини (wLA, wLB, wLC) = (0,129, 0,277, 0,594) є відносними вагами, що стосуються місцезнаходження університетів.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Використовуючи наведене визначення матриці А, маємо.
Слайд 33
4.Узгодженість матриць порівнянь
Величини (wRA, wRB, wRC) = (0,545, 0,273,
0,182) дають відповідні ваги для університетів А, В і С
з точки зору академічної репутації. Аналогічно величини (wLA, wLB, wLC) = (0,129, 0,277, 0,594) є відносними вагами, що стосуються місцезнаходження університетів.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
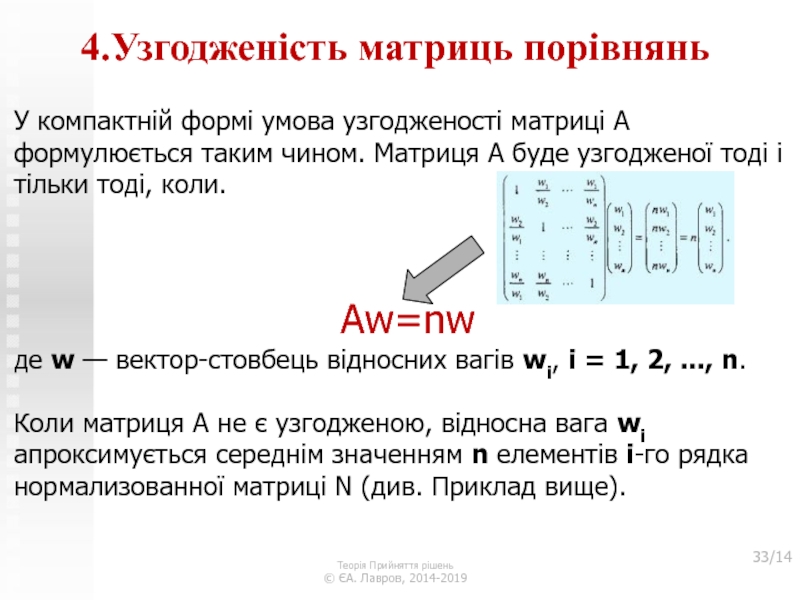
У компактній формі умова узгодженості матриці А формулюється таким чином. Матриця А буде узгодженої тоді і тільки тоді, коли.
Aw=nw
де w — вектор-стовбець відносних вагів wi, i = 1, 2, ..., n.
Коли матриця А не є узгодженою, відносна вага wi апроксимується середнім значенням n елементів i-го рядка нормализованної матриці N (див. Приклад вище).
Слайд 34
4.Узгодженість матриць порівнянь
Коли матриця А не є узгодженою, відносна
вага wi апроксимується середнім значенням n елементів i-го рядка нормализованої
матриці N (див. Приклад вище).не співпадають
Не узгоджена матр
Узгоджена матр
співпадають
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Слайд 35
4.Узгодженість матриць порівнянь
Позначивши через w обчислену оцінку (середнє значення),
можна показати, що
, де nmax ≥ nВ цьому випадку, чим ближче nmax до n,
тим більш узгодженою є
матриця порівняння А
Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
В
Слайд 36
4.Узгодженість матриць порівнянь
.
Величини (wRA, wRB, wRC) = (0,545, 0,273,
0,182) дають відповідні ваги для університетів А, В і С
з точки зору академічної репутації. Аналогічно величини (wLA, wLB, wLC) = (0,129, 0,277, 0,594) є відносними вагами, що стосуються місцезнаходження університетів.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
В результаті згідно з методом аналізу ієрархій обчислюється коефіцієнт узгодженості у вигляді
.
Де
- коефіцієнт узгодженості матриці А
-стохастичний коефіцієнт узгодженості
матриці А
Стохастичний коефіцієнт узгодженості RI визначається емпіричним шляхом
як середнє значення коефіцієнта CI для великої вибірки генерованих випадковим чином матриць порівняння А.
Слайд 37
4.Узгодженість матриць порівнянь
.
Величини (wRA, wRB, wRC) = (0,545, 0,273,
0,182) дають відповідні ваги для університетів А, В і С
з точки зору академічної репутації. Аналогічно величини (wLA, wLB, wLC) = (0,129, 0,277, 0,594) є відносними вагами, що стосуються місцезнаходження університетів.Теорія Прийняття рішень
© ЄА. Лавров, 2014-2019
/14
Коефіцієнт узгодженості CR використовується для перевірки узгодженості матриці порівняння А наступним чином.
Якщо CR <0,1,
рівень неузгодженості є прийнятним.
Інакше рівень неузгодженості
матриці порівняння А є високим,
ОПР , рекомендується перевірити елементи парного порівняння aij матриці А в цілях отримання більш узгодженої матриці.
Слайд 38
4.Узгодженість матриць порівнянь
.
Теорія Прийняття рішень
© ЄА. Лавров,
2014-2019
/14
Значення nmax обчислюється на основі
матричного рівняння При цьому неважко помітити, що i-e рівняння цієї системи має вигляд:Оскільки , легко перевірити, що
Величину nmax можна визначити шляхом обчислення вектор-стовпця Aw з наступним сумувуванням його елементів.
Слайд 39
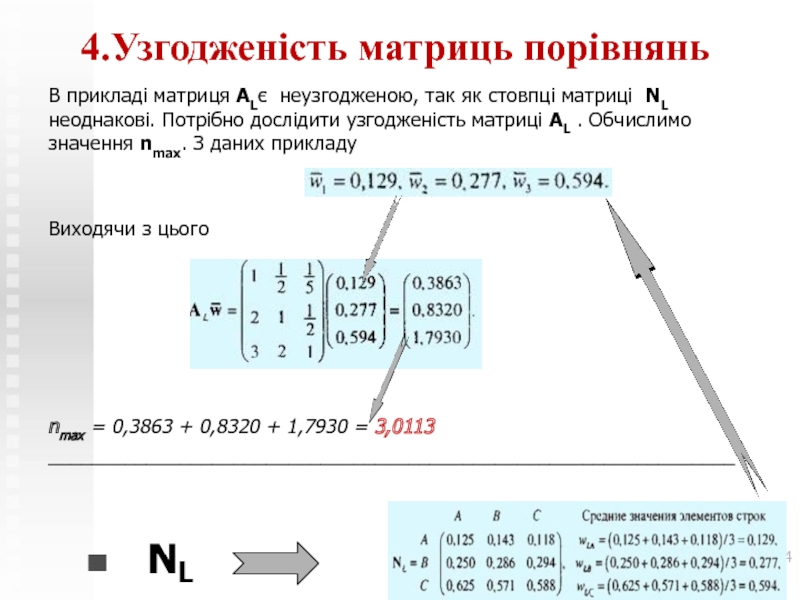
4.Узгодженість матриць порівнянь
В прикладі матриця ALє неузгодженою, так як
стовпці матриці NL неоднакові. Потрібно дослідити узгодженість матриці AL .
Обчислимо значення nmax. З даних прикладуВиходячи з цього
nmax = 0,3863 + 0,8320 + 1,7930 = 3,0113
_______________________________________________________________
/14
Слайд 40
4.Узгодженість матриць порівнянь
nmax = 0,3863 + 0,8320 + 1,7930
= 3,0113
Таким чином , для n = 3 маємо
Оскільки
CR < 0,1, рівень узгодженості матриці AL є припустимим
/14