центр проекций;
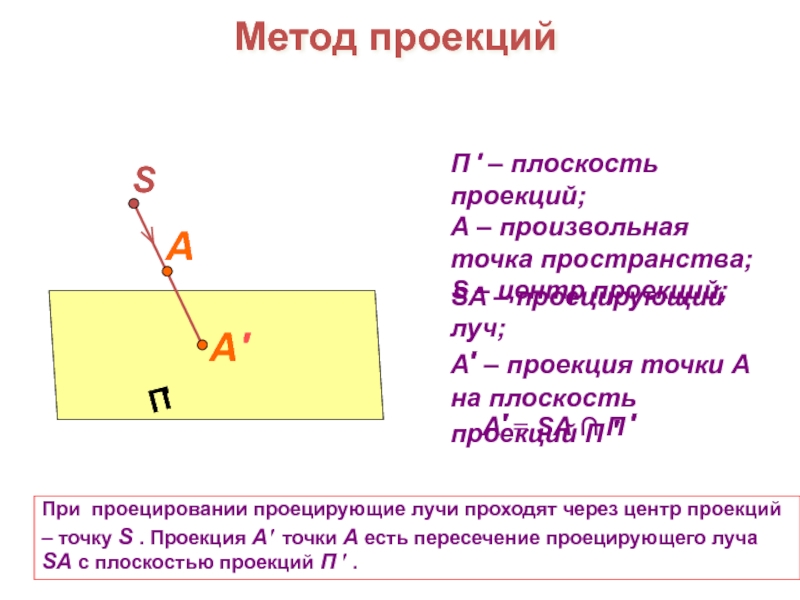
А′ = SA ∩ П ′
S
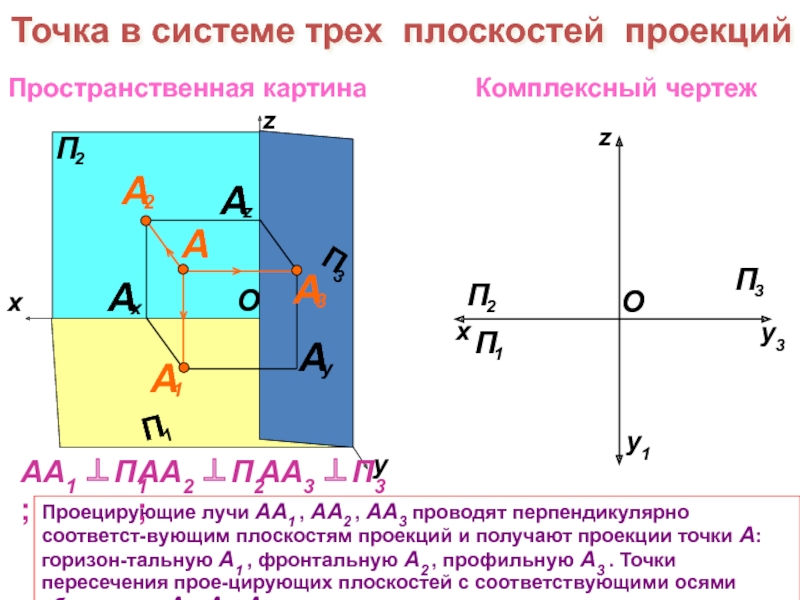
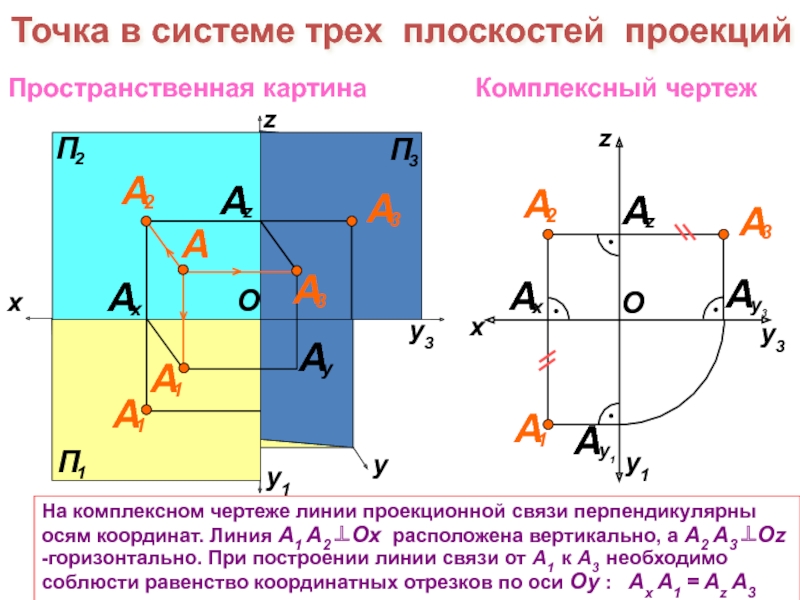
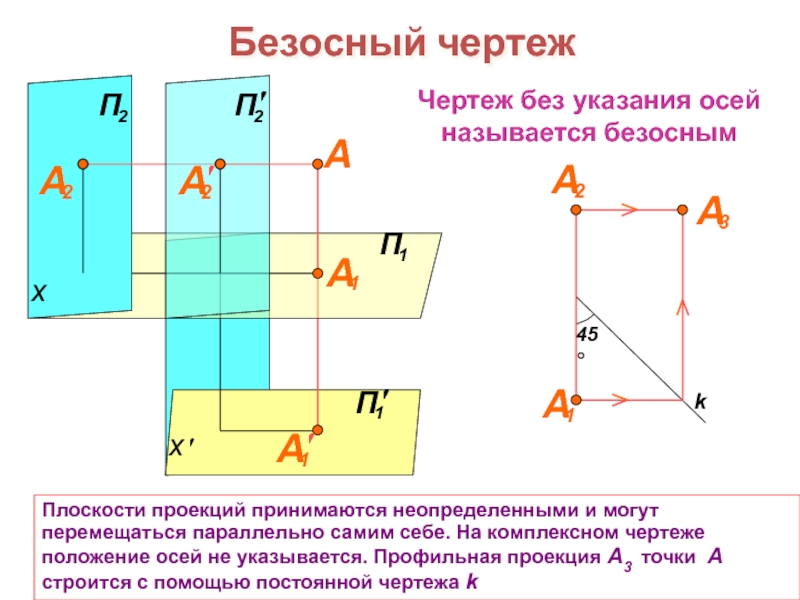
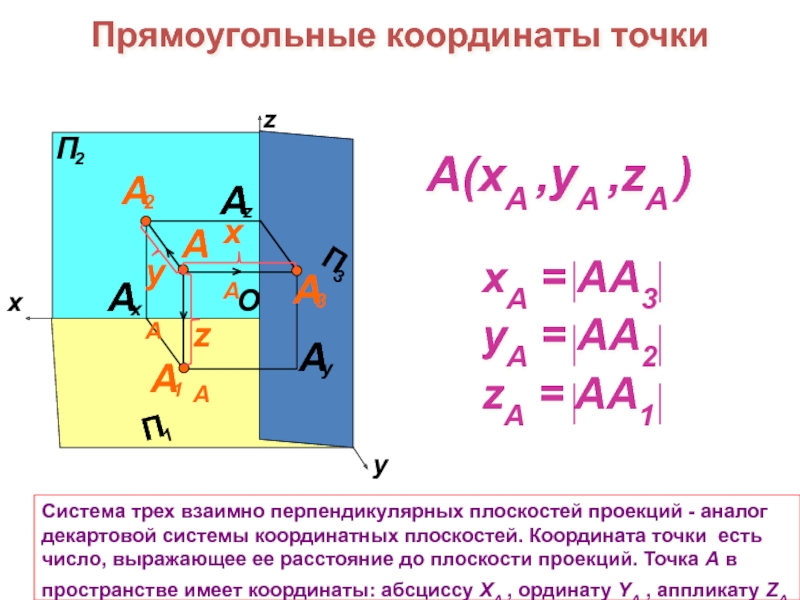
При проецировании проецирующие лучи
проходят через центр проекций – точку S . Проекция А′ точки А есть пересечение проецирующего луча SA с плоскостью проекций П ′ . Метод проекций
SA – проецирующий луч;
А′ – проекция точки А на плоскость проекций П ′