Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое программирование (математическая теория принятия оптимальных
Содержание
- 1. Математическое программирование (математическая теория принятия оптимальных
- 2. Примеры задач математического программирования Задача планирования производства
- 3. Общая задача линейного программированияЛинейная форма Система условий(система ограничений)Условия ограничений по знаку
- 4. Каноническая задача линейного программирования
- 5. Основные определенияДопустимое решение (план) – вектор
- 6. Теорема 1: Всякая задача линейного программирования может
- 7. Различные формы записи ЗЛПОбщая 2. Каноническая
- 8. Геометрические свойства З.Л.ПРассмотрим симметричную форму задания задачи
- 9. Геометрический способ решения задачи линейного программированияn=2
- 10. Геометрический способ решения n=2
- 11. Геометрический способ решения n = 2
- 12. Геометрический способ решения З.Л.П( в пространстве)n=3
- 13. Выпуклые множестваГеометрическое представление
- 14. Свойства З.Л.П1.Теорема 1. Множество планов З.Л.П –
- 15. Опорные планы З.Л.П.Определение: все угловые точки множества
- 16. Критерий опорности плана З.Л.ПТеорема 3 ( критерий
- 17. Пример G
- 18. Алгебраическая характеристика опорного планаZ(x)= 3х1+х2-2х3→max2x1 - x2
- 19. Базис опорного планаХо= (х1о;х2о;…хno) – опорный план.Если
- 20. Переход от одного опорного плана к другомуХО
- 21. Преобразование опорного планаПусть дана каноническая ЗЛП
- 22. Преобразование опорного планаПусть дан опорный план Хо
- 23. Преобразование опорного плана As1x1o+As2x2o+…+Asrxro
- 24. Что при этом произойдет с Z(X)? Подставим
- 25. Признак оптимальности планаТеорема Если для плана Хо
- 26. ОсновоположникиЛ.В.Канторович (1912-1986) академик РАН, Нобелевский лауреат- Российский математикДжорж Данциг(1914-2005) американский математик
- 27. Блок-схема алгоритма симплекс-метода1.Определение
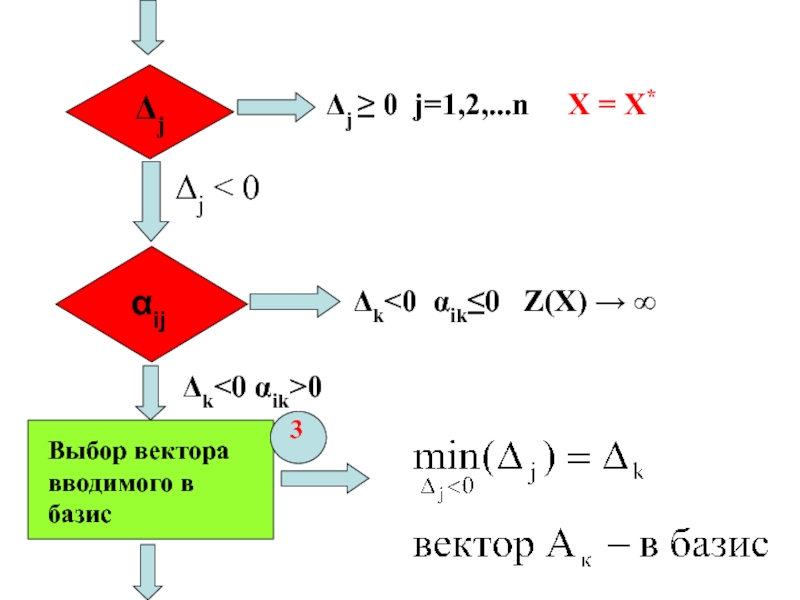
- 28. ΔjΔj ≥ 0 j=1,2,...n X = X* αijΔj < 0Δk
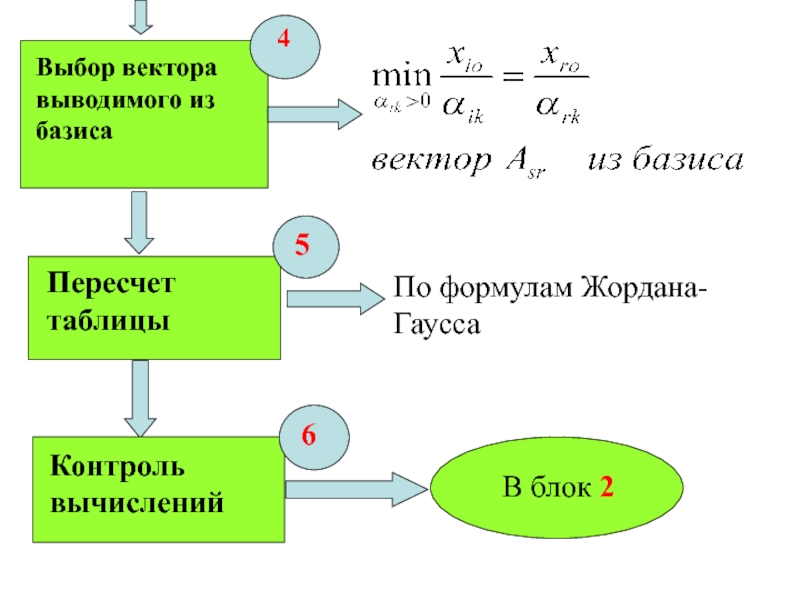
- 29. Выбор вектора выводимого из базиса 4Пересчет таблицыПо формулам Жордана-Гаусса5Контроль вычислений В блок 26
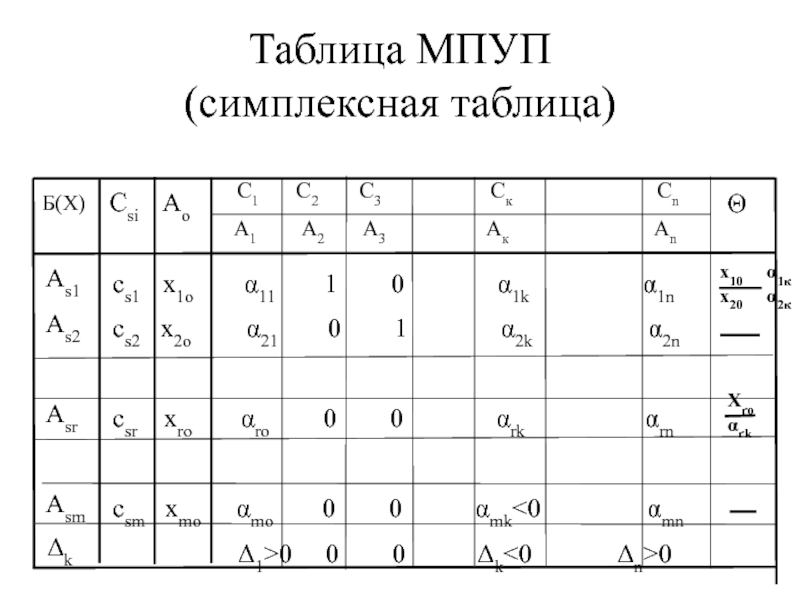
- 30. Таблица МПУП (симплексная таблица) С1
- 31. Определение первоначального опорного планаЕсли ЗЛП задана в
- 32. Определение первоначального опорного планаЕсли ЗЛП задана в
- 33. Теорема о решении вспомогательной задачиЕсли в оптимальном
- 34. ПРИМЕР Исходная
- 35. Двойственность в линейном программированииИсходная задача Хj
- 36. Свойства пары взаимно двойственных задач1.Z(x) ≤ Ž(y)
- 37. Теоремы двойственностиПервая теорема двойственности. Если одна из
- 38. Теоремы двойственностиВторая теорема двойственности: для того чтобы
- 39. Условия дополнительной нежёсткостиЕсли строчное условие i исходной
- 40. Условия дополнительной нежёсткостиЕсли столбцовое условие j исходной
- 41. Теоремы двойственностиРассмотрим пару двойственных задач
- 42. Теоремы двойственностиТеорема об оптимальных оценках(Третья теорема двойственности)Если
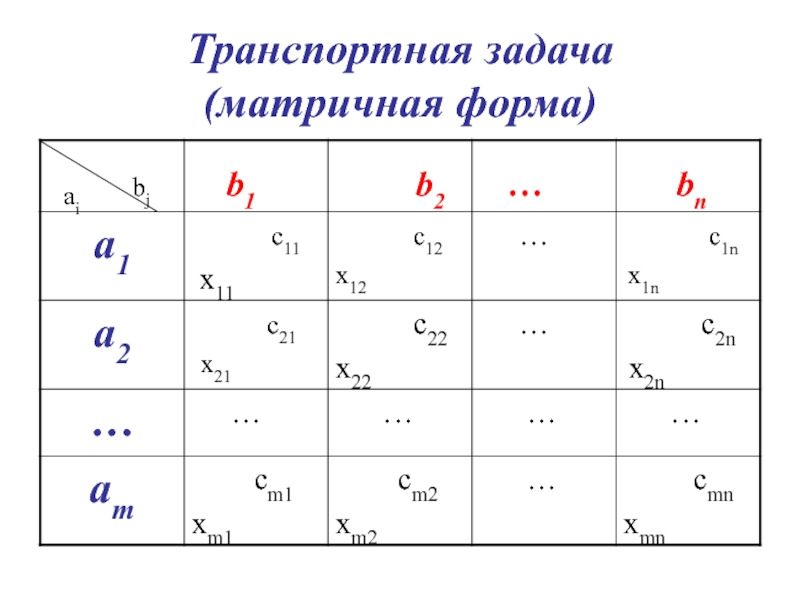
- 43. Транспортная задача (матричная форма)аi bj
- 44. Транспортная задача (сетевая форма)Дана транспортная сеть1921163215343311211597106813ПоставщикиПотребители
- 45. Математическая модель Т-задачи (матричная форма)Z(X) =
- 46. Свойства Т - задачиТеорема: Для того чтобы
- 47. Методы построения первоначального опорного плана Т-задачиМетод северо-западного угла.Метод минимального элемента.Метод Фогеля.
- 48. Метод северо-западного углааibj
- 49. Метод минимального элементааibj
- 50. Метод минимального элементаmin (aij) = a13 =
- 51. Цепочки и циклыЕсли в позиции (ij) имеется
- 52. Цепочки и циклыаibj
- 53. Теорема
- 54. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математическое программирование
(математическая теория принятия оптимальных решений)
Проф. Сагитов Р.В.
Слайд 2Примеры задач математического программирования
Задача планирования производства
(оптимальное использование
ресурсов)
2. Задача распределения работ.
3. Задача оптимального распределения финансовых ресурсов.
Слайд 3Общая задача линейного программирования
Линейная форма
Система условий
(система ограничений)
Условия ограничений
по знаку
Слайд 5Основные определения
Допустимое решение (план) – вектор
Х = (х1,
х2,…,хn) -удовлетворяющий системе ограничений ЗЛП.
Решение ЗЛП (оптимальный план) – вектор
Х* = (х1*, х2*,…,хn*) , доставляющий максимальное значение линейной формет.е. Z( Х* ) = max Z(X)
Слайд 6Теорема 1: Всякая задача линейного программирования может быть приведена к
каноническому виду.
1.1. Задача минимизации Z(x) →max равносильна задаче
- Z(x) →min 1.2. Неравенство равносильно уравнению и неравенству
1.3 Переменная, на которую не наложено условие неотрицательности, можно представить в виде хj= х1j – х2j ;
Слайд 7Различные формы записи ЗЛП
Общая 2. Каноническая .3.Симмет
ричная
Z(x) →extr Z(Х) →max Z(Х)→max
AX≤B AX=B AX≤B
AX≥B X≥0 X≥0
AX=B
Слайд 8Геометрические свойства З.Л.П
Рассмотрим симметричную форму задания задачи линейного программирования в
матричном виде
Z(х) →maxАХ ≤ В
X ≥0
Пусть переменных n=2 .
G
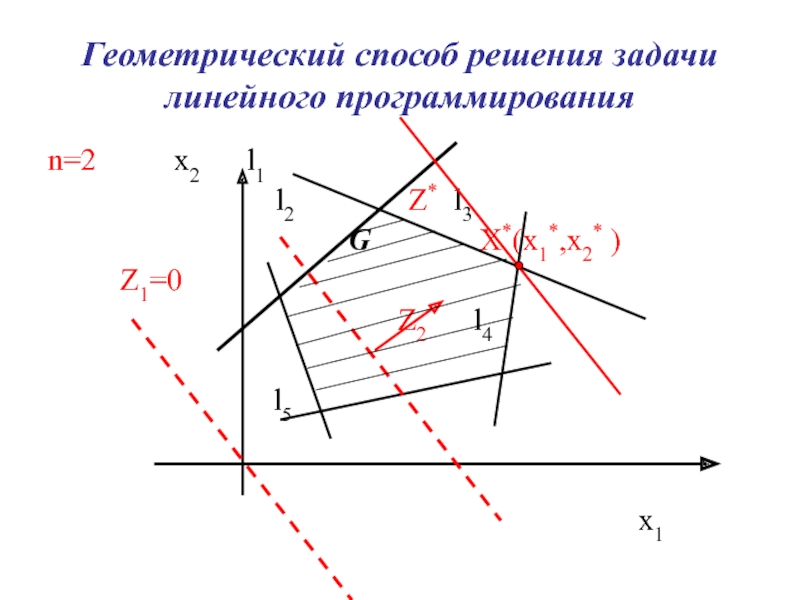
Слайд 9Геометрический способ решения задачи линейного программирования
n=2
x2 l1
l2 Z* l3G X*(x1*,x2* )
Z1=0
Z2 l4
l5
x1
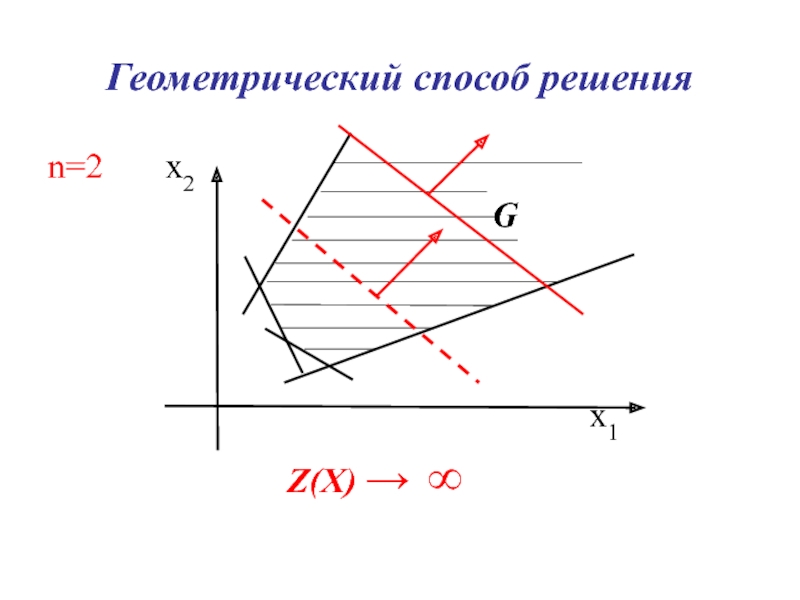
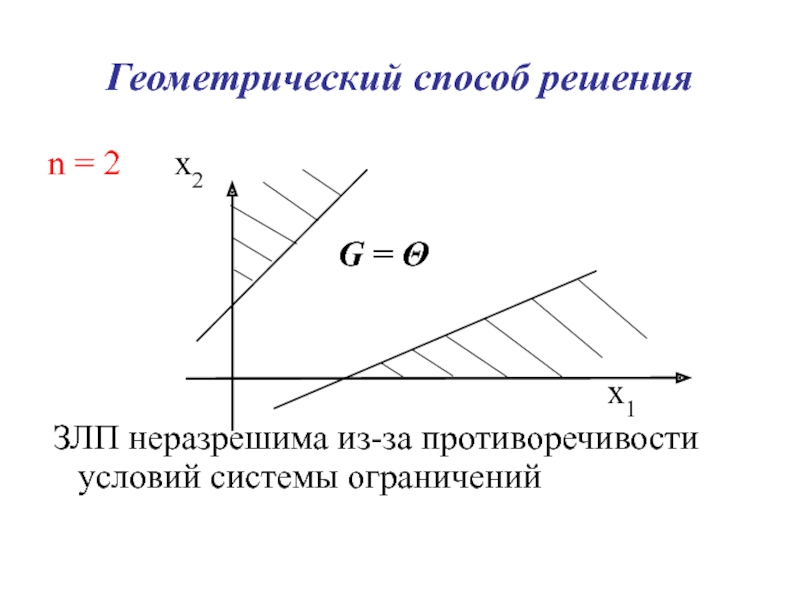
Слайд 11Геометрический способ решения
n = 2 x2
G = Θ
x1
ЗЛП неразрешима из-за противоречивости условий системы ограничений
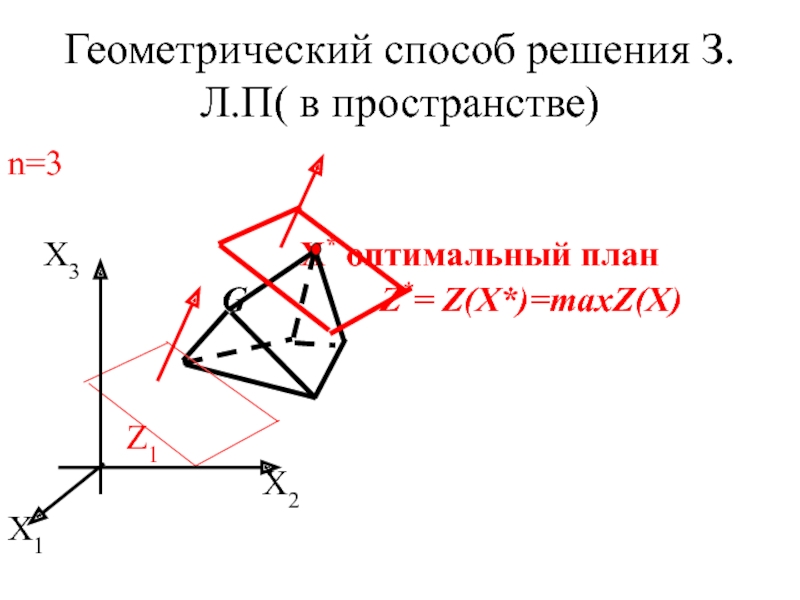
Слайд 12Геометрический способ решения З.Л.П( в пространстве)
n=3
X3
X* оптимальный план
G Z*= Z(Х*)=maxZ(X)
Z1
X2
X1
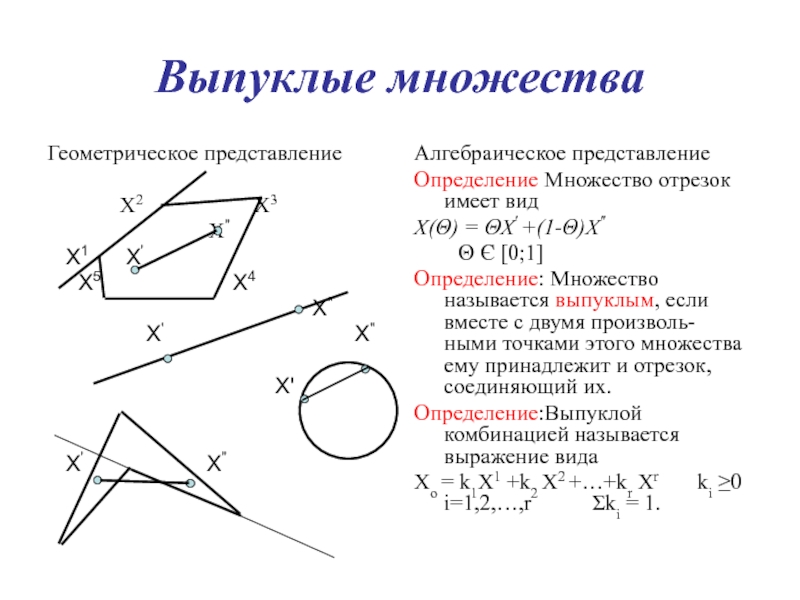
Слайд 13Выпуклые множества
Геометрическое представление
Х2
Х3
Х"
Х1 Х'
Х5 Х4
Х"
Х' Х"
Х'
Х' Х"
Алгебраическое представление
Определение Множество отрезок имеет вид
Х(Θ) = ΘХ' +(1-Θ)Х"
Θ Є [0;1]
Определение: Множество называется выпуклым, если вместе с двумя произволь- ными точками этого множества ему принадлежит и отрезок, соединяющий их.
Определение:Выпуклой комбинацией называется выражение вида
Хо = k1Х1 +k2 Х2 +…+kr Хr ki ≥0 i=1,2,…,r Σki = 1.
Слайд 14Свойства З.Л.П
1.Теорема 1. Множество планов З.Л.П – выпуклое множество.
2. Лемма.
Всякая точка выпуклого множества может быть представлена в виде выпуклой
комбинации угловых точек множества.3. Теорема 2. Решение З.Л.П. достигается в угловой точке множества планов З.Л.П.
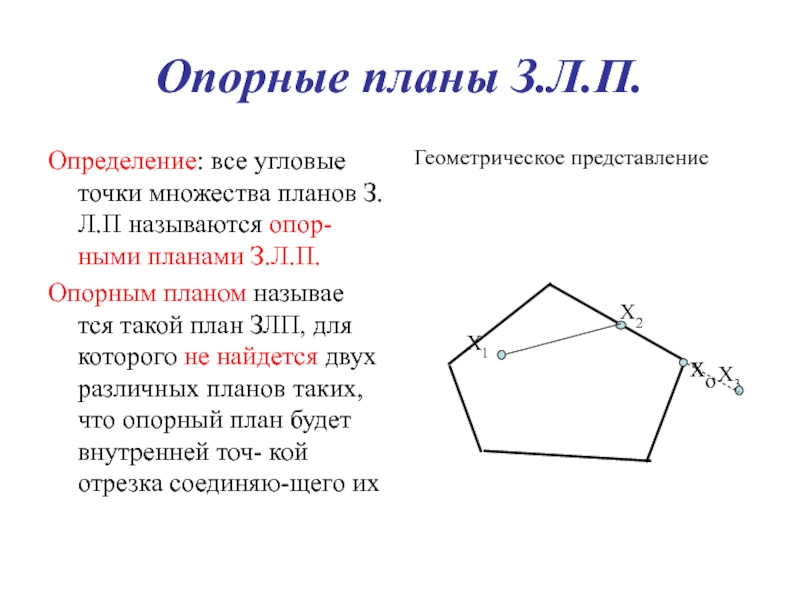
Слайд 15Опорные планы З.Л.П.
Определение: все угловые точки множества планов З.Л.П называются
опор-ными планами З.Л.П.
Опорным планом называе тся такой план ЗЛП, для
которого не найдется двух различных планов таких, что опорный план будет внутренней точ- кой отрезка соединяю-щего ихГеометрическое представление
Х2
Х1
Х3
xo
Слайд 16Критерий опорности плана З.Л.П
Теорема 3 ( критерий опорности плана ЗЛП)
Для
того чтобы план ЗЛП был опорным, необходимо и достаточно, чтобы
векторы условий, отвечающие положительным компонентам плана были линейно независимыми.Слайд 18Алгебраическая характеристика опорного плана
Z(x)= 3х1+х2-2х3→max
2x1 - x2 + x3 =
1
x1+2x2 – x3 = 3
xj ≥ 0
j=1,2,3Z(x)= 3х1+х2-2х3→max
x2 - (3/5)x3 = 1
x1 +(1/5)x3 = 1
xj ≥ 0 j=1,2,3
Xo = (1,1,0) Бхо (А1,А2)
Z(Xo) = 4.
Слайд 19Базис опорного плана
Хо= (х1о;х2о;…хno) – опорный план.
Если хј > 0,
то Ај = Аѕі , если хј = 0,
то Ај ≠ АѕіОпределение: Векторы, отвечающие положительным компонентам плана образуют базис опорного плана
Х1=(1,0,0,1) – базис Бх1 = {А1=Аѕ1;А4 =Аѕ2 } таким образом Бх1 ={Аѕ1 Аѕ2}.
Х2=(0,5,0,0) – вектор А2 = Аѕ1 войдет в базис, но его требуется дополнить еще каким либо вектором Бх2 = {А2 = Аѕ1 ; А? = Аѕ2}
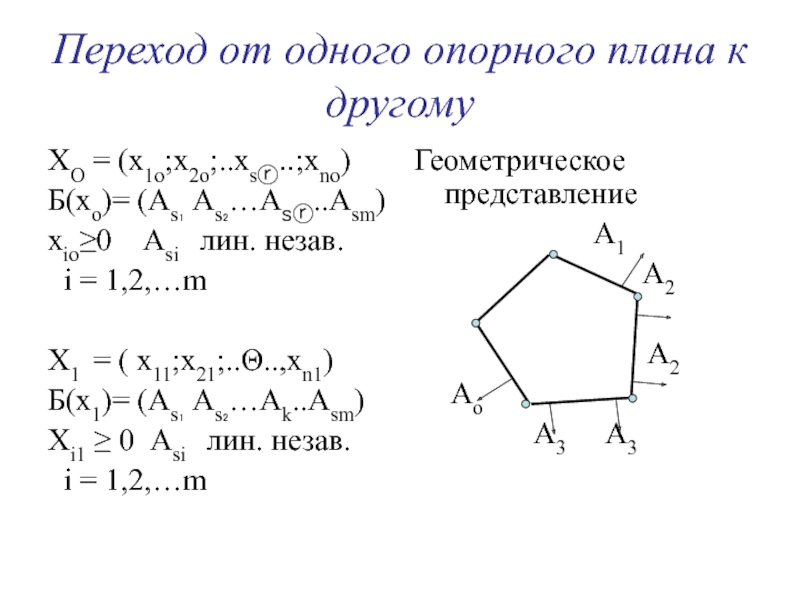
Слайд 20Переход от одного опорного плана к другому
ХО = (х1о;х2о;..xsⓡ..;хno)
Б(хо)= (Аѕ₁
Аѕ₂…Аѕⓡ..Аѕm)
хiо≥0 Аѕi лин. незав.
i = 1,2,…m
Х1 =
( х11;х21;..Θ..,хn1)Б(х1)= (Аѕ₁ Аѕ₂…Аk..Аѕm)
Хi1 ≥ 0 Аѕi лин. незав.
i = 1,2,…m
Геометрическое представление
А1
А2
А2
Ао
А3 А3
Слайд 21Преобразование опорного плана
Пусть дана каноническая ЗЛП
Z(Х) = Σсj
хj → maxA1x1 +A2x2 +…+ Amxm +…+ Anxn = B
G хj ≥ 0 j = 1,2,…,n
А1 ,А2 ,…,Аm ,…,Аn – векторы условий
В – вектор ограничений
Слайд 22Преобразование опорного плана
Пусть дан опорный план Хо =(х1ох2о... х®о..хmо 0…0)
Базис
плана Б(Хо)={Аs1;Аs2;…;Аsr;…;Аsm }
{ X(Θ) = (Xo - Θαk) ; Θ } Є Gαk =(α1k; α2k;… αrk;…αmk )
Аs1 α1k +Аs2 α2k+…+Аsrαrk+…Аsmαmk = Ak
Аs1 х1о +Аs2 х2о+…+Аsrхsr+…+Аsmхmo +Am+1 0+…+An0 =В
Аs1 α1k +Аs2 α2k+…+Аsrαrk+…+Аsmαmk – Ak = 0
Слайд 23Преобразование опорного плана
As1x1o+As2x2o+…+Asrxro …+A smxmo +
ΣAj0 = B
(As1α1k+As2α2k+…+Asrαrk …+A smαmk -
Ak = 0)Θ Аs1(x1o-Θα1k)+ …+ Asr(xro-Θαrk)+…+AkΘ = B
(xio- Θαik) ≥ 0 i=1,2,…,m и Θ≥0
Θ≤ выберем Θо = min =
αik>0
(1)
(2)
Слайд 24Что при этом произойдет с Z(X)?
Подставим новый план
{ X(Θo) = (Xo - Θoαk) ; Θo
} Є G в Z(X) !Z(X(Θ)) = Σcj(xj(Θo )) =
Z(X(Θo))= Z(Xo) – ΘΔk , где Δk =
Слайд 25Признак оптимальности плана
Теорема Если для плана Хо выполняется условие Δj
≥ 0 при j = 1,2,…,n ,то план Хо= Х*
т.е. оптимальный план.Следствие Если существует Δк < 0 и при этом все αik≤ 0 , то ЗЛП не имеет решения из-за неограниченности линейной формы на множестве планов.
(Z(X) → ∞)
Слайд 26Основоположники
Л.В.Канторович (1912-1986) академик РАН, Нобелевский лауреат- Российский математик
Джорж Данциг(1914-2005) американский
математик
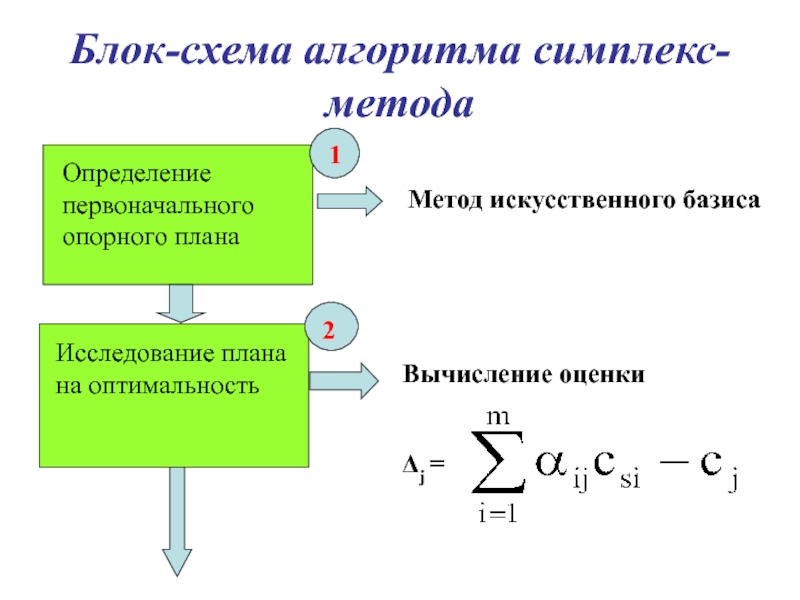
Слайд 27Блок-схема алгоритма симплекс-метода
1.
Определение первоначального опорного плана
Метод искусственного базиса
Исследование плана на оптимальность
Вычисление оценки
Δj =
1
2
Слайд 29Выбор вектора выводимого из базиса
4
Пересчет таблицы
По формулам
Жордана-Гаусса
5
Контроль вычислений
В блок 2
6
Слайд 30Таблица МПУП
(симплексная таблица)
С1 С2
C3
Ск СnА1 А2 A3 Ак Аn
Б(Х)
Csi
Ao
Θ
As1
As2
Asr
Asm
Δk
cs1 x1o α11 1 0 α1k α1n
cs2 x2o α21 0 1 α2k α2n
csr xro αro 0 0 αrk αrn
csm xmo αmo 0 0 αmk<0 αmn
Δ1>0 0 0 Δk<0 Δn>0
х10 α1к х20 α2к
Xro
αrk
Слайд 31Определение первоначального опорного плана
Если ЗЛП задана в симметричном виде
Z(х) →max
АХ ≤ В
X ≥0
Если все компоненты вектора В положи-телны, тогда в каждое уравнение вводится дополнительная переменная и первоначальный план очевиден.
Слайд 32Определение первоначального опорного плана
Если ЗЛП задана в каноническом виде
Z(х) →max
АХ = В
X ≥0
Тогда рассматривают вспомогательную задачу с искусственным базисом, который получается путем введения в каждое уравнение искусственной переменной.
Слайд 33Теорема о решении вспомогательной задачи
Если в оптимальном плане вспомогательной задачи
не содержатся искусственные переменные ,то полученный оптимальный план является первоначальным
опорным планом исходной задачи.Если оптимальное решение вспомогательной задачи содержит искусственную переменную, то исходная задача неразрешима из за противоречивости множества планов исходной задачи.
Слайд 34ПРИМЕР
Исходная
Вспомогательная
Z(X) = 3x1+x2
+2x3 →max Z(X)= -x4 – x7→maxx1 + x2 + x3 = 3 x1 + x2 + x3 + x4 = 3
Gиз x1 + x2 ≤ 1 x1 + x2 + x5 =1
x1 – x2 + x3 ≥ 1 Gвз x1 – x2 + x3 – x6 + x7 = 1
xj ≥ 0 j=1,2,3 xj ≥ 0 j=1,2,3,…,7
Xo = (0,0,0,3,1,0,1)
Слайд 35Двойственность в линейном программировании
Исходная задача
Хj ≥ 0
j = 1,2,…,n1
Двойственная задача
yi ≥ 0 i
= 1,2,…,m1yi не ограничены по знаку
i = m1 +1,m1 +2,…,m
Слайд 36Свойства пары взаимно двойственных задач
1.Z(x) ≤ Ž(y) для любых X
Є Gи.з. и У Є Gд.з.
2.Если для Xо Є Gи.з.
и Уо Є Gд.з Z(xо) = Ž(yо), то Хо = Х*, а Уо = У*.3.Если Ž(y) → -∞, то Gи.з = О
Замечание: В обратную сторону свойство 3 не всегда выполняется
Слайд 37Теоремы двойственности
Первая теорема двойственности.
Если одна из пары двойственных задач
разрешима, то разрешима и двойственная к ней, при этом Z(Х*)
= Ž(У*) .Если одна из пары двойственных задач не имеет решения, то неразрешима и двойственная к ней.
Слайд 38Теоремы двойственности
Вторая теорема двойственности: для того чтобы планы задач ХЄGиз
и УЄGдз были оптимальными планами соответствующих задач, необходимо и достаточно,
чтобы выполнялись следующие равенства:х*j ( ;
y*i( .
Слайд 39Условия дополнительной нежёсткости
Если строчное условие i исходной задачи выполняется как
неравенство Σаijx*j< bi , то переменная у*i = 0.
Если строчное
условие i исходной задачи выполняется как равенство Σаijx*j= bi , то переменная у*i > 0.Слайд 40Условия дополнительной нежёсткости
Если столбцовое условие j исходной задачи выполняется как
неравенство хj>0, то условие j двойственной выполняется как равенство Σаij
у*i= сjЕсли столбцовое условие j исходной задачи выполняется как равенство хj=0, то условие j двойственной выполняется как неравенство Σаij у*I > сj
Слайд 41Теоремы двойственности
Рассмотрим пару двойственных задач
yi ≥ 0 i = 1,2,…,m
Хj ≥ 0 j = 1,2,…,n
Введем функцию М(В) = max{Z(X)}
XЄG BЄB
из
Слайд 42Теоремы двойственности
Теорема об оптимальных оценках
(Третья теорема двойственности)
Если невырожденная задача линейного
программирования разрешима,
∂М(В)
/ ∂bi = yi* Замечание: ΔВ велико, то теорема не имеет применения – область устойчивости оценок А-1ΔВ ≥ 0
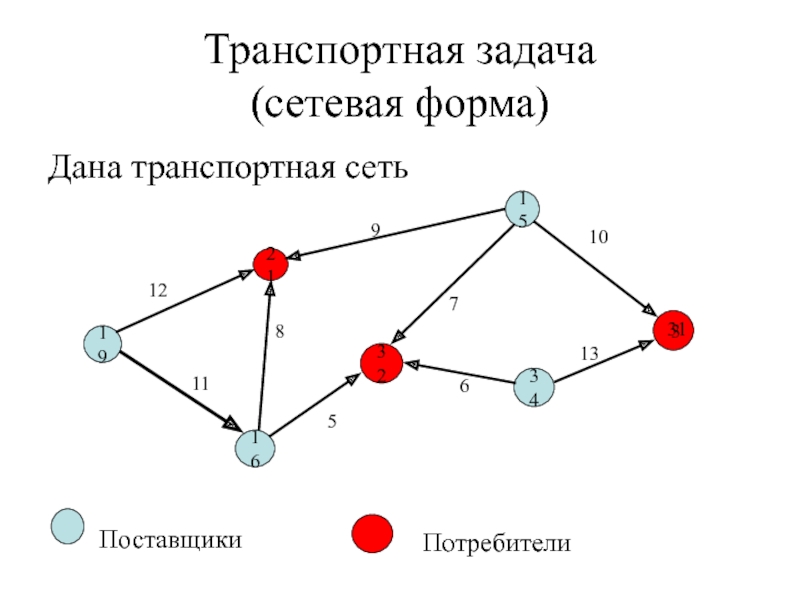
Слайд 44Транспортная задача
(сетевая форма)
Дана транспортная сеть
19
21
16
32
15
34
3
31
12
11
5
9
7
10
6
8
13
Поставщики
Потребители
Слайд 46Свойства Т - задачи
Теорема: Для того чтобы Т-задача была разрешима
необходимо о достаточно, чтобы выполнялось условие баланса
Σ аі = Σ bjТеорема: Ранг системы условий (ограничений ) Т – задачи равен m+n-1
i
j
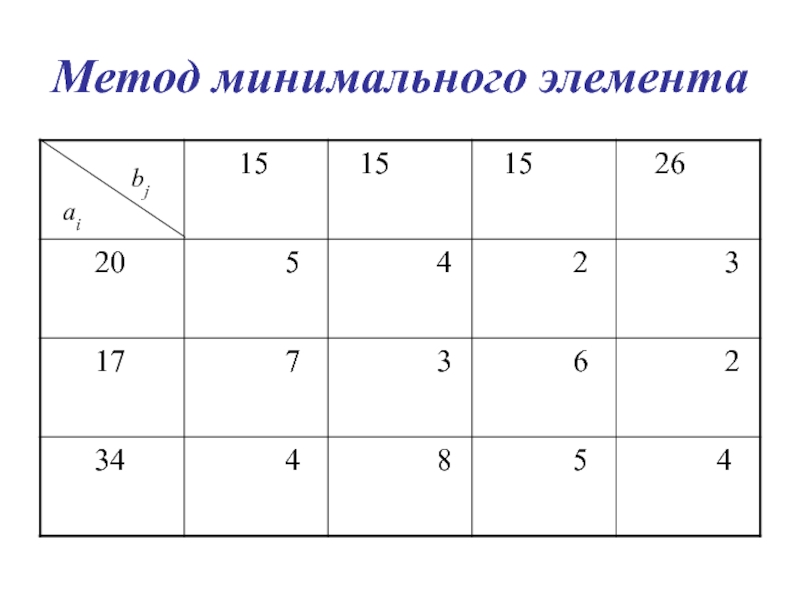
Слайд 47Методы построения первоначального опорного плана Т-задачи
Метод северо-западного угла.
Метод минимального элемента.
Метод
Фогеля.
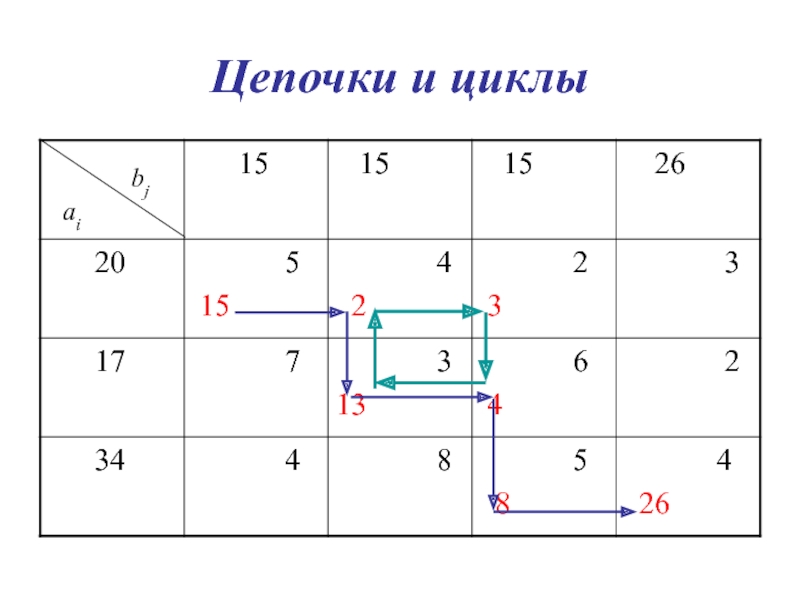
Слайд 51Цепочки и циклы
Если в позиции (ij) имеется перевозка хij >
0, то позиция называется отмеченной.
Последовательность отмеченных позиций, в которой из
каждой строки и каждого столбца последовательно включены две и только две отмеченные позиции называется цепочкойЦепочка, в которой первая позиция совпадает с последней называется циклом