Слайд 1Методы анализа сложных электрических цепей постоянного тока: применение законов Кирхгофа,
метод контурных токов. Уравнение баланса электрической мощности.
В электротехнике часто находят
применение сложные электрические цепи с несколькими активными или пассивными элементами. Если такая цепь содержит много узлов и контуров, то расчет цепи на основе первого и второго законов Кирхгофа будет связан с решением большого количества уравнений.
Метод токов ветвей (МТВ) основан на законах Кирхгофа. Число уравнений по МТВ равно количеству неизвестных токов ветвей и определяется как:
Количество уравнений, составляемых по I закону Кирхгофа, равно:
Количество уравнений, составляемых по II закону Кирхгофа, равно:
При составлении уравнений по II закону Кирхгофа следует выбирать независимые контуры, не содержащие источников тока.
Метод контурных токов (МКТ) позволяет уменьшить количество уравнений до числа:
Вводя понятие контурных токов, можно снизить порядок системы уравнений. Под контурными токами понимают условные (расчетные) токи, замыкающиеся в соответствующих контурах, направления и величины которых остаются неизменными. Зная значения контурных токов, можно легко найти токи во всех ветвях схемы.

Слайд 2
При расчете электрических цепей с применением законов Кирхгофа необходимо:
1. Выбрать
положительное направление токов во всех ветвях схемы;
2. Выбрать положительное направление
обхода контура;
3. Составить уравнения по законам Кирхгофа;
по первому закону Кирхгофа составить nу-1 уравнение, по второму закону Кирхгофа составить nв –nу +1. Общее число уравнений равно числу ветвей в схеме;
4. Полученную систему уравнений решают относительно неизвестных токов.
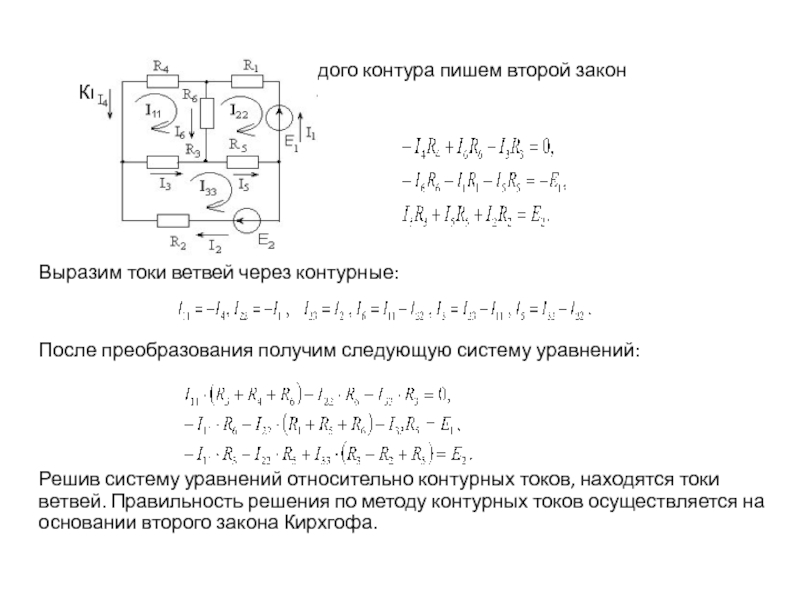
Составим систему уравнений для нахождения токов ветвей для схемы, изображенной на рисунке: Данная схема имеет четыре узла и шесть ветвей. Система уравнений по законам Кирхгофа имеет следующий вид:
Слайд 3
Имеем систему из шести уравнений с шестью неизвестными. Выразив токи
I1, I2, I5 через I4, I6,I3, получим:
Решая данную систему уравнений,
можно найти токи ветвей.
Число совместно решаемых уравнений равно числу ветвей схемы (числу неизвестных токов ветвей), поэтому его применение не всегда целесообразно.
В качестве переменных в методе контурных токов принимаются контурные токи.
В схеме выделяют независимые контуры. В каждом контуре произвольно выбирают направление контурных токов. За контурные токи удобно принять токи внешних ветвей схемы, которые входят только в данный контур.
Уравнения составляются на основе второго закона Кирхгофа, выражая токи ветвей через контурные токи.
Слайд 4
Для каждого контура пишем второй закон Кирхгофа:
Выразим токи ветвей
через контурные:
После преобразования получим следующую систему уравнений:
Решив систему уравнений относительно
контурных токов, находятся токи ветвей. Правильность решения по методу контурных токов осуществляется на основании второго закона Кирхгофа.
Слайд 5Баланс мощностей – это интерпретация закона сохранения энергии в
электротехнике. Мощность генераторов энергии в электрической цепи равна мощности потребителей:
причем
Где – мощность источников ЭДС;
– мощность источников тока;
– токи источников тока;
– напряжения на зажимах источников тока.
Эти суммы алгебраические. Источник может как вырабатывать, так и потреблять электрическую энергию (заряд аккумулятора). Если направления ЭДС и тока через источник ЭДС совпадают, мощность источника записывают в уравнении баланса мощностей с положительным знаком. Он работает в режиме генератора. При противоположных направлениях ЭДС и тока мощность в уравнении баланса учитывают с отрицательным знаком (режим потребителя).
Уравнение баланса электрической мощности.
Слайд 6
Определение знака мощности источника тока поясняет, на котором показана разметка
зажимов источника тока, вырабатывающего (а) или потребляющего (б) электрическую энергию.
Ток и напряжение U направлены в сторону уменьшения потенциала, что и позволяет разметить зажимы источника. Мощность потребителей (нагрузок)
Эта сумма арифметическая.
Погрешность расчета не должна превышать (1–3) %.
В некоторых случаях для упрощения расчетов токов рационально заменить источники тока эквивалентными источниками ЭДС или сделать обратное преобразование.
Слайд 7Метод узловых потенциалов. Метод двух узлов. Метод эквивалентного генератора, Метод
наложения (суперпозиции).
Метод узловых потенциалов является наиболее общим и широко
применяется для анализа цепей любой конфигурации. При расчете электрических цепей методом узловых потенциалов потенциал одного из узлов принимается равным нулю. Для всех остальных узлов составляют уравнения по первому закону Кирхгофа. Решив систему уравнений, определяют потенциалы узлов. Затем по закону Ома определяют токи ветвей. Для приведенной схемы электрической цепи, составим уравнения по методу узловых потенциалов. Примем потенциал узла d равным нулю, т.е. запишем первый закон Кирхгофа для узлов а,в,с.
Выразим токи по закону Ома через потенциалы узлов
Слайд 8
Подставим эти выражение в уравнения по первому закону Кирхгофа и
приведя подобные члены получим следующее уравнение:
где:
Решение системы уравнений позволяет определить
потенциалы узлов. Проверку правильности решения осуществляется на основании первого закона Кирхгофа.
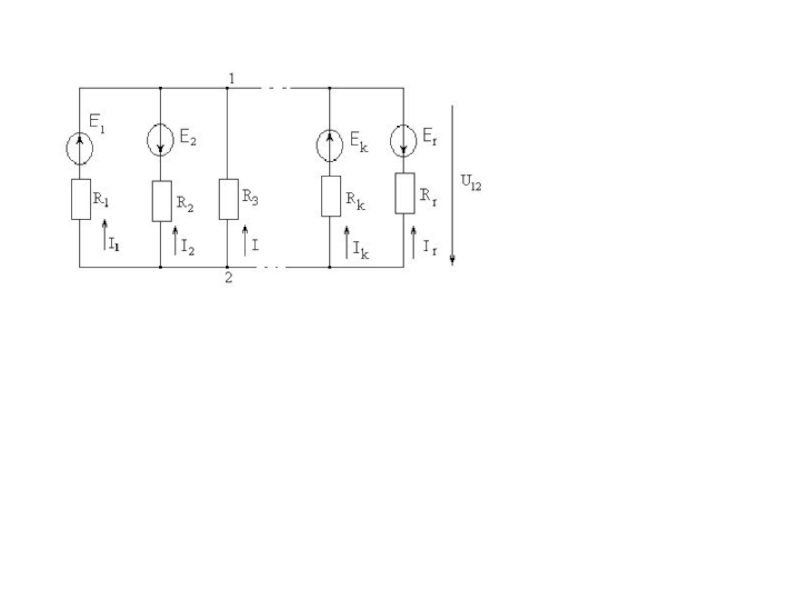
Метод двух узлов. Очень часто встречаются схемы с двумя узлами и произвольным числом ветвей, тогда требуется найти напряжение между двумя узлами. Рассмотрим схему содержащую два узла и произвольное число ветвей.
Слайд 10Метод эквивалентного генератора.
Данный метод основан на теореме об активном
двухполюснике. Применение данного метода целесообразно для определения тока в какой-либо
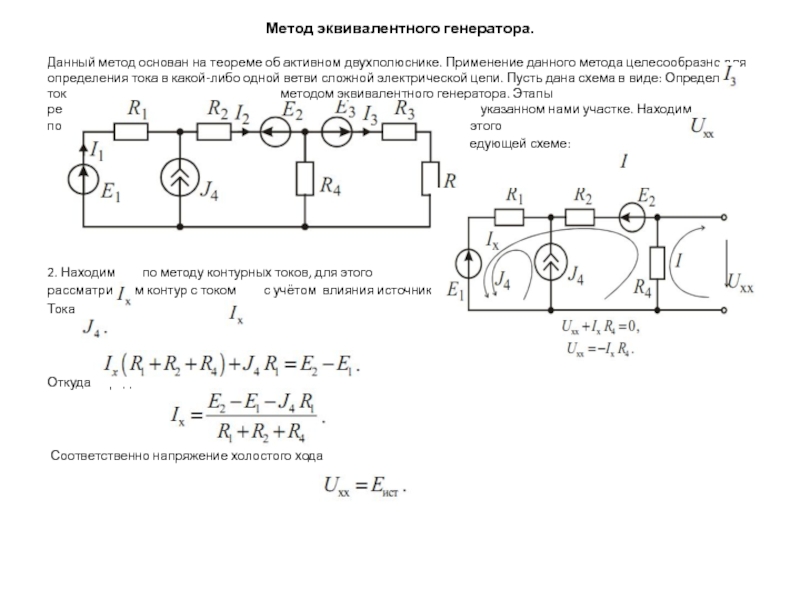
одной ветви сложной электрической цепи. Пусть дана схема в виде: Определим ток методом эквивалентного генератора. Этапы решения задачи. 1. Разрываем цепь в указанном нами участке. Находим по второму закону Кирхгофа, для этого
рассматриваем контур в следующей схеме:
2. Находим по методу контурных токов, для этого
рассматриваем контур с током с учётом влияния источника
Тока
Откуда определяем
Соответственно напряжение холостого хода
Слайд 11
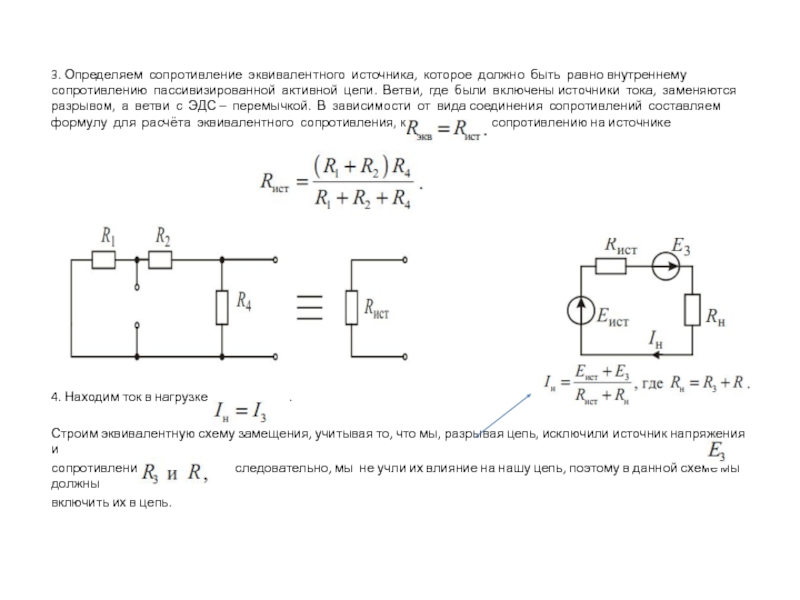
3. Определяем сопротивление эквивалентного источника, которое должно быть равно внутреннему
сопротивлению пассивизированной активной цепи. Ветви, где были включены источники тока,
заменяются разрывом, а ветви с ЭДС – перемычкой. В зависимости от вида соединения сопротивлений составляем формулу для расчёта эквивалентного сопротивления, которое равно сопротивлению на источнике
4. Находим ток в нагрузке .
Строим эквивалентную схему замещения, учитывая то, что мы, разрывая цепь, исключили источник напряжения и
сопротивления следовательно, мы не учли их влияние на нашу цепь, поэтому в данной схеме мы должны
включить их в цепь.
Слайд 12Метод наложения (суперпозиции).
Метод наложения основан на принципе независимости действия
источников энергии. Ток в любой ветви схемы равен алгебраической сумме
токов, возникающих в этой ветви под действием каждого отдельно работающего источника. Схему делят на столько подсхем, сколько источников энергии. В каждой подсхеме оставляют только один источник, остальные источники ЭДС закорачивают, источники тока – разрывают. Приемники во всех подсхемах остаются неизменными. Токи в подсхемах ищут методом эквивалентных преобразований. Токи в схеме вычисляют алгебраическим суммированием токов в подсхемах. Метод наложения рационально применять, если в схеме не больше трех источников энергии.
Рассмотрим применение метода на конкретном примере. Пример. Вычислить токи в схеме рис. 4.2, если известны значения ЭДС источников и сопротивления всех резисторов. Решение :
1. Выявим узлы (1, 2), ветви, направим токи.
2. Разобьем схему на две подсхемы (рис. 4.3, а, б).
3. Выявим узлы и ветви в первой подсхеме.
Ток появляется в источнике ЭДС, затем в узле 1 разветвляется на токи
Направления токов нужно указывать правильно. В подсхеме нет ветвей, содержащих больше одного резистора, т. е. нет последовательных соединений. Резисторы с сопротивлениями соединены параллельно. Их можно заменить одним резистором с эквивалентным сопротивлением

Слайд 13
После этого преобразования схема превращается в последовательное соединение с
В свернутой схеме ток , который вычислим по закону Ома:
Ток найдем по формуле разброса:
Ток можно определить с помощью первого закона Кирхгофа:
4. Выявим узлы и ветви во второй подсхеме, правильно направим токи. Эквивалентное сопротивление второй подсхемы
В свернутой схеме ток , который найдем по закону Ома:
Ток вычислим для разнообразия с помощью уравнения по второму закону Кирхгофа:
Отсюда
Ток определим посредством первого закона Кирхгофа:
5. Определим токи в исходной схеме алгебраическим суммированием токов в подсхемах (наложением подсхем):