Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы оптимальных решений
Содержание
- 1. Методы оптимальных решений
- 2. Оптимизация. Постановка задачиЛинейное программирование как научно-практическая дисциплина.
- 3. Линейное программированиеНаиболее часто используются оптимизационные модели принятиярешений.
- 4. Линейное программирование – постановка задачиПример 1. Производственная задача.
- 5. Графическое представление задачи линейного программированияУсловия производственной задачи
- 6. Графическое представление задачи линейного программирования. Примерограничения по
- 7. Линейное программирование. Продолжение примераОграничения по труду, как
- 8. Линейное программирование. Продолжение примераИз анализа результатов рис.1
- 9. Линейное программирование. Продолжение примера
- 10. Линейное программирование. Продолжение примераОбъединение ограничений рис. 1
- 11. Линейное программирование. Продолжение примераМаксимальное (или минимальное )
- 12. Двойственная задачаДвойственная задача. Каждой задаче линейного программирования
- 13. Методы решения задач линейного программирования. Методы решения
- 14. Симплекс метод1.Один из первых специализированных методов оптимизации,
- 15. Симплекс метод. Пример 2Предприятие может выпускать автоматические
- 16. Симплекс метод. Продолжение примера 2Для удобства восприятия
- 17. Симплекс метод. Продолжение примера 2После исключения неравенств
- 18. Симплекс метод. Продолжение примера 2После ввода новых
- 19. Симплекс метод. Продолжение примера 2Х1 / 200 + Х2 /
- 20. Симплекс метод. Продолжение примера 2Х1 + 2/3 Х2 +
- 21. Симплекс метод. Продолжение примера 2Х1 +
- 22. Транспортная задачаТранспортная задача–одна из задач линейного программирования.Ее
- 23. Транспортная задача. Пример 3Исходные данные к транспортной
- 24. Транспортная задача. Пример 3Надо спланировать перевозки, т.е.
- 25. Транспортная задачаКоличество переменных и ограничений в транспортной
- 26. Скачать презентанцию
Оптимизация. Постановка задачиЛинейное программирование как научно-практическая дисциплина. Из всех задач оптимизации задачи линейного программирования выделяются тем, что в них ограничения - системы линейных неравенств или равенств. Ограничения задают выпуклые линейные многогранники
Слайды и текст этой презентации
Слайд 1Методы оптимальных решений
Основные темы дисциплины
Оптимизация – постановка задачи
Линейное программирование и
задача оптимизации. Методы решения
Слайд 2Оптимизация. Постановка задачи
Линейное программирование как научно-практическая дисциплина. Из всех задач
оптимизации задачи линейного программирования выделяются тем, что в них ограничения
- системы линейных неравенств или равенств. Ограничения задают выпуклые линейные многогранники в конечном линейном пространстве. Целевые функции также линейны.Впервые такие задачи решались советским математиком Л.В. Канторовичем (1912-1986) в 1930-х годах как задачи производственного менеджмента с целью оптимизации организации производства и производственных процессов, например, процессов загрузки станков и раскройки листов материалов. После второй мировой войны аналогичными задачами занялись в США. В 1975 г. Т. Купманс (1910-1985, родился в Нидерландах, работал в основном в США) и академик АН СССР Л.В. Канторович были награждены Нобелевскими премиями по экономике.
Слайд 3Линейное программирование
Наиболее часто используются оптимизационные модели принятия
решений. Их общий вид
таков:
F (X) → max
X Є A
Здесь F – целевая функция; Х
– управляющий параметр, который может иметь различную природу - число, вектор, множество и т.п.
Цель менеджера - максимизировать целевую функцию F (X),
выбрав соответствующий Х, соответствующий множеству
определения А, X Є A .
Линейное программирование является одним из наиболее широко
применяемых методов оптимизации.
Слайд 4Линейное программирование – постановка задачи
Пример 1. Производственная задача. Цех может производить
стулья
и столы. На производство стула идет 5 единиц материала,
на
производство стола - 20 единиц. Стул требует 10 человеко-часов, стол - 15. Имеется 400 единиц материала и 450 человеко-
часов. Прибыль при производстве стула - 45 денежных единиц,
при производстве стола - 80 ден. ед.
Сколько надо сделать стульев и столов, чтобы получить
максимальную прибыль?
Обозначим: Х1 - число изготовленных стульев, Х2 - число
сделанных столов. Задача оптимизации (целевая функция) имеет
вид: F(x1,x2) = 45 Х1 + 80 Х2 → max ,
Ограничения задачи , т.е. допустимое множество Х
5 Х1 + 20 Х2 ≤ 400
10 Х1 + 15 Х2 ≤ 450
Х1 ≥ 0
Х2 ≥ 0
Слайд 5Графическое представление задачи линейного программирования
Условия производственной задачи можно изобразить на
координатной плоскости, откладывая по оси абсцисс значения Х1 , а
по вертикальной оси ординат - значения Х2. Тогда ограничения по
материалу и последние две строчки оптимизационной задачи
выделяют возможные значения (Х1 , Х2) объемов выпуска в виде
треугольника (рис.1).
Рис. 1. Ограничения по материалу
Слайд 6Графическое представление задачи линейного программирования. Пример
ограничения по материалу изображаются в
виде выпуклого
Многоугольника ( треугольника). Этот треугольник получается
путем отсечения
от первого квадранта примыкающей к началукоординат зоны. Отсечение проводится прямой, соответствующей
ограничениям 5 Х1 + 20 Х2 ≤ 400 и Х1 ≥ 0 , Х2 ≥ 0. При построении
эти неравенства заменяются на равенства.
Прямая пересекает ось Х1, соответствующую стульям, в точке
(80,0). Это означает, что если весь материал пустить на
изготовление стульев, то будет изготовлено 80 стульев. Та же
прямая пересекает ось Х2, соответствующую столам, в точке
(0,20). Это означает, что если весь материал пустить на
изготовление столов, то будет изготовлено 20 столов.
Для всех точек внутри треугольника выполнено неравенство, а не
равенство, а это означает, что материал останется.
Слайд 7Линейное программирование. Продолжение примера
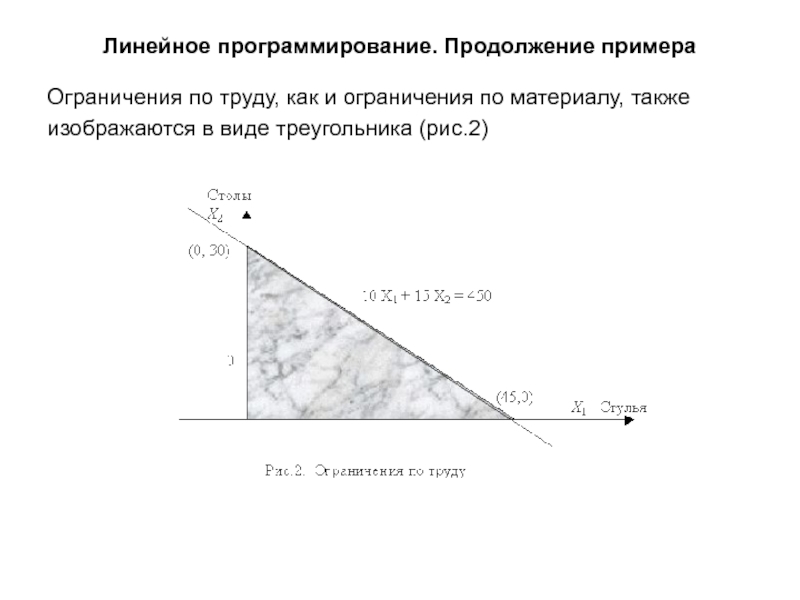
Ограничения по труду, как и ограничения по
материалу, также
изображаются в виде треугольника (рис.2)
Слайд 8Линейное программирование. Продолжение примера
Из анализа результатов рис.1 и рис.2 мы
видим, что очевидного
решения нет - для изготовления 80 стульев есть
материал, но не хватает рабочих рук, а для производства 30 столов есть рабочая
сила, но нет материала, Значит, надо изготавливать и то, и другое.
Но в каком соотношении?
Чтобы ответить на этот вопрос, надо "совместить" рис.1 и рис.2,
получив область возможных решений, а затем проследить, какие
значения принимает целевая функция на этом множестве (рис.3).
Слайд 10Линейное программирование. Продолжение примера
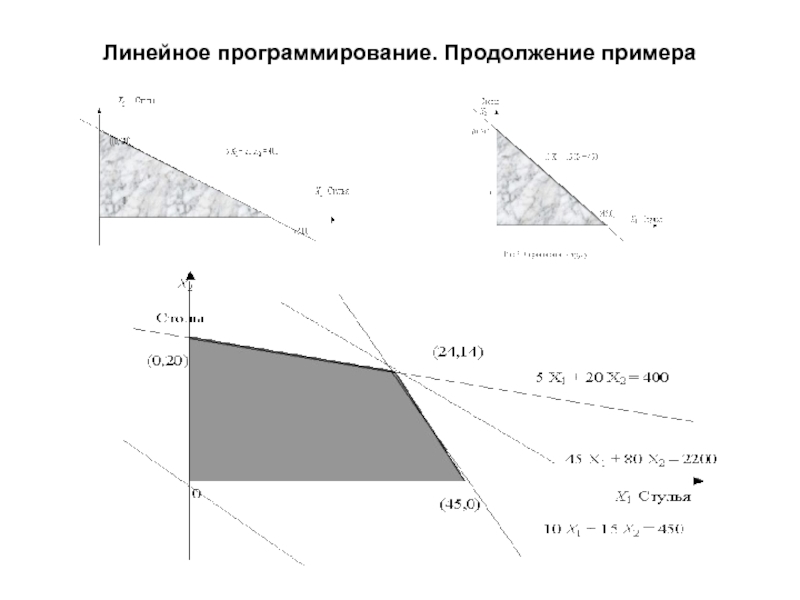
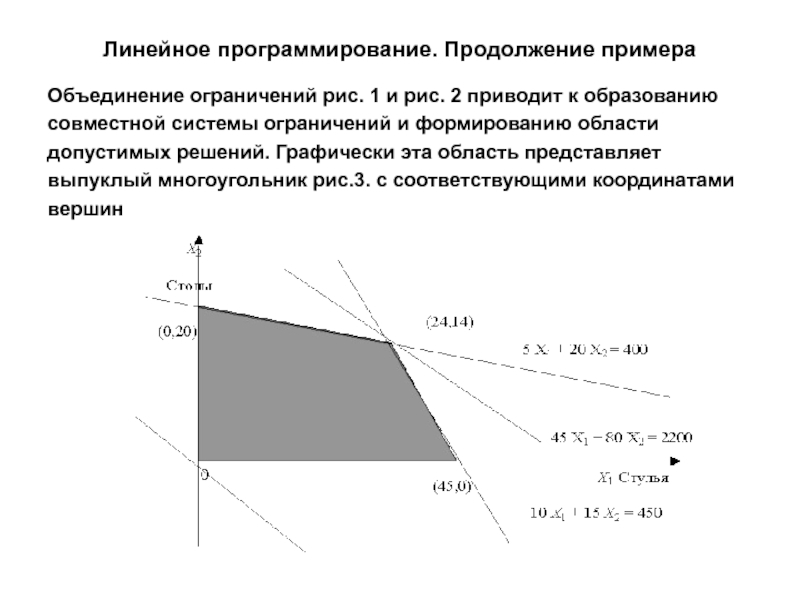
Объединение ограничений рис. 1 и рис. 2
приводит к образованию
совместной системы ограничений и формированию области
допустимых решений.
Графически эта область представляет выпуклый многоугольник рис.3. с соответствующими координатами
вершин
Слайд 11Линейное программирование. Продолжение примера
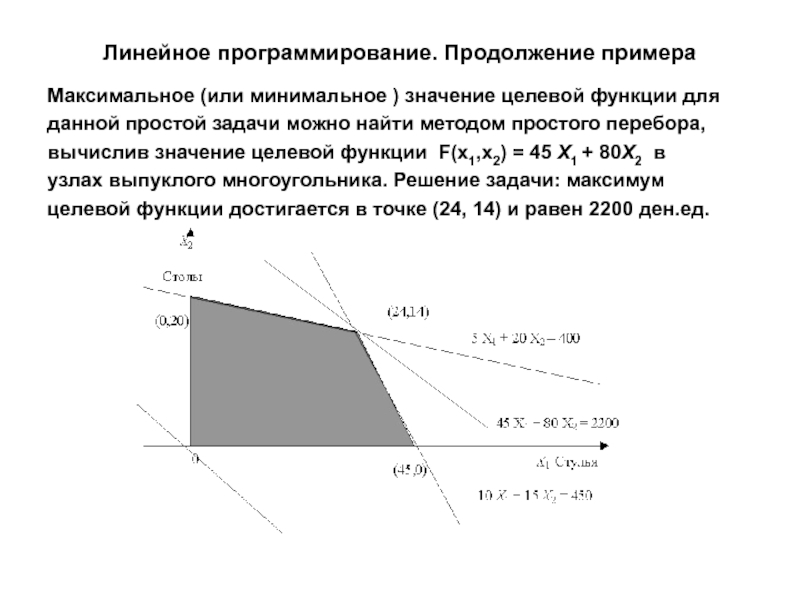
Максимальное (или минимальное ) значение целевой функции
для
данной простой задачи можно найти методом простого перебора,
вычислив
значение целевой функции F(x1,x2) = 45 Х1 + 80Х2 вузлах выпуклого многоугольника. Решение задачи: максимум
целевой функции достигается в точке (24, 14) и равен 2200 ден.ед.
Слайд 12Двойственная задача
Двойственная задача. Каждой задаче линейного программирования
соответствует двойственная задача.
В ней по сравнению с исходной
задачей строки переходят в столбцы,
неравенства меняют знак, Вместо максимума ищется минимум (или, наоборот, вместо
минимума –максимум). Задача, двойственная к двойственной – это
сама исходная задача.
Сравним исходную задачу (слева) и двойственную к ней (справа):
Прямая задача Двойственная задача
Целевая функция Целевая функция
F = 45Х1 + 80 Х2 → max , F= 400 W1 + 450 W2 → min ,
5 Х1 + 20 Х2 ≤ 400 , 5 W1 + 10 W2 ≥ 45,
10 Х1 + 15 Х2 ≤ 450 , 20 W1 + 15 W2 ≥ 80,
Х1 ≥ 0 , Х2 ≥ 0 . W1 ≥ 0, W2 ≥ 0.
Доказано, что оптимальные значения целевых функций в исходной и
двойственной задачах совпадают (т.е. максимум в исходной задаче
совпадает с минимумом в двойственной). оптимальные значения W1
W2 показывают стоимость материала и труда соответственно, если
Их оценивать по вкладу в целевую функцию их принято называть
"объективно обусловленными оценками" сырья и рабочей силы.
Слайд 13 Методы решения задач линейного программирования. Методы решения задач линейного программирования
относятся к вычислительной математике, а не к экономике и менеджменту.
Уметь пользоваться этим инструментом должен любой менеджер или инженер. Существуют программы, позволяющие автоматизировать решение этой задачи.Основными методами решения задачи линейного программирования являются:
1.Простой перебор.. Является методом графического решения задачи. Строится многоугольник области допустимых решений, в узлах этого прямоугольника вычисляется значение целевой функции, находятся координаты оптимального решения.
2. Направленный перебор. Строится линия целевой функции, которая переносится параллельно самой себе в направлении роста целевой функции. Находится вершина решения
Слайд 14Симплекс метод
1.Один из первых специализированных методов
оптимизации, нацеленный на решение
задач линейного
программирования.
2. Был предложен американцем Г. Данцигом в
1951 г. 3. Основная его идея состоит в продвижении по выпуклому
многограннику ограничений от вершины к вершине, при
котором на каждом шаге значение целевой функции
улучшается до тех пор, пока не будет достигнут оптимум.
Метод позволяет переходить от одного допустимого
базисного решения к другому, причем так, что значения
целевой функции непрерывно возрастают. В результате
оптимальное решение находят за конечное число шагов.
Алгоритмы симплекса-метода позволяют также установить,
является ли задача ЛП разрешимой.
Слайд 15Симплекс метод. Пример 2
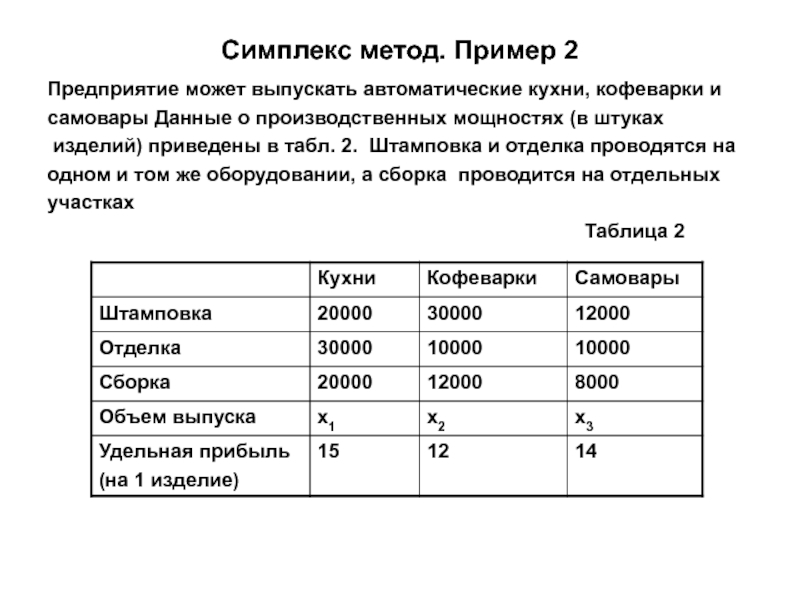
Предприятие может выпускать автоматические кухни, кофеварки и
самовары Данные о производственных мощностях (в штуках
изделий) приведены в
табл. 2. Штамповка и отделка проводятся на одном и том же оборудовании, а сборка проводится на отдельных
участках
Таблица 2
Слайд 16Симплекс метод. Продолжение примера 2
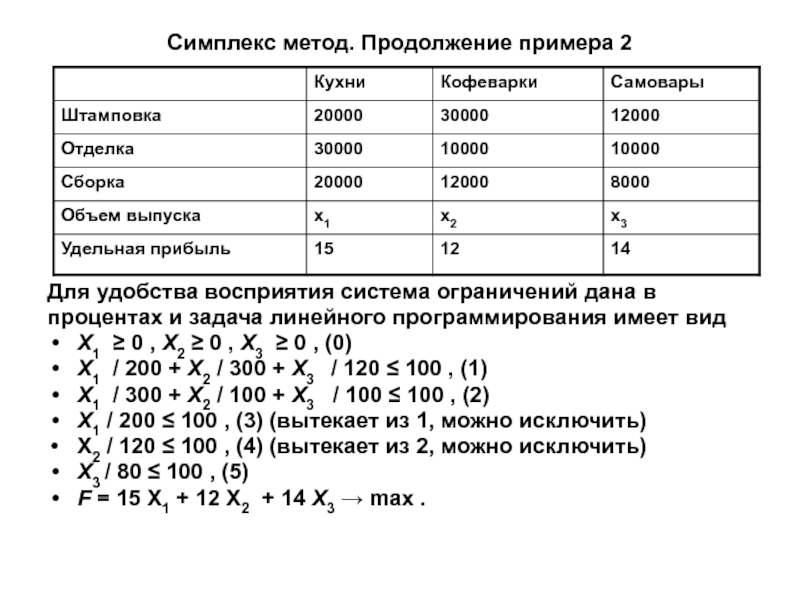
Для удобства восприятия система ограничений дана
в
процентах и задача линейного программирования имеет вид
Х1 ≥ 0 ,
Х2 ≥ 0 , Х3 ≥ 0 , (0)Х1 / 200 + Х2 / 300 + Х3 / 120 ≤ 100 , (1)
Х1 / 300 + Х2 / 100 + Х3 / 100 ≤ 100 , (2)
Х1 / 200 ≤ 100 , (3) (вытекает из 1, можно исключить)
Х2 / 120 ≤ 100 , (4) (вытекает из 2, можно исключить)
Х3 / 80 ≤ 100 , (5)
F = 15 Х1 + 12 Х2 + 14 Х3 → max .
Слайд 17Симплекс метод. Продолжение примера 2
После исключения неравенств (3) и (4)
задача линейного
программирования в окончательном варианте примет вид
F = 15 Х1
+ 12 Х2 + 14 Х3 → max .Х1 / 200 + Х2 / 300 + Х3 / 120 ≤ 100 (1),
Х1 / 300 + Х2 / 100 + Х3 / 100 ≤ 100 (2),
Х3 / 80 ≤ 100 (5)
В соответствии с симплекс методом, вводом новых переменных
система неравенств приводится в систему равенств. В конкретной
задаче вводятся 3 новых переменных.
В полученной системе равенств 3 уравнения и 6 неизвестных.
Система решается путем последовательного перебора базовых
переменных которая приводит к росту целевой функции
Слайд 18Симплекс метод. Продолжение примера 2
После ввода новых переменных система примет
вид
Х1 / 200 + Х2 / 300 + Х3 / 120 + Х4
= 100 Х1 / 300 + Х2 / 100 + Х3 / 100 + Х5 = 100 (*)
Х3 / 80 + Х6 = 100
15 Х1 + 12 Х2 + 14 Х3 = F
Симплекс метод – первая итерация
В данную систему переменные Х4 , Х5 , Х6 входят только в одно
из уравнений с коэффициентом 1 и являются базисными.
Свободные переменные Х1 , Х2 , , Х3 можно приравнять любой
константе, в том числе – нулю.
Тогда первое допустимое решение (0,0,0,100, 100, 100) , значение
целевой функции F =0.
Дальнейшая система пересчетов сводится к переводу одной из
свободных переменных в базис и с выводом одной из базисных
переменных и переводом ее в свободные переменные.
Слайд 19Симплекс метод. Продолжение примера 2
Х1 / 200 + Х2 / 300 + Х3
/ 120 + Х4
= 100Х1 / 300 + Х2 / 100 + Х3 / 100 + Х5 = 100 (**)
Х3 / 80 + Х6 = 100
15 Х1 + 12 Х2 + 14 Х3 = F
Симплекс метод – вторая итерация
1. В качестве новой базисной переменной выбираем Х1 –
переменную с наибольшим положительным коэффициентом в F .
2. Сравниваем частные от деления свободных членов на
коэффициенты при выбранной базисной переменной Х1 .
Получаем 100 / (1/200) = 20000, 100 / (1/300) =30000, 100/0 = + ∞.
Выбираем в системе строку, которая соответствует этому. Это –
первая строка. После ряда преобразований над системой (**)
получаем новую систему (***)
Слайд 20Симплекс метод. Продолжение примера 2
Х1 + 2/3 Х2 + 2/1,2 Х3
+ 200 Х4
= 200007/900 Х2 + 4/900 Х3 - 2/3 Х4 + Х5 = 100/3, (***)
Х3 / 80 + Х6 = 100
2 Х2 - 11 Х3 - 3000 Х4 = F – 300000
В новой системе базисными являются Х1 , Х5 , Х6 , свободными -
Х2, Х3 , Х4 . Второе допустимое решение (20000,0,0,0,100/3, 100)
Значение F = 300000.
Симплекс метод – вторая итерация
Так как наименьший положительный коэффициент в целевой
функции – при Х2, то выбираем Х2 базисной переменной. Проводя
аналогичные действия, образуем частные от деления свободных
членов на коэффициенты при Х2 , получаем
20000 / (2/3) = 30000, (100/3) / (7/900) = 30000/7, 100/0 = + ∞. В
качестве разрешающей выбираем вторую строку и после ряда
преобразований и пересчетов получаем систему (****) и целевую
функцию
Слайд 21Симплекс метод. Продолжение примера 2
Х1 +
9/7 Х3 + 1800/7 Х4 - 600/7 Х5
= 120000/7Х2 + 4/7 Х3 - 600/7 Х4 + 900/7 Х5 = 30000/7 (****)
Х3 / 80 + Х6 = 100
- 85/7 Х3 - 19800/7 Х4 - 1800/7 Х5 = F – 308571
Из (****) следует, что базисными переменными являются
Х1 =120000/7 , Х2 = 30000/7 , Х6 = 100 , F = 308571.
Так как в строке - 85/7 Х3 - 19800/7 Х4 - 1800/7 Х5 = F – 308571
не осталось ни одного положительного коэффициента, то
оптимальный план найден и производственная программа такая:
Кухни - 120000/7 = 17143
Кофемолки - 30000/7 = 4286
Самовары – 0
Максимальная прибыль – 308571 усл. ден. ед.
Все производственное оборудование будет задействовано за
исключением линии по сборке самоваров
Слайд 22Транспортная задача
Транспортная задача–одна из задач линейного программирования.
Ее цель – разработка
наиболее рациональных путей и способов
транспортировки товаров, устранения чрезмерно дальних,
встречных, повторных перевозок.
Разработка рациональных способов транспортировки товаров
позволяет сокращать время перевозок, расходы на
транспортировки, приводит к своевременной реализации
потребностей потребителя.
В зависимости от соотношения между суммарными запасами и
суммарными потребностями транспортные задачи могут быть
закрытыми и открытыми. Если сумма запасов груза равна
суммарной потребности в нем, то задача - закрытая , в противном
случае – открытая.
Математическая модель закрытой транспортной задачи – мини-
мизация целевой функции при заданных тарифах на перевозки
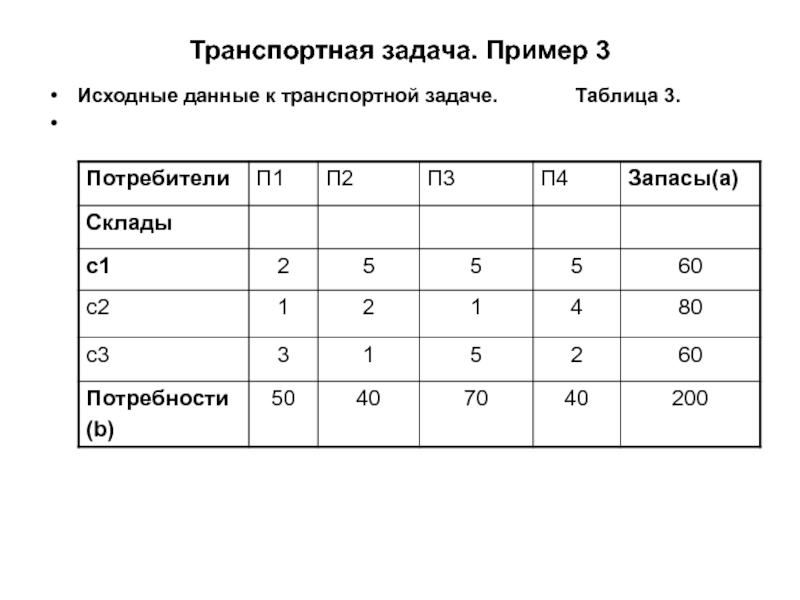
Слайд 24Транспортная задача. Пример 3
Надо спланировать перевозки, т.е. выбрать объемы
Хij поставок товара
со склада i потребителю j , где i = 1,2,3;
j = 1,2,3,4. Таким образом, всего в задаче имеется 12
переменных. Они удовлетворяют двум группам ограничений:
По запасам на складах: По ограничениям на потребление
X11 + Х12 + Х13 + Х14 = 60 , X11 + Х21 + Х31 = 50
X21 + Х22 + Х23 + Х24 = 80 , X12 + Х22 + Х32 = 40 ,
X31 + Х32 + Х33 + Х34 = 60 . X13 + Х23 + Х33 = 70 ,
X14 + Х24 + Х34 = 40
Всего 7 ограничений типа равенств. Кроме того, все переменные
неотрицательны - еще 12 ограничений.
Целевая функция - издержки по перевозке, которые необходимо
минимизировать:
F = 2 X11 + 5 Х12 + 4 Х13 + 5 Х14 + X21 + 2 Х22 + Х23 + 4 Х24 +
3 X31 + Х32 + 5 Х33 + 2 Х34 → min .
Слайд 25Транспортная задача
Количество переменных и ограничений в транспортной
задаче таково, что
ее следует решать с применением
современных программных продуктов. В учебных
задачах небольшого размера можно использовать метод потенциалов