Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ
Содержание
- 1. МЕТОДЫ СНИЖЕНИЯ РАЗМЕРНОСТИ
- 2. Метод среднего Строим функцию расстояния:Признаки упорядочиваются по величине . Строится последовательность:
- 3. Метод дивергенции Обобщенно это можно рассматривать как расстояние.Выбираем группу по максимуму.
- 4. Метод Фишера Берем следующую величину: и по данной величине определяем разбиение на классы.
- 5. Метод главных компонентМы строим новые последовательности множеств:
- 6. Для простоты считается , что =0 (этого
- 7. Оптимизационная задача решается с помощью метода градиента.Из
- 8. Следующий этап состоит в построении второй главной
- 9. В качестве выбирается следующее поле , то есть:Как найти вектор y?Мы должны построить матрицу:
- 10. Дальше можно поставить задачу выбора соответствующего количества
- 11. Скачать презентанцию
Метод среднего Строим функцию расстояния:Признаки упорядочиваются по величине . Строится последовательность:
Слайды и текст этой презентации
Слайд 2Метод среднего
Строим функцию расстояния:
Признаки упорядочиваются по величине . Строится
последовательность:
Слайд 3Метод дивергенции
Обобщенно это можно рассматривать как расстояние.
Выбираем группу по
максимуму.
Слайд 5Метод главных компонент
Мы строим новые последовательности множеств:
(х1,х2,х3,…,хn).
(y1,y2,y3,…,yr); n ≥
r.
Строим новую систему координат таким образом, чтобы дисперсия данных была
максимальной. В основе лежит анализ наших данных:
Слайд 6Для простоты считается , что =0 (этого можно добиться путем
центрирования):
Первая главная компонента строится следующим образом:
Мы ищем главную компоненту.
Сначала мы
должны найти -которая дает максимум дисперсии, при условиях того, что:
Слайд 7Оптимизационная задача решается с помощью метода градиента.
Из набора λI мы
должны взять число, которое дает нам максимум дисперсии.
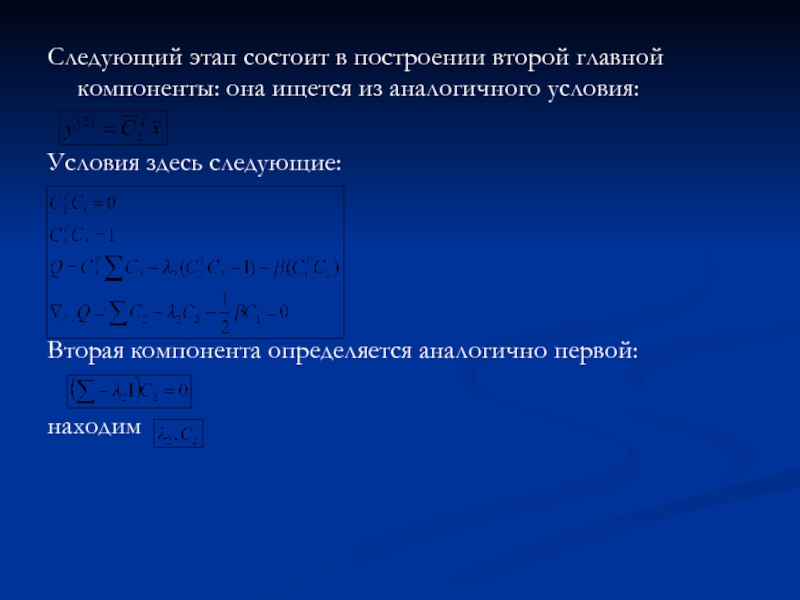
Слайд 8Следующий этап состоит в построении второй главной компоненты: она ищется
из аналогичного условия:
Условия здесь следующие:
Вторая компонента определяется аналогично первой:
находим
Слайд 9В качестве выбирается следующее поле , то есть:
Как
найти вектор y?
Мы должны построить матрицу:
Слайд 10Дальше можно поставить задачу выбора соответствующего количества признаков.
Где -
количество признаков.
Задав определенный уровень, мы можем выбрать нужное
количество компонентов.