Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы точечного оценивания
Содержание
- 1. Методы точечного оценивания
- 2. Задачей оптимизации в математике, информатике и исследовании операций называется задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.
- 3. Методы точечного оценивания с использованием полиномов и
- 4. Метод Пауэлла1. Задать x1 и шаг dx2. Найти x2 = x1
- 5. Метод Ньютона-РафсонаПусть f(x) - непрерывная и дважды дифференцируемая функция.Требуется
- 6. Метод средней точкиОпределяются две точки L, R в которых
- 7. Метод секущихМетод ориентирован на нахождение решения уравнения f’(x)
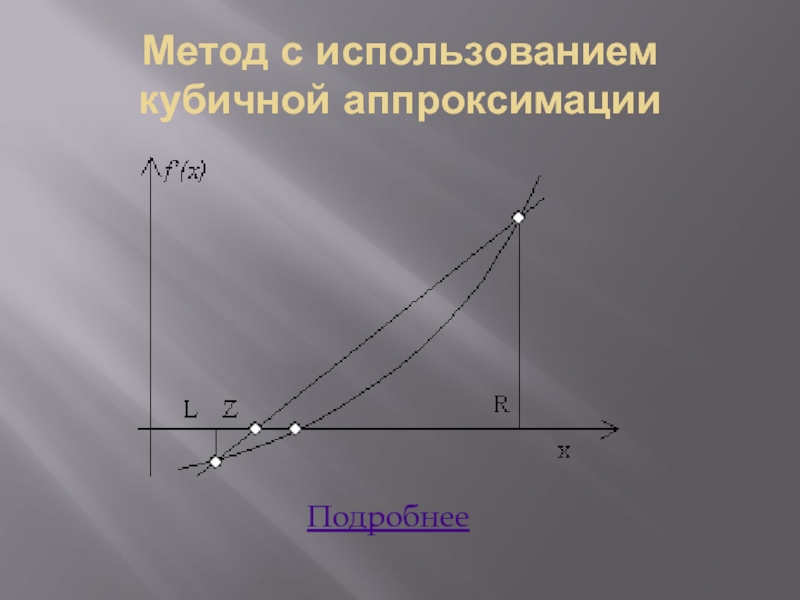
- 8. Метод с использованием кубичной аппроксимацииПодробнее
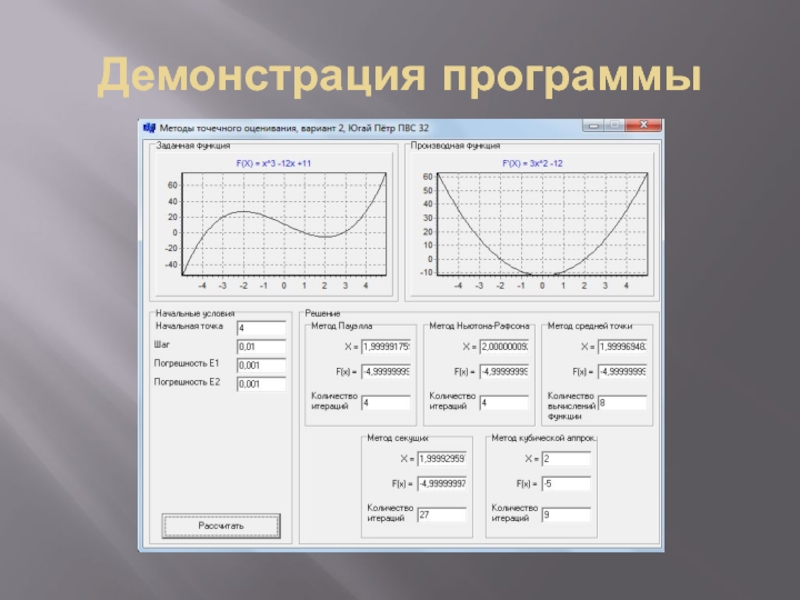
- 9. Демонстрация программы
- 10. Спасибо за внимание!
- 11. Скачать презентанцию
Задачей оптимизации в математике, информатике и исследовании операций называется задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.
Слайды и текст этой презентации
Слайд 1Методы точечного оценивания с использованием полиномов и методов с использованием
производных
Слайд 2Задачей оптимизации в математике, информатике и исследовании операций называется задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или
нелинейных
равенств и/или неравенств.
Слайд 3Методы точечного оценивания с использованием полиномов и методов с использованием
производных:
метод Пауэлла
метод Ньютона-Рафсона
метод средней точки
метод секущих
метод с использованием кубичной
аппроксимации.Слайд 4Метод Пауэлла
1. Задать x1 и шаг dx
2. Найти x2 = x1 + dx. Вычислить
f(x1) и f(x2).
3. Если f(x1) > f(x2) то x3 = x1 + 2dx иначе
x3
= x1 - dx.4. Вычислить f(x3); Fmin = min(f(x1), f(x2), f(x1)); Xmin
5. Найти x.
6. Проверка на окончание поиска. Если условия выполняются, то поиск окончен, иначе перейти к п. 7.
7. Принять за x1 наилучшую из точек x и Xmin. Перейти к п. 2.
Слайд 5Метод Ньютона-Рафсона
Пусть f(x) - непрерывная и дважды дифференцируемая функция.
Требуется найти корень уравнения f’(x)
= 0.
Зададим x1 – начальную точку поиска. Построим линейную аппроксимацию функции
f’(x) в точке x1. Для этого разложим f’(x) в ряд Тейлора в точке x1 и отбросим все члены второго порядка и выше.Подробнее
Слайд 6Метод средней точки
Определяются две точки L, R в которых производные имеют разные
знаки f’(L) < 0, f’(R) > 0. Искомый оптимум находится
между ними. Делим интервал пополам:Z = (L + R)/2.
Если f’(Z) > 0 то исключаем (Z,R). Если f’(Z) < 0 то исключаем (L,Z).
Алгоритм поиска минимума на (a, b).
1. L = a; R = b; f’(a) < 0; f’(b) > 0
2. Вычислить Z; f’(Z);
3. Если |f’(Z)|≤ ε, то закончить поиск.
4. Исключить соответствующий интервал. Перейти к п.2.
Слайд 7Метод секущих
Метод ориентирован на нахождение решения уравнения f’(x) = 0 на заданном
интервале (a, b). Метод похож на метод Ньютона, но строится не
касательная, а секущая.Z = R – f’(R)/ ([f’(R) – f’(L)] / (R - L))
В отличие от метода средней точки метод секущих использует информацию не только о знаке производной, но и о значениях в пробных точках.