Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ. МЕТОДЫ КВАЙНА И КВАЙНА-МАК-КЛАСКИ
Содержание
- 1. МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ. МЕТОДЫ КВАЙНА И КВАЙНА-МАК-КЛАСКИ
- 2. Цель лекции – изучить методы Квайна и
- 3. Литература Савельев А.Я. Прикладная теория цифровых автоматов.
- 4. Базовые понятия: Булева переменнаяБулева функцияДвоичная система счисленияЧисловое представление
- 5. Смысл процесса минимизации. 1Различные выражения одной и той же булевой функции описывают различные схемыПример
- 6. Смысл процесса минимизации. 2 Преобразуем СДНФ к
- 7. Определения Исходная функция задана в СДНФDef: импликанта
- 8. Историческая справкаКУАЙН Уиллард ван Онрман Американский математикПрофессор
- 9. Задача минимизации по методу Квайна
- 10. Задача минимизации по методу Квайна
- 11. Этапы метода КвайнаОпределение первичных импликантРасстановка метокНахождение существенных
- 12. Пример минимизации по методу Квайна Требуется минимизировать функцию: Представим функцию в виде СДНФ
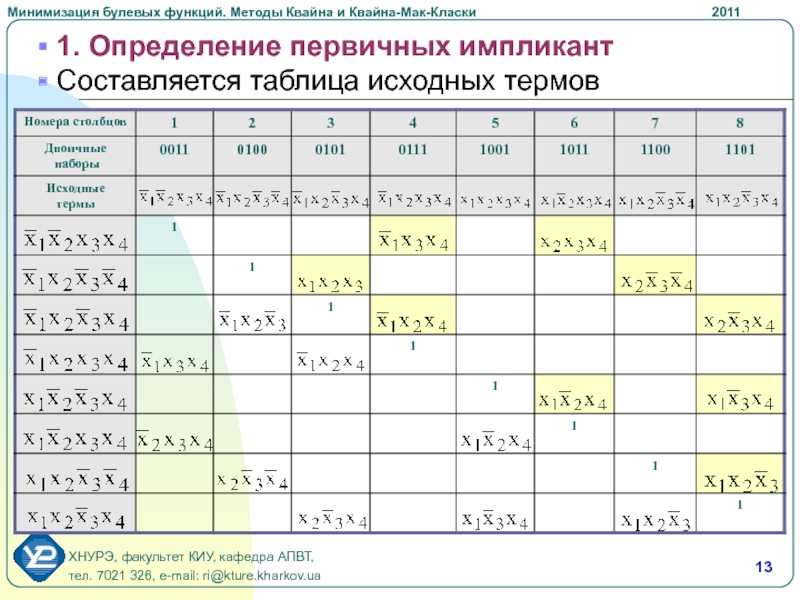
- 13. 1. Определение первичных импликант Составляется таблица исходных термов
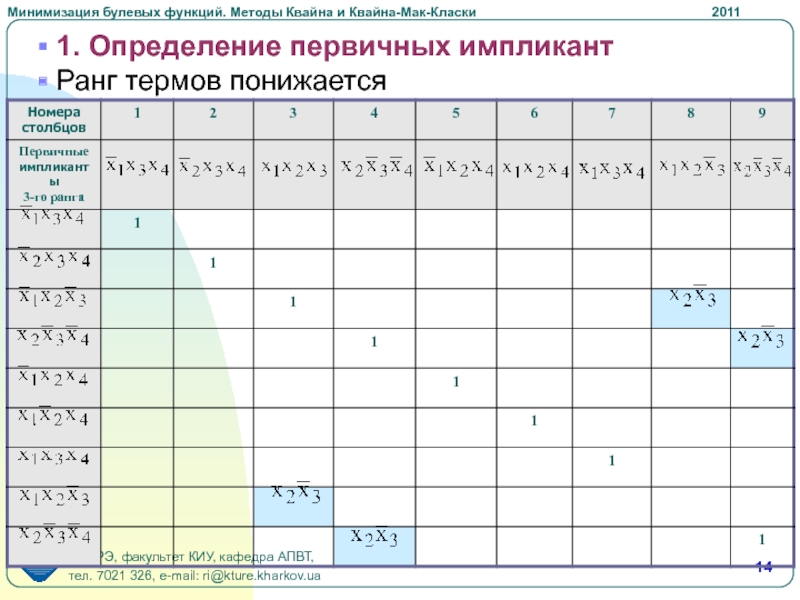
- 14. 1. Определение первичных импликант Ранг термов понижается
- 15. 2. Расстановка меток* ставится на пересечении
- 16. 3. Нахождение существенных импликантCущественной является импликанта, напротив которой в столбце стоит единственная *
- 17. 4. Удаление лишних столбцов 1Выделяются столбцы, в которых * стоит напротив существенной импликанты
- 18. 4. Удаление лишних столбцов 2Если в таблице
- 19. 5. Вычеркивание лишних первичных импликантЕсли после
- 20. 6. Выбор минимального покрытия 7. Составление
- 21. Недостаток метода КвайнаНеобходимость попарного сравнения всех термов
- 22. Time-Out
- 23. Метод Квайна-Мак-Класки – модификация метода КвайнаОсновывается на
- 24. Модификация метода Квайна – метод Квайна-Мак-Класки 2Исходные термы
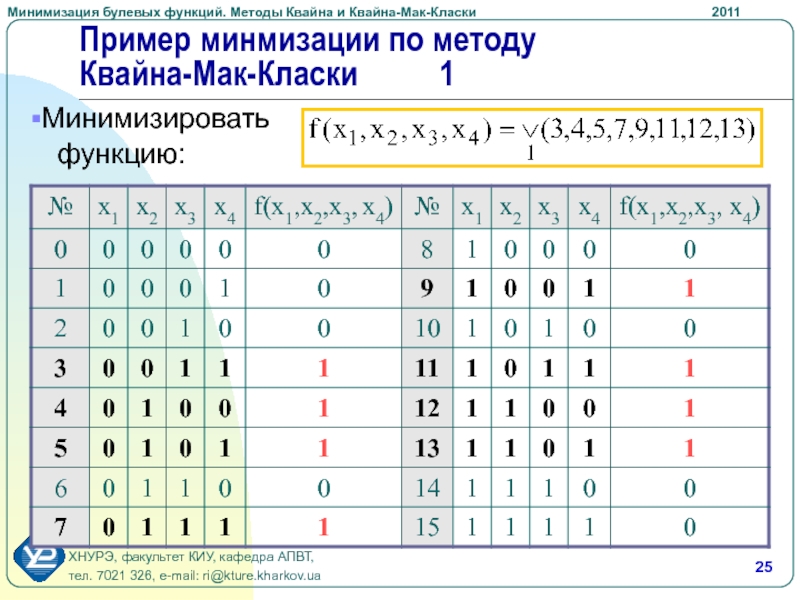
- 25. Пример минмизации по методу Квайна-Мак-Класки 1 Минимизировать функцию:
- 26. Пример минмизации по методу Квайна-Мак-Класки 2 Выпишем все 0-кубы (точки) в виде комплекса K0:
- 27. Пример минмизации по методу Квайна-Мак-Класки 3 Разобьем комплекс
- 28. Пример минмизации по методу Квайна-Мак-Класки 4 1. Определение
- 29. Пример минмизации по методу Квайна-Мак-Класки 5 По результатам склеивания составляем K123 куб: Склеивание кубов
- 30. Пример минмизации по методу Квайна-Мак-Класки 6 б) разбиваем
- 31. Пример минмизации по методу Квайна-Мак-Класки 7 Сравниваем кубы внутри каждой группы в целях получения K2-кубов:
- 32. Пример минмизации по методу Квайна-Мак-Класки 8 2. Составление
- 33. 3. Нахождение существенных импликант. Существенная имплитанта определяется
- 34. Пример минмизации по методу Квайна-Мак-Класки 9 A ν
- 35. ВыводыМетоды минимизации булевых функций используются во всех
- 36. Тест-вопросы1. Указать, какие кубы склеиваются: а) Х00,
- 37. Скачать презентанцию
Цель лекции – изучить методы Квайна и Квайна-Мак-Класки для минимизации булевых функций, описывающих комбинационные подсхемы цифровых проектов Содержание: Смысл процесса минимизации Понятие импликанты Этапы метода Квайна Недостатки метода Квайна Метод Квайна-Мак-Класки
Слайды и текст этой презентации
Слайд 2Цель лекции – изучить методы Квайна и Квайна-Мак-Класки для минимизации
булевых функций, описывающих комбинационные подсхемы цифровых проектов
Содержание:
Смысл
процесса минимизацииПонятие импликанты
Этапы метода Квайна
Недостатки метода Квайна
Метод Квайна-Мак-Класки
Примеры
Тема: Минимизация булевых функций.
Методы Квайна и Квайна-Мак-Класки
Слайд 3Литература
Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высш. шк.,
1987. 222-240 с.
Богомолов А.М., Сперанский Д.В. Аналитические методы в
задачах контроля и анализа дискретных устройств. Саратов: Изд-во Саратовкого ун-та, 1986. 240с.Хаханов В.И. Техническая диагностика элементов и узлов персональных компьюторов. К.: ИСМО, 1997. 308 с.
Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. С.35-43.
Слайд 4Базовые понятия:
Булева переменная
Булева функция
Двоичная система
счисления
Числовое представление ФАЛ
Кубическое представление ФАЛ
СДНФ
и СКНФ
Термины
Ключевые слова:
Минимизация
Импликанта
Существенные импликанты
Минимальное покрытие
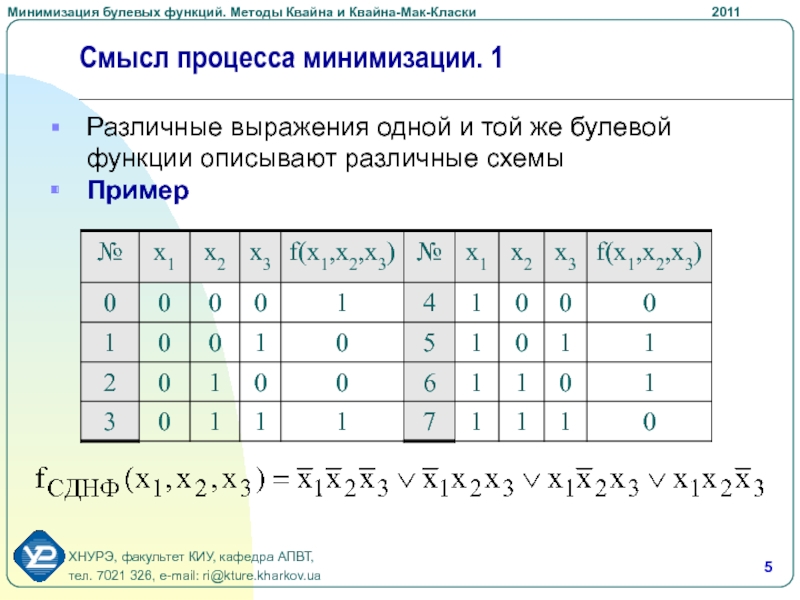
Слайд 5Смысл процесса минимизации. 1
Различные выражения одной и той же булевой
функции описывают различные схемы
Пример
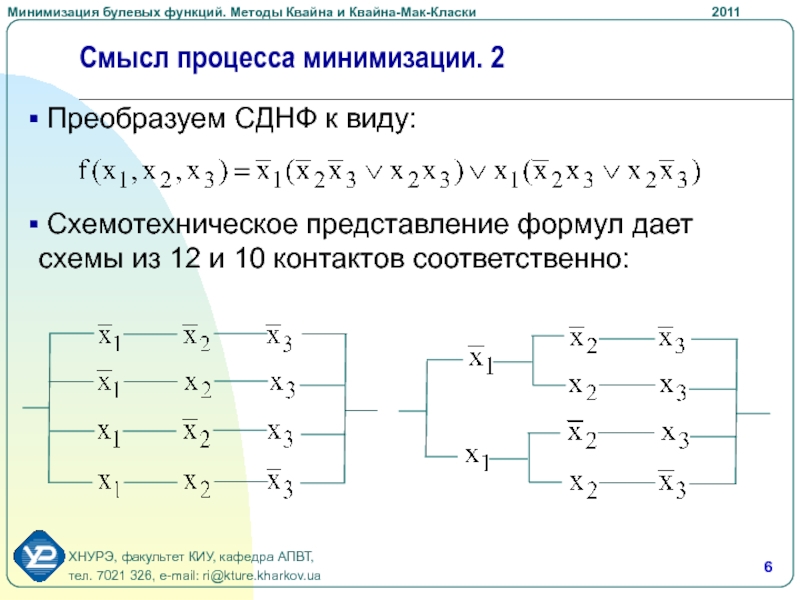
Слайд 6Смысл процесса минимизации. 2
Преобразуем СДНФ к виду:
Схемотехническое представление
формул дает схемы из 12 и 10 контактов соответственно:
Слайд 7Определения
Исходная функция задана в СДНФ
Def: импликанта функции – это
некоторая логическая функция, обращаемая в нуль на том же наборе
переменных, на котором равна нулю сама функцияЛюбой конъюнктивный терм или группа термов, соединенных знаками дизъюнкции, входящие в СДНФ, являются импликантами исходной функции
Def: первичная импликанта функции – это импликанта типа элементарной конъюнкции, никакая часть которой уже не является импликантой
Слайд 8Историческая справка
КУАЙН Уиллард ван Онрман
Американский математик
Профессор Гарвардского университета
Читал лекции
в Сан-Пауло (Бразилия), Оксфорде (Англия),
Токио, Париже, Упсале (Швеция)
Крупнейший
специалист в области математической логики и оснований математики Член Американской Академии наук и искусств в Бостоне
Слайд 9Задача минимизации по методу Квайна
1
Состоит в попарном сравнении всех импликант, входящих в СДНФ, в
целях выявления возможности поглощения какой-то переменной на основе закона склеиванияУдается понизить ранг термов
Процедура проводится до тех пор, пока не останется ни одного члена, допускающего поглощение с другим термом
Термы, подвергшиеся поглощению, отмечаются
Неотмеченные термы представляют собой первичные импликанты
Полученное логическое выражение не всегда оказывается минимальным
Слайд 10Задача минимизации по методу Квайна
2
Исследуется возможность дальнейшего упрощения
Составляется таблица, в строках
которой указываются найденные первичные импликанты, а в столбцах – термы исходного выражения Клетки таблицы отмечаются, если первичная импликанта входит в состав какого-либо терма
В итоге задача упрощения сводится к тому, чтобы найти такое минимальное количество первичных импликант, которые покрывают все столбцы
Слайд 11Этапы метода Квайна
Определение первичных импликант
Расстановка меток
Нахождение существенных импликант
Определение и удаление
лишних столбцов
Определение и удаление лишних первичных импликант
Выбор минимального покрытия
Составление минимальной
формы исходной функции
Слайд 12Пример минимизации по методу Квайна
Требуется минимизировать функцию:
Представим
функцию в виде СДНФ
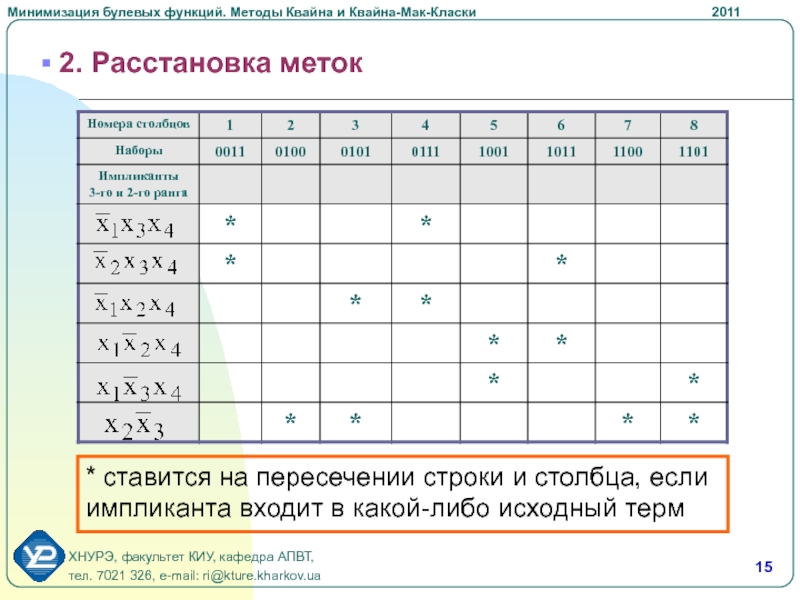
Слайд 15 2. Расстановка меток
* ставится на пересечении строки и столбца,
если импликанта входит в какой-либо исходный терм
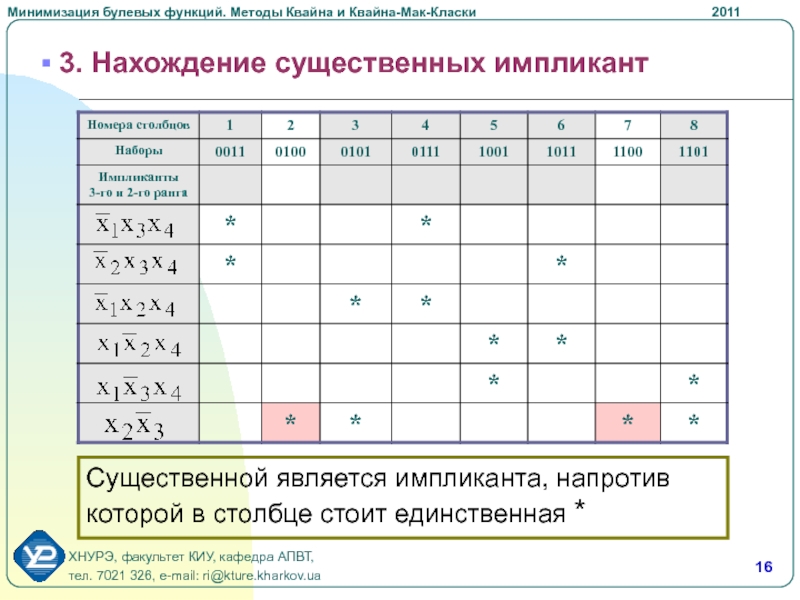
Слайд 16 3. Нахождение существенных импликант
Cущественной является импликанта, напротив которой в
столбце стоит единственная *
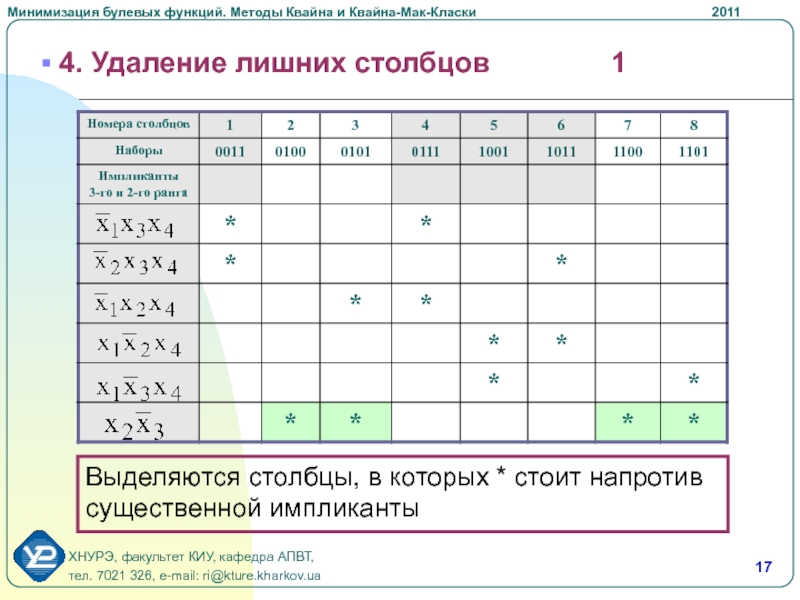
Слайд 17 4. Удаление лишних столбцов 1
Выделяются столбцы, в которых *
стоит напротив существенной импликанты
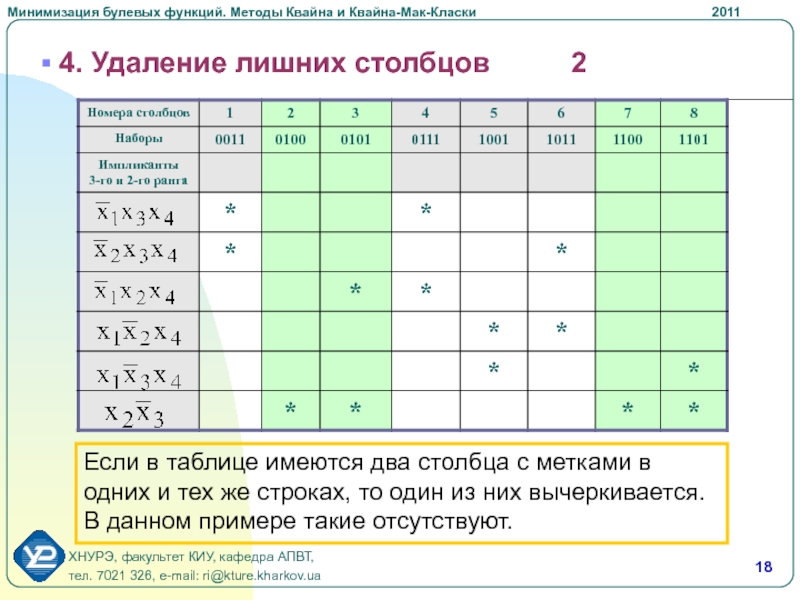
Слайд 18 4. Удаление лишних столбцов 2
Если в таблице имеются два столбца
с метками в одних и тех же строках, то один
из них вычеркивается. В данном примере такие отсутствуют.
Слайд 19 5. Вычеркивание лишних первичных
импликант
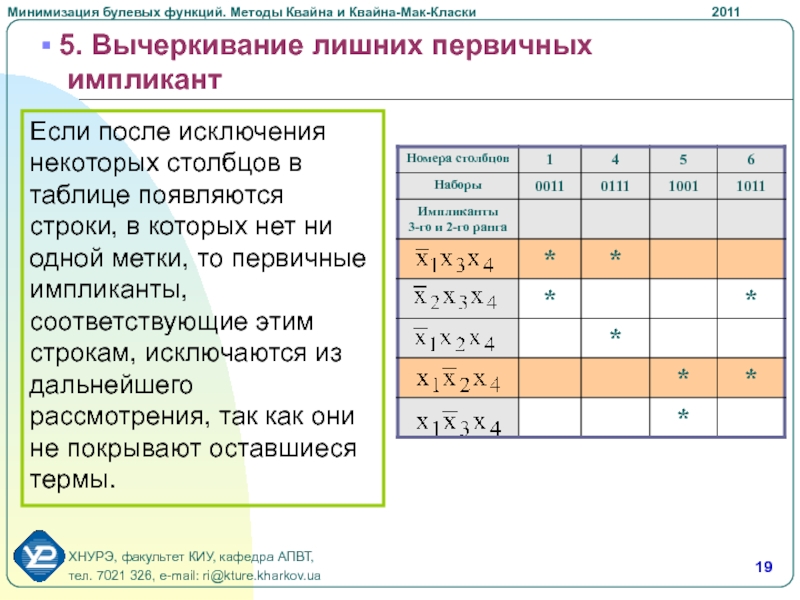
Если после исключения некоторых столбцов
в таблице появляются строки, в которых нет ни одной метки,
то первичные импликанты, соответствующие этим строкам, исключаются из дальнейшего рассмотрения, так как они не покрывают оставшиеся термы.
Слайд 20 6. Выбор минимального покрытия
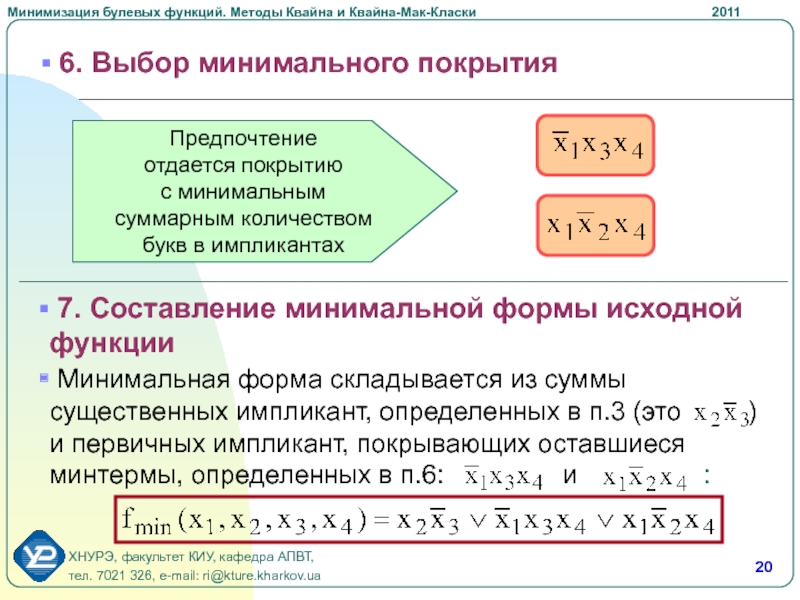
7. Составление минимальной формы исходной
функции
Минимальная форма складывается из суммы существенных импликант, определенных в
п.3 (это ) и первичных импликант, покрывающих оставшиеся минтермы, определенных в п.6: и :Предпочтение
отдается покрытию
с минимальным
суммарным количеством
букв в импликантах
Слайд 21Недостаток метода Квайна
Необходимость попарного сравнения всех термов на первом этапе
при нахождении первичных импликант
С ростом числа исходных термов увеличивается количество
попарных сравнений, что усложняет решениеВыход: модификация метода
Слайд 23Метод Квайна-Мак-Класки – модификация метода Квайна
Основывается на числовом и кубическом
представлении термов ДНФ
Числовое представление ФАЛ – упрощение процедуры нахождения первичных
импликант на первом этапе Исходное задание функции определяется для удобства десятичными кодами двоичных кубов, соответствующих ДНФ
Кубы предварительно разбиваются на подгруппы, определяемые одинаковым количеством единиц
Разбиение дает возможность сравнивать кубы только соседних по числу единиц групп для уменьшения количества переборов
Модификация метода Квайна – метод Квайна-Мак-Класки 1
Слайд 24Модификация метода Квайна – метод Квайна-Мак-Класки 2
Исходные термы записываются в виде
их двоичных номеров
Все номера разбиваются на непересекающиеся группы по
количеству единицУсловие образования r-куба – наличие расхождения в (r-1)-кубах только по одной координате в одном двоичном разряде и наличие общих независимых координат
В i-группу включают все номера наборов, имеющие в своей записи i единиц
Попарное сравнение проводится только между соседними по номеру группами
Слайд 26Пример минмизации по методу Квайна-Мак-Класки 2
Выпишем все 0-кубы (точки)
в виде комплекса K0:
Слайд 27Пример минмизации по методу Квайна-Мак-Класки 3
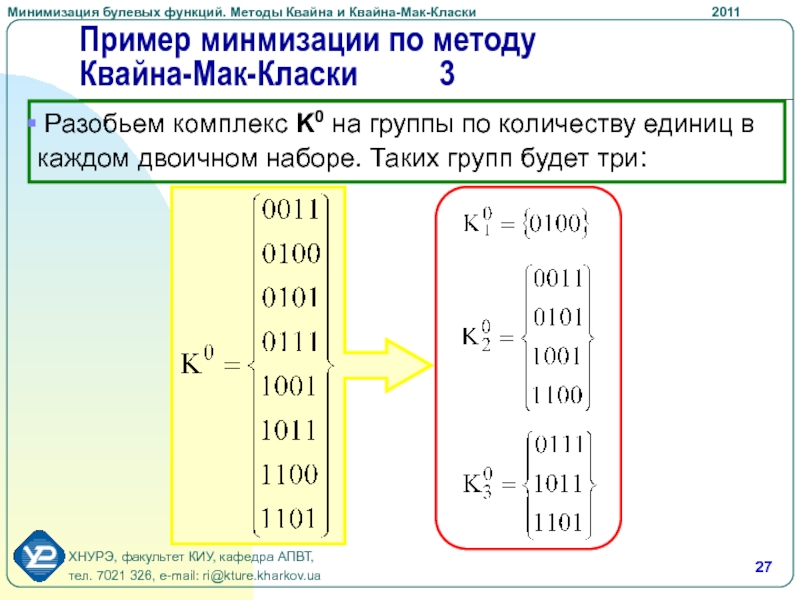
Разобьем комплекс K0 на
группы по количеству единиц в каждом двоичном наборе. Таких групп
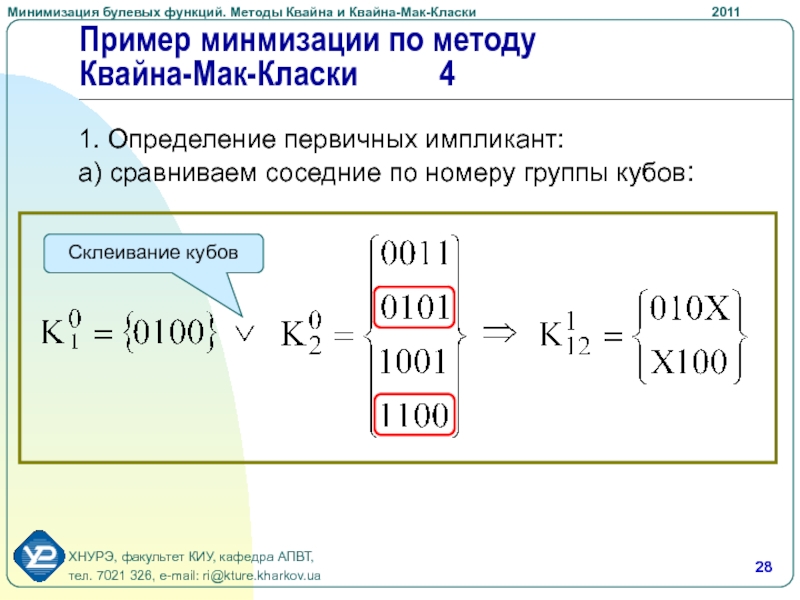
будет три:
Слайд 28Пример минмизации по методу Квайна-Мак-Класки 4
1. Определение первичных импликант:
а) сравниваем
соседние по номеру группы кубов:
Склеивание кубов
Слайд 29Пример минмизации по методу Квайна-Мак-Класки 5
По результатам склеивания составляем K123
куб:
Склеивание кубов
Слайд 30Пример минмизации по методу Квайна-Мак-Класки 6
б) разбиваем все 1-кубы на
группы в зависимости от положения независимых координат Х:
Нижний индекс
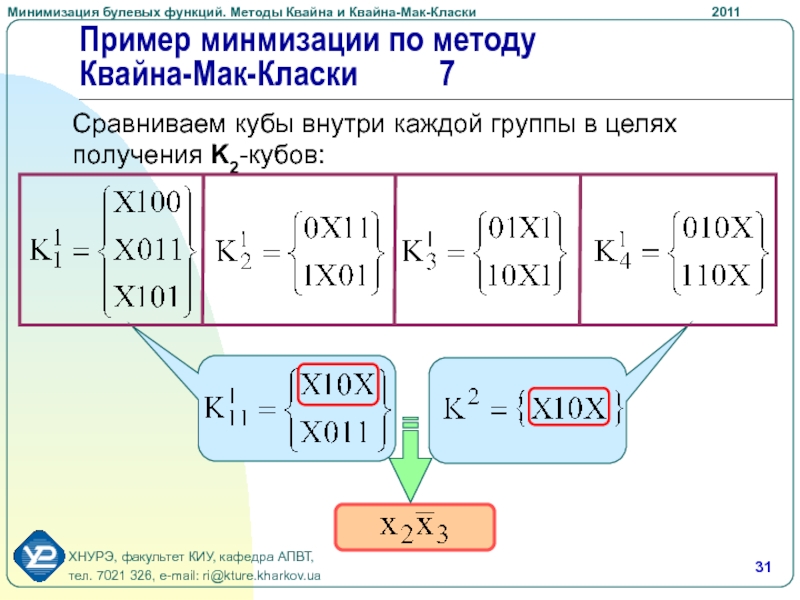
соответствует порядковому номеру расположения независимой координаты Х
Слайд 31Пример минмизации по методу Квайна-Мак-Класки 7
Сравниваем кубы внутри каждой группы
в целях получения K2-кубов:
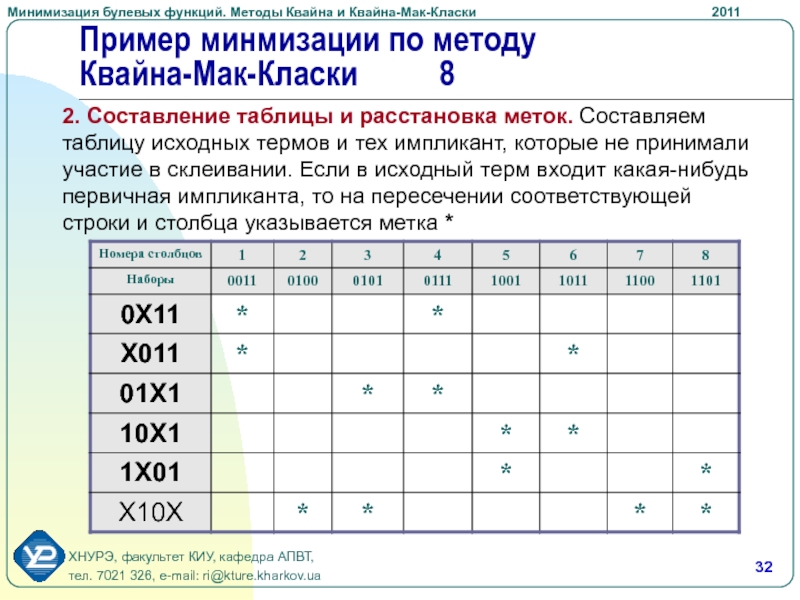
Слайд 32Пример минмизации по методу Квайна-Мак-Класки 8
2. Составление таблицы и расстановка
меток. Составляем таблицу исходных термов и тех импликант, которые не
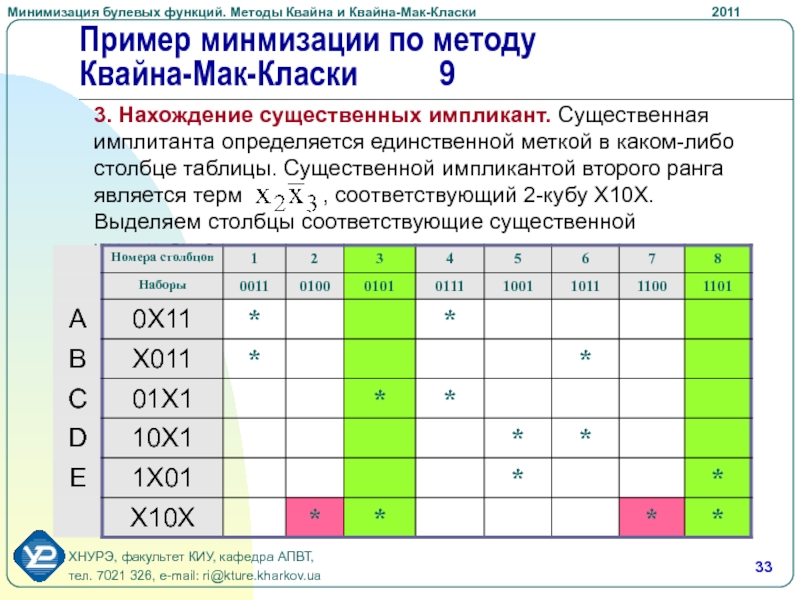
принимали участие в склеивании. Если в исходный терм входит какая-нибудь первичная импликанта, то на пересечении соответствующей строки и столбца указывается метка *
Слайд 333. Нахождение существенных импликант. Существенная имплитанта определяется единственной меткой в
каком-либо столбце таблицы. Существенной импликантой второго ранга является терм
, соответствующий 2-кубу Х10Х. Выделяем столбцы соответствующие существенной импликанте.Пример минмизации по методу Квайна-Мак-Класки 9
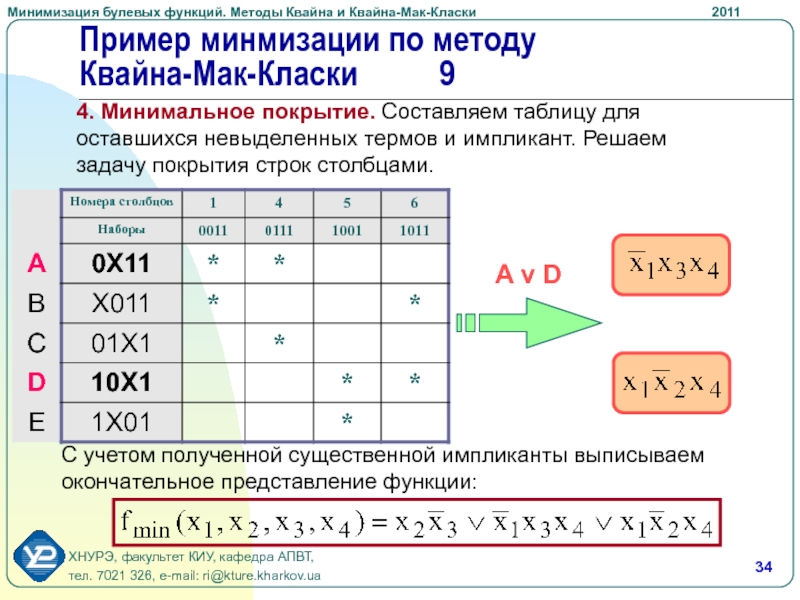
Слайд 34Пример минмизации по методу Квайна-Мак-Класки 9
A ν D
С учетом полученной
существенной импликанты выписываем окончательное представление функции:
4. Минимальное покрытие. Составляем таблицу
для оставшихся невыделенных термов и импликант. Решаем задачу покрытия строк столбцами.
Слайд 35Выводы
Методы минимизации булевых функций используются во всех программных приложениях, связанных
с синтезом вычислительных устройств
Они позволяют в среднем на 20-30% получить
более экономичный проект с позиции аппаратурных затратНаиболее практически ориентированным является метод Квайна-Мак-Класки, который оперирует кубическим представлением булевых функций
Недостатком обоих методов является применение импликантной таблицы для решения задачи нахождения минимального покрытия, которое требует большого объема памяти для реальных объектов
Слайд 36Тест-вопросы
1. Указать, какие кубы склеиваются:
а) Х00, Х10 ;
б) 011,
100;
в) 10Х, 01Х;
г) ни одна пара не склеивается.
2. Склеивание кубов
010 и 011 дает:а) Х00; б) 0ХХ;
в) 101; г) 01Х.
3. Куб ХХ1 является
а) 1-кубом; б) 2-кубом;
в) 0-кубом.
4. Куб 00Х является
а) 1-кубом;
б) 2-кубом;
в) 0-кубом.
5.Куб 011 является
а) 1-кубом;
б) 2-кубом;
в) 0-кубом.
6. Каждая импликанта в СДНФ соответствует
а) нулевому значению функции;
б) значению функции, равному единице.
7. Каждая импликанта в СКНФ соответствует
а) нулевому значению функции;
б) значению функции, равному единице.
