Слайд 1Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Владимирский государственный университет
имени Александра Григорьевича
и Николая Григорьевича Столетовых»
Педагогический институт
Кафедра "Педагогика и психология дошкольного и начального образования"
ПРЕЗЕНТАЦИЯ К ДОКЛАДУ ПО ДИСЦИПЛИНЕ
«АКТУАЛЬНЫЕ ПРОБЛЕМЫ МЕТОДИКИ ПРЕПОДАВАНИЯ МАТЕМАТИКИ
В НАЧАЛЬНЫХ КЛАССАХ»
НА ТЕМУ:
»РАЗВИТИЕ ПРОСТРАНСТВЕННОГО МЫШЛЕНИЯ МЛАДШИХ ШКОЛЬНИКОВ
НА ОСНОВЕ КОНСТРУИРОВАНИЯ»
Составила: студентка
гр. ЗНОу-117 Чернякова В.В.
Проверила: старший
преподаватель Болотова Т.В.
Владимир 2020
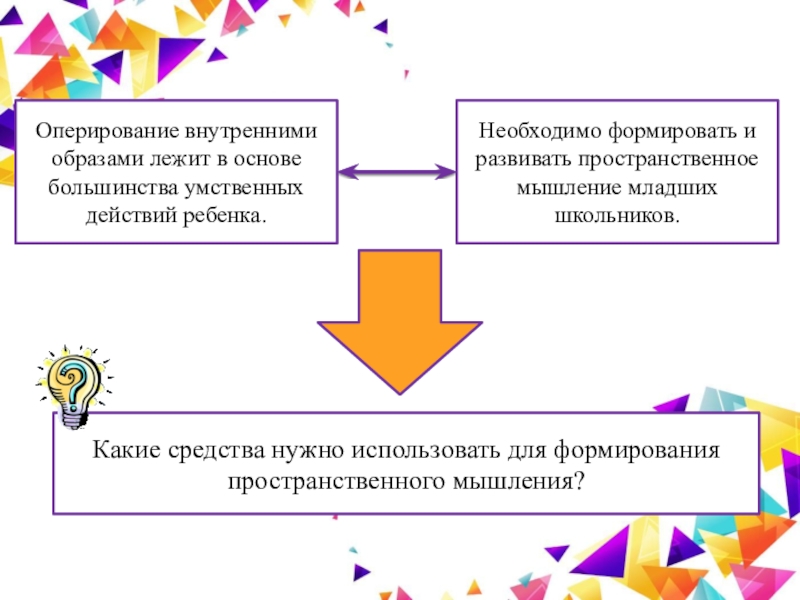
Слайд 2Оперирование внутренними образами лежит в основе большинства умственных действий ребенка.
Необходимо
формировать и развивать пространственное мышление младших школьников.
Какие средства нужно использовать
для формирования пространственного мышления?
Слайд 3«Пространственное мышление формируется в результате общего психического развития ребёнка, его
взаимодействия с окружающим миром, а также под влиянием обучения, в
ходе которого ученик познаёт пространственные свойства и пространственные отношения объектов»
доктор психологических наук, профессор И. С. Якиманская
Сенситивным периодом для развития пространственного мышления является возраст от 6 до 10 лет
Слайд 4Формируются пространственное мышление у учащихся 1-4 классов в процессе обучения
преимущественно путем:
Наблюдения;
Восприятия и осмысливания информации, полученной от учителя и
из учебников;
Практической деятельности (построение, рисование, моделирование и др.);
Мысленного оперирования пространственного мышления.
Слайд 5Умения в качестве критерия оценки сформированности
у учащихся пространственного мышления
по Н.Д. Мацько:
Распознавать данный объект среди объектов реальной деятельности.
Распознавать
объект среди изображений.
Устанавливать взаимосвязи между словом, представлением, изображением и объектом реальной деятельности.
Воспроизводить в воображении объект (представления памяти).
Воспроизводить представления памяти (словесно, графически, в виде модели).
Создавать в воображении новые объекты (представление воображения).
Воспроизводить представления воображения (словесно, графически, в виде модели).
1.
2.
3.
4.
5.
6.
7.
Слайд 6Уровни развития пространственного мышления у учащихся
1. Аккумулятивный
Накопление и узнавание
пространственных признаков и отношений.
Учащиеся накапливают разнообразные пространственные представления, учатся узнавать
разнообразные пространственные объекты, их отдельные признаки и отношения.
Слайд 7Уровни развития пространственного мышления у учащихся
2. Репродуктивный
Воспроизведение представления памяти.
У
учащегося развита способность воспроизводить
(в представлении, словесно, на рисунке, в
виде модели) известные им пространственные признаки и отношения.
Слайд 8Уровни развития пространственного мышления у учащихся
3. Конструктивный
Самостоятельное конструирование пространственного
образа.
Учащиеся на основе сформированных пространственных представлений создают новые представления и
оперируют ими, пользуясь словесным описанием, числовыми данными, рисунками.
Слайд 9Уровни развития пространственного мышления у учащихся
4. Интеллектуальный
Мысленное оперирование пространственными
образами
Для этого этапа характерно уже умение перемещать мысленно пространственные объекты
(симметрия, перенос, поворот), находить на рисунке положение фигуры после её перемещения, вид перемещения и т.д.
Слайд 10Конструирование «construere» в переводе с латинского языка, означает приведение в
определенный порядок и взаимоотношение различных отдельных предметов, частей, элементов, т.е.
подразумевает создание модели, построение чего-либо.
Конструктивное мышление позволяет видеть скрытые линии и части объекта, а также мысленно поворачивать, рассматривать с разных сторон, т.е. трансформировать его.
Это определение позволяет связать конструктивное мышление с пространственным мышлением, которое заключается в умение мысленно выстраивать какую-либо модель по заданным параметрам.
Слайд 11Л.А. Парамонова выделяет два типа конструирования:
Техническое
Художественное
− конструирование из строительного
материала;
− конструирование из деталей конструкторов;
− конструирование из крупногабаритных
модульных блоков.
− конструирование из бумаги;
− конструирование из природного материала.
Слайд 12Формы организации конструирования:
конструирование по образцу, разработанное Ф. Фребелем
Детям предлагают
образцы построек, показывают способы их воспроизведения.
1.
Слайд 13Формы организации конструирования:
− конструирование по модели, предложенное А.Н. Миреновой
и А.Р. Лурия
Детям в качестве образца предъявляют модель, которой очертание
отдельных ее элементов скрыто от ребенка, т.е. детям предлагают определенную задачу, но не дают способа ее решения.
2.
Слайд 14Формы организации конструирования:
конструирование по условиям предложено Н.Н. Поддьяковым
Ребенку даются
лишь условия, которым постройка должна соответствовать.
3.
Слайд 15Формы организации конструирования:
− конструирование по простейшим чертежам и наглядным
схемам разработанное С. Леона Лоренсо и В.В. Холмовской.
Детям предлагают чертежи
или схемы по которым дети должны сконструировать модель.
4.
Слайд 16Формы организации конструирования:
− конструирование по замыслу
Эффективность этого способа возможна
при наличии у детей обобщенных представлений о конструируемом объекте, обобщенных
способов конструирования и умения искать новые способы.
5.
Слайд 17Формы организации конструирования:
- конструирование по теме
Дети самостоятельно создают замыслы
конкретных построек и способы их выполнения.
6.
Слайд 18Формы организации конструирования:
− каркасное конструирование,
предложено Н.Н. Поддьяковым
В конструировании
такого типа ребенок должен домыслить разные дополнительные детали к каркасу.
7.
Слайд 19Методика работы с играми – головоломками по конструированию
В каждую собираемую
фигуру должны войти все ее элементы.
расположить фигуры нужно так,
чтобы они примыкали один к другому, а не накладывались друг на друга.
Правила игр:
Слайд 20Этапы работы с играми – головоломками
по конструированию
Знакомство с геометрическими
фигурами. Детям предлагаются упражнения, направленные на формирование представлений о геометрических
фигурах. Необходимо рассмотреть все геометрические фигуры, сосчитать, назвать их, сравнить по размеру, сгруппировать, отобрав все треугольники, четырехугольники и т.д. После этого предложить детям из набора фигур составить новые фигуры.
1.
Слайд 21Этапы работы с играми – головоломками
по конструированию
Детям раздаются карточки
с изображениями фигур, элементы фигуры представлены в натуральную величину. Учитель
вместе с учениками рассматривает расчлененный образец, и объясняет цель: составить такой же. Сначала составляют фигуру прямо на карточке с образцом. После успешного выполнения такого рода упражнений, детям можно предложить усложненное задание. Ученики получают образец с расчлененной фигурой, но уже не в натуральную величину и дается задание: составить данную фигуру.
2.
Слайд 22Этапы работы с играми – головоломками
по конструированию
Детям предлагают составить
фигуры силуэтов по контурным образцам из числа тех, что составлялись
ими ранее по расчлененным образцам.
Процесс составления фигуры при этом проходит на основе сформированного в начале зрительного анализа образца.
3.
Слайд 23Этапы работы с играми – головоломками
по конструированию
По мере освоения
детьми способов составления
фигур-силуэтов уместно предлагать им задания творческого характера,
стимулировать проявления смекалки, находчивости.
Усложнение заданий и изменение характера руководства со стороны педагога, повышение роли самостоятельных действий детей в ходе поисков составления фигуры помогают им овладевать более совершенными способами трансфигурации, на основании чего возможно конструирование предметных изображений по собственному замыслу.
4.
Слайд 24Игра «Танграм»
Танграм — старинная китайская игра-головоломка.
1.
2.
3.
4.
5.
Игра возникла около
4 тысяч лет назад.
Базовым элементом танграма является тан.
Таны возможно
получить при разрезании квадрата первоначально на два больших равных треугольника, далее согласно рисунка.
Минимальное количество базовых фигур равное семи приводит к гениальной простоте комбинаций.
Слайд 25Этапы работы с игрой «Танграм»
Знакомство с геометрическими фигурами, которые составляют
игру «Танграм»
1.
2.
Составление фигуры по расчлененному образцу натуральную величину.
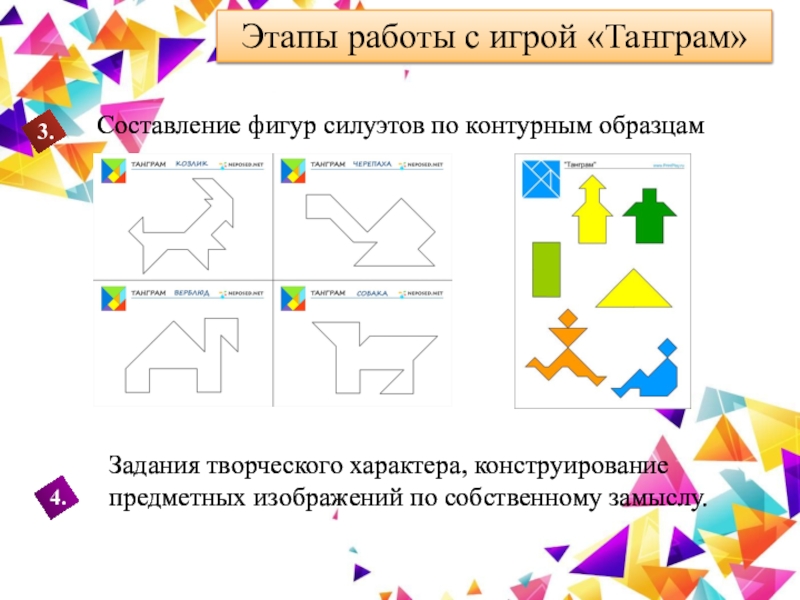
Слайд 26Этапы работы с игрой «Танграм»
Составление фигур силуэтов по контурным образцам
3.
4.
Задания
творческого характера, конструирование предметных изображений по собственному замыслу.
Слайд 27Игра «Пифагор»
Набор состоит из 7-ми геометрических фигур, полученных при делении
квадрата: 2 разных по размеру квадрата, 2 маленьких треугольника, 2
- больших (в сравнении с маленькими) и 1 четырехугольник (параллелограмм).
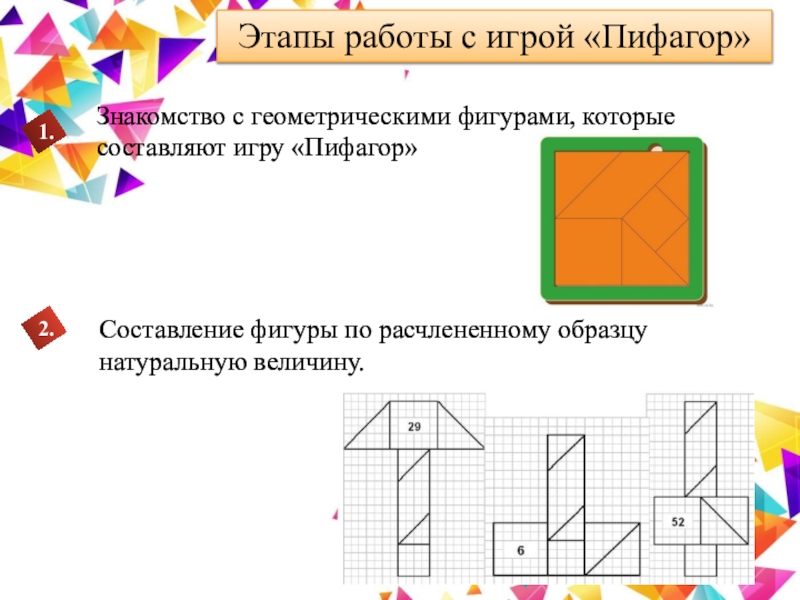
Слайд 28Этапы работы с игрой «Пифагор»
Знакомство с геометрическими фигурами, которые составляют
игру «Пифагор»
1.
2.
Составление фигуры по расчлененному образцу натуральную величину.
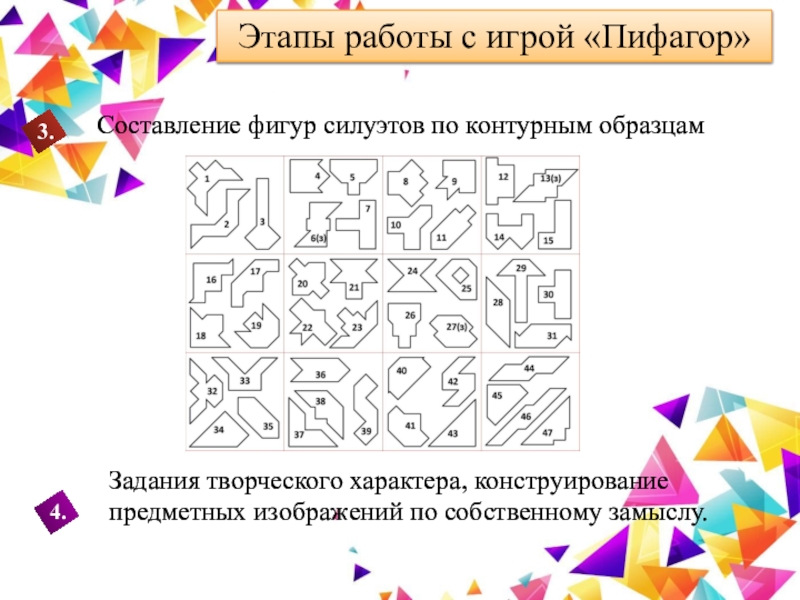
Слайд 29Этапы работы с игрой «Пифагор»
Составление фигур силуэтов по контурным образцам
3.
4.
Задания
творческого характера, конструирование предметных изображений по собственному замыслу.
Слайд 30«Монгольская игра»
Детская развивающая игра - головоломка "Монгольская игра". Квадрат, разделенный
на части по принципу «каждый раз пополам» (набор из 11-ти
фигур).
Слайд 31Этапы работы с «Монгольской игрой»
Знакомство с геометрическими фигурами, которые составляют
«Монгольскую игру»
1.
2.
Составление фигуры по расчлененному образцу натуральную величину.
Слайд 32Этапы работы с «Монгольской игрой»
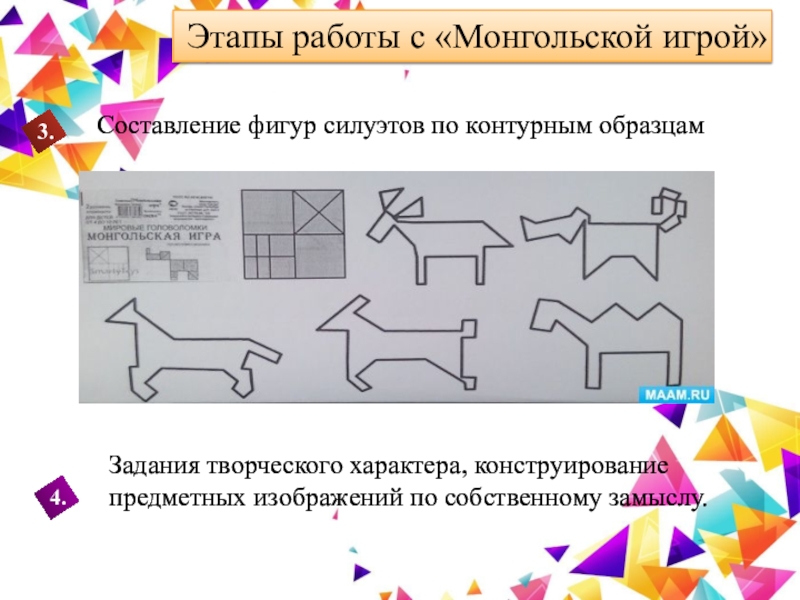
Составление фигур силуэтов по контурным образцам
3.
4.
Задания
творческого характера, конструирование предметных изображений по собственному замыслу.
Слайд 33Игра «Колумбово яйцо»
Название «Колумбово яйцо» очень подходит к данной головоломке.
В ней также приходится долго ломать голову над тем, как
сконструировать из 10 элементов яйца фигуру, а полученная в результате фигура обычно бывает очень проста.
Слайд 34Этапы работы с игрой «Колумбово яйцо»
Знакомство с геометрическими фигурами, которые
составляют «Колумбово яйцо»
1.
2.
Составление фигуры по расчлененному образцу натуральную величину.
Слайд 35Этапы работы с игрой «Колумбово яйцо»
Составление фигур силуэтов по контурным
образцам
3.
4.
Задания творческого характера, конструирование предметных изображений по собственному замыслу.
Слайд 36«Вьетнамская игра»
Детская развивающая игра – головоломка "Вьетнамская игра" представляет собой
7 замысловатых элементов с обтекаемыми контурами, получившиеся в результате деления
круга на части.
Слайд 37Этапы работы с «Вьетнамской игрой»
Знакомство с геометрическими фигурами, которые составляют
«Вьетнамскую игру»
1.
2.
Составление фигуры по расчлененному образцу натуральную величину.
Слайд 38Этапы работы с «Вьетнамской игрой»
Составление фигур силуэтов по контурным образцам
3.
4.
Задания
творческого характера, конструирование предметных изображений по собственному замыслу.
Слайд 39Игра «Волшебный круг»
Круг из 10 частей: среди которых 4 равных
треугольника, остальные части, попарно равны между собой, сходны с фигурами
треугольной формы, но одна из сторон у них имеет закругление.
Слайд 40Этапы работы с игрой «Волшебный круг»
Знакомство с геометрическими фигурами, которые
составляют «Волшебный круг»
1.
2.
Составление фигуры по расчлененному образцу натуральную величину.
Слайд 41Этапы работы с игрой «Волшебный круг»
Составление фигур силуэтов по контурным
образцам
3.
4.
Задания творческого характера, конструирование предметных изображений по собственному замыслу.
Слайд 42Игра «Пентамино»
Пентамино́ (от др.-греч. πέντα пять, и домино) — пятиклеточные
полимино, то есть плоские фигуры, каждая из которых состоит из
пяти одинаковых квадратов, которые требуется укладывать в прямоугольник или другие формы.
Слайд 43Игра «Пентамино»
Классификация по количеству квадратов в элементе
Из двух квадратов –
домино.
Из трех квадратов – тримино.
Из четырех квадратов – тетрамино.
Из пяти
квадратов – петамино.
Слайд 44Этапы работы с игрой «Пентамино»
Использование «Пентамино» в качестве геометрической мозаики.
1.
2.
Составление
фигуры по расчлененному образцу натуральную величину.
Слайд 45Этапы работы с игрой «Волшебный круг»
Составление фигур силуэтов по контурным
образцам
3.
4.
Собирание картинок по уменьшенному силуэтному изображению.
Слайд 46Сопоставительный анализ УМК на предмет содержания заданий на конструирование с
целью развития пространственного мышления
Слайд 51УМК «Школа России» пособие «Математика и конструирование» 1 класс
Слайд 52УМК «Школа России» пособие «Математика и конструирование» 2 класс
Слайд 53УМК «Школа России» пособие «Математика и конструирование» 3 класс
Слайд 54УМК «Школа России» пособие «Математика и конструирование» 4 класс
Слайд 55Выводы по УМК «Школа России»
Анализ содержательной стороны заданий из УМК
«Школа России» показал, что в учебниках встречаются задания на конструирование,
но чаще всего они однотипные. Отличным дополнением к учебнику является пособие С. И. Волковой «Математика и конструирование», которое может быть использовано на внеурочных занятиях. В этом пособии множество разнообразных упражнений на формирование и развитие пространственного мышления.
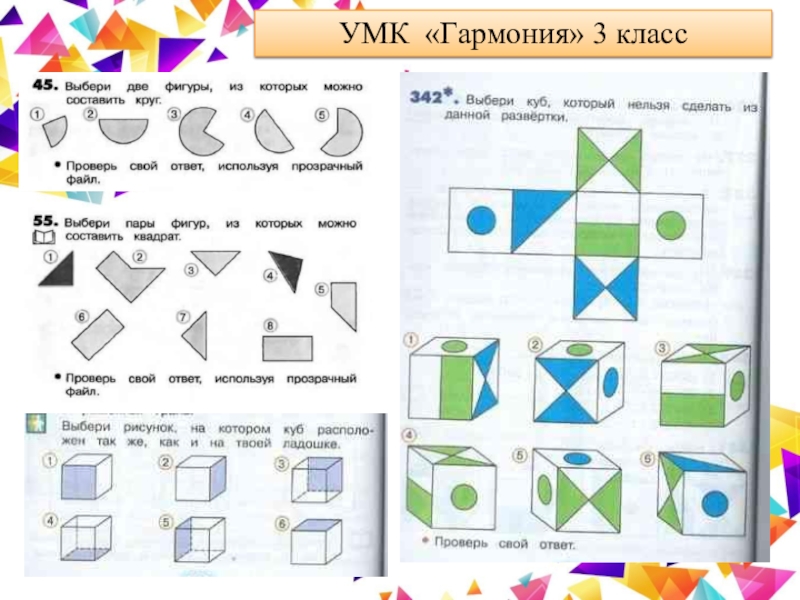
Слайд 59УМК «Гармония» пособие «Наглядная геометрия»
Слайд 60Выводы по УМК «Гармония»
Анализ содержательной стороны заданий показал, в программе
Н.Б. Истоминой (УМК «Гармония») сравнительно мало заданий на конструирование.
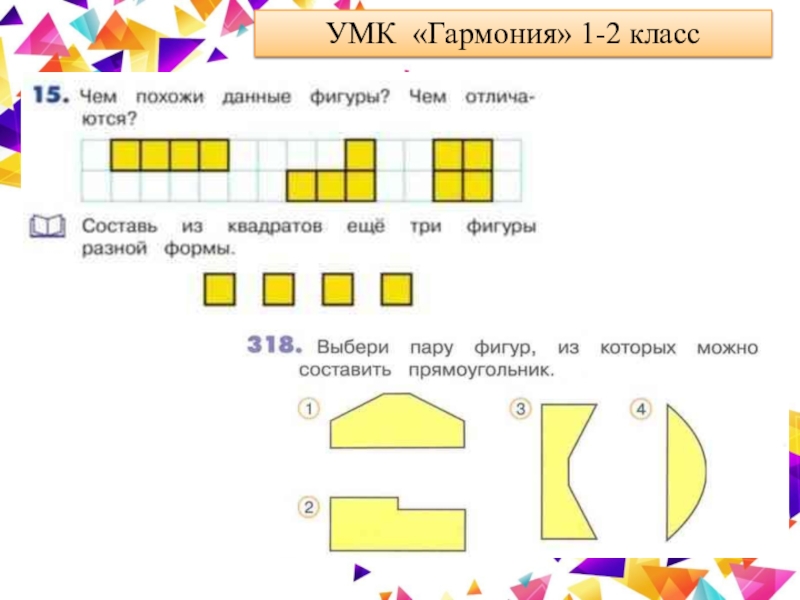
Встречаются 2
типа заданий:
-выбери две фигуры из которых можно составить круг(квадрат);
сделай развертку, вырежи ее и сконструируй куб (призму)
В пособии «Наглядная геометрия», разработанном Н.Б. Истоминой для занятий внеурочной деятельности, много заданий на развитие пространственного мышления, но крайне мало заданий на конструирование.
Слайд 61УМК «Система Л.В. Занкова» 4 класс 1 часть
Слайд 62УМК «Система Л.В. Занкова» 4 класс 2 часть
Слайд 63Выводы по УМК «Гармония»
Анализ содержательной стороны заданий показал, в учебниках
И.И. Аргинской особое внимание уделяется геометрическому материалу, способствующему развитию пространственного
мышления, но заданий на конструирование в учебниках 1-3 классов не встречается. В 4 классе автор учебника знакомит детей со старинной игрой «Танграм», дети по заданию учебника самостоятельно изготавливают эту игру, нумеруют детали «танграма» и учатся конструировать из элементов этой игры. Задания на конструирование с помощью «Танграма» встречаются на протяжении всего 4 класса в учебниках.