Многоэлектронные атомы. Взаимодействие атомов с излучением

физике ядра и ядерным реакциям
В.В.Самарин
2019
Государственный университет «Дубна» Факультет

естественных и инженерных наук
Кафедра Ядерной физики

терма. Сложение моментов. Приближение LS и jj-связей. Правила Хунда.
Нестационарная теория

возмущений. Золотое правило Ферми.
Вторичное квантование свободного электромагнитного поля. Взаимодействие атома с квантованным полем излучения.

конфигурация. Терм. Тонкая структура терма.
Сложение моментов.
Приближение LS связи.
Приближение jj-связи.

рентгеновской трубки 1 монохроматическое (называемое характеристическим) рентгеновское излучение
с длиной

волны λ0, проходит через свинцовые диафрагмы 2 и в виде узкого пучка направляется на рассеивающее вещество
– мишень 3. Излучение, рассеянное под некоторым углом θ, анализируется с помощью спектрографа рентгеновских лучей 4,
в котором роль дифракционной решетки играет кристалл 5, закрепленный на поворотном столике.

Спектры рассеянного рентгеновского излучения

Характеристическое рентгеновское излучение

Тормозное рентгеновское излучение

Тормозное рентгеновское излучение имеет сплошной спектр с минимальной длиной волны lmin

U – ускоряющее напряжение на рентгеновской трубке

σ (а).
Схематичный график эффективного
сечения фотоэффекта в зависимости от энергии g-кванта
Схематичный

график массового коэффициента поглощения для серебра и меди
в зависимости от длины волны рентгеновского излучения

Сечение σ определяется как отношение числа рассеянных (в других процессах – поглощенных) в единицу времени квантов к плотности потока квантов (числу квантов, проходящих в единицу времени через единицу площади).

При атомном фотоэффекте фотон поглощается атомом, после чего атом испускает электрон с одной из своих оболочек.

Вероятность внутреннего фотоэффекта максимальна при энергиях Еg порядка нескольких десятков кэВ (в частности, для характеристического рентгеновского излучения), а с возрастанием энергии гамма-кванта уменьшается приблизительно обратно пропорционально Еg .

взаимодействующих только с ядром
1
2
2
2
3
3
3
4
4
4
4
5
6
7

атом_ССП.pdf
Li+ 1s2
Na+ 1s22s22p6
K+ 1s22s22p63s23p6

атом_ССП.pdf

5
6
7
5
5

пример: атом гелия с двумя электронами. Основное состояние с симметричной координат- ной волновой функцией:

терм 1S, конфигурация 1s2.
Возбужденные состояния с конфигурацией 1s2s: терм 3S с меньшей энергией (ортогелий) с антисимметричной волновой
функцией, спином S=1, мультиплетностью 2S+1=3, L=0. Tерм 1S с большей энергией (парагелий) с симметричной волновой функцией, спином S=0, мультиплетностью 2S+1=1, L=0. Первое эмпирическое правило Хунда:
Из термов, принадлежащих данной электронной конфигурации, наименьшей энергией обладает терм с наибольшим возможным значением S и с наибольшим возможным при таком S значении L. Для такого терма электроны в среднем дальше друг от друга и энергия их отталкивания меньше.

и переходов между ними
S=1
S=0
формулы 18

между ними, в разрывах
стрелок указаны длины волн (в нм)

или цвета спектральных линий:
ж1 – одна из желтых линий,
з – зеленая, г – голубая,
сф – сине-фиолетовая,
ф1 – более яркая фиолетовая,
ф2 – более слабая фиолетовая

между ними, ж1 и ж2 –
две желтых линии
ж1
ж2
E
по jj-связи
по

L-S-связи

времени возмущении приближенное вычисление волновой функции Y(t) выполняют c помощью

разложения по волновым функциям стационарных состояний невозмущенной системы

Для j-го невозмущенного состояния, в котором система находилась при t  –,

коэффициенты разложения в первом приближении равны

По истечении времени действия возмущения (или в пределе t  ) коэффициенты akj принимают постоянные значения akj(), их квадраты модулей определяют вероятность оказаться в k-м стационарном состоянии с энергией

Вероятность перехода из начального состояния i в конечное состояние f

В пределе, при достаточно медленном (адиабатическом) изменении возмущения, модуль интеграла из-за быстро- осциллирующего знакопеременного множителя (экспоненты) очень мал, вероятность перехода стремится к нулю и система остается в первоначальном состоянии.

формулы 17

вычисление волновой функции Y(t) выполняют c помощью разложения по волновым

функциям стационарных состояний невозмущенной системы

Для j-го невозмущенного состояния

коэффициенты разложения в первом приближении равны

постоянного возмущения
Волновая функция системы разлагается по невозмущенным волновым функциям дискретного

спектра, нормированным на единицу, и по функциям непрерывного спектра, нормированным на d-функцию,

Дельта-функция устраняется при интегрировании по конечному интервалу состояний. Для невырожденных состояний непрерывного спектра dnf = dEf . Для плотности состояний r(Ef) (числа конечных состояний данного типа, приходящихся на единичный интервал энергий Ef) dnf = r(Ef) dEf:

Вероятность перехода в единицу времени (скорость перехода) из начального невозмущенного состояния i в конечное состояние f, в котором величины n имеют значения в интервале dnf под действием постоянного (не зависящего от времени) возмущения V:

при действии постоянного (не зависящего от времени) возмущения V коэффициенты разложения в первом приближении равны

формулы 17

Эта вероятность отлична от нуля лишь для переходов в состояния с энергией Ef = Ei в согласии с законом сохранения энергии.

Эту формулу Ферми назвал золотым правилом из-за ее исключительной важности и пользы.

двух слабо взаимодействующих частей в моменты времени t = 0

и t = Dt: e, E при t = 0, e’, E’ при t = Dt, вероятность перехода под действием не зависящего от времени возмущения пропорциональна величине

Наиболее вероятно значение не зависит от величины возмущения:

В квантовой механике закон сохранения энергии может быть проверен посредством двух измерений лишь с точностью до величины порядка где Dt  интервал времени между измерениями.

соотношение неопределенности для энергии

Энергию Е можно рассматривать как энергию некоторой системы, а e  как энергию измерительного прибора, которая известна точно (De=De’=0), тогда:

формулы 17

периодического возмущения
Волновая функция системы разлагается по невозмущенным волновым функциям дискретного

спектра, нормированным на единицу, и по функциям непрерывного спектра, нормированным на d-функцию,

Эта вероятность отлична от нуля лишь для переходов в состояния с энергией Ef=Ei в согласии с законом сохранения энергии. При возмущении ~exp(iwt) система теряет энергию (например, испускает фотон), а при возмущении ~exp(–iwt) увеличивает энергию (например, поглощает фотон).

Вероятность перехода в единицу времени (скорость перехода) из начального невозмущенного состояния i в конечное состояние f, в котором величины n имеют значения в интервале dnf под действием постоянного (не зависящего от времени) возмущения V

при действии периодически зависящего от времени между моментами включения и выключения возмущения V коэффициенты разложения в первом приближении равны

точностью до величины порядка , где

Dt = t  продолжительность жизни этого состояния системы, т.е. величина, обратная вероятности w распада в единицу времени Если Е0 начальная энергия системы, Е и e энергии частей, на которые распалась система, то

Энергия способной к распаду системы может быть определена лишь с точностью до величины порядка . Система, способная к распаду, не обладает строго дискретным спектром энергий, поскольку частица, уходящая на бесконечность имеет непрерывный спектр энергий (ее движение инфинитно). Если вероятность распада мала, например в случае потенциального барьера с малой проницаемостью, то состояние системы называется квазистационарным с квазидискретным спектром из ряда размытых уровней, ширины G, которых определяются их продолжительностью жизни и малы по сравнению с расстояниями между уровнями

Квазистационарные состояния

Серия физическая, 2014, т. 78, с. 1388–1395
Соотношение неопределенности для энергии
Dt

– время жизни состояния (характерное время распада),
DE – неопределенность энергии состояния

Волновая функция квазистационарного состояния при r→ представляет расходящуюся волну y ~ exp(ikr)/r.
На рис. 5 и 3 показаны плотности вероятности для функции c(r) = ry(r)

полем излучения.

поле описывают векторным потенциалом A в калибровке, в которой скалярный

потенциал равен нулю. Поле в большом объеме пространства W (например, кубе W = L3) можно разложить на бегущие плоские волны (в системе единиц, где скорость света равна 1)

Суммирование производится по дискретному набору значений компонент волнового вектора, таких, что exp(ikxL)=1, exp(ikyL)=1, exp(ikzL)=1 и один вектор приходится на объем (Dk)3 в пространстве волновых векторов

L

Канонические переменные поля (обобщенные координаты Q и обобщенные импульсы P ) и функция Гамильтона (энергия поля) даются формулами:

где s = 1,2  компоненты векторов в плоскости, перпендикулярной волновому вектору (2 поляризации). Функция Гамильтона распадается на сумму независимых членов, каждый из которых соответствует бегущей волне с определенным волновым вектором и поляризацией и имеет вид функции Гамильтона одномерного гармонического осциллятора. Для перехода к квантовому описанию канонические переменные заменяются на операторы.

координат Q и обобщенных импульсов P ) соответствующими операторами. Собственные

значения гамильтониана находятся аналогично энергиям линейных осцилляторов (в системе единиц, где скорость света и постоянная Планка равны 1) .

Линейные комбинации операторов обобщенных координат Q и обобщенных импульсов P, соответствующие коэффициентам с в разложении векторного потенциала А имеют более глубокий смысл

В этом шредингеровском представлении операторы не содержат явной зависимости от времени, временнáя эволюция системы описывается временнóй эволюцией волновой функции. В гейзенберговском представлении явная зависимость от времени перенесена с волновой функции на операторы. В релятивистской квантовой теории равноправная зависимость операторов от координаты и времени позволяет более явно выявить релятивистскую пространственно-временную инвариантность теории.
В гейзенберговском представлении для операторов А в каждом члене суммы добавляется множитель exp(–iwt) (или ему сопряженный), соответствующий временнóй зависимости “стационарных состояний осцилляторов поля”

единственные отличные от нуля матричные элементы

е(s) – единичные вектора поляризации осцилляторов

величин в представлениях Шредингера и Гейзенберга (Н)
Изменение со временем волновой функции

в представлении Шредингера

Уравнения для операторов в представлении Гейзенберга

Изменение со временем плотности вероятности в представлении Шредингера

Волновая функция в представлении Гейзенберга (Н) не зависит от времени

Операторы в представлении Гейзенберга зависят от времени t:

Изменение со временем средних значений физических величин в представлениях Шредингера и Гейзенберга (Н)

вычеркнув энергию нулевых колебаний (слагаемое ½), вместе с импульсом поля

P они даются формулами (в обычных единицах).

Эти формулы служат обоснованием понятия о фотонах. Свободное электромагнитное поле можно рассматривать как совокупность частиц, каждая из которых имеет энергию и импульс Соотношение между импульсом и энергией – такое же как в релятивистской механике для частиц с нулевой массой покоя, движущихся со скоростью света. Числа Nks имеют смысл чисел фотонов с заданными импульсами и поляризациями. Свойство поляризации фотона аналогично понятию спина у других частиц. В методе вторичного квантования роль независимых переменных играют числа заполнения (в данном случае – числа Nks), а операторы действуют на функции этих чисел. При этом основную роль играют операторы “уничтожения” (с) и “рождения” (с+) фотонов, соответственно уменьшающие и увеличивающие на единицу числа заполнения. .

Плоские волны  коэффициенты перед операторами уничтожения фотонов можно трактовать как волновые функции фотонов с определенными импульсами и поляризациями, нормированные на “один фотон в объеме W”. Но волновую функцию фотона нельзя рассматривать как амплитуду его пространственной локализации. О координатах фотона имеет смысл говорить, когда характеристические размеры задачи велики по сравнению с длиной волны (“классический” предельный случай геометрической оптики). В квантовом случае, когда длна волны не может рассматриваться как малая, понятие координат фотона становится беспредметным.

правила коммутации для бозонов

(с тремя компонентами, при поворотах системы координат, преобразующиеся по определенному

закону) фотону можно приписать спин s = 1 (2s+1=3). Полный момент фотона складывается из спина (собственного момента) фотона и орбитального момента,
связанного с координатной зависимостью волновых функций. Состояниям с орбитальным моментом l соответствуют волновые функции, выражающиеся через сферические гармоники порядка l. Полный момент может пробегать лишь целочисленные значения: 1, 2, 3,… Состояние фотона может характеризоваться также его четностью, связанной с поведением волновой функции при инверсии системы координат. Состояние называют четным, если векторная волновая функция А(r) не меняет знак при инверсии, и нечетным, если она меняет знак. Принята определенная терминология для различных состояний фотона с определенными моментами и четностями: фотон в состоянии с моментом j и четностью (1)j называется электрическим 2j –польным (или Ej-фотоном), а при четности (1)j+1  магнитным 2j –польным (или Мj-фотоном),
Фотон с определенным направлением волнового вектора может иметь определенное значение проекции момента на это направление  спиральности. Спиральность совпадает с проекцией спина частицы на направление ее движения. Для фотона возможны лишь значения ±1.

правило, рассматриваться с помощью теории возмущений. Слабость электромагнитного взаимодействия выражается в

малости “константы связи” – постоянной тонкой структуры a = 1/137.
В первом приближении теории возмущений вероятности процессов определяются квадратом модуля |Vij|2 матричного элемента оператора возмущения между начальным (i) и конечным (j) состояниями системы зарядов и поля. Каждый из операторов “уничтожения” (с) и “рождения” (с+) фотонов имеет отличные от нуля матричные элементы лишь для уменьшения или увеличения соответствующего числа заполнения на 1. Поэтому и оператор A имеет матричные элементы лишь для переходов с однократным поглощением или излучением фотона.

Уравнение Дирака 1) для свободного движения электрона:

2) для электрона в электромагнитном поле с
калибровкой, в которой скалярный потенциал F = 0:

оператор взаимодействия с заданным электромагнитным полем оператор взаимодействия с изменяющимся электромагнитным полем

Здесь n – индекс состояния фотона. Для излучения или поглощения фотонов с определенными волновыми векторами и поляризациями, то волновые функции A – плоские волны. Если излучаются (поглощаются) фотоны с определенными значениями момента, то А – сферические волны.

if с испусканием фотона.
Для фотонов с определенными значениями волнового вектора.
С

учетом нормировки на 1 фотон в объеме W.

Матричные элементы
1) для испускания фотона

2) для поглощения фотона

Оператор взаимодействия с изменяющимся электромагнитным полем

Здесь Yi и Yf – волновые функции начального и конечного состояний излучателя (электрона). Один электрон и может излучать лишь при движении во внешнем поле. Свободный, движущийся с постоянной скоростью электрон не излучает.
Приведенные выше матричные элементы зависят от времени. Для перехода к независящим от времени матричным элементам выделяют в волновых функциях множители, зависящие от времени.

ток перехода

+ для поглощения фотона,  для испускания фотона

Дельта-функция выражает закон сохранения энергии, интегрирование по dw устраняет ее и приводит к выражению для вероятности испускания фотона в телесном угле do.

ток перехода в импульсном представлении

I определяется матричным элементом дипольного момента


Рассеяние света Рассеяние фотона атомом

представляет собой поглощение начального фотона (с волновым вектором k) с одновременным испусканием другого фотона k’. При этом атом может остаться либо на начальном, либо на каком-то другом уровне энергии. В первом случае частота фотона не меняется, такое рассеяние называют релеевским или несмещенным. Во втором частота фотона меняется на величину w’ – w = Ei – Ef, где Ei, Ef – начальная и конечная энергии атома (молекулы), такое рассеяние называют комбинационным или смещенным.
Естественная ширина спектральных линий: Естественная форма спектральной линии – распределение фотонов по частотам, G/ – вероятность (в 1с) всех возможных процессов “распада” данного состояния.

аналогично классической формуле для интенсивности излучения In c частотой w = nw0 системой частиц, движущихся периодически с частотой w0. Согласно принципу соответствия Бора компонентам Фурье классических величин отвечают квантовые матричные элементы в квазиклассическом случае, (но для интенсивности дипольного излучения I и в общем квантовом случае). Электрическое дипольное излучение фотона с моментом 1 и отрицательной четностью играет наиболее важную роль в оптических спектрах атомов и для приводит к приближенным правилам отбора при L-S-связи: Sf = Si, Lf = Li + 1, Li – 1,

Взаимодействие атома с квантованным полем излучения

Соотношение между вероятностью испускания wrad и вероятностью поглощения wcup фотона при переходах между заданной парой уровней излучающей системы (например, атома)

элемент оператора электромагнитного взаимодействия 1) для испускания фотона при условии, что

в начальном состоянии фотонов нет (Nn=0)
2) для испускания фотона при условии, что в начальном состоянии уже имеется Nn фотонов
Матричный элемент оператора уничтожения фотона
Матричный элемент оператора электромагнитного взаимодействия
1) для поглощения одного имеющегося фотона
2) для поглощения одного фотона из Nn имеющихся.

вынужденное (индуцированное) излучение

Соотношение между вероятностью испускания wrad и вероятностью поглощения wcup фотона при переходах между заданной парой уровней излучающей системы (например, атома)

было впервые установлено в 1916 г. Эйнштейном, предсказавшим явление вынужденного испускания. Оно лежит в основе принципа действия лазера.

угле do
В случае длины волны фотона l=2p/k много большей по

сравнению с размерами излучающей системы а. Пример: длины волн видимого света от 400 до 700 нм, размер атома порядка 0.1 нм. Импульсом фотона можно пренебречь по сравнению с импульсами частиц системы.

Это приближение соответствует дипольному приближению в классической теории излучения.

Замена матричного элемента тока перехода на нерелятивистское выражение – матричный элемент оператора скорости по отношению к шредингеровским (нерелятивистским) волновым функциям.

Дипольный момент электрона (в его орбитальном движении)

Вероятность дипольного излучения (вектор поляризации e должен быть перпендикулярен волновому вектору k.

Полная вероятность испускания получается интегрированием по всем направлениям испускания фотона и суммированием по двум возможным независимым поляризациям.
Для линейной поляризации, интегрирование по do сводится к умножению на 4p, а суммирование по поляризациям – к умножению на 2. Полная вероятность испускания фотона в системе единиц, где с = 1,

Полная вероятность испускания фотона в обычной системе единиц.

Интенсивность излучения

Приближенный оператор взаимодействия и оператор напряженности электрического поля для излучения любой нерелятивистской системой частиц.

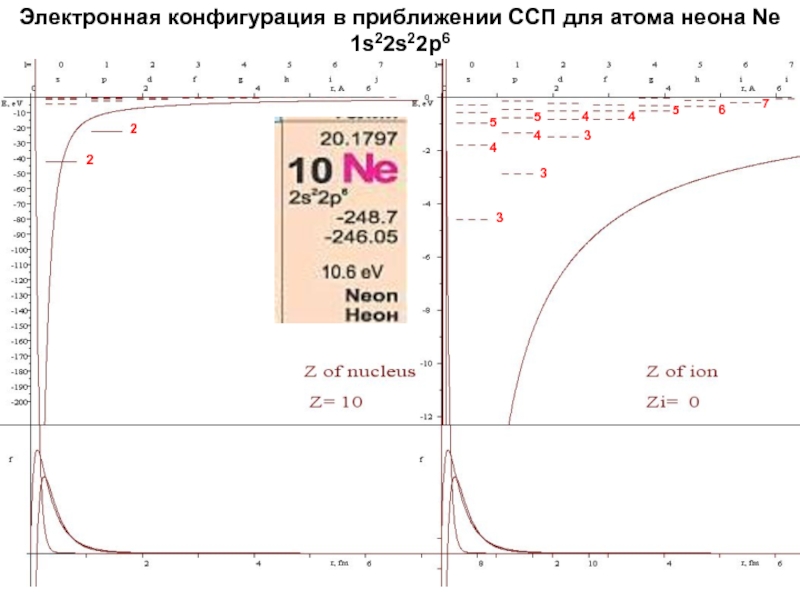
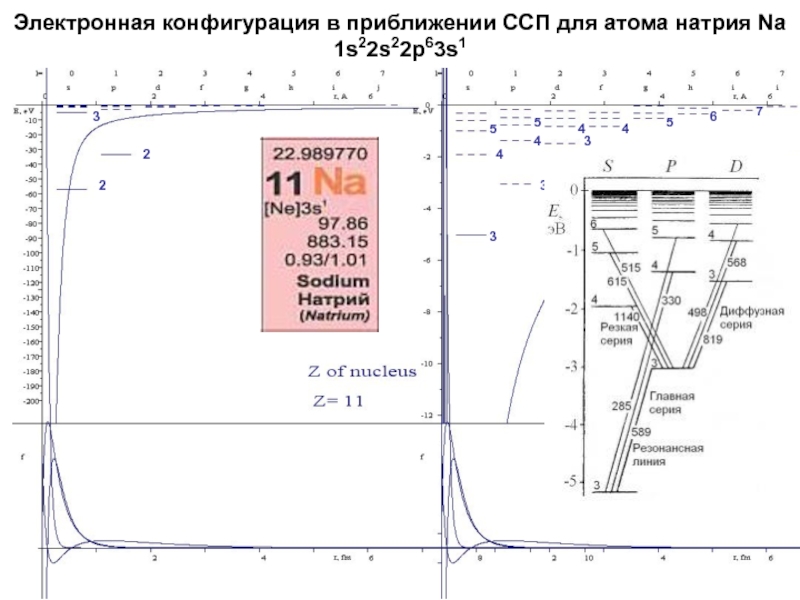
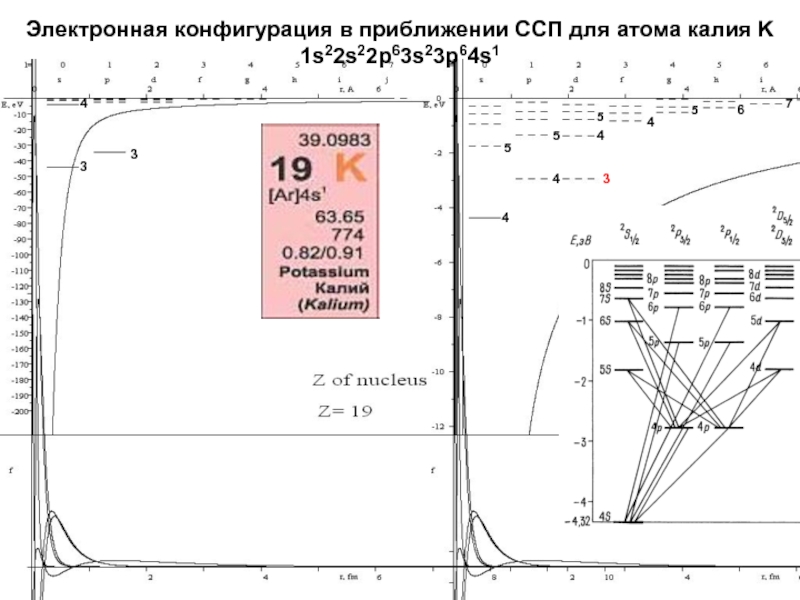
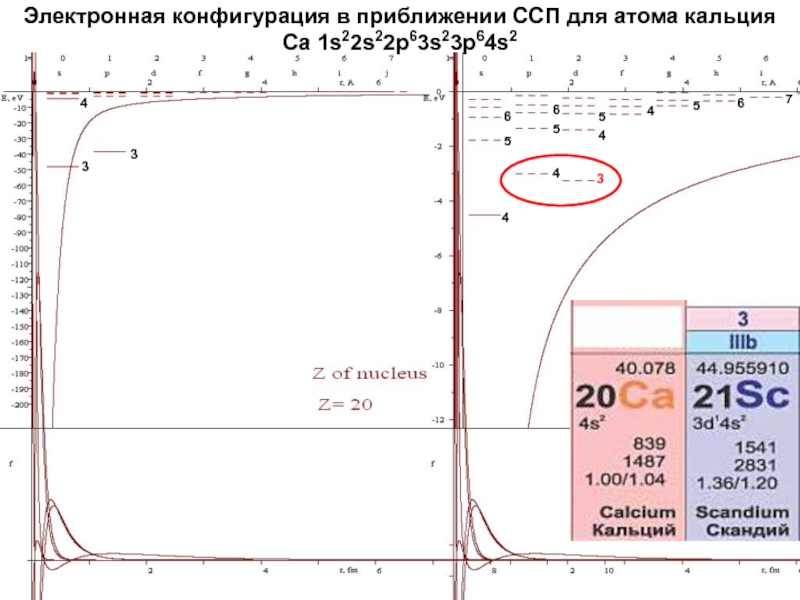
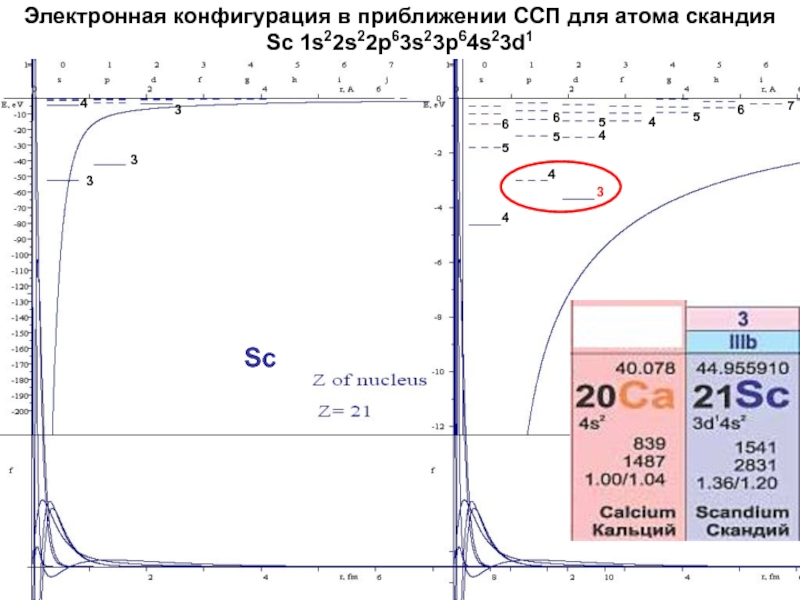
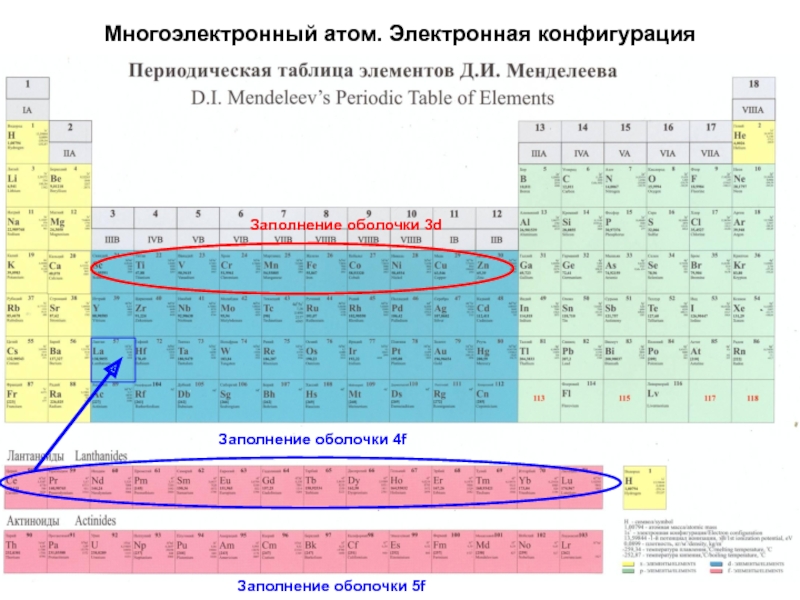
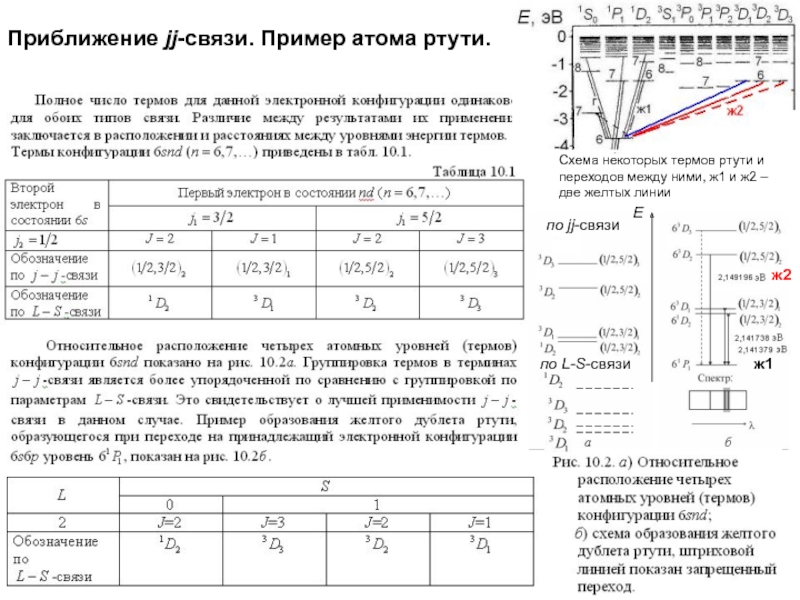
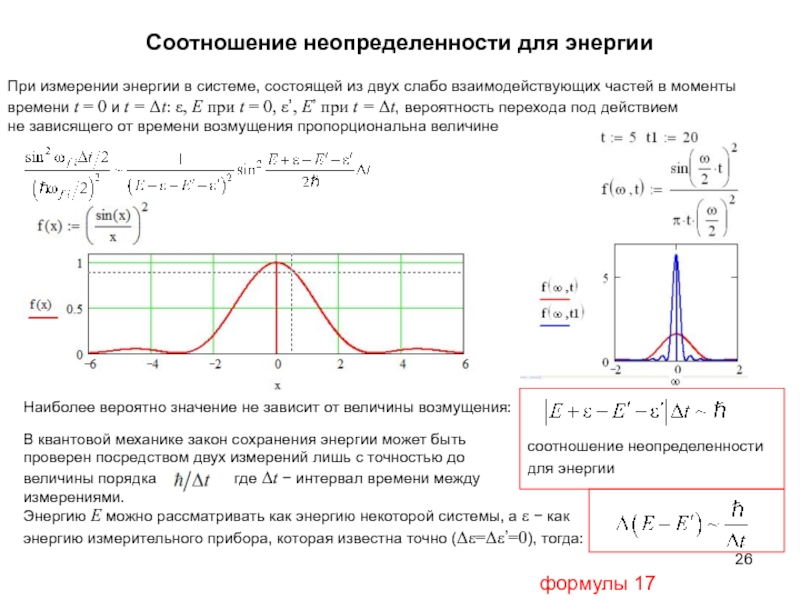
начальный момент излучающей системы Ji должен совпадать с суммарным моментом

конечной системы Jf и фотона j. Согласно квантовомеханическому правилу сложения моментов
Jf = Ji + j, Ji + j – 1, …| Ji – 1|, j = 1, 2,…

Начальная четность системы Pi должна совпадать с общей четностью конечной системы Pf и фотона Pg: Pi = Pf Pg. Поскольку все четности могут равняться только ±1, то PiPf = Pg. При любом значении j испускание одиночного фотона при переходе системы между двумя состояниями с J = 0 (переходы 00) запрещено правилом сложения моментов. При этом в более высоких приближениях теории возмущений возможно с существенно меньшей вероятностью одновременное испускание двух фотонов с антипараллельными моментами.
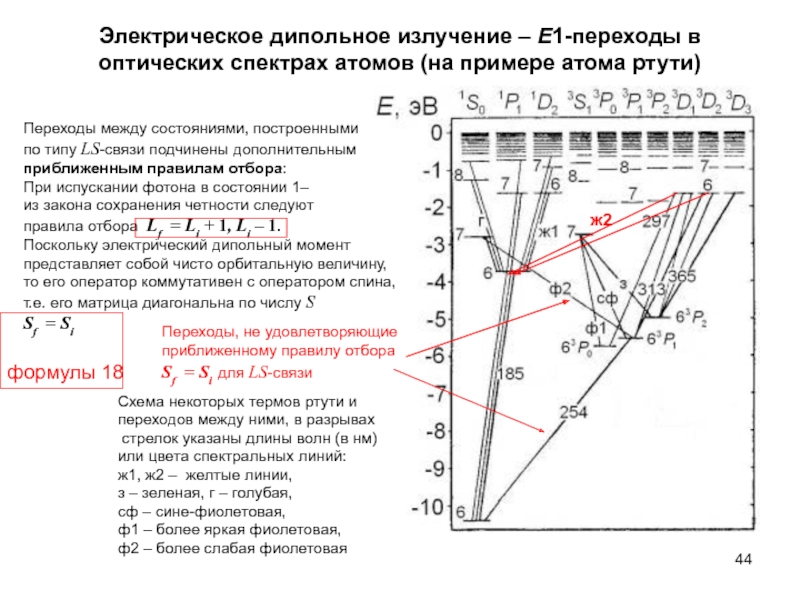
Дипольное приближение отвечает испусканию фотона в состоянии 1– (фотон Е1), при этом разрешены переходы между состояниями с противоположными четностями и со следующими возможными изменениями полного момента J: J  J + 1, J, J – 1 при (J  1), 0  1, ½  3/2, ½
В оптических спектрах атомов электрическое дипольное излучение – Е1-переходы наиболее важны, их вероятности (если они допускаются правилами отбора) значительно превосходят вероятности мульпольных переходов более высоких рангов.
Приближенные правила отбора для состояний, построенных по типу L-S-связи (при слабом спин-орбитальном взаимодействии, нарушающим раздельное сохранение орбитального момента и спина: Sf = Si, Lf = Li + 1, Li, Li – 1. Зависимость координатной волновой функции частицы от углов в центральном поле задается сферической функцией YLM, при инверсии она умножается на (–1)L. Поэтому все состояния с четным L четны, а с нечетным L нечетны. При испускании фотона в состоянии 1– из закона сохранения четности следуют правила отбора Lf = Li + 1, Li – 1.

Испускание фотона 1+ (фотон M1) называют магнитным дипольным излучением, фотона 2– –
электрическим квадрупольным излучением и т.д.

излучения
формулы 18

примере атома ртути)
Схема некоторых термов ртути и
переходов между

ними, в разрывах
стрелок указаны длины волн (в нм)
или цвета спектральных линий:
ж1, ж2 – желтые линии,
з – зеленая, г – голубая,
сф – сине-фиолетовая,
ф1 – более яркая фиолетовая,
ф2 – более слабая фиолетовая

Переходы между состояниями, построенными по типу LS-связи подчинены дополнительным приближенным правилам отбора: При испускании фотона в состоянии 1– из закона сохранения четности следуют правила отбора Lf = Li + 1, Li – 1. Поскольку электрический дипольный момент представляет собой чисто орбитальную величину, то его оператор коммутативен с оператором спина, т.е. его матрица диагональна по числу S
Sf = Si

Переходы, не удовлетворяющие приближенному правилу отбора Sf = Si для LS-связи

ж2

формулы 18

волновым вектором k) с одновременным испусканием другого фотона k’. При этом

атом может остаться либо на начальном, либо на каком-то другом уровне энергии. В первом случае частота фотона не меняется, такое рассеяние называют релеевским или несмещенным. Во втором частота фотона меняется на величину w’ – w = Ei – Ef, где Ei, Ef – начальная и конечная энергии атома (молекулы), такое рассеяние называют комбинационным или смещенным. Эффект рассеяния проявляется лишь во втором приближении теории возмущений. Его рассматривают как происходящее через промежуточные состояния двух типов: 1) Фотон k поглощается, атом переходит с начального уровня Ei на один из других своих возможных уровней En, при последующем переходе в конечное состояние испускается фотон k’. 2) Испускается фотон k’, атом переходит в состояние En, при переходе в конечное состояние поглощается фотон k. Такому описанию не следует придавать буквального смысла.
В первом порядке нестационарной теории возмущений матричный элемент Vfi и поправка к волновой функции равны нулю. Во втором порядке: В формулах первого порядка для сечения матричный элемент Vfi заменяется на сумму

Рассеяние света

Vni и Vfn  матричные элементы переходов с поглощением, а V’ni и V’fn  с испусканием фотона; из суммирования по n исключается начальное состояние атома (молекулы). Сечение рассеяния ds и амплитуда рассеяния Afi равны:

в системе единиц, где с = 1,

k  промежуточные состояния, далее обычные единицы

волновым вектором k) с одновременным испусканием другого фотона k’. При этом

атом может остаться либо на начальном, либо на каком-то другом уровне энергии. В первом случае частота фотона не меняется, такое рассеяние называют релеевским или несмещенным. Во втором частота фотона меняется на величину w’ – w = Ei – Ef, где Ei, Ef – начальная и конечная энергии атома (молекулы), такое рассеяние называют комбинационным или смещенным.

Рассеяние света

Сечение рассеяния ds и амплитуда рассеяния Afi равны:

Амплитуда рассеяния отлична от нуля только для переходов между состояниями одинаковой четности. При w  0 амплитуда рассеяния стремится к конечному пределу. Сечение несмещенного рассеяния (w’ = w) при малых w оказывается пропорциональным w4. При рассмотрении рассеяния света совокупностью N одинаковых атомов в объеме, размеры которого малы по сравнению с длиной волны, амплитуда рассеяния равна сумме амплитуд рассеяния на каждом из атомов. Волновые функции атомов определены с точностью до фазовых множителей, сечение рассеяния должно быть усреднено по ним независимо. Для смещенного рассеяния при усреднении по фазам атомов останутся лишь квадраты модулей каждого слагаемого. Полное сечение рассеяния N атомами получится умножением на N сечения рассеяния на отдельном атоме  складываются сечения рассеяния, а не его амплитуды. Такое рассеяние называют некогерентным. Если начальное и конечное состояния атома совпадают, то амплитуда рассеяния будет отличаться от амплитуды рассеяния на отдельном атоме множителем N, сечение рассеяния  соответственно множителем N2. Такое рассеяние называют когерентным.

Квантовая механика. − М. Наука. 1971.
Ландау Л.Д. Лифшиц Е.М. Курс

теоретической физики. Т. 3. Квантовая механика. Нерелятивистская теория − М. Наука. 1971.
Берестецкий В.Б., Лифшиц Е.М., Питаевский Л.П. Квантовая электродинамика. Ландау Л.Д. Лифшиц Е.М. Курс теоретической физики. Т. 4. − М. Наука. 1971.
Сивухин, Д. В. Общий курс физики. В 5 Т. Т 5: Атомная и ядерная физика: учеб. пособие– М.: Физматлит, 2002
Робертсон, Б. Современная физика в прикладных науках / Б. Робертсон. – М.: Мир, 1985.  272 с.
Хабердитцл, В. Строение материи и химическая связь. /В. Хабердитцл. – М.: Мир, 1974. – 296 с.